WGS-84坐标系下空基多平台异质传感器MLR配准*



WGS-84坐标系下空基多平台异质传感器MLR配准*

吴卫华，江晶

(空军预警学院，湖北 武汉430019)

摘要：多平台多传感器良好协同的重要前提之一是其系统误差的配准，由于空中平台的运动和传感器类型的异质性使得配准问题更为复杂。首先构建了WGS-84坐标系下有偏观测模型，然后将最大似然配准(maximum likelihood registration, MLR)算法扩展到空基多运动平台异质传感器的配准。运用复合函数求导链式法则，推导出应用MLR算法时至为关键的传感器观测量对目标状态的雅克比矩阵。理论和仿真结果表明该方法可实现异质传感器配准，配准误差逼近其Cramer-Rao界。

关键词：异质传感器配准；最大似然配准；WGS-84；多运动平台

0引言

将已有的各自独立的传感器组网，可有效提高系统的整体性能：如稳健性、覆盖范围、探测跟踪精度等，相比研发全新的装备，无疑是一种更为经济高效的方式[1]。然而，受传感器系统偏差的影响，首先需要解决传感器配准问题，否则，不但可能起不到提升性能的作用，甚至将造成性能的恶化，如对同一个目标可能在统一态势图上产生多条虚假航迹的“鬼影”(ghost)[2]。

为实现传感器的配准，主要有2类算法：一是为了达到实时性而提出的在线配准递归算法[3]；另一类是离线模式下的批处理算法。后者主要应用于传感器偏差在短时间变化缓慢的情况，其可进一步细分为最小二乘配准(least square registration, LSR)[4-5]和最大似然配准(maximum likelihood registration, MLR)[6-10]算法。LSR一般适用于同类传感器之间的两两相对配准，而MLR可用于任意数目的异质传感器之间的绝对配准，同时可对未知目标进行跟踪。

最初，MLR是基于二维区域性平面的球面投影(stereographic projection)[8-9]，随后，为在大范围监视区域精确的配准，文献[10]利用了从本地传感器量测到WGS-84坐标系的高精度大地坐标变换，提出了基于WGS-84坐标系的最大似然配准(WGS-84-MLR)算法(文献[10]的ECEF即为本文的WGS-84坐标系)。不过，上述文献主要是针对地面固定多站，文献[11]应用该算法对空基多运动平台进行了研究，但没有考虑姿态信息。为更贴近于WGS-84坐标系下的空基多运动平台，本文考虑平台不断变化的位置和姿态，研究了空基多平台多异质传感器的最大似然配准问题。

1WGS-84坐标系下有偏观测模型

设目标在WGS-84坐标系下的位置为Xk=(xk,yk,zk)T，则根据WGS-84坐标系到载机NED坐标系[12](该坐标系原点在载机质心处，地理北、东分别为x，y轴，z轴与x，y轴成右手系朝下)的坐标变换公式，可得目标在平台n的NED坐标系下的坐标为

(1)

式中：

(2)

式中：

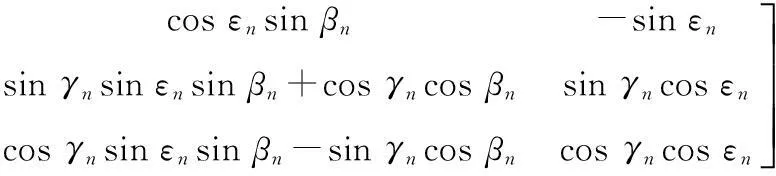
式中，为使式子简明，省略了表示时间索引的下标k。

当平台配置的传感器为有源类型时，观测集为斜距rk,n,方位ak,n(相对于机头，向右为正)和俯仰角ek,n：

zk,n=(rk,n,ak,n，ek,n)T.

当平台配置的传感器为无源传感器时，此时无斜距信息，观测集为方位和俯仰角：

zk,n=(ak,n，ek,n)T，

式中：

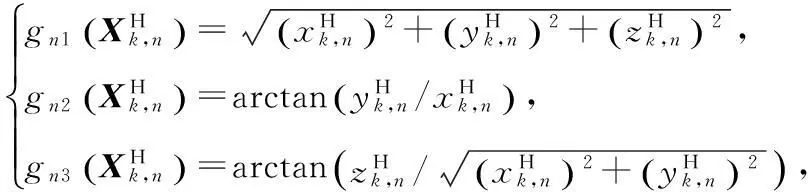
将上式写成矢量紧凑形式有

(3)

将式(1)和式(2)代入式(3)，从而可得观测与目标状态的非线性函数关系为

(4)

式中：待估计的状态为Xk∈p；是已知的非线性矢量量测函数。假定配准参数矢量bn为时不变确定量，并与Xk独立；wk,n为零均值白高斯噪声，协方差矩阵为∑zn；并且噪声序列wk,n在平台间相互独立，且有zk,n,hn,bn,wk,n∈qn。

2最大似然配准(MLR)算法

将N个传感器的观测矢量合并成一列，则有

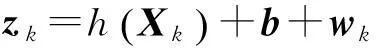
(5)

式中：

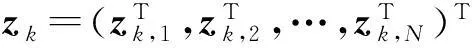
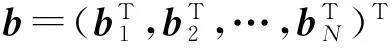
(6)

2.1目标状态估计

根据式(5)，可得目标状态与观测量有如下非线性关系：

式中：wk,n反映了上述映射是随机的。

那么，可将传感器n的观测量按下式(7)投影到目标状态空间

(7)

(8)

(9)

k时刻目标状态的最大似然估计(maximum likelihood estimate, MLE)[9]为

(10)

由式(7)可知，该估计依赖于未知的偏差矢量bn，它将由下节的算法进行估计。

2.2传感器偏差估计

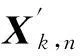
式中：雅克比矩阵Hk,n(qn×p维)由式(9)定义，上标-L表示左逆。该式用于迭代计算传感器偏差b。

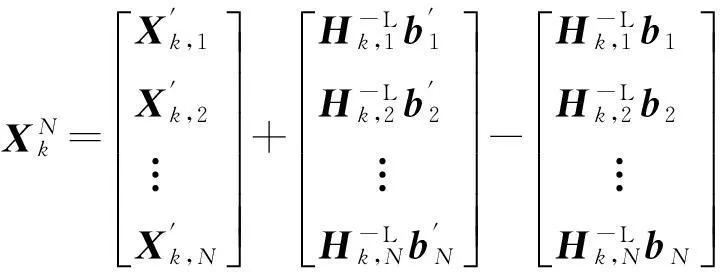
或者写成更紧凑的形式：

(12)

(13)

(14)

b的MLE为[9]

(15)

式中：

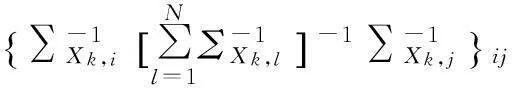
(16)

blkdiag(·)为Matlab函数，实现将输入子矩阵构造成对角块矩阵功能。式中的{·}ij表示尺寸为p×p的子矩阵所在位置为(ij)，其中，i,j=1,2,…，N。

2.3MLR算法执行

2.4Cramer-Rao界

假设b是需要估计的，而Xk是已知的，可以得到MLR算法较保守(低于实际值)的CRLB[9]

(17)

3MLR算法应用于WGS-84坐标系空基多运动平台异质传感器

由MLR算法过程可知，该算法至为关键的式子为Hk,n。为了将该算法应用于WGS-84坐标系下的空基多运动平台，需要求出观测量对目标状态的雅克比矩阵。

当传感器为有源类型时：

进一步化简可得

(18)

式中：

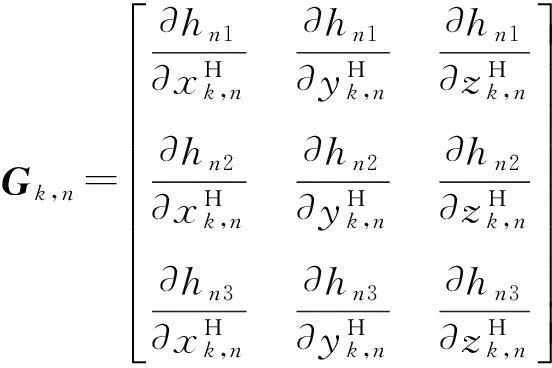
(19)

当传感器为无源类型时：

(20)

此时，

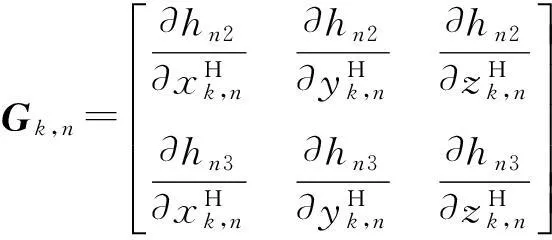
(21)

式中：

得到Hk,n后，即可根据MLR算法对空基多平台的传感器偏差进行配准。

4仿真分析

考虑2个(N=2)机载平台对同一未知运动目标的配准，假设两平台均做匀速直线运动，平台1的初始经纬高为119° E，24°N，8 000 m，初始速度为(100，-200，0)Tm/s，平台2的初始经纬高为119° E，26°N，8 000 m，初始速度为(100，200，0)Tm/s。目标的初始经纬高为121° E，25°N，3 000 m，按如下方程运动：

图1给出了算法的一次运行仿真结果(K=160)。从图1可知，从初始值b=05×1开始迭代，仅需3次迭代，各项偏差均可达到收敛。图2可看出配准补偿后的斜距、方位和俯仰角与真实值非常接近。

图1　不同迭代次数下各平台的传感器偏差估计结果Fig.1　Each sensor’s biases estimation during iteration process

图2　平台1和平台2的传感器配准前后观测与其真实值比较Fig.2　Unregistered and registered measurements (sensor 1 and 2) versus true values

图3　各平台传感器偏差估计误差均值Fig.3　Mean of sensor bias estimation errors

图4　各平台偏差估计误差标准差与CRLB比较Fig.4　Comparison of standard deviation of sensor bias estimation error and CRLB

5结束语

本文给出了应用于WGS-84坐标系下空基多平台异质传感器的MLR配准算法。仿真结果表明，该算法对空基异质传感器偏差是渐进无偏的有效估计量。下一步将对WGS-84坐标系下空基多运动平台的无源传感器配准问题展开研究，以及实现空基平台姿态偏差的配准。

参考文献：

[1]Dela Cruz E J, Ali T Alouani, Theodore R Rice,et al. Sensor Registration in Multisensor systems [C]∥Proceeding of the SPIE Symposium on Aerospace Sensing(Conference on Signal and Data Processing of Small Targets), Orlando, SPIE, 1992, 382-393.

[2]Gregory A Watson, Theodore R Rice. Sensor Alignment and compensation for Composite tracking [C]∥ Signal and Data Processing of Small Targets, Orlando, SPIE, 2002：354-367.

[3]连峰, 韩崇昭, 彭一峰, 等. 基于广义似然比的自适应在线配准算法 [J]. 控制与决策, 2009,24(1) : 23-28.

LIAN Feng,HAN Chong-zhao,PENG Yi-feng, et al. Adaptive on-Line Registration Algorithm based on GLR [J]. Control and Decision, 2009,24(1) : 23-28.

[4]ZHOU Yi-feng; LEUNG H, BLANCHETTE M. Sensor Alignment with Earth-Centered Earth-Fixed (ECEF) Coordinate System [J]. IEEE Transactions on Aerospace and Electronic Systems, 1999,35(2) : 410-418.

[5]Stefano Fortunati, Alfonso Farina, Fulvio Gini, et al. Least Squares Estimation and Cramer-Rao Type Lower Bounds for Relative Sensor Registration Process [J]. IEEE Transactions on Signal Processing, 2011,59(3) : 1075-1087.

[6]ZHOU Yi-feng; LEUNG H， YIP P C. An Exact Maximum Likelihood Registration Algorithm for Data Fusion [J]. IEEE Transactions on Signal Processing, 1997,45(6) : 1560-1573.

[7]Hwa-Tung Ong. Sensor Registration Using Airlanes: Maximum Likelihood Solution [C]∥ Signal and Data Processing of Small Targets 2003, Orlando: SPIE, 2003：390-401.

[8]MCMICHAEL D, OKELLO N. Maximum Likelihood Registration of Dissimilar Sensors [C]∥ Proceedings of the First Australian Data Fusion Symposium, Adelaide, Australia,1996：31-34.

[9]OKELLO N, RISTIC B. Maximum Likelihood Registration for Multiple Dissimilar Sensors [J]. IEEE Transactions on Aerospace and Electronic Systems, 2003,39(3) : 1074-1083.

[10]RISTIC B, OKELLO N. Sensor Registration in ECEF Coordinates Using the MLR Algorithm [C]∥ Proceedings of the 6th International Conference on Information Fusion (Fusion 2003), Cairns, Australia: ISIF, 2003：135-142.

[11]JIANG Jing, YUAN Jun-quan, MA Xiao-yan, et al. Divided Segment ML Registration for Multiple Moving Platforms Multiple Dissimilar Sensors [C]∥ Radar, 2006. CIE '06. International Conference on, 2006：1-5.

[12]江晶. 多运动平台多传感器信息融合技术应用研究[D]. 湖北武汉：武汉大学，2006.

JIANG Jing. Study on Multiple Moving Platforms Multiple Sensors Information Fusion Application [D]. Wuhan: Wuhan University, 2006.

MLR Registration for Dissimilar Sensors of Multiple Airborne Platforms in WGS-84

WU Wei-hua, JIANG Jing

(Air Force Early Warning Academy, Hubei Wuhan 430019, China)

Abstract:It is a precondition of coordinated operation for multi-platforms and multi-sensors to register these sensors, the registration problem will become more complex owing to airborne platforms’ motion and dissimilar sensors. Firstly, the biased measurement model based on WGS-84 (world geodetic system-84) coordinate system is constructed, and then the maximum likelihood registration (MLR) algorithm is extended to active sensor registration for multiple moving airborne platforms in WGS-84. By using the chain derivative rule of composite function, when MLR is applied, the key Jacobi matrix of sensor measurements to target state is derived. Theory analysis and simulation results show that the method can realize sensor registration, and the registration errors can approach the Cramer-Rao low bound.

Key words:dissimilar sensor registration; maximum likelihood registration (MLR); world geodetic system-84 (WGS-84); multiple airborne platforms

中图分类号：TN959.7; TP301.6

文献标志码：A

文章编号：1009-086X(2015)-02-0130-07

doi:10.3969/j.issn.1009-086x.2015.02.021

通信地址：430019湖北省武汉市江岸区黄浦大街288号931信箱E-mail： weihuawu1987@163.com

作者简介：吴卫华(1987-)，男, 湖南邵阳人。博士生, 研究方向为多源信息融合。

基金项目：国家自然科学基金项目(61102168)

* 收稿日期：2014-03-21；
修回日期：2014-06-28