球坐标系下多震相走时三参数同时反演成像
黄国娇, 白超英, 钱卫
1 河海大学地球科学与工程学院地质科学与工程系, 南京 211100 2 长安大学地质工程与测绘学院地球物理系, 西安 710054
球坐标系下多震相走时三参数同时反演成像
黄国娇1, 白超英2, 钱卫1
1 河海大学地球科学与工程学院地质科学与工程系, 南京 211100 2 长安大学地质工程与测绘学院地球物理系, 西安 710054
球坐标系下多震相走时三参数(速度、震源位置和反射界面)同时反演需要解决两个关键问题:(1)球坐标系下3D速度模型中多次透射、反射(折射)及转换波精确、快速的射线追踪;(2)同时反演时三种不同参数间的强耦合问题.为此,我们将直角坐标系下分区多步不规则最短路径算法推广至球坐标系中,进行区域或者全球尺度的多震相射线追踪.然后将其与适合多参数同时反演的子空间算法相结合,形成一种球坐标系下联合多震相走时三参数同时反演的方法技术.与双参数(速度和反射界面或速度和震源位置)同时反演的数值模拟对比分析显示:三参数与双参数的同时反演结果大体接近,并且它们对到时数据中可容许的随机噪声不太敏感.结果说明本文中的同时反演成像为一种提高成像分辨率,同时反演速度、震源位置和反射界面的有效方法.
球坐标系; 分区多步不规则最短路径算法; 多震相走时; 三参数同时反演; 子空间法
1 引言
自1976年Aki和Lee将医学层析成像技术应用于地震层析成像研究以来,地震层析成像技术经过近40年的不断发展和完善,已成为研究地球内部结构、以及介质各向异性行之有效的方法技术之一.其成像尺度涵盖范围很广,小到岩石组分,大至全球构造.对于区域或全球层析成像而言,地球曲率不可忽略,地球表面不能简单视作平面来处理(Snoke and Lahr, 2001), 而必须采用球坐标系才能保证所需的计算精度.同时,地球内部的结构是复杂变化的,需用三维球坐标系下的速度模型来描述.在速度异常(-2%)的南太平洋地区,Zhao和 Lei (2004)分别采用3D速度模型和1D速度模型计算走时和射线路径,结果显示PcP震相的射线路径改变了77 km,其他震相的射线路径偏差也达到了几十千米,走时也存在数秒的差异.因此,如果所研究区域达到一定的尺度时(例如区域、特别是全球走时成像),不考虑地球曲率的影响和介质的横向非均匀性,计算的射线路径和走时就会包含较大的误差.
目前应用较广的走时层析成像,高频假设等因素的制约导致其成像的空间分辨率较低.因此,在现有地震和地震台网分布情况下,采用多震相走时成像是提高分辨率非常有效的途径.多震相走时成像较为典型的一个例子是Zhao等(2005)利用美国Landers地震余震进行多震相(S,SmS,sSmS)走时同时反演S波速度和Moho面,其中仅采用相距200 km的两个观测台站和其间发生的180个余震,其结果表明使用多震相走时成像其空间分辨率可提高至台站间距的1/8~1/6(即25~35 km).
在多震相走时成像中,由于反射或反射转换波震相的走时由震源参数、3D速度分布和反射界面共同决定,且这三类参数反演前往往是未知的,并存在强耦合关系(如:震源位置较小的变化将引起射线路径、以及射线入射到界面上反射点位置的较大变化,反过来说,反射点位置较小的变化也将同样引起射线路径的变化等),因此要求反演算法应具有同时反演三参数(速度、震源参数、反射界面)的能力.
对于区域或者全球走时层析成像,为保证计算精度和提高成像分辨率,需要进行三维球坐标系下多震相走时三参数同时反演成像.由于全球走时成像中需要成千上万的走时数据(大多采用不仅仅是单一震相的走时),且缺少高效和高精度的三维正演射线追踪计算方法及相应软件,故目前采用较多的还是基于1D球坐标系下的两点射线追踪算法,此算法反演中假设射线路径不变,然后采用扰动的方法更新速度模型(Van der Hilst et al., 1997; Su et al., 1994; Grand et al., 1997).近些年来人们已意识到采用三维球坐标系的重要性,相继出现了几种不同的射线追踪方法,例如:Bijwaard和Spakman(1999)研发的快速运动学射线追踪算法,在网格算法中引入了弯曲法,能够追踪3D球坐标系下的(临界)折射、多次反射、以及一些绕射(Pdiff)波,且计算的各主要震相绝对走时误差约为0.1 s,但实质上该算法依然是两点间的射线追踪.Zhao和Lei (2004)将球坐标系下的伪弯曲射线追踪算法(Zhao et al., 1992)进行了推广,可进行区域或全球多震相走时反演成像.Tian等(2007)开发了一套可用于全球有限频成像的动力学射线追踪程序,所计算的主要震相走时绝对误差约为0.1 s,但其算法依然是基于两点间的射线追踪问题(局域解问题),计算速度仍然存在问题(每个震源和台站都需要重新进行射线追踪).
目前为止,走时三参数(速度、反射界面和震源参数)同时反演研究并不多见,Sambridge (1990)虽然是首位讨论走时三参数同时反演的研究学者,反演采用子空间反演方法(Kennett et al., 1988),但其正演采用了传统的边界值两点射线追踪算法(Sambridge and Kennett, 1990);Preston (2003)在他的博士论文中也进行了走时三参数同时反演的研究工作,其研究成果已在Science上发表(Preston et al.,2003),其中利用正则化加权处理方式对三种参数进行解耦,容易引入人为因素.在直角坐标系下,黄国娇和白超英(2013)采用分区多步最短路径算法(Multiple ISPM)进行多震相的射线追踪,反演采用子空间算法,实现了3D多震相走时三参数同时反演成像.
鉴于此,针对区域或全球层析成像,本文将上述分区多步最短路径算法推广至球坐标系中,进行多震相走时和射线路径的追踪计算.然后将其与地震多参数反演算法(子空间反演算法)相结合,提出了一种3D球坐标系下可利用地震多震相走时资料进行三参数同时反演的方法技术.为验证该三参数同时反演算法的有效性和正确性,我们选用一个区域模型进行数值模拟实验,在合成理论走时数据中加入随机噪声并对其进行三参数同时反演,将反演成像结果与双参数同时反演进行对比分析.结果表明,三参数和双参数同时反演方法技术具有相近的反演能力,都能较好地反演出震源位置、速度分布、界面形态和位置.
2 多震相射线追踪算法
2.1 参数化
利用分区多步不规则最短路径算法进行射线追踪之前,需要将模型参数化.三维球坐标系下模型参数化如图1所示,首先根据速度间断面的起伏形态将模型分为四个区(图1a),然后对每个区域用规则单元或者不规则单元将其参数化.地心点所在单元形成如图1c所示的五面体,图1d为两极极点所在单元,而不包含地心、极点且远离起伏地表和界面的区域则可采用如图1b所示的规则六面体单元参数化.单元的角点为主节点,主节点间等距离的插入次级节点(这点很重要,因为越往地心,相同扇形的单元弧长越短),次级节点只分布在网格单元的边上,单元内无节点,但震源和地震台站可以位于其中.
2.2 速度插值
速度采样在主节点上进行,次级节点的速度可由主节点上的速度值通过三次线性插值函数(3D)得到.当节点(震源或者地震台站)位于单元内部时,需分规则单元和非规则单元两种情况对待:
(1) 当节点位于规则单元中,如图1b所示,节点速度则由所在单元八个主节点上的速度值通过三线性拉格朗日插值函数给出,插值函数为:
(1)

(2) 若节点位于不规则单元内,如图1c—1d所示,则需先将单元剖分为几个四面体(四面体的四个角点必须是主节点,编号1—4),然后再由节点所在四面体的四个主节点上定义的四面体体积插值函数给出(Huang et al., 2013):
(2)
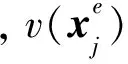
2.3 分区多步计算原理
图1 球坐标系下模型参数化示意图(图a, 为清晰起见, 次级节点未标出)和所用参数化单元(图b—d), 图b—d中大球表示主节点, 小球表示所加入的次级节点Fig.1 Model parametrization in 3D spherical coordinates (diagram a, for clear representation, the secondary nodes are not depicted) and three kinds of cells used to divide the spherical model (diagram b, c and d, in the figure the larger circles are primary nodes and the smaller circles are the secondary nodes, respectively)
分区多步计算首先是模型分区,然后按照给定的震相,自震源所在区域开始,沿着目标射线通过的区域分段分区进行射线追踪计算.举例来说,如图1a中所示,根据反射界面将模型分为了四个区,速度不连续(间断)面连接相邻区域.若计算图1a中界面一(深度660 km)的透射或反射震相时,首先自震源所在的单元开始波前扩展计算,然后按照一定的步长进行第一区的波前扩展计算.等第一区所有节点上的走时计算完成之后,波前停留在第一区的速度离散界面上,并保存了震源到界面离散点上的最小走时及相应的射线路径.此时如果计算透射波P1P2(上、下标分别代表上行波和下行波,1和2表示区号),则调用第二区的P波速度(如果追踪P1S2震相则调用第二区的S波速度),自界面一上走时最小的点开始进行第二区向下的波前扩展扫描计算;若是计算反射波P1P1(或反射转换波P1S1),同样自界面一上走时最小的点开始,并调用第一区相应的速度模型向上进行波前扩展计算.同理,依据多次波是由简单的入射、透射、反射及转换波按照一定的规律组合而成的原理,即可实现任意多震相地震射线的追踪计算.图2是3D球坐标系下采用上述分区多步不规则最短路径算法追踪计算的多震相射线路径图(所用速度模型和反射界面位置详见第4节反演实例),更复杂的多次波均可采用该算法进行追踪计算,但是需要在输入文件中给出多次波的传播途径,即射线穿过哪些区域,与哪些界面相交,遇到界面是反射、折射还是转换.
2.4 计算精度和效率分析
Huang等(2013)将该算法计算的49种不同的全球主要震相走时与AK135全球走时表(Kennet et al., 1995)进行对比分析,讨论该算法的计算精度问题.结果表明绝大多数震相的最大绝对走时误差小于0.1 s.在全球或者区域走时层析成像中,还要求正演算法具有较高的计算效率.因此,我们分析了图2所示模型中三种不同震相(P,P410P和P660P)在不同尺度单元参数化和次级节点情况下的计算效率,结果如图3所示.其中震源和台站的个数及位置分布均与第4节的反演实例中相同,单元大小分别为4°×4°×200 km(图3a)、2°×2°×100 km(图3b)和1°×1°×50 km(图3c),计算机配置为Intel i5-2300CPU处理器、2.8 GHz的主频和4 G内存.

图2 球坐标系下多震相射线路径图浅灰色线:初至P波;灰线:深度410 km处界面的反射波P410P;黑线:深度660 km处界面的反射波P660P.Fig.2 Multiple ray paths in a spherical coordinateThe directed arrivals (light grey lines), the reflection from the 410 km subsurface (gray lines) and the reflections from 660 km subsurface (black lines) are shown.
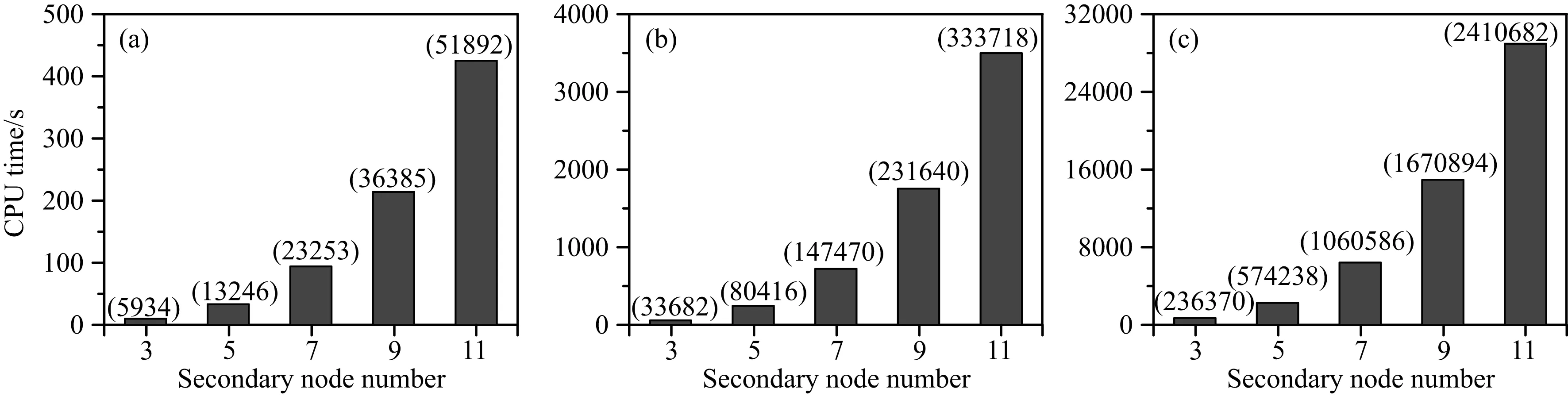
图3 计算多震相(P,P410P和P660P)的CPU时间图(a) 4°×4°×200 km;(b) 2°×2°×100 km;(c) 1°×1°×50 km.图中括号内数字为当前模型参数化下节点总数.Fig.3 Results of computational efficiency tests on tracing the multiple phases ( P, P410P and P660P)(a) Cell scale of 4°×4°×200 km; (b) Cell scale of 2°×2°×100 km; (c) Cell scale of 1°×1°×50 km. In the figures, the numbers in the parentheses indicate the total number of nodes for the corresponding parameterized model.
从图3c中可以看出,当单元大小为1°×1°×50 km,加入11个次级节点(地表次级节点间隔约为8 km)时,计算这三种震相几乎要花费近8个小时.但是,通常加入5~7个次级节点(次级节点间距为17~22.5 km)就能满足精度需求,此时CPU时间就减少至1.0~1.5个小时.值得注意的是,反演成像中每次迭代基本上有95%的时间花费在计算这三种震相的走时和射线路径上.因此,我们可大致估计采用上述三种震相同时反演三参数的时间.
3 反演算法
三参数的同时反演是一项很困难的工作,因为三者具有不同的物理量纲,并且具有强耦合关系.若在同一个方程中求解这三种不同的模型参数,解会偏向系数大的一方,很可能导致反演的失败.因此,如何解耦成为三参数同时反演中急需解决的问题.直角坐标系中,我们将共轭梯度法求解带约束的阻尼最小二乘算法(DMNCL-CG)和子空间法(Subspace)进行了对比,结果表明Subspace更适合于多参数的同时反演.因此,本文采用Subspace算法对球坐标系中三参数进行同时反演.
3.1 子空间算法(Subspace)
多震相走时同时反演可归结为求下列目标函数的极小值问题(Rawlinson and Sambridge, 2003):

(3)

子空间法是在模型的若干个子空间同时沿着多个方向去寻找目标函数S(m)的最小值.其算法的核心是将多种参数的模型扰动量用p维子空间的一组基向量{aj},j=1,2,…,p来表示,即
(4)
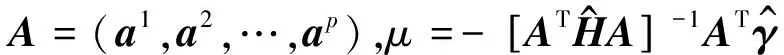
(5a)
(5b)
其中Frechet偏导数矩阵G=∂g/∂m.将表达式(5a)(5b)代入公式(4)中就可得到反演每次迭代时模型的更新量:
(6)
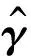
第二步:若p≥1,则采用下列公式构建其余的基向量:
⋮
第三步:采用奇异值分解法(SVD)将第一步和第二步中构建的基向量{aj}标准正交化.
3.2 Frechet偏导数计算
三维球坐标系中,地球内任一点P可表示为(r,θ,φ),实际应用中通常用径向深度、纬度和经度来表示,记为(z,Lat,Long),并且有r=R-z(R=6371.5 km为地球半径);θ=90°-Lat和φ=Long.根据射线理论,由第i个震源经反射点到达第j个检波器的走时可表述为下列积分:
(7)
其中ds为沿路径Rij上的线积分元,而Vc(r,θ,φ)则为沿射线路径上的速度分布函数.当模型网格单元化后,沿该射线路径Rij上的走时可写成求和形式:
(8)
其中:n为射线穿过的单元总数,Rij,k、Vc,k(r,θ,φ)分别为射线穿过第k个单元的长度和速度分布.
在速度、界面和震源位置同时反演时,Frechet偏导矩阵包含了三部分:一是走时关于速度变化的导数,二是走时关于反射点深度变化的导数,三是走时关于震源参数的导数.
(9)
其中vk和rk分别是第k个单元内的速度分布和第k个反射点的深度,Δvk和Δrk则分别是相应速度和反射点深度的扰动量,Δxk(k=1,2,3)是第k个震源分别在r,θ和φ方向的扰动量.
(9)式中第一项,即有关走时关于速度的一阶偏导数计算如下(为简便起见,这里略去震源编号i,则tj是第j条射线Rj的走时):

(10)
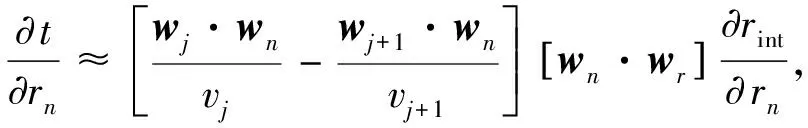
(11)
其中rn是离散界面节点的深度坐标,rint是反射点的深度坐标(有关wj,wj+1,wn和wr,见图4所示),球坐标系中wr=(1,0,0),∂rint/∂rn根据界面节点上的深度插值函数计算.vj和vj+1分别是界面两侧的速度值.当仅考虑反射时,wj+1·wn=-wj·wn和vj=vj+1,则(16)式简化为:
(12)
(9)式的第三项,即走时关于震源参数(位置和发震时刻)变化的偏导数可由以下步骤计算,首先走时(t=ta-to)关于发震时刻的导数为:
(13)
而走时关于震源深度变化的偏导数的计算可参见图5所示.假设震源的深度扰动值为Δrh,则走时关于震源深度变化的偏导数可表示为:
(14)
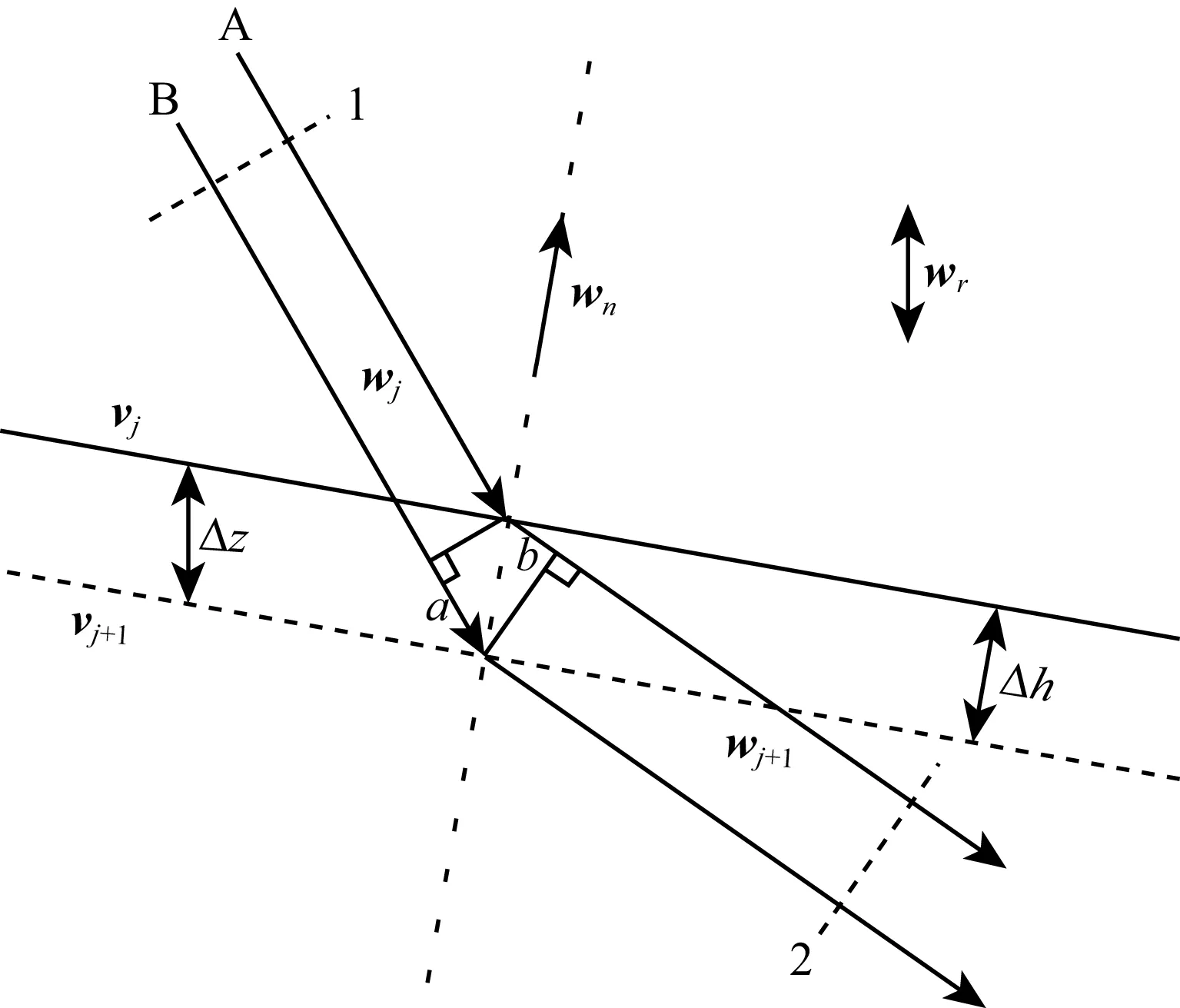
图4 走时关于反射点深度偏导数计算示意图Fig.4 Diagrammatic showing the calculation of traveltime derivative with respect to reflector depth change

图5 走时关于震源位置变化偏导数计算示意图Fig.5 Diagrammatic showing the calculation of traveltime derivative with respect to source location change
同理可得走时关于震源位置其余两个方向(Lat,Long)变化的偏导数表达式:
(15)
其中αh如图5所示,代表射线与r轴的夹角;βh和γh则是射线在θφ平面投影后分别与θ和φ轴的夹角.
4 数值模拟分析
为检验该三参数同时反演算法的有效性及正确性,我们选择一个尺度为20°×20°×700km的区域模型,如图6所示.图6a是经度-深度剖面的起伏速度图,速度沿着纬度方向不变化.模型中引入两个起伏反射界面模拟地幔中两个速度不连续面(如图6b所示),深度分别位于410km和660km处,起伏幅度均为±20km.模型参数化选用1°×1°×50km的单元,次级节点间距为10km(相当于在单元面的不同方向加了9个次级节点).30个震源随机分布在深度20km至100km之间(图7a是震源在经纬度面上的投影;图7b则是震源在经度-深度剖面上的投影),441个检波器均匀(间距为1°×1°)分布于地表(模型顶面).
本文的同时反演中采用了3种不同的震相:直达P波、反射界面410km和660km的一次反射波(P410P、P660P).为检验反演算法抗噪声能力,三种震相走时数据中加入了随机噪声(直达P波、P410P和P660P分别加入±0.2s、±0.3s和±0.3s的随机误差).选用背景层状速度作为初始速度模型,两个初始界面均为水平(深度分别为410km和660km).为了模拟实际地震定位中存在误差这一现实,初始震源位置的选择则是分别对实际震源位置在三个方向(经度、纬度、深度)进行扰动后得到,其相应扰动最大幅度分别为±2°、±2°和±10km.
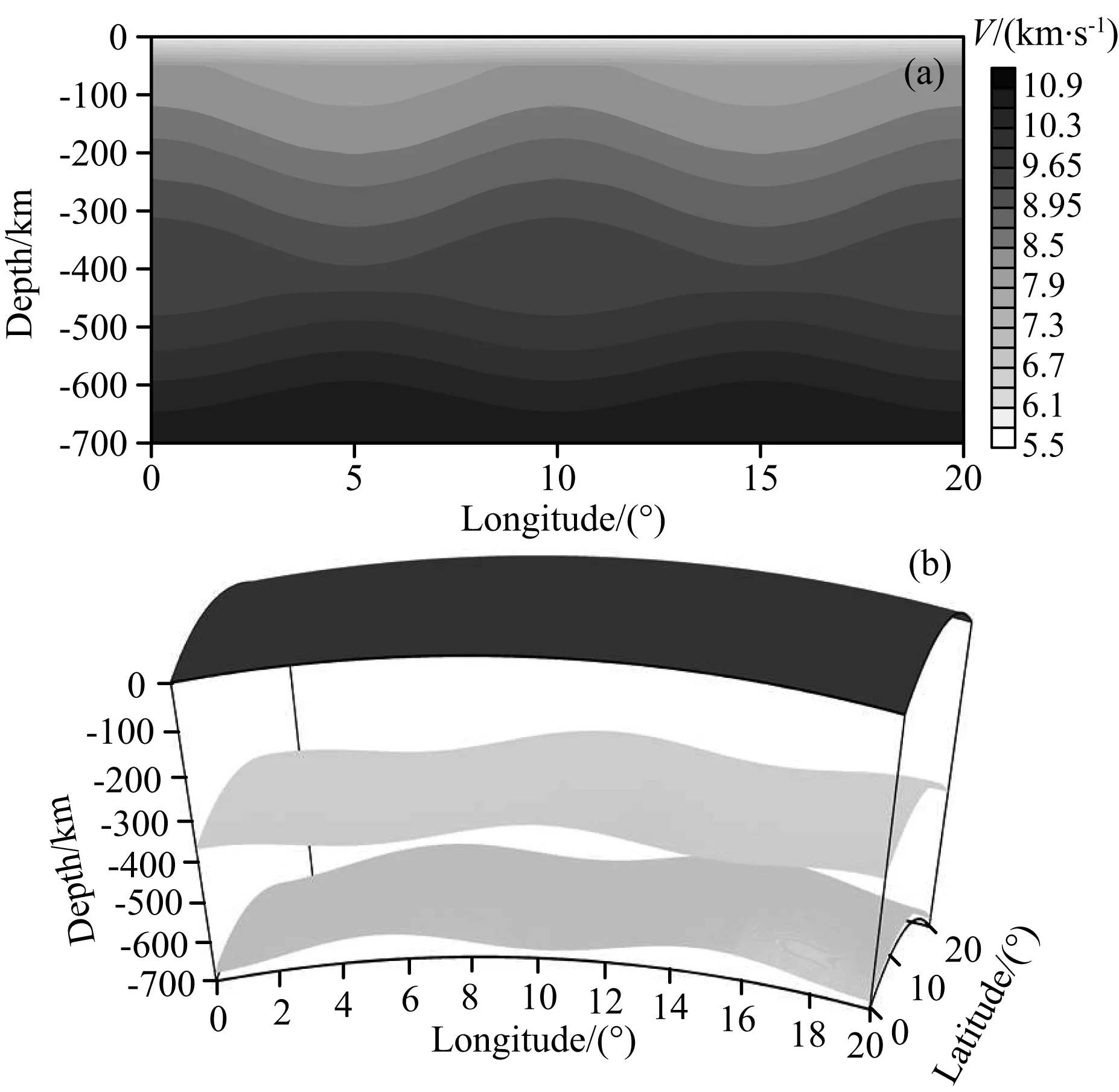
图6 (a)某一纬度时, 经度-深度剖面速度图; (b)两个起伏反射界面图Fig.6 (a) Velocity model showing one cross section and (b) two undulating subsurface interfaces
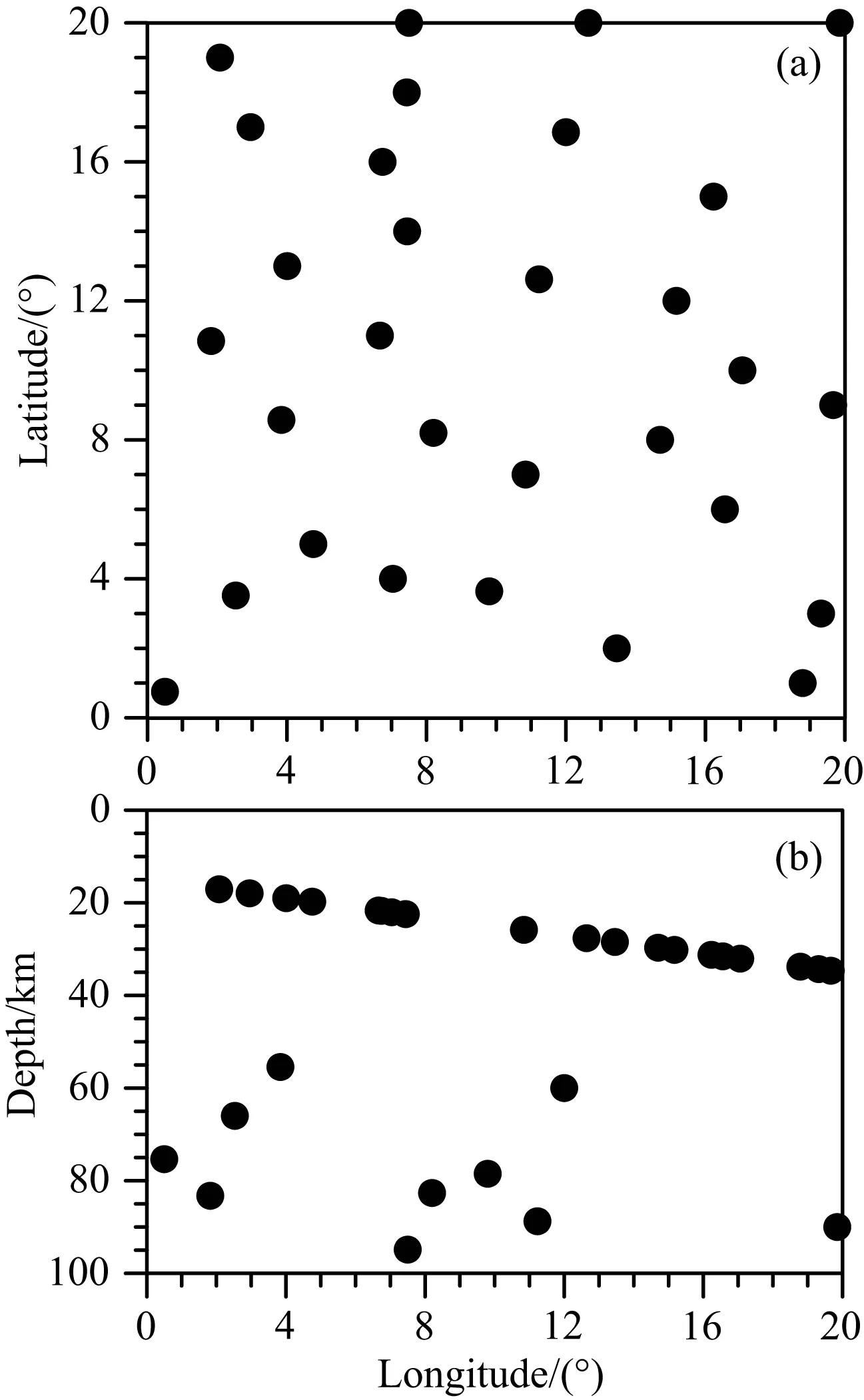
图7 震源在经纬度剖面(a)和经度-深度剖面(b)投影Fig.7 The sources projected on the horizontal plane (a) and the longitude-depth cross section (b)
为了进行系统的对比研究,模拟实验中进行了三种不同的反演,其一是速度和界面的同时反演(简记为:V+R反演),其二是速度和震源位置的同时反演(简记为:V+S反演),其三是速度、界面和震源位置的同时反演(简记为:V+R+S反演).不失一般性,三种不同的反演选用相同的反演参数,即阻尼因子和子空间维数分别为0.001和6(对2~8之间逐一尝试,选择较合适的子空间维数为6).迭代均为15次,相应的走时残差分别由初始时的1.834s,9.15s,9.269s下降至0.087s(V+R反演), 0.25s(V+S反演), 0.289s(V+R+S反演).
图8给出了三种不同反演算法在Lat=10°垂直剖面上速度场的反演结果.从中可以看出,三种不同的反演算法重建的速度场分布与真实速度(图8a)具有相似的异常形态,但是异常起伏的幅度似乎未完全恢复,且模型下部的更新相对较差,其主要原因是模型下部只有P660P震相的射线穿过,射线覆盖率和交叉概率有限所致.对比图8b—8d,会发现相对于双参数的反演结果(图8b和8c),三参数同时反演的结果(图8d)要略差些,但是差异不明显,仍然能够反演出异常的形态和结构.
为更加直观显示反演更新的速度场与真实速度场之间的差异,图9给出了与图8对应的垂直剖面上反演的速度场与真实速度场之间的百分比差异.从图9中可以看出,虽然三种反演方法都能重建出速度异常的形态和结构,但是速度异常幅度并未完全恢复.并且,可以明显地看出双参数同时反演结果要略好于三参数同时反演结果,特别是模型下部速度异常的重建结果.
图10为两种反演算法对反射界面的更新结果.可以看出,两种反演算法都能较好地更新反射界面的形态和位置,与真实反射界面(图6b)很相似,但仅从图10中无法判断哪种算法的更新结果更好.因此,为进一步评价反射界面的更新结果,我们给出了两种反演算法更新的反射界面与真实反射界面间的平均差异(表1).由于三参数(V+R+S)同时反演的难度远大于双参数(V+R)同时反演的难度,故从表1中可知,双参数(V+R)同时更新反射界面的结果要略好于三参数(V+R+S)同时更新的结果,但通过图10的对比可得出三参数也能较好地更新反射界面几何形态和位置.

图8 三种反演算法在Lat=10°垂直剖面的成像结果(a) 真实模型; (b) V+R; (c) V+S; (d) V+R+S.Fig.8 The reconstructed velocity fields in Lat=10 ° cross section with three kinds of inversion methods(a) Real velocity model; (b) V+R; (c) V+S; (d) V+R+S.
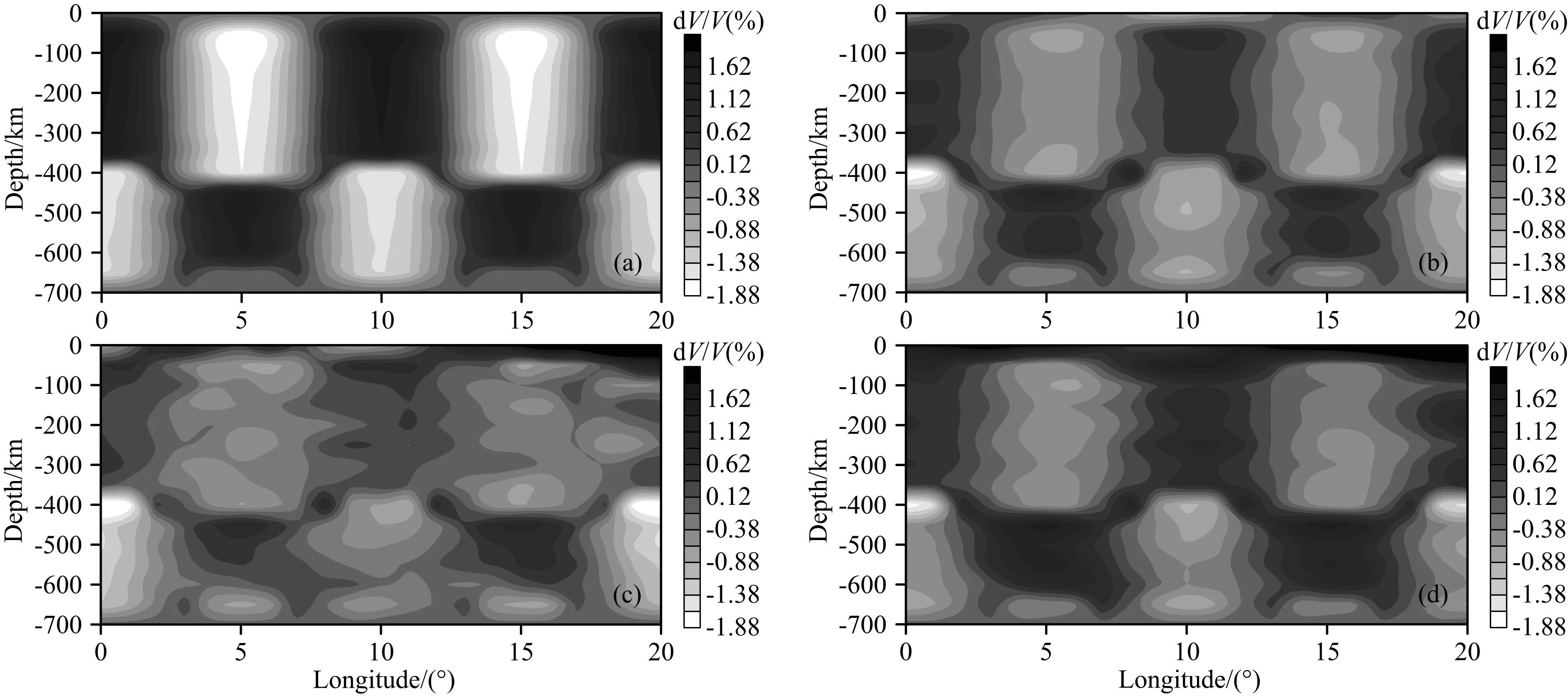
图9 三种不同反演算法的反演结果在Lat=10°垂直剖面上与真实速度的百分比误差(a)初始速度模型; (b) V+R反演结果; (c) V+S反演结果; (d) V+R+S反演结果.Fig.9 The difference (in percentage) between the initial and true velocity model in Lat=10° cross section, between the true velocity and the inverted velocity with three different inversion methods in the same cross section(a) Initial velocity model; (b) Results for the V+R inversion; (c) Results for the V+S inversion; (d) Results for the V+R+S inversion.

图10 两种不同反演算法更新的反射界面(a) V+R反演结果; (b) V+R+S反演结果.Fig.10 The updated reflected interfaces by the two different inversion algorithms(a) Results for the V+R inversion; (b) Results for the V+R+S inversion.

图11 两种不同反演算法得到震源的位置(a, d, g)、水平位置(b, e, h)和深度(c, f, i)分别相对于真实震源位置的收敛情况(a, b, c)初始值; (d, e, f) V+S反演结果; (g, h, i) V+R+S反演结果.DZ表示在深度方向上距离真实震源的距离.Fig.11 The convergence to the real source locations (a, d, g), the real horizontal position (b, e, h) and the real focus depths (c, f, i) by two different algorithms(a, b, c) Initial; (d, e, f) Results for the V+S inversion; (g, h, i) Results for the V+R+S inversion.

表1 界面深度平均绝对误差统计表Table 1 Mean absolute error statistics of the inverted depth for the two interfaces
图11是两种不同反演算法对震源位置的更新结果.这里我们用三种收敛情况来评价震源位置的更新结果,更新的震源位置相对于真实震源位置距离的收敛情况(图11左)、更新震源的水平位置相对于真实震源水平位置距离的收敛情况(图11中)和更新的震源深度相对于真实震源深度的收敛情况(图11右).从图11中可以看出,双参数的反演结果(图11d, 11e, 11f)要略好于三参数的反演结果(图11g, 11h, 11i).无论是双参数(V+S)的同时反演结果(图11d—11f),还是三参数(V+R+S)的同时反演结果(图11g—11i),其中对震源水平位置(图11e和11h)的更新结果均明显好于震源深度(图11f和11i)的结果.可知在该模型下存在震源深度的定位误差大于水平面内的定位误差的问题,其主要原因是对于区域或者全球成像而言,虽然利用了反射波走时资料,但模型尺度相对较大,走时对震源深度较小的变化不敏感,从而导致震源深度的更新相对较差.然而,在初始震源偏离真实震源较远(此例中最大距离约为320 km)的情况下,三参数的同时反演中,对震源的更新结果还是较为理想的.
5 结论
对于区域或全球层析成像,为保证计算精度、提高成像分辨率,本文将直角坐标系下的多震相射线追踪正演(Multistage ISPM)算法推广至球坐标系中,并与比较流行的多参数反演算法(Subspace)相结合,提出一种3D球坐标系中多震相走时三参数同时反演的方法技术.数值模拟实例表明,三参数同时反演方法技术和双参数反演方法具有相近的反演能力,都能较好地反演出震源位置、速度分布、界面形态和位置.另外,无论是双参数或是三参数同时反演算法均对走时数据中的随机误差不太敏感,这点在实际应用中也是至关重要的.因此,本文提出的球坐标系下的三参数同时反演算法是一种利用多震相走时资料同时反演速度、震源位置以及反射界面行之有效且实用性较强的方法技术.
Aki K, Lee W H K. 1976. Determination of three-dimensional velocity anomalies under a seismic array using first P arrival times from local earthquakes: 1. A homogeneous initial model.J.Geophys.Res., 81(23): 4381-4399.
Bai C-Y, Greenhalgh S. 2005. 3-D non-linear travel-time tomography: Imaging high contrast velocity anomalies.PureAppl.Geophys., 162(1): 2029-2049.
Bai C Y, Huang G J, Zhao R. 2010. 2-D/3-D irregular shortest-path ray tracing for multiple arrivals and its applications.Geophys.J.Int., 183(3): 1596-1612.
Bai C Y, Huang G J, Li Z S. 2011. Simultaneous inversion combining multiple-phase travel times within 3D complex layered media.ChineseJ.Geophys. (in Chinese), 54(1): 182-192, doi: 10.3969/j.issn.0001-5733.2011.01.019.
Bijwaard H, Spakman W. 1999. Fast kinematic ray tracing of first- and later-arriving global seismic phase.Geophys.J.Int., 139(2): 359-369.
De Kool M, Rawlinson N, Sambridge M. 2006. A practical grid-based method for tracking multiple refraction and reflection phases in three-dimensional heterogeneous media.Geophys.J.Int., 167(1): 253-270.
Grand S P, Van der Hilst R D, Widiyantoro S. 1997. Global seismic tomography: A snapshot of convection in the Earth.GSAToday, 7(4): 1-7.
Huang G J, Bai C Y. 2010. Simultaneous inversion with multiple traveltimes within 2-D complex layered media.ChineseJ.Geophys. (in Chinese), 53(12): 2972-2981, doi: 10.3969/j.issn.0001-5733.2010.12.021.
Huang G J, Bai C Y, Greenhalgh S. 2013. Fast and accurate global multiphase arrival tracking: the irregular shortest-path method in a 3-D spherical earth model.Geophys.J.Int., 194(3): 1878-1892.
Huang G J, Bai C Y. 2013. Simultaneous inversion of three model parameters with multiple classes of arrival times.ChineseJ.Geophys. (in Chinese), 56(12): 4215-4225, doi: 10.6038/cjg20131224.
Kennett B L N, Sambridge M S, Williamson P R. 1988. Subspace methods for large inverse problems with multiple parameter classes.Geophys.J.Int., 94(2): 237-247.
Kennett B L N, Engdahl E R, Buland R. 1995. Constraints on seismic velocities in the earth from traveltimes.Geophys.J.Int., 122(1): 108-124.
Moser T J. 1991. Shortest path calculation of seismic rays.Geophysics, 56(1): 59-67.
Preston L A. 2003. Simultaneous inversion of 3D velocity structure, hypocenter locations, and reflector geometry in Cascadia [Ph. D. thesis]. Washington: University of Washington.
Preston L A, Creager K C, Grosson R S, et al. 2003. Intraslab earthquakes: Dehydration of the Cascadia slab.Science, 302(5648): 1197-1200.
Rawlinson N, Sambridge M. 2004. Multiple reflection and transmission phases in complex layered media using a multistage fast marching method.Geophysics, 69: 1338-1350.
Rawlison N, Sambridge M S. 2003. Seismic traveltime tomography of the crust and lithosphere.AdvancesinGeophysics, 46: 81-198. Sambridge M S. 1990. Non-linear arrival time inversion: Constraining velocity anomalies by seeking smooth models in 3-D.Geophys.J.Int., 102(3): 653-677. Sambridge M S, Kennett B L N. 1990. Boundary value ray tracing in a heterogeneous medium: A simple and versatile algorithm.Geophys.J.Int., 101(1): 157-168.
Snoke J A, Lahr J C. 2001. Locating earthquakes: At what distance can the earth no longer be treated as flat?Seism.Res.Lett., 72(5): 538-541.
Su W J, Woodward R L, Dziewonski A M. 1994. Degree 12 model of shear velocity heterogeneity in the mantle.J.Geophys.Res., 99(B4): 6945-6980.
Tang X P, Bai C Y. 2009a. Multiple ray tracing in 2D layered media with the shortest path method.ProgressinGeophysics(in Chinese), 24(6): 2087-2096, doi: 10.3969/j.issn.1004-2903.2009.06.022.
Tang X P, Bai C Y. 2009b. Multiple ray tracing within 3-D layered media with the shortest path method.ChineseJ.Geophys. (in Chinese), 52(10): 2635-2643, doi: 10.3969/j.issn.0001-5733.2009.10.024.
Tian Y, Huang S H, Nolet G, et al. 2007. Dynamic ray tracing and traveltime corrections for global seismic tomography.J.Comp.Phys., 226(1): 672-687.
Van der Hilst R D, Widiyantoro S, Engdahl E R. 1997. Evidence for deep mantle circulation from global tomography.Nature, 386(6625): 578-584.
Vidale J E. 1998. Finite-difference calculation of travel times.Bull.Seism.Soc.Am., 78(6): 2062-2076.
Vidale J E. 1990. Finite-difference calculation of traveltimes in three dimensions.Geophysics, 55(5): 521-526.
Zhao D P, Hasegawa A, Horiuchi S. 1992. Tomographic imaging of P and S wave velocity structure beneath northeastern Japan.J.Geophys.Res., 97(B13): 19909-19928.
Zhao D P, Lei J S. 2004. Seismic ray path variations in a 3D global velocity model.Phys.EarthPlanet.Inter., 141(3): 153-166.
Zhao D P, Todo S, Lei J S. 2005. Local earthquake reflection tomography of the Landers aftershock area.EarthPlanet.Sci.Lett., 235(3-4): 623-631.
Zhao R, Bai C Y. 2010. Fast multiple ray tracing within complex layered media: The shortest path method based on irregular grid cells.ActaSeismologicaSinica(in Chinese), 42(4): 433-444.
附中文参考文献
白超英, 黄国娇, 李忠生. 2011. 三维复杂层状介质中多震相走时联合反演成像. 地球物理学报, 54(1): 182-192, doi: 10.3969/j.issn.0001-5733.2011.01.019.
黄国娇, 白超英. 2010. 二维复杂层状介质中地震多波走时联合反演成像. 地球物理学报, 53(12): 2972-2981, doi: 10.3969/j.issn.0001-5733.2010.12.021.
黄国娇, 白超英. 2013. 多震相走时联合三参数同时反演成像. 地球物理学报, 56(12): 4215-4225, doi: 10.6038/cjg20131224.
唐小平, 白超英. 2009a. 最短路径算法下二维层状介质中多次波追踪. 地球物理学进展, 24(6): 2087-2096, doi: 10.3969/j.issn.1004-2903.2009.06.022.
唐小平, 白超英. 2009b. 最短路径算法下三维层状介质中多次波追踪. 地球物理学报, 52(10): 2635-2643, doi: 10.3969/j.issn.0001-5733.2009.10.024.
赵瑞, 白超英. 2010. 复杂层状模型中多次波快速追踪: 一种基于非规则网格的最短路径算法. 地震学报, 42(4): 433-444.
(本文编辑 何燕)
Simultaneous inversion of three model parameters with multiple phases of arrival times in spherical coordinates
HUANG Guo-Jiao1, BAI Chao-Ying2, QIAN Wei1
1DepartmentofGeologyScience&Engineering,SchoolofEarthSciencesandEngineering,HohaiUniversity,Nanjing211100,China2DepartmentofGeophysics,CollegeofGeologyEngineeringandGeomatics,Chang′anUniversity,Xi′an710054,China
To guarantee computational precision and improve the resolution of seismic traveltime tomography at a regional or global scale, we conduct a 3D simultaneous inversion of three different parameters (velocity, hypocenter location and reflector geometry) in spherical coordinates with multi-phase travel times. For this task, there are two key issues: (1) It needs an efficient and accurate arrival tracking algorithm for multiply transmitted, reflected (or refracted) and converted waves in a 3D variable velocity model with embedded velocity discontinuities (or subsurface interfaces), and (2) A subdimensional inversion solver is required which can easily search for different types of model parameters to balance the tradeoff between the different types of model parameter updated in the simultaneous inversion process.For these purposes, we first extend a popular grid/cell-based wavefront expanding ray tracing algorithm (the multistage irregular shortest-path ray tracing method, shorted as ISPM), which previously worked only in Cartesian coordinates at a local scale, to spherical coordinates appropriate to a regional or global scale. In 3D spherical coordinates a trapezoidal prism cell is used to divide the spherical earth model, except for the global and other irregular subsurface interfaces, where a trapezoidal cone is used. And in one previous paper we have discussed the computational accuracy of the multistage ISPM algorithm against the analytic solution of AK135 Travel Time Table for 49 kinds of global phases and concluded that the computational accuracy can be tuned to within the 0.1 s absolute time error when it works in the spherical coordinates. We then incorporate the subspace method to formulate a simultaneous inversion algorithm, in which the multiple classes of arrivals (including direct and reflected arrivals from different velocity discontinuities) can be used to simultaneously update the velocity fields, hypocenter location and reflector geometries.In order to illustrate the performance of inversion for three model class parameters, we have selected a regional model at a scale of 20°×20°×700 km. In the numerical experiment, different phases are used. For comparison, we design three different schemes. The first one is to simultaneously update both the velocity field and the source locations (referred as V+S inversion), the second is to simultaneously invert both the velocity field and the reflector positions (referred as V+R inversion), while the third scheme updates all three model parameter classes simultaneously (referred as V+R+S inversion). To account for picking uncertainty, random noise was added to the multiple sets of arrivals according to the expected picking errors. The inversion results show that the reconstructed velocity fields exhibit similar anomalous structures to the true field, but only partially being recovered. Interestingly, the recovered velocity fields are nearly the same regardless whether the two parameter class inversion or three parameter class inversion is attempted. The updated two subsurface interfaces are almost identical, no matter whether the V+R or the V+R+S simultaneous inversion algorithm is used. For the hypocenter location, the V+S inversion has a slightly better convergence to the real source locations than the V+R+S inversion, due to only two classes of the model parameters being updated in the simultaneous inversion process, but the difference is not so significant.The above results verify that the V+R+S simultaneous inversion scheme is feasible and applicable due to the almost equal capability with the constrained two model parameter class inversions (V+S or V+R). All three scheme algorithms are quite tolerant to modest errors in the travel time picks, which makes them robust enough for practical applications. The results show that the V+R+S simultaneous inversion method is an efficient and feasible scheme for updating the velocity field, reflector geometry and hypocenter location.
Spherical coordinates; Multistage irregular shortest-path method; Multi-phase travel times; Simultaneous inversion of three model parameters; Subspace method
10.6038/cjg20151016.
Huang G J, Bai C Y, Qian W. 2015. Simultaneous inversion of three model parameters with multiple phases of arrival times in spherical coordinates.ChineseJ.Geophys. (in Chinese),58(10):3627-3638,doi:10.6038/cjg20151016.
江苏省自然科学基金项目(BK20150799)、国家自然科学基金项目(41504038)、河海大学中央高校基本科研业务费项目(2014B13814)、教育部博士学科专项基金项目(20110205110010)资助.
黄国娇,女,1987年4月生于湖北省随州市,主要从事地震正、反演方法及应用研究.E-mail: jiaojiao.1986520@163.com
10.6038/cjg20151016
P315
2014-12-22,2015-06-16收修定稿
≤≥≪ ≫黄国娇, 白超英, 钱卫. 2015. 球坐标系下多震相走时三参数同时反演成像.地球物理学报,58(10):3627-3638,

