模拟分析低低跟踪模式重力卫星反演地球重力场的精度

冉将军， 钟敏*， 许厚泽， 周泽兵， 万晓云

1 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室， 武汉 430077 2 华中科技大学物理学院， 武汉 430074 3 钱学森空间技术实验室， 北京 100094



模拟分析低低跟踪模式重力卫星反演地球重力场的精度

冉将军1， 钟敏1*， 许厚泽1， 周泽兵2， 万晓云3

1 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室， 武汉 430077 2 华中科技大学物理学院， 武汉 430074 3 钱学森空间技术实验室， 北京 100094

本文利用卫星重力反演与模拟软件ANGELS系统(ANalyst of Gravity Estimation with Low-orbit Satellites)对低低跟踪模式的重力卫星的关键载荷精度指标进行了深入分析.模拟结果表明: (1) 对短弧长积分法而言，在低低跟踪模式的关键载荷精度指标中，重力场反演精度对星间距离变率精度最为敏感； (2) 通过对目前在轨运行GRACE的载荷指标进行分析，发现轨道数据的误差主要影响重力场的低阶部分(约小于25阶)，较高阶次部分(约大于26阶)主要受星间距离变率的误差限制； (3) 如果下一代低低跟踪模式的重力卫星的目标之一是把重力异常反演精度较GRACE提高约10倍，则在保持轨道高度和GRACE相同的前提下，轨道、星间距离变率和星载加速度计等关键载荷指标需要达到的最低精度分别约为2 cm、10 nm·s-1和3.0×10-10m·s-2； (4) 轨道精度和混频误差将是影响下一代低低跟踪模式重力卫星重力场恢复能力进一步提高的主要制约因素，距离变率精度和加速度计精度存在盈余.

低低跟踪模式； 关键载荷； GRACE； 重力异常； 短弧长积分法

1 引言

地球重力场是地球基本物理场之一，因此精确测定地球重力场一直是国内外大地测量学者们的重要研究目标.重力卫星以其全球覆盖、测量时间长和精度高等优势逐渐成为中低阶地球重力场模型确定的主要观测方法.截至目前，重力卫星经历了卫星跟踪卫星高低模式、卫星跟踪卫星低低模式和卫星重力梯度模式，分别以CHAMP(Challenging Mini-Satellite Payload for Geophysical Research and Application)、GRACE(Gravity Recovery and Climate Experiment)和GOCE(Gravity Field and Steady- state Ocean Circulation Explorer)为代表(Reigber et al., 2003; Tapley and Bettadpur, 2004; Pail et al., 2011).其中基于卫星跟踪卫星低低模式的GRACE重力卫星以其具有高时空分辨率地监测地球的质量分布信息的能力被国内外科学界格外重视(Tapley and Bettadpur, 2004; Chen et al., 2006; Wouters et al., 2008).发射于2002年的GRACE重力卫星已经连续在轨运行近12年，即将停止运行，因此国内外同行对发射后续的低低跟踪模式的重力卫星进行了大量指标论证和仪器研制等相关的研究.如，国际同行Sneeuw 和Schaub (2005), Watkins(2007), Reubelt 等(2010), Sharifi等 (2007), Bender等(2008), Loomis 等(2003), Elsaka(2010), Visser等,(2010), Wiese (2011)利用解析法、短弧长法或者动力学法对单组或多组低低跟踪模式重力卫星关键载荷指标的敏感性、轨道参数选取以及时变信号提取等问题进行了深入研究.国内同行中，赵倩(2012)和姜卫平等(2014)重点研究了卫星的轨道参数选取和编队模式；郑伟(2007)和冉将军等(2012)重点分析了卫星主要载荷指标的敏感性.

在进行编队模式的研究前，必须对指标敏感性有深入的认识，以保证对解算结果解释的正确性.到目前为止，国内同行对指标的分析，主要采用如下方法: 对所研究的某项指标(比如，星间距离变率)添加不同精度的误差(如2.0×10-7m·s-1, 1.0×10-8m·s-1和1.0×10-9m·s-1)，其余指标(比如，轨道精度和加速度计精度)选择GRACE卫星设计指标的误差，从而分析该指标(如距离变率)对地球重力场反演的影响.此方法具有实际意义，因为它把GRACE卫星作为基准.但仍可以从以下两方面进行改进.第一、除了所需要研究的指标(比如，距离变率精度)外，其余指标(比如，轨道和加速度计)也含有误差，各种载荷误差相互影响，相互制约，因此难以分清某项指标单独对重力场反演精度的影响.在这方面，国际同行中，Watkins(2007)和Wiese(2011)利用动力学法对重力卫星的关键指标单独对重力场反演精度进行了讨论，而国内同行则罕有涉及.第二、在模拟GRACE数据反演地球重力场时，给距离变率数据加入均值为0，方差为1.0×10-6m·s-1的白噪声通常是大部分同行的选择，而事实上GRACE实测数据结果显示其距离变率的精度在约2.0×10-7m·s-1的水平(冉将军，2013).因此作者在本文根据实测GRACE距离变率处理经验，在对低低跟踪模式重力卫星模拟分析时，添加更为符合实际情况的误差，使模拟结果更为可靠.

本文中，作者首先利用地球重力场反演与模拟系统ANGELS(ANalyst of Gravity Estimation with Low-orbit Satellites)的短弧长积分法模块分析低低跟踪模式重力卫星的关键指标单独对重力场反演精度的敏感性.进而，在基于下一代低低跟踪模式重力卫星的目标之一是把重力异常反演精度提高10倍的假设下，对满足此目标的关键载荷的最低要求进行探讨，以期节省不必要研究成本.

2 短弧长积分法的函数模型

(1)

其中

(2)

式中，rA和rB表示弧段的端点坐标，t表示时间，τ=(t-tA)/T为归一化的时间，T=tB-tA为弧长(本文选择30min)，tA和tB分别表示弧段端点的时间.

如果把弧段边界位置和重力场位系数当作参数，则上式可变形为

r(τ)=rA(1-τ)+rBτ-KGβ，

(3)

其中β表示地球重力场球谐系数，G表示力对地球重力位系数的偏导数矩阵.

对于GRACE卫星的低低卫卫跟踪模式，把两颗卫星的位置或速度在视线方向做投影，可得到星间距离或星间距离变率的函数关系如下:

ρ=Δr12e12，

(4)

(5)

上述内容给出了短弧长积分法的基本函数模型.现在导出星间距离变率和未知参数(边界位置b1和b2、重力场模型参数β、加速度计尺度偏差参数BSP1和BSP2)的函数模型.如图1所示，星间距离变率实际上是卫星速度差在视线方向的投影.其中，A和B分别表示弧段边界点.

图1 星间距离变率示意图Fig.1 Schematic diagram of range rate between two satellites

(6)

(7)

其中

(8)

(9)

(10)

(11)

(12)

这里把边界轨道参数b1、b2以及加速度计参数BSP当做未知参数与球谐系数δβ一起平差，如下所示：

l=AX，

(13)

其中

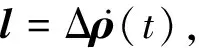
(14)

(15)

(16)

利用最小二乘准则联合轨道和星间距离变率或星间距离即可进行求解重力场位系数(Mayer-Gürr, 2006; 冉将军, 2013).

3 关键载荷的深入分析

3.1 软件的正确性验证

为了验证该系统的可靠性，把利用ANGELS系统(ANalyst of Gravity Estimation with Low-orbit Satellites)解算的IGG-CAS 01系列时变地球重力场模型与国际权威机构美国德克萨斯大学奥斯汀分校空间中心CSR (Center for Space Research)解算的最新版同类产品CSR-RL05进行比较.常用的时变地球重力场模型的比较方式有两种: 第一种是从频域的角度比较每阶大地水准面差距(或者重力异常和阶方差等)；第二种是比较由模型提取出的时变信号.关于IGG-CAS 01模型与CSR-RL05模型的每阶大地水准面的差距比较在冉将军(2013)做了详尽的分析.本文重点利用第二种比较方法对模型进行验证.

图2给出了经过相同的去条带和高斯滤波处理后，算出的2004到2010年间IGG-CAS 01和CSR-RL05模型在中国大陆的地表质量变化趋势.从图2可知，IGG-CAS 01和CSR算出的趋势在空间分布上非常接近，两者的相关系数约0.9.在华北地区存在明显的质量缺失，具体原因可能是由于地下水过度开采导致.此外，在新疆地区也存在大量的质量减少，其中心位于天山山脉附近，该地区的冰盖也在逐年融化.而图2中显示出的质量变化是否就是由于冰盖减少导致，仍然有待进一步深入的研究.在中国的西部地区喜马拉雅山脉附近存在非常显著的质量减少，该地区的质量变化是近年来的研究热点之一，具体由何种因素导致，仍然众说纷纭(Bolch et al., 2012; Scherler et al., 2011; Gardelle et al., 2011).本节的重点在于验证ANGELS的正确性，因此不对该问题过多讨论.

图3表示把CSR RL05和IGG-CAS 01从2004年到2010年的时变地球重力场模型做半波长同为250 km的高斯滤波后得到的格陵兰岛冰川质量变化趋势.如图所示，IGG-CAS 01解算的2004年到2010年格陵兰岛冰川的质量变化趋势与CSR RL05趋势的结果非常接近(相关系数约0.9)，两组模型都表明: 在格陵兰岛中南部和西北部冰川的质量减少趋势明显，东北部表现为略微的质量增加，中部质量变化趋势缓慢.

图2和图3的综合比较结果验证了利用ANGELS系统进行重力场解算的可行性和可靠性.

3.2 星间距离变率精度对反演地球重力场的影响

为了研究距离变率测量精度单独对重力场反演精度的影响，现基于短弧长积分法，模拟轨道高度为500 km(本文所有的模拟情况都基于此轨道高度)、采样率为10 s的30天数据(下同)，分析在只给距离变率加入测量误差(本文所添加误差均指白噪声)时对重力场反演精度的影响.

从图4可知，星间距离变率精度从10 nm·s-1、5 nm·s-1到1 nm·s-1时，反演重力场的精度逐渐接近重力场反演的极限水平(error free).星间距离变率测量精度为2.0×10-7m·s-1时的重力场反演精度从20阶开始低于由上述三种情况下重力场反演精度一个量级左右，但远高于目前GRACE卫星所达到的水平(图4中GRACE real data表示用一个月实测GRACE level1B数据解算的重力场模型的每阶大地水准面差距，下同).因为GRACE卫星的数据里实际上并不是仅距离变率包含误差的理想状况，其余数据(轨道和加速度等)也包含误差，从而限制了微波测量系统对重力场反演的贡献.

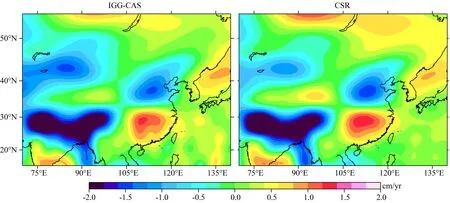
图2 中国大陆地表质量在2004—2010年间变化趋势(色标为等效水柱高，单位cm/yr)(a)IGG-CAS 01模型；(b)国际知名机构CSR发布的RL05版GRACE产品.Fig.2 Trend of mass anomaly in the mainland of China from 2004 to 2010(a) IGG-CAS 01； (b) CSR RL05.

图3 IGG-CAS 01和CSR RL05在2004—2010年间格陵兰岛冰川的质量变化趋势(色标为等效水柱高，单位m/yr)(a) IGG-CAS 01; (b) CSR RL05.Fig.3 Trend of mass anomaly in Greenland over 2004—2010 (Equivalent water height, unit: m/yr)

图4 星间距离变率含误差、其余载荷无误差时的重力场反演精度Fig.4 Geoid height error when only range rate measurements contaminated by different error

3.3 星间距离精度对反演地球重力场的影响

虽然低低跟踪模式数据系统也提供星间距离数据，但由于在实际测量中，星间距离数据通常含有偏差，因此对GRACE重力卫星而言，几乎很少有人利用星间距离数据去反演地球重力场模型.鉴于星间距离仍然具有一定的反演重力场的潜力，本文仍对其进行与星间距离变率类似的分析，以了解星间距离对重力场反演的影响.

表1 不同星间距离精度反演的重力场模型的累计大地水准面精度(m)Table 1 Cumulative geoid height error of recovered gravity field models with different accuracy of range data (m)

图5 星间距离含误差、其余载荷无误差时的重力场反演精度Fig.5 Geoid height error when only range measurements contaminated by different error

从图5可知，星间距离精度在100 nm、50 nm和10 nm时，重力场恢复的精度差别不大，都高于目前GRACE实测数据所能达到的水平.表1为100 nm、50 nm和10 nm的星间距离精度反演的地球重力场模型的累计大地水准面误差，从第三阶开始累积到120阶的累计大地水准面误差分别约为1.645 cm，1.645 cm和1.651 cm.

3.4 星载加速度计精度对反演地球重力场的影响

星载加速度计主要测量包括大气阻力、地球辐射压、轨道高度和姿态控制力等非保守力.GRACE卫星搭载的星载加速度计目前所能达到的量级约为3.0×10-10m·s-2.为了深入分析非保守力的测量精度对重力场反演的影响，下面讨论仅加速度计观测值包含误差时的重力场恢复能力.

图6 加速度计含误差、其余载荷无误差时的重力场反演精度Fig.6 Geoid height error when only accelerometer measurements contaminated by different error

从图6可知，在目前GRACE卫星所能达到的测量精度(3.0×10-10m·s-2)下，由加速度计导致的误差仍然低于GRACE卫星实测数据反演能力的两个量级左右.虽然图6显示了理想状态下(仅加速度计包含误差，其余指标无误差)加速度计误差对重力场反演的影响较小，但在实际情况下(各关键载荷均含误差)，由于加速度计误差在通过两次积分后，把误差传播到了参考轨道和参考距离变率中，会进一步地降低轨道精度和距离变率精度，从而影响到重力场反演精度的提高，如下文图8所示.如果下一代低低跟踪模式的重力卫星采用drag-free系统，可把重力场反演精度成倍数提高.所以加速度计误差在实际重力卫星数据处理中仍占重要位置，不可忽略.

3.5 低轨卫星定轨精度对反演地球重力场的影响

轨道作为重力卫星的关键载荷之一，应用在重力场反演数据处理的各个环节，如参考轨道和参考星间距离变率等.换言之，如果轨道数据质量较差，不仅影响利用轨道数据反演地球重力场的精度，还将影响利用星间距离变率数据反演地球重力场的能力.因此，轨道精度对利用重力卫星数据的重力场反演可谓至关重要.为了研究轨道对重力场反演的具体影响，现对轨道单独添加均值为0，方差分别为2 mm、2 cm和5 cm的白噪声，所反演的重力场模型的每阶大地水准面精度如图7.

图7 轨道含误差、其余载荷无误差时的重力场反演精度Fig.7 Geoid height error when only orbit measurements contaminated by different error

如图7所示，可知重力场恢复精度对轨道精度依赖程度较高(轨道高度除外)，相比图4、图5和图6，轨道对重力场反演精度的影响较大.2 cm的轨道数据所反演的重力场模型精度仍然高于目前GRACE实测数据反演的重力场约一个量级，说明就目前GRACE卫星的载荷精度而言，2 cm的轨道精度仍有盈余.当把轨道精度从2 cm提高到2 mm时，重力场恢复精度近乎等量级提升，5 cm的轨道精度反演的重力场模型精度最差.

4 低低跟踪模式重力卫星重力场反演精度制约因素的综合评估

上述分析了低低跟踪模式重力卫星的关键载荷单独含误差时，对重力场反演的影响，现以目前在轨的GRACE卫星的实际载荷精度为例，分析影响其重力场反演精度的关键制约因素，为下一代重力卫星的指标提供参考.

图8 关键载荷对重力场反演精度的影响Fig.8 Impact from the key payloads to the accuracy of gravity field modeling

图8所示的星型线为基于短弧长积分法融合轨道和距离变率数据在轨道、星间距离变率和星载加速度计精度分别为2 cm、2.0×10-7m·s-1和3.0×10-10m·s-2时，反演的地球重力场模型的每阶大地水准面差距，本文简称组合解1，其中轨道和星间距离变率的权根据轨道和星间距离变率先验信息确定(冉将军等，2012).

图中“orbit 2 cm”和“range rate 2.0×10-7m·s-1”表示除指定的指标外，其他指标不含误差的重力场反演结果，但为了保持一致性和可比性，此时仍然采用与组合解1相同的权.值得注意的是，这里同样是利用给某指定的指标单独添加误差后的数据反演的重力场，但却分别比图4和图7所示的相应结果的精度低很多.这是因为图4和图7的结果是假设仅轨道和星间距离变率包含误差的理想状况，而本节的目的是尽可能真实地分析关键载荷对GRACE卫星重力场反演的影响程度，所以在组合解1里对三种关键载荷都添加误差.在本节轨道/距离变率单独含误差的算例里(“orbit 2 cm”和“range rate 2.0×10-7m·s-1”)，通过保持与组合解1相同的权，即可保持可比性，又可以通过限制无误差的其余关键载荷的贡献，使得分析结果更可靠.

根据反演结果可知，组合解1的低阶部分(前25阶)由轨道确定，其余部分由距离变率限制，而加速度计精度存在盈余.如果仅用轨道数据反演地球重力场模型即可发现所反演的地球重力场模型在25阶左右往后误差快速增加，此时则需要引入对地球重力场高阶较敏感的距离变率数据来降低噪声.图8中所示的精度曲线”orbit 2 cm rr”在约25阶以前较大，是由轨道数据包含2 cm的误差所致，而在25阶到120阶时精度较高，是由于此频段的重力场信息主要由无误差的距离变率数据提供.

基于上述关于低低跟踪模式关键载荷对重力场反演精度的单独分析和目前GRACE卫星重力场反演精度的关键制约因素研究，下面利用短弧长积分法对可能采用激光干涉测距系统的下一代低低跟踪模式重力卫星的重力场反演精度进行分析.

如果下一代低低跟踪模式的重力卫星计划的预期目标之一是把月尺度的重力异常反演精度提高10倍，则弄清满足此要求的关键载荷的最低精度，有助于降低载荷研制难度和节省成本.通过对上述关键载荷的分析可知，对低低跟踪模式重力场反演精度影响较大的因素为轨道精度和星间距离变率精度.从图8 可知，2 cm的轨道精度对目前的重力场反演而言仍有盈余，而2.0×10-7m·s-1的距离变率精度没有盈余，因此如果要将下一代低低跟踪模式的重力卫星重力场反演精度提高，首要考虑的就是提高距离变率精度.

图9中“Combination: orbit 2 cm & range rate 10 nm·s-1& acc 3.0×10-10m·s-2”表示利用2 cm、10 nm·s-1和3.0×10-10m·s-2的轨道精度、星间距离变率精度和星载加速度计精度所反演的地球重力场模型的每阶大地水准面差距，本文简称组合解2，其累积重力异常精度详见表2.组合解2 即表示将距离变率精度较GRACE提高约1个量级后的重力场反演结果.从图可知，混频误差(图中标为“aliasing”的曲线)与轨道误差(图中标为的“orbit 2 cm rr”的曲线)对重力场反演精度的影响大于其余载荷的影响，这两种误差将对下一代重力卫星的重力场恢复能力的进一步提高起到相当大的制约作用.对组合解2而言，其精度接近于轨道单独含误差(图中标为“Orbit 2 cm rr”的曲线)时的重力场反演精度.如图9所示，通过比较约从第25阶开始的组合解1和组合解2的每阶大地水准面差距，可知组合解2高于组合解1约1个量级左右.组合解1和组合解2在120阶(半波长约为167 km的空间分辨率)的累积重力场异常精度/累计大地水准面精度分别为1.67Gal/9.65cm和302mGal/1.76cm.

图9 重力卫星重力场反演精度的制约因素Fig.9 Key impact sources to gravity field modeling

表2 两种组合解的累积重力异常精度(Gal)Table 2 Cumulative gravity anomaly per degree of two combined solutions (Gal)

5 结论

通过实际地学信号的提取验证了地球重力场反演系统ANGELS(ANalyst of Gravity Estimation with Low-orbit Satellites)的可靠性，并将其用于低低跟踪模式重力卫星指标的敏感性研究.通过利用短弧长积分法单独对某一种指标添加误差，其余指标不含误差，分析了该指标对重力场反演精度的影响，并对可能采用激光干涉测距系统的下一代低低跟踪模式重力卫星的重力场反演精度进行分析，得到如下结论.

(1) 对短弧长积分法而言，在低低跟踪模式的关键载荷中，重力场反演精度对星间距离变率精度最为敏感.

(2) 从误差的角度，通过对目前在轨运行的GRACE的关键制约因素的分析发现轨道数据的误差主要影响重力场的低阶部分，较高阶次部分主要受制于星间距离变率的误差.

(3)如果下一代低低跟踪模式的重力卫星的目标之一是把重力场异常反演精度较GRACE提高约10倍，则轨道、星间距离变率和星载加速度计等关键载荷需要达到的最低精度分别约为2 cm、10 nm·s-1和3.0×10-10m·s-2.

(4)轨道精度和混频将是影响下一代低低跟踪模式重力卫星重力场恢复能力进一步提高的主要制约因素.

Bender P L, Wiese D N, Nerem R S. 2008. A possible dual-GRACE mission with 90 degree and 63 degree inclination orbits. ∥Proceedings of the Third International Symposium on Formation Flying, Missions and Technologies, ESA/ESTEC, Noordwijk, The Netherlands.Bolch T, Kulkarni A, Kääb A, et al. 2012. The state and fate of Himalayan glaciers.Science, 336(6079): 310-314.

Chen J L, Wilson C R, Tapley B D. 2006. Satellite gravity measurements confirm accelerated melting of Greenland ice sheet.Science, 313(5795):1958-1960, doi:10.1126/science.1129007.

Elsaka B. 2010. Simulated satellite formation flights for detecting the temporal variations of the Earth's gravity field [Ph. D. thesis]. Bonn: University of Bonn.

Gardelle J, Arnaud Y, Berthier E. 2011. Contrasted evolution of glacial lakes along the Hindu Kush Himalaya mountain range between 1990 and 2009.GlobalPlanet.Change, 75(1-2): 47-55.

Jiang W P, Zhao W, Zhao Q, et al. 2014. Satellite formation for a new gravity field exploration mission.ActaGeodaeticaetCartographicaSinica(in Chinese), 43(2):111-117. doi:10.13485/j.cnki.11-2089.2014.0016.

Loomis B. 2003. Simulation study of a follow-on gravity mission to GRACE. Boulder: University of Colorado.

Mayer-Gürr T. 2006. Gravitationsfeldbestimmung aus der Analyse kurzer Bahnböegen am Beispiel der Satellitenmissionen CHAMP und GRACE. Bonn: University of Bonn.

Pail R, Bruinsma S, Migliaccio F, et al. 2011. First GOCE gravity field models derived by three different approaches.JournalofGeodesy, 85(11): 819-843.

Ran J J, Xu H Z, Shen Y Z, et al. 2012. Expected accuracy of the global gravity field for next GRACE satellite gravity mission.ChineseJournalGeophysics(in Chinese), 55(09):

2898-2908, doi: 10.6038/j.issn.0001-5733.2012.09.009.

Ran J J. 2014. Theory, methodology and application of gravity field recovery using low-low tracking gravity satellite data [Ph. D. thesis] (in Chinese). University of Chinese Academy of Sciences.Reigber C, Schwintzer P, Neumayer K -H, et al. 2003. The CHAMP-only Earth gravity field model EIGEN-2.AdvancesinSpaceResearch, 31(8): 1883-1888.

Reubelt T, Sneeuw N, Sharifi M A. 2010. Future mission design options for spatio-temporal geopotential recovery. ∥Mertikas S P, ed. Gravity, Geoid, and Earth Observation. Berlin Heidelberg: Springer, 163-170.

Scherler D, Bookhagen B, Strecker M R. 2011. Spatially variable response of Himalayan glaciers to climate change affected by debris cover.NatureGeosci., 4(3): 156-159

Sharifi M, Sneeuw N, Keller W. 2007. Gravity recovery capability of four generic satellite formations. ∥ Kilicoglu A, Forsberg R, eds. Gravity field of the Earth. General Command of Mapping, ISSN 1300-5790, Special Issue 18, 211-216.

Sneeuw N, Schaub H. 2005. Satellite clusters for future gravity field missions. ∥Jekeli C, Bastos L, Fernandes J, eds. Gravity, Geoid and Space Misssions. Berlin Heidelberg: Springer, 12-17.Tapley B D, Bettadpur S. 2004. The gravity recovery and climate experiment: Misson overiew and early results.Geophys.Res.Lett., 31(9): L09607, doi: 10.1029/2004GL019920.

Visser P N A M, Sneeuw N, Reubelt T, et al. 2010. Space-borne gravimetric satellite constellations and ocean tides: aliasing effects.GeophysicalJournalInternational, 181(2): 789-805.

Watkins M. 2007. The future of gravity satellite. Workshop in Noordwijk, the Netherlands.

Wiese D N. 2011. Optimizing two pairs of GRACE-like satellites for recovering temporal gravity variations [Ph. D. thesis]. Boulder: University of Colorado.Wouters B, Chambers D, Schrama E J O. 2008. GRACE observes small-scale mass loss in Greenland.Geophys.Res.Lett., 35(20): L20501, doi: 10.1029/2008GL034816.

Zhao Q. 2012. Methodology research and simulation analysis of the Earth′s gravity field determination using satellite formation. [Ph. D. thesis] (in Chinese). Wuhan: Wuhan University, China.

Zheng W. 2007. Theory and methodology of Earth's gravitational field recovery based on satellite gravity measurement [Ph. D. thesis] (in Chinese). Wuhan: Huazhong University of Science and Technology.

附中文参考文献

姜卫平, 赵伟, 赵倩等. 2014. 新一代探测地球重力场的卫星编队. 测绘学报, 43(2): 111-117.

冉将军, 许厚泽, 沈云中等. 2012. 新一代GRACE重力卫星反演地球重力场的预期精度. 地球物理学报, 55(9): 2898-2908, doi: 10.6038/j.issn.0001-5733.2012.09.009.

冉将军. 2013. 低低跟踪模式重力卫星反演理论、方法及应用[博士论文]. 北京: 中国科学院大学.

赵倩. 2012. 利用卫星编队探测地球重力场的方法研究与仿真分析[博士论文]. 武汉: 武汉大学.

郑伟. 2007. 基于卫星重力测量恢复地球重力场的理论和方法[博士论文]. 武汉: 华中科技大学.

(本文编辑 胡素芳)

Analysis of the gravity field recovery accuracy from the low-low satellite-to-satellite tracking mission

RAN Jiang-Jun1, ZHONG Min1*, XU Hou-Ze1, ZHOU Ze-Bing2, WAN Xiao-Yun3

1StateKeyLaboratoryofGeodesyandEarth′sGeodynamicsChineseAcademyofSciences,Wuhan430077,China2SchoolofPhysics,HuazhongUniversityofScienceandTechnology,Wuhan430074,China3QianXuesenLaboratoryofSpaceTechnology,Beijing100094,China

Gravity Recovery And Climate Experiment mission (GRACE), which was launched in 2002, has provided a viable way to investigate the mass variations happened on the Earth surface. GRACE, however, will terminate in the near future. Thus many research groups begun to propose the next generation of low-low satellite to satellite tracking mission, such as the GRACE Follow-On mission from the National Aeronautics and Space Administration and the German Aerospace Center, the Earth System Mass Transport Mission (e.motion) from the European Space Agency, and China′s future satellite gravity mission. In this paper, we focus on the simulation study of China′s future satellite gravity mission which is proposed by Chinese Academy of Sciences, cooperating with Huazhong University of Science and Technology, Aerospace Dongfanghong Satellite Company and so on. One of the goals of China′s future satellite mission is to improve the accuracy of the gravity field model by a factor of 10, compared with that of GRACE. To that end, the minimum requirements of the key payloads are of great importance to be clarified. Here we try to answer this research question by numerical simulations.Several methodologies have been widely used to process the data collected by GRACE mission, such as variation equation approach, acceleration approach, energy integral approach and short arc approach. Because of small accumulative numerical integration error and stronger flexibility to deal with data gaps, short arc approach is selected and applied to do the analysis in this work. Based on short arc approach, a software named ANalyst of Gravity Estimation with Low-orbit Satellites (ANGELS) was developed by us. In order to validate the output produced by ANGELS, a new series of monthly gravity field model named IGG-CAS 01, which was truncated up to degree/order 60, was recovered using ANGELS. By comparing the mass variation trends at both Greenland and China from 2004 to 2010 computed from IGG-CAS 01 and CSR RL05, we find the correlation number are around 0.9, which confirms that IGG-CAS 01 is comparable with CSR RL05.Finally, ANGELS was used to analyze the key payloads of the low-low satellite-to-satellite tracking mission in this study. The numerical results show: (1) the precision of range rate, as for short arc approach, is the most sensitive impact factor compared with other payloads of the low-low satellite-to-satellite tracking mission； (2) by analyzing the error budget of the ongoing GRACE mission in terms of geoid height per degree, the error in orbit position is the major error source for degrees which are smaller than ～25, while the error of range rate dominates for degrees which are larger than ～26; (3) aiming to improve the gravity field model recovery accuracy by a factor of 10, the minimum requirements of the accuracies of orbit position, range rate and acceleration are 2 cm, 10 nm·s-1and 3.0×10-10m·s-2, respectively; (4) the accuracy of orbit position and the error of de-aliasing model will be the two major error sources of next low-low satellite-to-satellite tracking gravity satellite mission.

The Low-Low Satellite-to-Satellite Tracking Mission； Key payloads； GRACE； Gravity anomaly； Short arc integral approach

10.6038/cjg20151005.

Ran J J, Zhong M, Xu H Z, et al. 2015. Analysis of the gravity field recovery accuracy from the low-low satellite-to-satellite tracking mission.ChineseJ.Geophys. (in Chinese),58(10):3487-3495,doi:10.6038/cjg20151005.

国家重大科学研究计划(2013CB733305)，国家自然科学基金(41174066和41404019)，中国科学院国家外专局“创新团队国际合作伙伴计划”(KZZD-EW-TZ-05)和国家留学基金(2011491203)资助.

冉将军，男，1986年生，中国科学院测量与地球物理研究所博士，主要从事重力卫星数据处理: 轨道确定、重力场模型反演及其地学应用.E-mail: j.ran@tudelft.nl

*通讯作者 钟敏，男，1964年生，博士生导师，研究员，主要从事动力大地测量和时变重力场研究.E-mail:zmzm@whigg.ac.cn

10.6038/cjg20151005

P312

2014-09-08，2015-06-07收修定稿

冉将军， 钟敏， 许厚泽等. 2015. 模拟分析低低跟踪模式重力卫星反演地球重力场的精度.地球物理学报，58(10):3487-3495,