大兴安岭落叶松不同采伐强度的最优树高曲线模型1)
朱玉杰 冯国红 董春芳
(森林持续经营与环境微生物工程黑龙江省重点实验室(东北林业大学),哈尔滨,150040)
责任编辑:张 玉。
目前获取树高的方法主要有两种,一种是测高器,一种是树高曲线模型。用于树高测量的仪器主要有:克里斯登测高器、圆筒测高器、普鲁莱测高器、比例测高器、阿布尼水准器、桑托测斜器、PM-5 型桑托测高器、测杆、林分速测镜、光学测树仪、测树罗盘仪,等等,在国内外至今都被较为广泛的使用;但是,使用这些工具进行的树高测量时一般都要求在立地条件较好、地势较为平坦,且这些测高器多为手提式,使用时受人体晃动影响较大。因此,实地测量时,精度和效率都会受到影响,具有很大的局限性[1-2]。胸径是林分中最易获取的调查因子,基于树高-胸径曲线模型推算树高,是获取树高的重要方法。关于树高曲线模型,已有大量的研究[3-15]。国内外研究者用清查和样地数据建立了许多树高曲线模型,主要有线性模型和非线性模型两大类。在应用树高曲线模型获取树高时,为了提高树高的预测精度,往往需要从常用的树高曲线模型中寻找出适合某种树种的最优模型。然而,采伐强度不同,对树高和胸径的生长量影响不同。有些树种,采伐强度不同对胸径的影响较大,对树高的影响不显著,如:姚克平和施向东分别以15年和13年生马尾松(Pinus massonian)为研究对象,结果表明,强度抚育能显著提高马尾松人工林的胸径,对树高生长无明显影响。有些树种,采伐强度不同,对胸径和树高的影响均较显著,如:陈东莉等研究了不同间伐强度后20年生华北落叶松(Larix)人工林的变化,结果表明,抚育间伐后的华北落叶松人工林分平均胸径和树高有明显的变化,其中以强度间伐后林分的胸径、树高变化最明显[16]。可见,对于同一树种,采伐强度不同时采用相同的树高曲线模型进行预测,势必会影响树高的预测精度。若对于同一树种,能够根据采伐强度的强弱分别选择合适的模型,将会使树高的预测精度得到提高。落叶松是大兴安岭地区重要的树种之一,本文对落叶松在不同采伐强度时的最优树高模型进行了遴选,旨在为大兴安岭落叶松林的调查提供参考。
1 研究地概况
试验地设置在黑龙江省大兴安岭林区新林林业局的新林林场。位于黑龙江省西北部,地处大兴安岭伊勒呼里山的东北坡。地理坐标为东经123°41'~125°25',北纬51°20'~52°10'。地势平缓,坡度多在6°以下。海拔相对较高,有明显的山地气候特点。冬季寒冷而漫长,春、秋两季日较差大,且风力较大。土壤种类为棕色森林土,平均厚度为15 cm。气温年较差和日较差都很大,年平均积温不足1 600 ℃,平均气温为-2.6 ℃,全年冻结期约为7 个月,结冰一般在9月下旬,终冻在4月中下旬,8月下旬开始出现初霜,无霜期为90 d 左右;属于寒温带大陆性气候。年降水量513.9 mm,且分布不均,主要降水多集中在7—8月份。全年日照时间约2 357 h,日照百分率为51%~56%。
2 研究方法
选取18 块采伐强度不同的地作为研究样地(见表1),每块样地均为20 m×20 m。应用激光测距仪(型号:TRUPULSE200)和胸径围尺,对18 块样地的树高和胸径进行测量(见表2)。参考国内外相关研究文献,选取应用较普遍、预测精度较高的10种树高曲线模型作为候选模型[17-18](见表3)。

表1 各样地的采伐强度及地理坐标
3 模型回归结果的对比
1stOpt 是一套数学优化分析综合工具软件包,拟合结果主要包括:参数的最佳解、均方差(Mse)、残差平方和(Sse)、相关系数(R)、决定系数(R2)、卡方系数、F 统计、预测值、拟合曲线图等。其中:Mse能够很好地反映出测量的精密度;Sse能反映出影响H 与D 的回归关系之外的一切因素对H 的总变异的作用,Sse越小,回归效果越好;R2的大小可以反映出趋势线的估计值与对应的实际数据之间的拟合程度,R2越大,拟合程度越高,当趋势线的R2等于1或接近1 时,其可靠性最高。本文选取Mse、Sse、R2作为模型优劣的评价标准,结合不同采伐强度获得的胸径和树高的数据,应用1stopt 软件对10 个树高曲线模型进行了回归(见表4)。
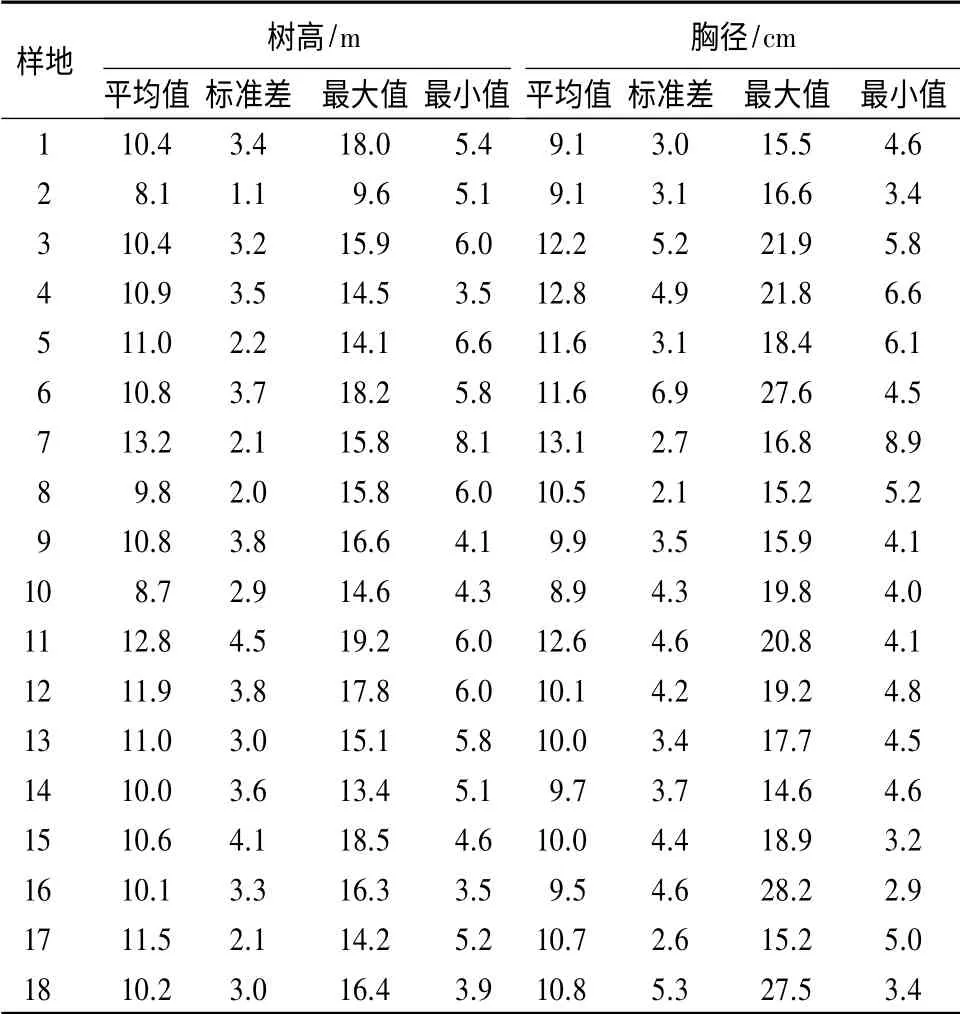
表2 18 块样地树高、胸径的数据处理

表3 10 种树高曲线模型
为了便于比较分析同一树高曲线对于不同采伐强度时树高的预测情况及同一采伐强度时不同树高曲线模型的预测情况,对表4中的同一树高曲线不同采伐强度、同一采伐强度不同树高曲线获得的R2进行了整理(见表5、表6)。

表4 18 块样地10 种模型的回归结果
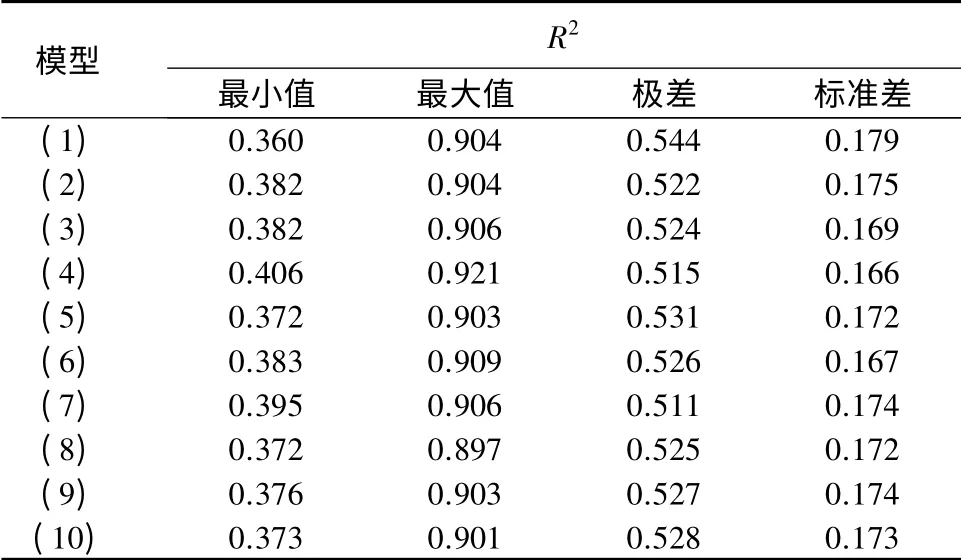
表5 同一树高曲线、不同采伐强度的R2
比较表5中同一树高曲线在18 种采伐强度时得到的R2的最小值、最大值和极差可以看出,不同采伐强度时同一树高曲线得到的R2值相差较大,说明同一树高曲线对于不同采伐强度时的树高预测精度相差较大。比较表6中同一采伐强度时10 个树高曲线模型的R2的最小值、最大值和极差可以看出,同一采伐强度时10 个树高曲线的R2的最小值和最大值相差也较大,说明采伐强度一定时,不同的树高曲线模型预测精度相差也较大。比较表5和表6中R2的标准差可以看出,同一树高曲线在不同采伐强度时获得的R2的离散性(R2的标准差都在0.17 左右),较同一采伐强度时不同树高曲线获得的R2的离散性(R2的标准差大多在0.05 以下,仅有一种情况为0.148)大,说明采伐强度是影响树高曲线模型选择的重要因素。综上所述,对于不同的采伐强度,可通过选取合适的树高曲线模型增加树高的预测精度。
按照R2较大、Mse及Sse较小的原则,对表4中每一采伐强度的10 种树高曲线模型进行对比分析,得出18 块样地的最优曲线模型及与最优曲线模型相近的模型(见表7)。从表7可看出,不同采伐强度的树高曲线模型的选择性。
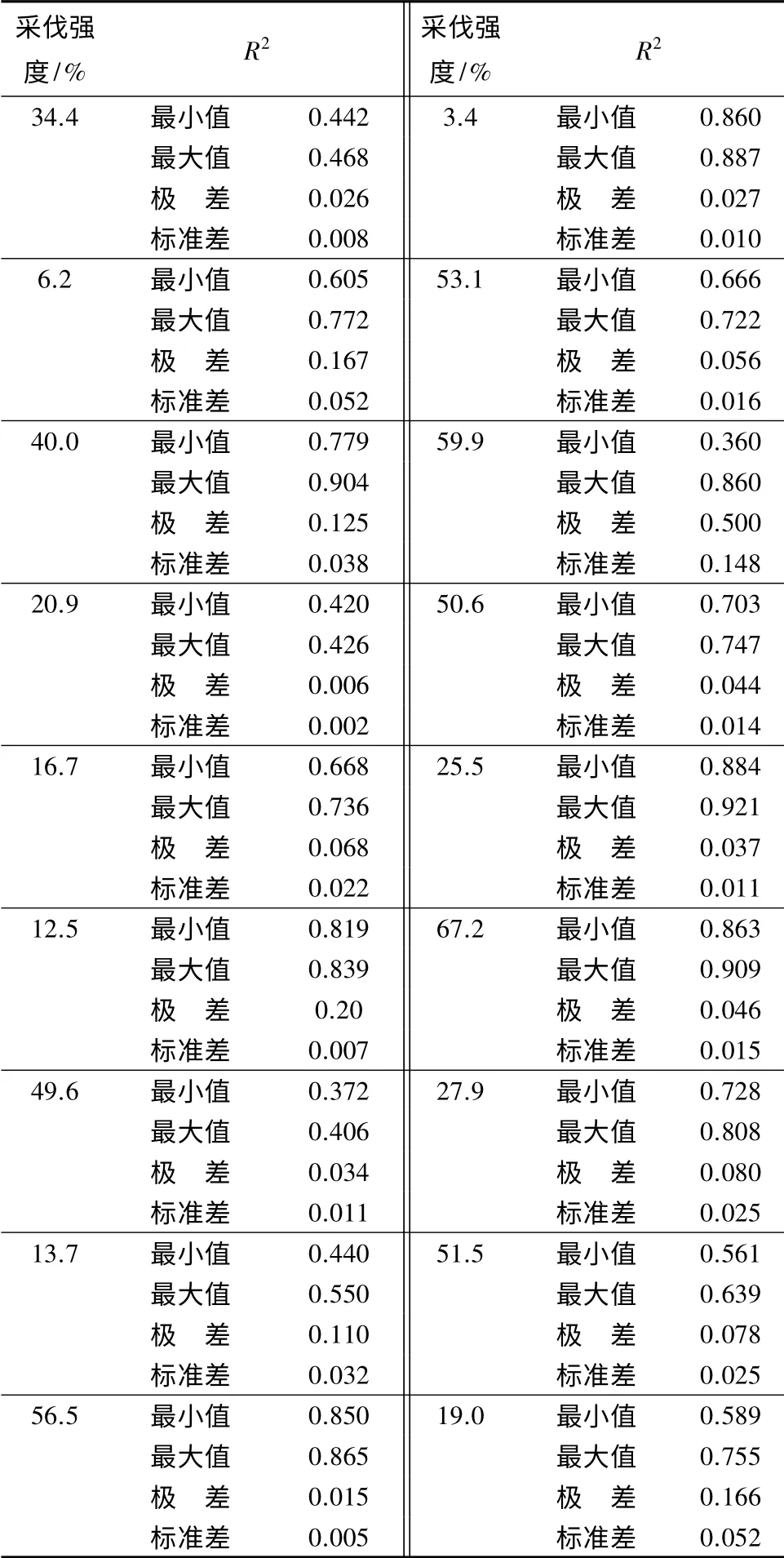
表6 同一采伐强度、不同树高曲线的R2
4 结论与讨论
本文对大兴安岭落叶松在不同采伐强度时的树高曲线模型进行了研究。选择了18 块采伐强度不同的样地,应用激光测距仪和胸径围尺测量了树高和胸径数据,以10 种常用的树高曲线模型作为候选模型。通过比较同一采伐强度时不同树高曲线获得的R2,结果表明:每一种采伐强度获得的R2的最大值和最小值差值较大,有11 块样地的差值超过了0.04;最大差值达到了0.5;且每一种采伐强度的R2的最大值均超过了0.4,其中有14 块样地的R2的最大值超过了0.64,8 块样地的R2的最大值超过了0.8。由此可见,采伐强度一定时,通过选择最优树高曲线模型可以显著提高树高的预测精度;文中选用的10 种候选模型能够满足大兴安岭落叶松在不同采伐强度时树高的预测需要。
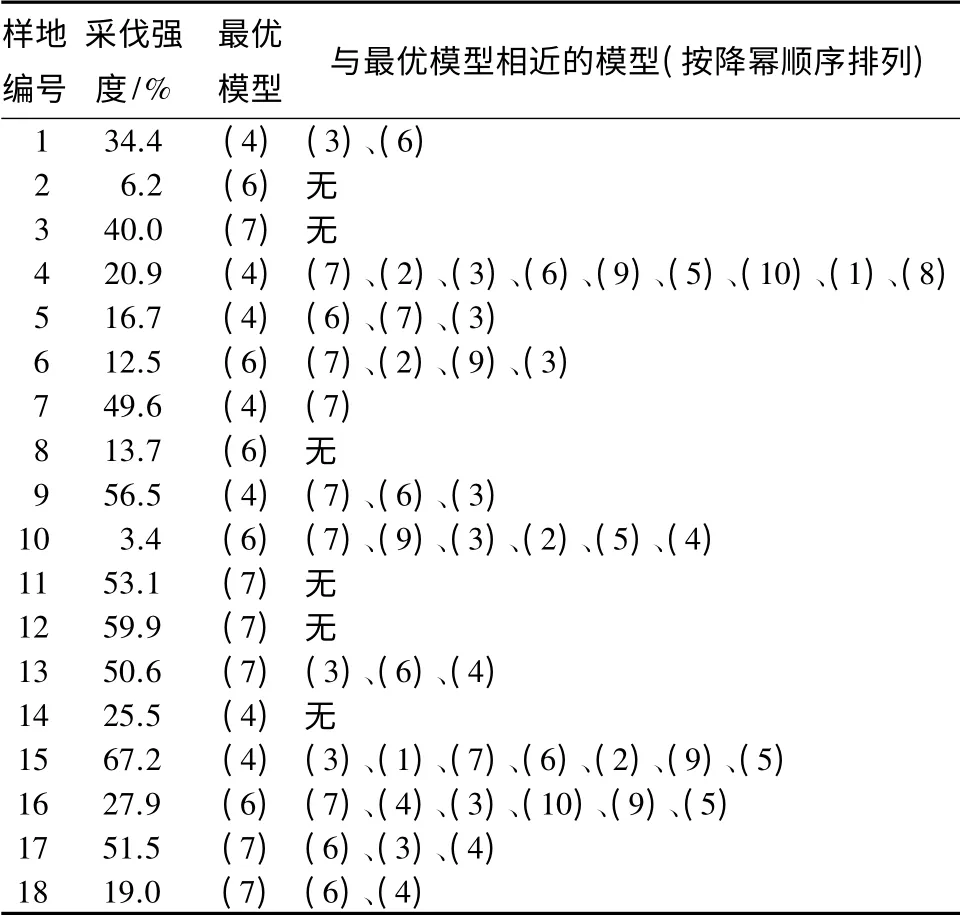
表7 最优模型及与最优模型相近的模型
通过对比同一树高曲线、不同采伐强度时获得的R2,结果表明:同一树高曲线在不同采伐强度时获得的R2的离散性较大(R2的极差达到了0.50 左右,R2的标准差为0.17 左右)。由此说明,同一树高曲线模型对于不同采伐强度的树高预测精度相差较大。可见,为了提高大兴安岭落叶松在不同采伐强度时的树高预测精度,需要针对采伐强度的强弱选择合适的树高曲线模型,目前还没有关于这方面的研究。以往研究中,为了提高树高的预测精度,学者更多的是致力于在模型中引入新的变量[19-21],并没有针对不同采伐强度选用不同树高曲线模型的研究。
以R2、Sse、Mse作为模型优劣的评价指标,对18块样地的最优模型及与最优模型相近的模型进行整理(见表7),结果表明:采伐强度为34.4%、20.9%、16.7%、25.5%、49.6%、56.5%和67.2%时,最优模型为模型(4);采伐强度为6.2%、12.5%、13.7%、3.4%和27.9%时,最优模型为模型(6);采伐强度为40.0%、53.1%、59.9%、50.6%、51.5%和19.0%时,最优模型为模型(7)。可见,大兴安岭落叶松在不同采伐强度时对应的最优树高曲线模型主要有3 个,即Logistic 模型(模型(4))、Richard 模型(模型(6))、Weibull 模型(模型(7))。为了方便其它采伐强度时能够选择出合适的树高曲线模型,对模型(4)、模型(6)、模型(7)对应的采伐强度情况进行对比分析。观察表8中不同采伐强度时的最优模型及与最优模型接近的模型可以看出,模型(7)主要适宜强采伐强度(采伐强度在40%及以上)时的树高预测,其中,对于采伐强度为49.6%、56.5%和67.2%时,模型(7)虽然不是最优模型,但从表8中的与最优模型相近的模型可以看出,对于这3 种采伐强度时,模型(7)均与其对应的最优模型(4)接近(49.6%采伐强度时,最优模型(4)的R2为0.406,模型(7)的R2为0.395;56.5%采伐强度时,最优模型(4)的R2为0.865,模型(7)的R2为0.862;67.2%采伐强度时,最优模型(4)的R2为0.909,模型(7)的R2为0.904);模型(6)主要适宜低采伐强度(采伐强度在15%以下)时的树高预测;模型(4)主要适宜中等采伐强度(采伐强度在15%~40%)时的树高预测,对于采伐强度为19.0%和27.9%时,模型(4)虽然不是最优模型,但从表8中的与最优模型相近的模型可以看出,对于这2 种采伐强度下的采伐,模型(4)同样与其对应的最优模型接近(19.0%采伐强度时,最优模型(7)的R2为0.755,模型(4)的R2为0.751;27.9%采伐强度时,最优模型(6)的R2为0.808,模型(4)的R2为0.807)。综上所述,大兴安岭落叶松在采伐强度较低(低于15%)时,较适合的树高曲线模型为Richard(1959)模型;采伐强度在15%~40%时,较适合的模型为Logistic 模型;采伐强度为40%及以上时,较适合的模型为Weibull(1978)模型。比较3 个模型可以看出,3 个模型均为3 参数的模型。
本文在不增加树高曲线模型变量的情况下,采用针对不同采伐强度选用不同树高曲线模型的方法,提高了树高的预测精度,方法更简单,更实用。本文仅针对大兴安岭落叶松在不同采伐强度时的树高曲线模型进行了研究,给出了大兴安岭落叶松在弱度采伐、中度采伐、强度采伐时分别适合的模型。对于其他树种,采伐强度是否对其树高预测有明显的影响,每一种树种在采伐强度不同时应选择什么样的树高曲线模型,还有待进一步的研究。
[1] 刘发林,吕勇,曾思齐.森林测树仪器使用现状与研究展望[J].林业资源管理,2011(1):96-99.
[2] 隋宏大.树高测量综合技术比较研究[D].北京:北京林业大学,2009.
[3] Wykoff W R,Crookston N L,Stage A R.User’s guide to the stand prognosis model[M].Washington D C:USDA Forest Service,1982.
[4] Curtis R O.Heigh-diameter and heigh-diameter-age equations for second-growth Douglas-fir[J].Forest Science,1967,13(4):365-375.
[5] Authors Sweda T,Umemura T.TitleA theoretical height-diameter curve(I):derivation and characteristics[J].JournalJournal of the Japanese Forestry Society,1980,62(12):459-464.
[6] Huang Shongming,Titus S J,Wiens D P.Comparison of nonlinear height-diameter functions for major Alberta tree species[J].Canadian Journal of Forest Research,1992,22(9):1297-1304.
[7] Calama Rafael,Montero Gregorio.Interregional nonlinear height-diameter model with random coefficients for stone pine in Spain[J].Canadian Journal of Forest Research,2004,34(1):150-163.
[8] Huang Shongming,Meng Shawn X,Yang Yuqing.Using nonlinear mixed model technique to determine the optimal tree height prediction model for black spruce[J].Modern Applied Science,2009,3(4):3-18.
[9] Adame P,Río M D,Caellas I.A mixed nonlinear height-diameter model for pyrenean oak (Quercus pyrenaica Willd)[J].Forest Ecology and Management,2008,256(1/2):88-98.
[10] 王明亮,李希菲.非线性树高曲线模型的研究[J].林业科学研究,2000,13(1):75-79.
[11] 郑扬,骆崇云,栗生枝.辽宁省东部山区主要针叶树种最优树高曲线研究[J].山东林业科技,2014(3):11-16.
[12] 魏京.林木胸径与树高的关系研究[J].湖北民族学院学报:自然科学版,2014,32(2):190-192.
[13] 曾翀,雷相东,刘宪钊,等.落叶松云冷杉林单木树高曲线的研究[J].林业科学研究,2009,(2):182-189.
[14] 王小明,李凤日,贾炜玮,等.帽儿山林场天然次生林阔叶树种树高-胸径模型[J].东北林业大学学报,2013,41(12):116-120.
[15] 张敏,顾凤歧,董希斌.帽儿山林区主要树种树高与胸径之间的关系分析[J].森林工程,2014,30(6):1-4.
[16] 白艳.不同采伐方式对兴安落叶松林分特征及其植物多样性的影响[D].呼和浩特:内蒙古农业大学,2012.
[17] 韦雪花,王佳,冯仲科.北京市13 个常见树种胸径估测研究[J].北京林业大学学报,2013,35(5):56-63.
[18] 赵俊卉,亢新刚,刘燕.长白山主要针叶树种最优树高曲线研究[J].北京林业大学学报,2009,31(4):13-18.
[19] Sánchez-González M,Ca~nellas I,Montero G.Generalized heightdiameter and crown diameter predictionm odels for cork oak forestsin Spain[J].Sistemasy Recursos Forestales,2007,16(1):76-88.
[20] Misir N.Generalized height-diameter models for Populus tremula L.stands[J].African Journal of Biotechnology,2010,9(28):4348-4355.
[21] Krisnawati H,Wang Y,Ades P K.Generalized heightdiameter models for Acacia mangium Willd plantations in south Sumatra[J].Journal of Forestry Research,2010,7(1):1-19.

