土壤养分因子对蒙古栎林优势木生长的影响1)

王岳 王海燕 李旭 何丽鸿 李卫松

(北京林业大学，北京，100083)

责任编辑:潘 华。

林分优势木树高、胸径调查是表征该林分生产潜力的重要数据来源。有研究表明，优势木的树高与林分密度及间伐强度关系不大［1－3］，因此，立地条件和气候因子就成为其主要影响因素。基准年龄下优势木的平均高，即地位指数，常被用来反映立地生产力的大小，且因其调查方法相对简单而得到了广泛应用，但此方法不能完全说明立地条件的复杂特征，尤其是土壤因子对优势木生长的影响。此外，随着直径生长模型研究的深入［4－5］，运用胸径、树高、材积共同表征林分内树木的生长情况更加系统和科学。不同林分条件下的树高—胸径曲线，不论是普通树高曲线还是标准树高曲线，均以林分因子如树高、胸径、优势木平均高、优势木平均胸径、林分公顷断面积等作为模型变量［6－8］。模型的类型也有较新变化，如符利勇等［9］、李春明等［10］利用非线性混合模型对杉木优势木平均高进行了研究，赖巧玲等［11］则应用非参数估计构造树高曲线，这些变量易于测量和计算，拟合效果好且对生产具有实际指导意义，但立地条件中土壤因子对树高—胸径曲线中变量的影响却鲜有研究。

蒙古栎(Quercus mongolica)是我国落叶栎中分布最北的一个种，是营造防风林、水源涵养林及防火林的优良树种，同时也是落叶栎类中抗逆性较强的树种之一。它是我国东北地区针阔混交林的主要建群种，具有重要的生态价值和经济价值［12］，在维持地域生态平衡和生态系统恢复重建中起到重要作用。本文以吉林汪清林业局塔子沟林场蒙古栎林为对象，通过测树因子调查和土样测定分析，探讨了土壤养分因子对蒙古栎林优势木生长的影响，以期为该区域森林经营管理提供依据。

1 研究区概况

研究区位于吉林省汪清林业局塔子沟林场(129°56'～131°04'E，43°05'～43°40'N)，属山地丘陵地带，温带大陆性季风气候，年平均气温3.9 ℃，年平均降水量547 mm。在林场范围内选取12 块1 hm2大样地，样地是以蒙古栎为主要建群种的蒙古栎阔叶混交林，阔叶树种有水曲柳(Fraxinus mandshurica)、白桦(Betula platyphylla)、紫椴(Tilia amurensis)、枫桦(Betula costata)、榆树(Ulmus propinqua)等。林下植被丰富，灌木主要有瑞香(Daphne koreanum Nakai)、稠李(Prunus padus)、刺玫蔷薇(Rose dahurica)等30 余种，草本主要有艾蒿(Artemisia vulgaris)、白花碎米荠(Cardamine leucantha)、白屈菜(Chelidonium majus)等200 余种。土壤类型以暗棕壤为主。

2 研究方法

2.1 样地设置

在12 块1 hm2大样地中，以20 m×100 m 共设置60 块样地，并将其平均分为20 个10 m×10 m 样方，每个样方内采集0～20 cm 土样并充分混合，得到60 个混合土样。根据相关技术规定［13］测量样地内蒙古栎树高和胸径，选取5 株最高木作为优势木。

2.2 树木材积的计算

根据GB 4814—84 中的计算公式(当D＞14 cm，V=0.785 4L［D+0.5L+0.005L2+0.000 125L(14－L)2(D－10)］2/10 000;当2＜D＜14 cm，V=0.785 4L(D+0.45L+0.2)2/10 000，其中D 为胸径，L 为树高，V 为材积)计算蒙古栎材积。

2.3 土壤养分因子的测定

测定混合土样中有机质—外加热重铬酸钾氧化—容量法;全磷—硫酸—高氯酸消煮—钼锑抗比色法;全钾—氢氟酸—高氯酸消煮—火焰光度计法;全氮—硫酸—高氯酸消煮—凯氏定氮仪法;有效磷—氟化铵—盐酸—钼锑抗比色法;速效钾—中性乙酸铵浸提—火焰光度计法;土壤pH 值—酸度计法(V(水)∶V(土)=2.5 ∶1.0)［14］。

2.4 数据处理

应用Excel 2010 和SPSS 18.0 对数据进行分析。利用Pearson 相关系数表征两变量间的线性相关程度。

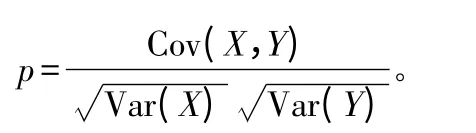
式中，Cov(X，Y)是随机变量X 和Y 的协方差;Var(X)和Var(Y)分别为变量X 和Y 的方差。

选取显著相关变量，运用常用的6 种曲线模型对林分测树因子与土壤变量进行拟合(表1)，并采用多元线性逐步回归方法分析模型中土壤因子的组成。

表1 曲线模型方程

3 结果与分析

60 块20 m×100 m 样地的土壤养分质量分数及优势木调查数据见表2。样地均符合材积计算公式要求，数据具有代表性。

表2 土壤养分质量分数及优势木树高、胸径统计

续(表2)

对表2中土壤变量及优势木指标进行相关性分析，各变量间相关系数及显著性见表3。由表3可以看出，优势木平均胸径和树高之间并没有显著相关关系，而与土壤pH 值、有效磷及全钾质量分数显著相关。将优势木平均胸径分别与土壤pH 值、有效磷和全钾质量分数进行拟合，得到参数检验与模型检验均显著且拟合优度(调整R2)最高分别是“S”形曲线、“S”形曲线和Logistic 曲线(表4)。由图1和图2可以看出，虽然同为“S”形曲线，但样地间土壤pH 值差异并不大，这说明样地内优势木平均胸径与土壤pH 值之间的显著相关性实际上是通过影响样地内其他元素的质量分数来体现。因此，用土壤pH 值与优势木的数据进行模型拟合并不能反映出pH 值对树木生长的影响。

续(表3)

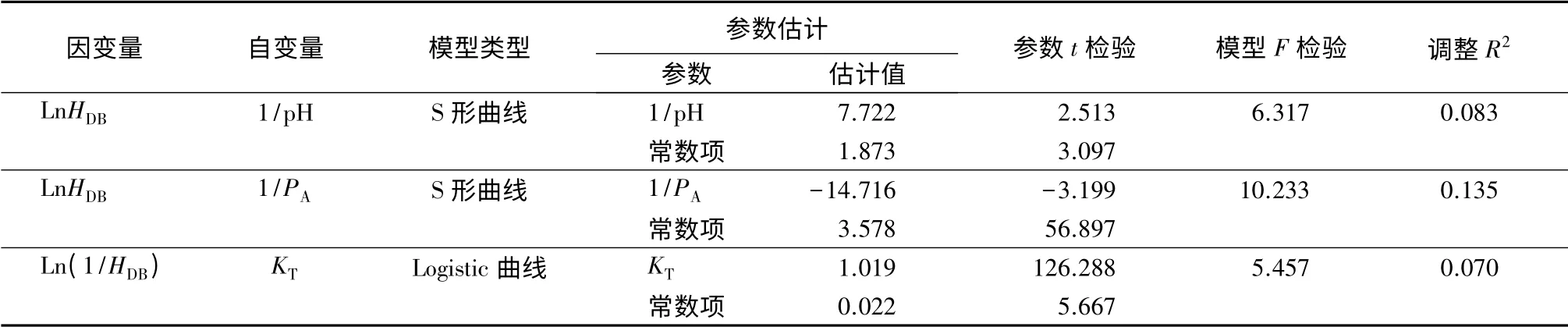
表4 曲线回归分析参数估计

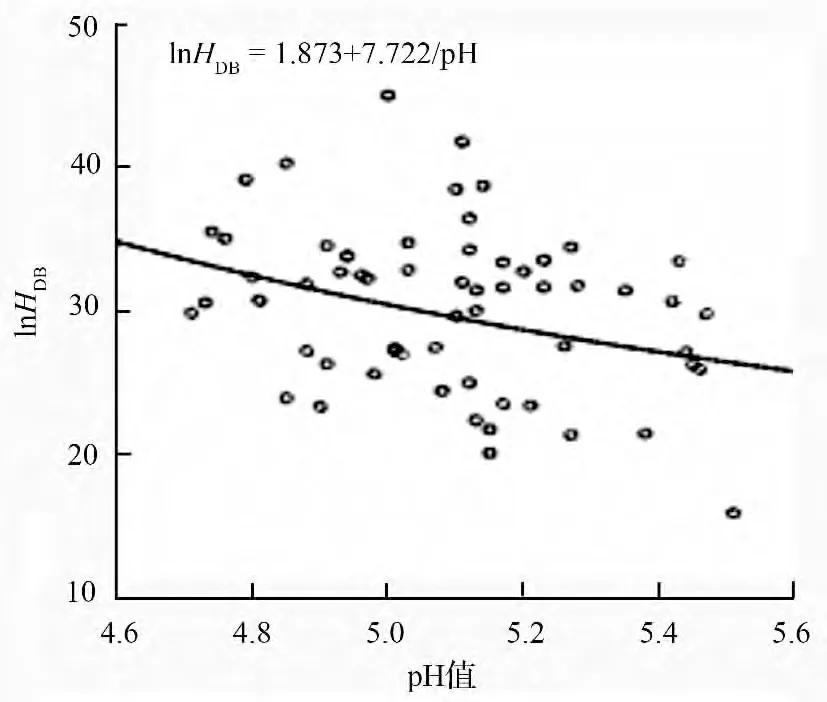
图1 胸径与土壤pH 值“S”形曲线

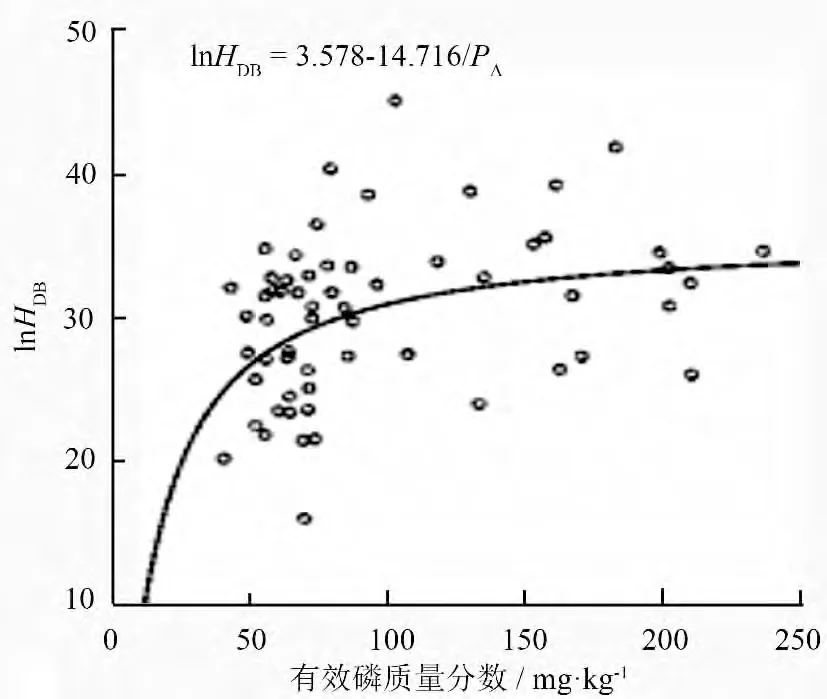
图2 胸径与土壤有效磷“S”形曲线

图3 胸径与土壤全钾“Logistic”曲线

将优势木平均胸径与这3 个土壤因子进行多元线性回归分析(表5)。

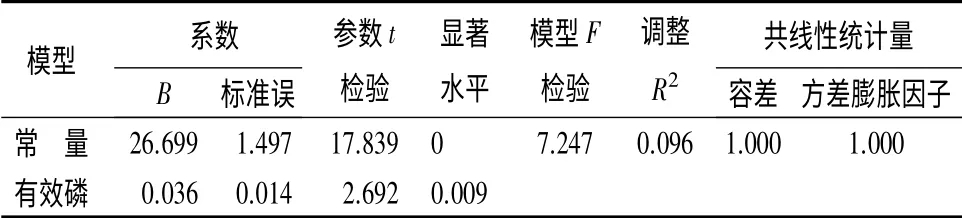
表5 多元线性回归参数

发现仅土壤有效磷质量分数进入模型HDB=26.70+0.036PA。由此方程可以得出，当胸径大于27 cm 时，虽然优势木平均胸径仍随土壤有效磷质量分数的增加而增加，但其增幅明显降低，即土壤有效磷质量分数对胸径的影响明显减小。当胸径达到27 cm 时曲线的斜率明显降低，这与二者曲线模型拟合结果相一致(图1—图3)。

4 结论与讨论

土壤因子对立地生产力有显著影响，作为立地条件的重要组成部分，土壤养分因子对优势木平均胸径影响显著，虽然土壤物理性质对土壤养分有效性及根系分布有一定影响，但不论是曲线回归还是多元线性回归，最终进入模型的土壤变量都是土壤养分因子。相关分析结果表明，优势木树高、胸径间无显著相关关系。但本文分析只针对优势木，不能说明全林分条件下胸径、树高之间不存在显著相关关系。

以往的树高—胸径曲线是基于样地内调查的全部树木数据进行分析和模型检验，因此曲线的拟合效果较好［15－16］。本研究中优势木树高和胸径并没有呈现显著线性相关，说明在树木生长过程中胸径随树高的变化并不能够用简单的线性关系描述［17］，对于不同树种，曲线模型的精度也达不到要求，因此混合模型得到应用［18］。不同生长阶段树高、胸径关系发生变化的原因可能是在成为种群中优势个体之后，由于树高较高，对于林分内各个因子的争夺也处在相对优势的地位，并不需要通过植株的增粗对其进行保护。

土壤pH 值影响树木生长主要表现在两个方面，一是影响植物根系生长，二是影响土壤养分的有效性。随着土层加深，土壤pH 值有增大的趋势，但作为土壤养分因子中变异系数最小的因子［19－20］，不同样地间同一土层的土壤pH 值差异不大，即使样地表层土壤间pH 值略有不同，pH 值也不能作为数值型变量与其他土壤因子一起与因变量进行模型拟合，其主要作用是判断土壤基本性质或是分析不同层次间土壤pH 与养分吸收的关系。因此，优势木平均胸径虽然与土壤pH 值有显著相关关系，但这种相关性的本质是pH 值对树木吸收养分的影响。

对样地内优势木平均胸径与土壤因子的多元线性回归分析，最终进入模型的仅土壤有效磷。土壤养分全量与有效量一直是土壤测定分析的重要指标，全量表征的是土壤支持林分生长的潜力，而实际为树木生长提供营养元素的是土壤中元素的有效量。由于表层土壤枯落物较多，促进枯落物及有机质分解的微生物的活动相对频繁，表层土壤的元素有效量对植物生长的作用更加重要。P 元素作为植物所需大量营养元素，是细胞中磷脂、核酸、核蛋白等化合物的组成成分，参与脂肪代谢及碳水化合物的代谢和运输，对植物生长具有重要意义。由于一般树木的生长，在幼龄时树高生长明显，表现为树高的速生期，但生长到一定高度时，生长减慢，而径生长加快，表现为胸径生长的速生期，因此在胸径生长旺盛时期有效磷浓度对其影响较小，即为图2表现出的斜率显著降低，P 元素对植物光合作用影响较大，在以营养生长为主的中、幼龄时期，作为细胞分裂原料的核酸、核蛋白等对树木生长影响较大，宏观上同样表现为P 元素对树高生长的影响。

本研究中，优势木对于土壤因子的响应并不十分显著，原因可能是当树高达到一定高度时，树木根系的生长也相对发达，整体对于土壤养分的吸收处于优势地位，此时，光照、温度和水分等气候因子成为影响树木生长的主要因子，这也是优势木在自然条件下不易枯死的原因。图3反映出的优势木平均胸径随土壤全钾浓度升高而降低的趋势不符合大量营养元素对植物生长的影响规律，具体原因还需要进一步研究。虽然土壤因子与立地指数相关性不显著，与优势木平均胸径的各模型的拟合优度不高，但综合树木生长规律，土壤仍然是重要的立地因子之一。今后，可以运用相对灵活的模型，通过不同算法间的转化及函数变量的适当变形，使得土壤因子与优势木林分因子的拟合效果更好，还可利用径阶等分类原理分别探究土壤养分浓度对不同树高范围和胸径的影响。

［1］ Wang M L，Borders B E，Zhao D H.Parameter estimation of based-age invariant site index models:which date structure tousereply［J］.Forestry Science，2008，54(2):129－133.

［2］ Fang Z X，Bailey R L.Nonlinear missed effects modeling for slash pine dominant height growth following intensive silvicultural treatments［J］.Forestry Science，2001，47(3):287－300.

［3］ 相聪伟，张建国，段爱国.山地杉木人工林优势木选择方法的研究［J］.西北农林科技大学学报:自然科学版，2012，40(9):51－53.

［4］ Trasobares A，Pukkala T.Using past growth to improve individualtree diameter growth models for uneven-aged mixtures of Pinus sylvestris L.and Pinus nigra Arn.in Catalonia，north-east Spain［J］.Annals of Forest Science，2004，61(5):409－417.

［5］ Pukkala T，Lahde E，Laiho O.Growth and yield models for uneven-sized forest stands in Finland［J］.Forest Ecology and Management，2009，258(3):207－216.

［6］ 胥辉，全宏波，王斌.思茅松标准树高曲线的研究［J］.西南林学院学报，2000，20(2):74－77.

［7］ Adame P，Rio M D，Canellas I.A mixed nonlinear height-diameter model for Pyrenean oak(Quercus pyrenaica Willd.)［J］.Forest Ecology and Management，2008，256(1/2):88－98.

［8］ Sharma M，Parton J.Height-diameter equations for boreal tree species in Ontario using a mixed-effects modeling approach［J］.Forest Ecology and Management，2007，249:187－198.

［9］ 符利勇，张会儒，唐守正.基于非线性混合模型的杉木优势木平均高［J］.林业科学，2012，48(7):66－72.

［10］ 李春明，张会儒.利用非线性混合模型模拟杉木林优势木平均高［J］.林业科学，2010，46(3):89－95.

［11］ 赖巧玲，胥辉，杨为民.非参数估计在构造树高曲线中的应用［J］.北京林业大学学报，2006，28(4):77－81.

［12］ 李文英，顾万春.蒙古栎天然群体表型多样性研究［J］.林业科学，2005:41(1):49－57.

［13］ 中华人民共和国林业部.林业专业调查主要技术规定［M］.北京:中国林业出版社，1990.

［14］ 鲍士旦.土壤农化分析［M］.3 版.北京:中国农业出版社，2000.

［15］ 王明亮，唐守正.标准树高曲线的研制［J］，林业科学研究，1997，10(3):259－264.

［16］ Temesgen H，Gadow K V.Generalized height-diameter models:an application for major tree species in complex stands of interior British Columbia［J］.European Journal of Forest Research，2004，123(1):45－51.

［17］ 李海奎，法蕾.基于分级的全国主要树种树高:胸径曲线模型［J］.林业科学，2011，48(10):83－91.

［18］ Meng S X，Huang S，Lieffers V J.Wind speed and crown class influence the height-diameter relationship of lodgepole pine:nonlinear mixed effects modeling［J］.Forest Ecology and Management，2008，256(4):570－577.

［19］ 杨晓娟.东北长白山系低山丘陵区不同林分土壤肥力质量研究［D］.北京:北京林业大学，2013.

［20］ 任丽娜，王海燕，丁国栋，等.华北土石山区人工林土壤健康评价研究［J］.水土保持学报，2010，24(6):46－52.