纵边支承柱面网壳抗震方案及参数分析比较
周海涛,张毅刚,吴金志
(1. 河南城建学院,河南 平顶山467036;2.北京工业大学 空间结构研究中心,北京100124;3. 北京工业大学 城市与工程安全减灾省部共建教育部重点实验室,北京100124)
图7 不同屋面荷载作用下峰值加速度-用钢量增加比例关系曲线
图8 不同矢跨比峰值加速度-用钢量增加比例关系曲线
纵边支承柱面网壳抗震方案及参数分析比较
周海涛1,2,张毅刚2,3,吴金志2
(1. 河南城建学院,河南 平顶山467036;2.北京工业大学 空间结构研究中心,北京100124;3. 北京工业大学 城市与工程安全减灾省部共建教育部重点实验室,北京100124)
以第一斜杆断裂带生成为结构倒塌标准,以其对应结构峰值加速度为抗震能力指标,计算分析了7个提高结构抗震能力的方案的力学表现,证明在相同用钢量增加比例的情况下,增强横杆截面方案比增强斜杆截面方案更为合理,进一步计算表明屋面重力荷载,矢跨比对结构抗震性能有明显影响。随其变化各方案的费效比表现各异,针对各具体情况,并兼顾用钢量,分别提出了较优方案,对具体工程有一定示范和启发意义。
单层柱面网壳;抗震能力指标;抗震方案比较;损伤集中现象;
网壳结构以其形体优美简洁、经济合理等优点在航站楼、火车站、体育馆、大型厂房等大跨空间领域得到广泛应用。这类建筑除实现日常大量人员、物资设备的容纳使用功能外,还要在各种严重自然灾害发生后作为公共灾民临时安置中心或救灾物资设备协调集散中心使用。如果在强震条件下发生倒塌,往往会导致惨重的人员伤亡和财产损失,因此网壳结构设计重要性级别往往定为甲级,且针对其强震下抗倒塌的措施研究已进入学界的研究领域。
规范规定,对于甲类建筑,设防烈度为9度(约400 gal)时,应符合比9 度抗震设防更高的要求[1]。除了目前15个9度设防地级市外[2],可以预期,随着国民经济水平的进一步提高,还会有更多地区将目前的抗震设防烈度从8度调至9度。对于灾后重建区域,有学者提议设防烈度宜取9度,这意味着对于越来越多的甲类建筑设防烈度应该超过400 gal,而大量计算表明,对于矢跨比较高或者屋面重力荷载较大的纵边支承单层柱面网壳,极可能在峰值加速度为400 gal的强震作用下完全倒塌。因此网壳结构9度及9度以上强震条件下的抗倒塌研究有着重要的现实工程意义。
目前针对空间结构的抗震方法大致分为以下两类:一类是进行振动控制[3],由控制机构和结构共同承受地震作用,共同储存和消耗地震能量,以协调和减轻结构的反应,即隔振减震。这方面研究内容较多,但是存在着诸如各类控制机构在结构分析中的数值模拟方法、设置位置与数目的优化考虑等难题[4],且对于体量中等的柱面网壳,施工费用及震后修复费用问题也较突出。另一类则是通过加大构件截面尺寸,改变局部构件几何形式等方法来提高结构刚度,增强抗震能力,该类方法理论简单,易于进行数值模拟,有利于设计计算,因此被广泛应用。但是,针对纵边支承柱面网壳,不同构件加强方案的抗震效果定量计算,各方案之间的经济性比较,最优方案的选择判断,各方案在不同矢跨比、不同重力荷载作用条件下对结构抗震能力的影响特征等方面的问题,目前尚无文献进行分析以供设计者参考。
本文基于不同的抗震原理分别研究了两大类,共6个不同的杆件处理方式对结构抗震性能的影响,并进行经济性比较,同时兼顾静力极限承载力,得出了较好的提高网壳抗震性能的措施,并进行了参数分析。
1 抗震能力指标
新抗震规范中的“大震不倒”原则在柱面网壳方面的具体解释依然模糊,没有给出“倒”的具体定义,而文献[5]通过对大量纵边支承柱面网壳算例倒塌过程的仿真分析认为,纵边支承柱面网壳倒塌过程存在“双-斜杆断裂带”模式,即强震条件下柱壳在横向1/4处和跨中先后形成两条斜杆断裂带(见图1),并且最终结构整体坍塌成“M”状。这两条斜杆断裂带位置随结构几何尺寸变化而稍有变化。
根据工程适用性要求,强震下当第一条斜杆断裂带生成后(见图2),即可认为柱壳结构失去使用价值,因此本文提出,当第一条斜杆断裂带生成时即可认为纵边支承柱面网壳结构发生“倒”塌破坏。
由此,以一定地震计算时长结束时形成第一条斜杆断裂带所对应的地震波加速度峰值作为结构的抗震能力指标是合适的。文献[6]中关于大跨结构部分的条文规定计算时长大于自振周期10倍即可。基于此项规定并参考诸多文献算例,本文采用18 s为标准时长。
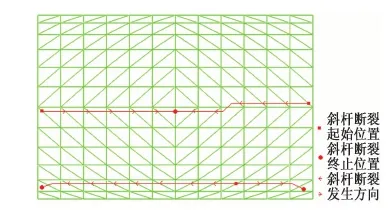
图1 纵边支承柱面网壳倒塌模式示意图
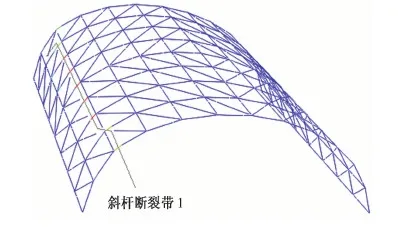
图2 第一斜杆断裂带形态示意图
2 标准模型及抗震方案
以图3所示的典型单层纵边支承单斜杆柱面网壳为标准分析模型,长度30 m,跨度20 m,矢高7.5 m,纵边节点落地铰接,屋面重力荷载1.5 kN/m2,使用3D3S进行设计并参考工程做法,横向杆件和斜杆截面均为Ø146×5热轧钢管,纵杆为Ø88×4热轧钢管,所有杆件均划分为等长度四单元,每个单元截面划分为8根等尺寸纤维。
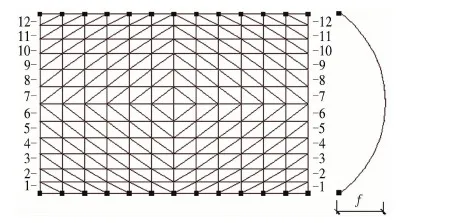
图3 柱壳模型
首先施加重力荷载算得结构震前初始力学特征参数,然后进行动力弹塑性计算,在网壳支座处施加三向Taft波,地震波峰值比例为1∶0.85∶0.65,X方向为网壳横向。考虑几何非线性和材料非线性,材料本构为考虑损伤累积效应的混合硬化材料模型,模型中各材料模量均为考虑了性能劣化效应的有效模量,算得18 s时结构倒塌对应地震动加速度峰值为395 gal。
根据工程中可实现做法,为实现加速度为400~800 gal时结构的安全性,保证“大震不倒”,如表1所示,共选取了6个代表性抗倒塌方案。
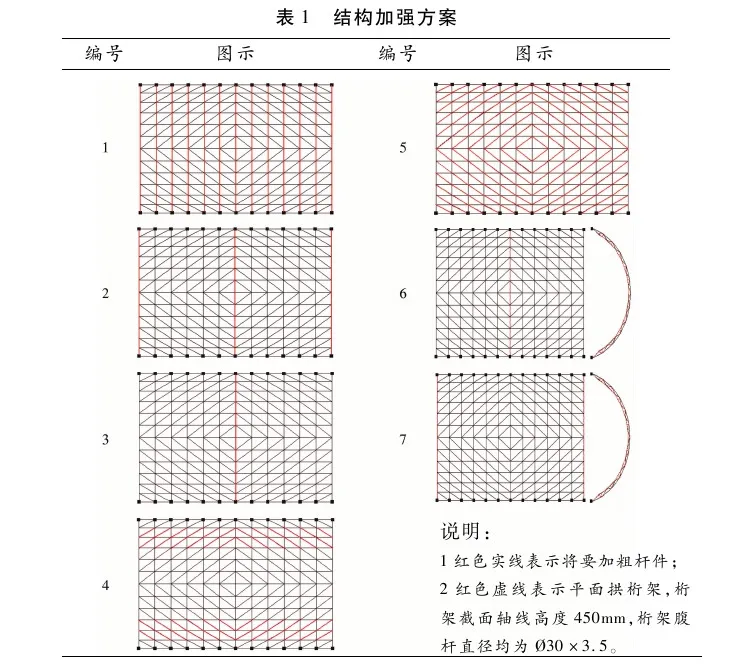
方案1在标准模型基础上等幅加粗所有横杆;方案2加粗中间和两端共3根横杆;方案3仅加粗最中间横杆;方案4 则把2-2,3-3节间及对称的10-10,11-11节间斜杆等幅加粗;方案5把所有斜杆等幅加粗;方案6和方案7则分别在中间榀横杆与两端横杆下方增设腹杆与下弦杆,使对应横杆成为平面拱桁架,除下弦杆外,其他杆件截面和桁架高度均为恒定。各方案中加粗的钢管截面尺寸参数均来源于GBT 17395-1998,且壁厚始终为6 mm。
方案1~3、方案6~7的抗震机理是通过增强结构的横向刚度,限制结构在强震条件下的侧向变形,尤其是塑性变形,延迟或避免因损伤在网壳一侧集中发展,相应延迟或避免第一斜杆断裂带过早形成,达到提高结构抗震能力。方案4则通过直接提高斜杆断裂带处斜杆横截面以期延缓斜杆过早破坏,方案5则希望增大断裂带处斜杆截面的同时也能增强结构的侧向刚度。
3 计算结果分析
经过大量计算,以用钢量增加比例为横轴,结构在18 s时倒塌对应峰值加速度及屈曲荷载系数为纵轴,得出图4和图5。
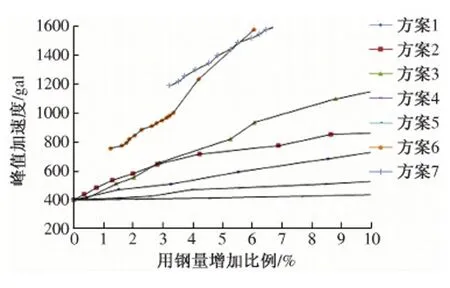
图4 倒塌峰值加速度—用钢量增加比例关系曲线
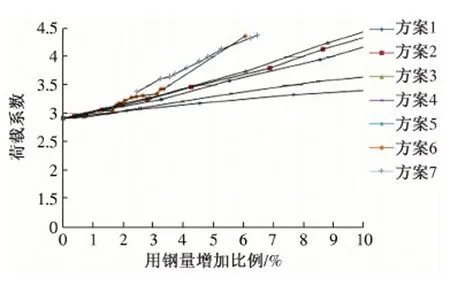
图5 荷载系数—用钢量增加比例关系曲线
分析图4可知:
(1)随着用钢量增加比例的提升,方案6、方案7的结构抗震能力指标增加最为迅速,方案1、方案2次之,方案4和方案5最差。结构的静态极限承载力发展有着相同的趋势,如图5所示。这说明增强结构抗震能力的决定因素是截面增强方式。很显然,增大斜杆截面是费效比最差的。由于平面拱桁架腹杆及隅撑的存在,方案6和方案7初始用钢量增加比例不为0。
(2)通过曲线的斜率的大小对比关系可知,在相同用钢量增量情况下,整体上方案3对结构抗震能力的提高效果要优于方案2,方案2又优于方案1,表明把用钢增量集中在局部横杆截面上可以取得较平均分配更好的费效比。把各方案在同一用钢增量条件下所有横杆截面的抗弯模量和抗剪模量进行累加计算并比较,存在方案3稍大于方案2,方案2明显大于方案1的关系,故整体结构横向刚度必然存在相应对比关系。较大的横向刚度能更好地限制结构侧向变形,因此能较好地推迟结构损伤在第一斜杆断裂带上出现。
(3)当用钢量增加小于2.8%时,方案2抗震能力要稍大于方案3。
这是因为横杆截面几何尺寸的不均匀性导致结构损伤分布的不均匀性,得到加强的中间横杆及该横杆相邻斜杆材料在地震中经受更大的内力而更容易发生损伤,如图6所示,且分布的不均匀性随横杆几何尺寸不均匀性的加剧而加剧,本文称之为损伤集中效应。当杆件截面增加有限,刚度增加不大时,这种效应的影响相对明显,会削弱横杆加强对结构刚度的增强效果。但随着横杆截面的增大,相对于截面增大带来的结构刚度的提高将明显超过横杆损伤集中效应引起的刚度劣化,并掩盖后者的影响。因此在本算例中,当用钢量增加大于2.8%时,方案3要比方案1有更好的费效比。图5中极限承载力曲线则没有体现出这一特征。
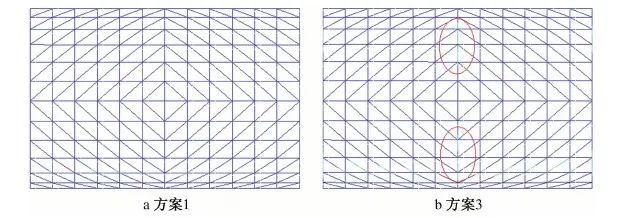
图6杆件损伤分布示意图
(4)表2显示随斜杆截面增大,方案4和方案5结构抗震能力相应增强,但可以发现在采用同样增大斜杆截面,耗用了更多钢材的情况下,方案5的抗震能力反比方案4要差,这是因为对于方案5,虽然更多的斜杆用钢量理论上可以延迟斜杆的损伤和断裂并一定程度上增强结构刚度,但是由于提高程度极有限,而结构自重却增加很多,使得地震动作用下结构构件内力过大,反而促进了结构的倒塌,导致结构抗震能力相比方案4有所下降。
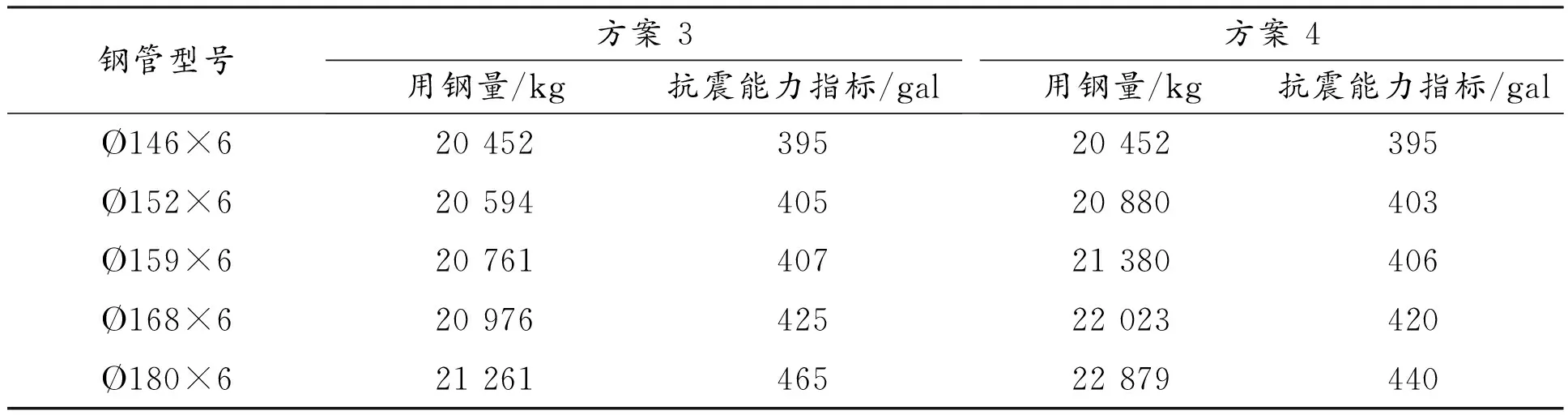
表2 结构抗震能力指标及用钢量列表
(5)对于方案6和方案7,用钢量增加比不超过5.56%时,前者对应的抗震能力不及后者,这是因为在此阶段,虽然前者下弦杆截面大于后者单根下弦杆,但构件截面高度对抗弯模量的影响更加明显,使得后者两条桁架拱抗弯模量的和要明显大于前者一条桁架拱抗弯模量,因此方案7的结构横向刚度比方案6明显要高,即使存在损伤集中效应,也被掩盖,使得同等用钢增量情况下,采用方案7的结构抗震能力明显超过方案6。不过,随着用钢量的进一步增加,作为常量的拱桁架截面高度对抗弯模量的影响随着下弦截面积的增加而逐渐相对降低,最终使得下弦截面面积大小成为决定构件截面抗弯模量的主导因素。因此,随用钢量增加,最终方案7效果超过方案6。
综合比较各方案,方案6、方案7在控制用钢量增量不超过7%的前提下,可保证抗震能力指标在770 gal以上,既兼顾材料经济性,又能较好保证0.8g峰值加速度内的结构安全性,满足实际地震动设防烈度要求。但是这两种方案施工费用较多,且存在较多的局部焊缝作业,实际工程中可能发生焊缝的预先破坏;方案2和方案3亦能保证结构安全性的同时,虽然材料用量稍多,但施工方法和费用较低,焊缝较少,亦可在实际施工中得到考虑。而方案5和方案6是费效比最差的方案,不适宜工程应用,方案1明显较方案2、方案3为差,此三方案在后文亦不予讨论。
4 参数分析
4.1 不同屋面荷载的影响
屋面质量对网壳的动力性能及抗震能力指标有着重要的影响。图7显示了本算例在屋面重力荷载为1.3 kN/m2和1.7 kN/m2条件下结构的抗震能力指标和用钢量增加比之间的关系曲线。
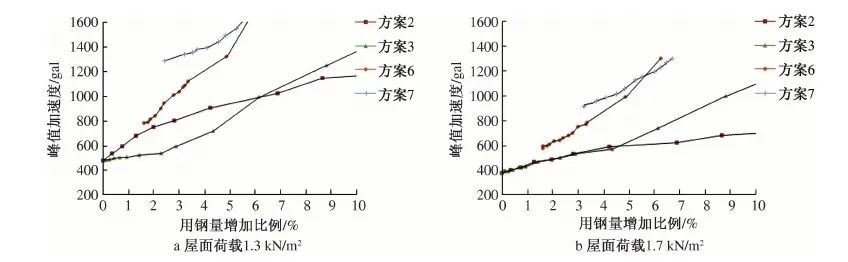
图7 不同屋面荷载作用下峰值加速度-用钢量增加比例关系曲线
与图4比较可以看出,随屋面荷载增加结构抗震能力急剧下降,证明屋面荷载是导致结构倒塌的重要因素。
(1)比较各方案对应曲线斜率变化,方案2下降最为明显,对屋面荷载变化最为敏感。
(2)由方案2和方案3对应曲线交点左侧两条曲线的竖向差距及该交点离开0点的水平距离,可以认为,由横杆截面分布不均匀导致的损伤集中现象导致的刚度下降随屋面荷载增加而变弱。
方案6在屋面荷载1.7 kN/m2时对应抗震能力指标在用钢增加比例不超过3.5%时,对应峰值加速度不超过800 gal,因此综合比较,在此屋面荷载作用下,只有方案7既能保证抗震能力标准,且用钢增量比例最小。在屋面荷载1.3 kN/m2时,方案6优势较为明显。可以预见,当屋面荷载极小时,施工简单的方案2将是最合适方案。
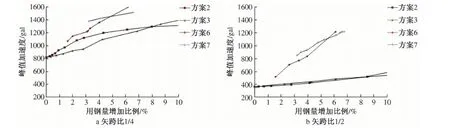
图8 不同矢跨比峰值加速度-用钢量增加比例关系曲线
4.2 矢跨比的影响
结构的矢跨比是影响结构横向刚度的重要因素,随着矢跨比增大,结构横向刚度总体降低,反之,横向刚度增加,反映在结构抗震能力曲线中,则如图8所示,低矢跨比结构抗震能力整体大于高矢跨比结构。通过比较,当矢跨比较高时,方案2和3对结构抗震能力提高相比方案6、7十分有限,费效比较差,同时方案6和方案7费效比有所上升。
综合用钢量增加比例、施工难度及抗震能力的要求,当矢跨比为1/4时,方案2显然为最优方案,而当矢跨比为1/2时,方案2和方案3不能保证地震峰值800gal内结构的安全,方案6在用钢量增加比例3.68%以上才能保证,而方案7在用钢量增加比例3.25%以上时即可确保结构安全,所以方案7显然是最优方案。
5 结论
针对提高纵边支承单层柱面网壳抗震能力的7个方案进行了计算分析,得到以下主要结论:
(1)通过提高横杆截面大小的方案比增强斜杆截面的方案有效,后者对结构抗震能力提高有限,不建议采用。而局部平面拱桁架方案比单纯增加横杆管径更为有效。
(2)当采用横杆管径增大方案时,既要注意同等用钢增量情况下,尺寸增大的集中化,又要注意损伤集中效应的影响。
(3)屋面重力荷载的增大均会降低结构的抗震能力。
(4)矢跨比的增大均会降低结构的抗震能力。
[1]中华人民共和国住房和城乡建设部.建筑工程抗震设防分类标准:GB 50223-2004[S].北京:中国建筑工业出版社,2004.
[2]中华人民共和国住房和城乡建设部.建筑抗震设计规范:GB 50011-2010[S].北京:中国建筑工业出版社,2014.
[3]曹资,薛素铎. 空间结构抗震理论与设计[M].北京:科学出版社,2005.
[4]徐赵东,李爱群,叶继红.大跨空间网壳结构减震控制的研究与发展[J].振动与冲击,2005,24(3):59-61.
[5]周海涛,张毅刚,吴金志.强震下单层纵边支承柱面网壳连续倒塌模式和机理[J].空间结构,2015,21(1):3-13.
[6]吕西林.超限高层建筑工程抗震设计指南[M].上海:同济大学出版社,2009.
Seismic patterns of single-layer cylindrical latticed shell and parameter analysis
ZHOU Hai-tao1,2, ZHANG Yi-gang2,3, WU Jin-zhi2
(1.HenanUniversityofUrbanConstruction,Pingdingshan467036,China;2.SpatialStructureResearchCenter,BeijingUniversityofTechnology,Beijing100124,China;3.KeyLabofUrbananddisasterEngineering,MOE,BeijingUniversityofTechnology,Beijing100124,China)
Based on the seismic capacity index, the peak ground acceleration at which the fist fracture-belt of shell come into being under severe earthquake. The mechanics performances of 7 seismic patterns is studied and it is proved that those pattern increasing the section of bars is much more effective than those increasing section of diagonals at the same steel volume. More analysis that proof load and ratio of rise-span is influential for seismic capacity and different pattern has different cost-effect ratio. To every situation, the best pattern is presented. The work is demonstrative and instructive value for project.
single-layer cylindrical latticed shell; seismic capacity index; seismic pattern; damage focus
2015-10-26
国家自然科学基金重大研究计划重点支持项目(90715034)
周海涛(1979-),男,宁夏中卫人,博士,讲师。
1674-7046(2015)06-0001-06
10.14140/j.cnki.hncjxb.2015.06.001
TU312+.3;TU323.3
A

