基于小波消噪-神经网络的钻孔数据预处理*

陈建均 胡乃联 李国清 马朝阳

(1.北京科技大学土木与环境工程学院；2.金属矿山高效开采与安全教育部重点实验室)

基于小波消噪-神经网络的钻孔数据预处理*

陈建均1,2胡乃联1,2李国清1,2马朝阳1,2

(1.北京科技大学土木与环境工程学院；2.金属矿山高效开采与安全教育部重点实验室)

针对地质品位信息存在系统噪声和测量噪声的问题，提出利用小波消噪的时频特性对钻孔数据进行预处理，然后运用神经网络的非线性和自适应性对消噪结果进行优化。将该方法应用于某露天钼矿的钻孔数据预处理，并通过克里金法进行品位插值。结果表明：采用钻孔数据预处理的插值效果优于未进行预处理的克里金法插值，验证了该方法的可行性和有效性。

小波消噪 神经网络 克里金法 SURFER

根据已知地质空间点的特性探索未知地质空间的特性是地质统计学应用研究的基本问题。常规方法难以对空间中所有点进行观测，但却可获取一定数量的空间样本，这些样本反映了已知空间的全部或部分特征，并可用空间插值方法来预测未知空间的特征[1]。常用的空间插值方法有克里格法，是对空间分布的数据求线性最优、无偏内插估计的一种方法[2]。信号的产生、处理及传输都不可避免地受到噪声的干扰，噪声的存在限制了人们提取原信号的有用信息。在地质勘探过程中，由于受众多因素的影响，空间信息含有系统噪声和测量噪声，一定程度上影响了地质系统的真实变化，从而影响预测精度[3]。通过小波消噪的时频特性、神经网络的非线性和自适应性对地质品位进行预处理，可提高数据的可靠性和数据分析结果的精度。本文以某钼矿为例，把小波消噪与神经网络结合起来，提出钻孔数据预处理方法，通过克里金插值进行对比分析。

1 钻孔数据预处理

1.1 小波消噪

小波分析是1974年由法国工程师J.Morlet首先提出，由于小波分析具备良好的时频特性，因而实际应用非常广泛。从数学的角度看，小波消噪问题的实质是寻找对原信号的最佳逼近；在信号学上，小波消噪是一个信号过滤的问题[4]。

1.1.1 基本原理

含噪声的一维信号数学模型表示为：

f(t)=s(t)+n(t) ,

(1)

式中,f(t)为含噪信号；s(t)为真实信号；n(t)为噪声信号。

最简单的情况下n(t)为高斯白噪声。小波变换就是要抑制n(t)以恢复s(t)，从而达到消除噪声的目的。从统计学的角度看，这个模型是一个随时间变化的回归模型，也可看作是在正交基上对函数s(t)的无参估计。

通过利用噪声和信号在小波变换下的不同特性，对小波分解系数进行处理，从而实现噪声和信号分离。通常情况下，噪声信号表现为高频信号，而有用信号则表现为较平稳的信号或者低频信号。

1.1.2 基本步骤

(1)选择一个小波，确定小波分解的层次M，找到合适的小波基，然后利用离散小波变换对含噪信号进行M层小波分解[5]，其中Harr小波函数定义如下：

(2)

(2)对第一层到第M层的每一层高频系数进行阈值量化处理，常用软阈值法和硬阀值法[6]。软阀值法将小于阀值的小波系数置零，并把大于阀值的小波系数向零做收缩，其表达式如下：

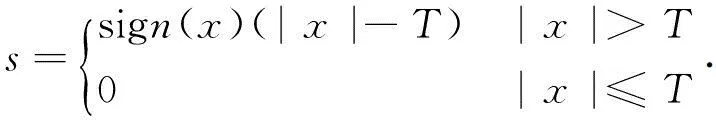
(3)

硬阀值法只保留大于阀值的小波系数，并将其他的小波系数置零，其表达式如下：

(4)

这两种方法各有差异，前者具有连续性，在数学上易于处理，后者更接近实际情况。

阀值处理的关键在于阀值的选择，若阀值太小，消噪后仍留有噪声；若阀值太大，重要的信号会被滤掉，引起偏差。

(3)根据小波分解第M层低频系数和经过量化处理后的第一层到第M层的高频系数进行信号的小波重构，表达式如下[7]：

(5)

式中，cj,n为尺度系数;dj，n为小波系数;h、g为一对正交镜像滤波器组;j为分解层数;n为离散采样点数。

1.2 神经网络

人工神经网络也简称为神经网络或连接模型，是模仿动物的神经网络行为特征进行分布式并进行信息处理的数学模型。这种网络是由人工神经元互联组成的,依靠系统的复杂程度，通过调整内部大量节点间相互连接，理论上可以逼近任意非线性映射。根据网络神经元连接方式的不同，可将人工神经网络分为相互连接型网络和分层网络，目前引用较广的是BP神经网络[8]。

(1)BP神经网络。该网络是一种多层前馈神经网络，一般含有三层，即输入层、隐含层和输出层，信息从输入层流向输出层。各层神经元仅与相邻层神经元之间相互全连接，同层内神经元之间无连接，各层神经元之间无反馈连接，构成具有层次结构的前馈型神经网络系统，无隐含层的前馈神经网络只能求解线性可分问题，具有隐含层的多层神经网络才能够求解非线性问题

(2)非线性。在客观世界中，很多系统的输入与输出间存在非常复杂的非线性关系，对于此类系统，往往难以通过传统的数理方法构建其数学模型。通过设计合理的神经网络，能够使系统输入-输出样本对进行自学习，从而以任意精度逼近复杂的非线性映射。神经网络的这一优良特性使其成为通用的多维非线性函数数学模型。

(3)自适应性。自适应性包含自学习和自组织两层含义。自学习是指当外界环境发生改变时，通过一段时间的训练或感知，神经网络能够自动调整网络结构参数，实现给定输入样本能够产生期望的输出样本。自组织是指神经系统在外部刺激下，根据一定规则调整神经元间的连接，逐渐构建神经网络。

1.3 钻孔数据预处理方法

①选择Harr小波作为小波基，对钻孔数据进行三层小波分解；②分别采用软阈值法和硬阀值法对分解后的每一层高频系数进行阈值量化处理，对比处理后的结果确定合适的阈值量化方法，并进行信号重构；③通过BP神经网络对小波消噪后的数据进行优化，使得最优拟合精度。

1.4 插值方法有效性评价

为了评价插值方法的质量，本文将数据样本总体分为两组，一组作为观测点(待估计点)，另一组作为已知点。通过已知点对观测点进行预测，采用均方误差(MSE)[9]作为验证指标。

(6)

均方误差越小，预测值就越接近真实值，插值效果也就越好。

2 应用实例

选取某露天矿的273个钻孔品位数据进行研究，选取253个样本点作为插值的初始值，其余20个样本点用来和插值结果进行对照。对照时，选用均方误差对这两种方法的结果进行评价。使用SURFER的格网分析功能，采样数据中品位作为Z值，存储在Data中，选择克里金插值。

选择Harr小波进行消噪处理，3层分解结果如图1所示。

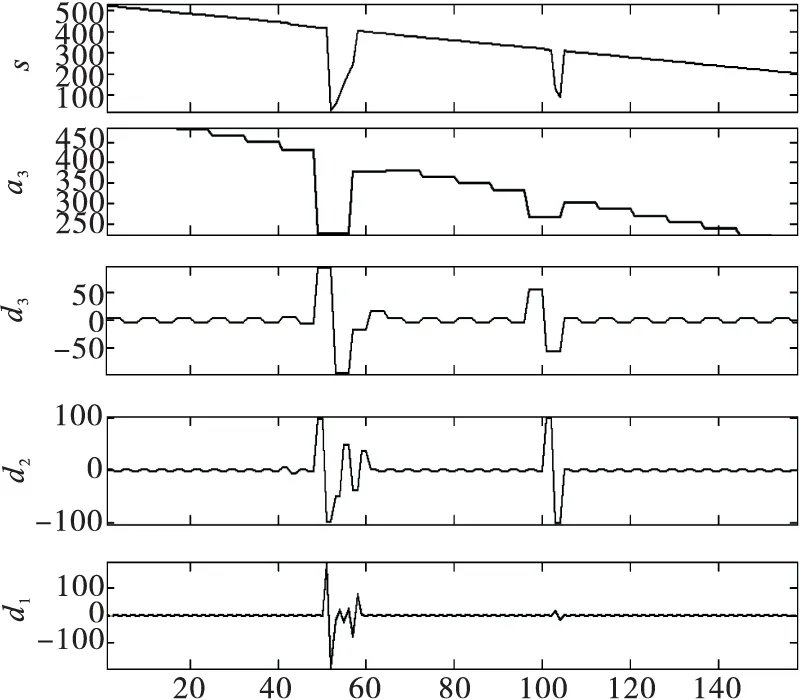
图1 Harr小波三层分解

小波消噪-神经网络钻孔数据预处理后，采用克里金插值、SURFER处理，结果如图2所示。图2中颜色越深，表示品位越高，反之，品位越低。

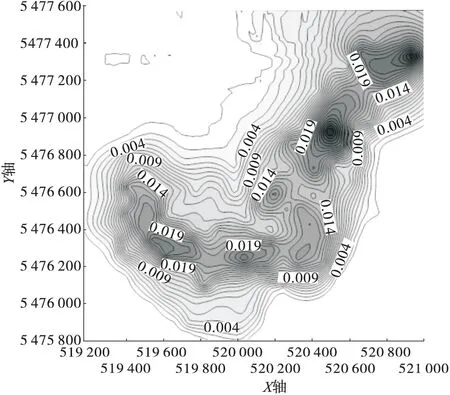
图2 钻孔数据预处理后的克里金插值

未进行钻孔数据预处理的直接采用克里金插值，运用SURFER处理，结果如图3所示。

对比图2和图3，可以明显看出二者在品位空间分布的变化趋势是一致的，但局部区域有一定的差异，相比处理前的克里金插值，采用钻孔数据预处理的克里金插值在预测范围上增加16.7%。

钻孔数据预处理前后的插值结果对比见表1。

由表1可以看出，经过钻孔数据预处理的克里金插值法的均方误差为2.368×10-8，优于未进行预处理的克里金插值，后者的均方误差为5.185×10-8。说明钻孔数据预处理能得到和观测值最为接近的插值结果，证明利用小波消噪-神经网络进行钻孔数据预处理是有效的。

图3 未进行钻孔数据预处理的克里金插值

表1 已知钻孔的两种插值结果对比

3 结 论

(1)地质钻孔数据由于受到噪声干扰，直接运用克里金插值会影响准确性。小波变换是一种信号时频分析方法，能够有效地对信号进行消噪；神经网络具有非线性和自适应性，能够对消噪后的数据进行二次优化。

(2)以某钼矿的钻孔数据为例，通过对比，发现基于小波消噪和神经网络的钻孔数据预处理能够有效地提高克里金插值的精度。因此，在进行克里金插值前，有必要进行钻孔数据预处理。

[1] 刘 钊，谢颖立．用遗传算法改进模糊隶属度克里金插值的研究[J].测绘科学，2012，37(4):191-193．

[2] 伍 伟，任卓隽，薛欣玲，等．曼家寨锌矿体储量基于克里金法的计算[J].矿业工程，2011，9(5):13-15．

[3] 徐长发，李国宽．实用小波方法[M].武汉:华中科技大学出版社，2009．

[4] 杜浩藩，丛 爽．基于MATLAB小波去噪方法的研究[J].计算机仿真，2003(7):119-122．

[5] 王秀杰，练继建，费守明，等.基于小波消噪的混沌多元回归日径流预测模型[J].系统仿真学报,2007，19(15):3605-3608.

[6] 秦永宽，黄声享，赵 卿.基于小波消噪和LS-SVM的混沌时间序列预测模型及其应用[J].大地测量与地球动力学,2008，28(6):96-100.

[7] 文 莉，刘正士，葛运建.小波去噪的几种方法[J].合肥工业大学学报:自然科学版,2002，25(2):167-172.

[8] 孟召平，田永东，雷 旸.煤层含气量预测的BP神经网络模型与应用[J].中国矿业大学学报,2008,37(4)：456-461.

[9] 武俊红，汪云甲.基于Surfer的煤矿等值线空间插值方法有效性评价[J].中国矿业,2007,16(1):108-110.

Drilling Data Pre-processing Based on Wavelet De-noising and Neural Network

Chen Jianjun1,2Hu Nailian1,2Li Guoqing1,2Ma Zhaoyang1,2

(1.Civil and Environmental Engineering School,University of Science and Technology Beijing;2.State Key Laboratory of High-Efficient Mining and Safety of Metal Mines(Ministry of Education))

Aiming at the problem of the system noise and measurement noise of geological grade information,a data pre-processing is proposed. The method adopts the time-frequency characteristics of wavelet de-noising to drilling data pre-processing, and then apply the nonlinear and adaptability of neural network to optimize it. The method is applied to the drilling data pre-processing in an open molybdenum ore, and grade estimation by Kriging interpolation. The results shows that,the effect of interpolation of the method is better than that without data pre-processing kriging interpolation method. It demonstrates that the method is feasible and effective.

Wavelet de-noising, Neural network, Kriging method, SURFER

*“十二五”863计划项目(编号：2012AA062200)；国家自然科学基金项目(编号:51104010)。

2014-10-10)

陈建均(1989—)，男，硕士研究生，100083 北京市海淀区学院路30号。