格上适应性安全可撤销的基于身份签名方案

向新银

（西安财经学院信息学院，西安 710100）

格上适应性安全可撤销的基于身份签名方案

向新银

（西安财经学院信息学院，西安 710100）

传统基于身份的签名方案的安全性依赖于密钥的安全，一旦密钥泄露，则需重新发布先前所有的签名。为撤销签名方案中私钥泄露或恶意的用户，提出一个可撤销的基于身份签名方案，并给出解决密钥泄漏的有效方法，在小整数解困难问题下，能抵抗适应性选择消息攻击的强不可伪造性。安全性分析结果表明，该方案不仅满足原有可撤销的基于身份的签名方案的可证明安全性，而且还能抵抗量子攻击。

适应性安全；基于身份签名；格；小整数解；后量子密码

1 概述

为简化公钥的管理，文献［1］提出了基于身份的密码学原语，其思想是用户的公钥可由用户的身份信息（邮件地址、身份证号码等）生成，私钥由可信任第三方密钥生成器生成。2001年，Boneh和Franklin［2］构造了第一个实用的基于身份加密体制，并成功地将双线性对运用到公钥密码体制中。2002年，Paterson［3］利用双线性对，构造了一个新的基于身份的签名方案，但该方案效率较低。文献［4］基于CDH的困难假设提出改进方案，该方案的计算效率和签名大小都有较大的提高。2009年，Tseng等人［5］在随机预言模型下提出了一个可证明安全的基于身份的签名方案，但是他们的方案并不支持强不可伪造性。

随着公钥密码体制的发展，特别在一些安全性较差的环境中，密钥容易泄露。如何遏制密钥泄露的发生，可以通过撤销密钥来解决。2008年，Boldyreva等人［6］应用二叉树结构构造一个可撤销的基于身份的加密方案，该方案尽管减少了密钥更新的大小，但是需要通过安全信道周期地传输新的用户私钥，导致加密和解密过程的计算开销过大。文献［7］提出了一个实用的可撤销方案。文献［8］在随机预言模型下提出了一个可撤销的基于身份的签名方案。然而，以上方案大多是在随机预言模型下证明其安全性。虽然在随机预言模型下构造的密

码方案效率较高，但是在随机预言模型中，一些学者也指出某些方案在哈希函数实例化后并不安全。因此，考虑无随机预言的标准模型下构造可撤销的基于身份的签名方案具有十分重要的意义。

从文献［9］构造了一类随机格后，格公钥的研究受到了广泛的关注。文献［10］构造了格上可撤销的基于身份的加密方案，但是该方案仅支持选择性安全。随后，文献［11］基于文献［10］方案提出一个格上可撤销的基于身份适应性安全的加密方案。目前还没有格上可撤销的基于身份的签名方案，为此，本文利用文献［12］的技术，构造了一个格上适应性安全的可撤销的基于身份的签名方案。

2 预备知识

定义相关参数：令q表示一个素数，PPT表示概率多项式时间。

其中，ν1，ν2，…，νm是一组线性无关的向量。

定义2（离散高斯分布） 令一个任意的正参数ρ＞0，c∈Rm，实数σ＜0，定义格Λ上的离散高斯分布为其

3 方案形式化定义和安全模型

3.1 形式化定义

一个可撤销基于身份的签名方案由以下5个算法组成［3］：

（1）参数建立：输入一个安全参数 λ，输出系统公开参数PP。

（2）密钥提取：输入一个用户的身份标识 id，输出用户的私钥skid。

（3）密钥更新：输入一个用户的身份标识 id和时间周期t，输出用户的私钥skt。

（4）签名：输入公开参数PP，时间周期t的公钥Pkt和私钥skt，输出签名σ。

（5）验证：输入用户的身份标识 id，时间周期 t和消息 m的签名 σ，如果签名 σ是否有效，输出1；否则，输出0。

3.2 安全模型

定义4（强不可伪造性） 一个可撤销的基于身份的签名方案满足选择消息攻击下强不可伪造性，即如果没有敌手A在sUF-CMA游戏中以不可忽略的优势取胜。这里的sUF-CMA游戏是在一个算法B和敌手A之间进行。

（1）参数建立：输入安全参数 λ，B运行此算法生成系统参数和密钥，并公开系统参数。

（2）询问：A适应性执行如下询问：

1）密钥提取询问：输入用户的身份标识id，运行密钥提取算法生成私钥并返回给A。

2）密钥更新询问：输入用户的身份标识id和时间周期t，运行密钥更新算法生成更新私钥并返回给A。

3）签名询问：输入系统参数，用户的身份标识id和时间周期 t，签名算法生成一个签名 σ，并发送给A。

（3）伪造：A输出用户身份标识 id*，消息 m*，时间周期t*和签名σ*。如果（id*，m*，t*）在询问阶段没有被询问过且验证有效，则A赢得此游戏。

4 可撤销的基于身份的签名方案

（1）参数建立：输入一个安全参数 λ，此算法执行如下：

1）运行陷门生成算法TrapGen（q，n，m）生成一个矩阵和上的一个短基 TA0∈，使得

2）选取2 l+2个n×m的矩阵A1，A2，…，Al，B，

4）输出公开参数 PP=（A0，A1，…，Al，B，C，D1，…，Dl，u），保存主密钥msk=TA0。

（2）密钥提取：输入公开参数PP，主密钥 msk，一个身份标识 id=（b1，b2，…，bl）∈｛-1，1｝l，此算法执行如下：

2）计算Tid←EχtBasis（A0，Aid，TA0）。

3）输出公钥Pkid=Aid，私钥skid=Tid。

（3）密钥更新：输入公开参数PP，用户私钥skid，一个用户的身份标识id=（b1，b2，…，bl）∈｛-1，1｝l和任意的时间周期t=（t1，t2，…，tl）∈｛-1，1｝l，此算法执行如下：

2）计算Tt←EχtBasis（A0，Fid，t，Tid）。

3）输出公钥Pkt=Fid，t私钥skt=Tt。

（4）签名：输入公开参数PP，一个任意的时间周期t=（t1，t1，…，tl）∈｛-1，1｝l，用户的更新密钥对（Pkt，skt）和消息m∈｛0，1｝*，此算法执行如下：

1）计算e←SampleLeft（A0，Fid，t，Tt，u，δ）。

2）输出签名σ=e。

（5）验证：输入消息 m和签名 σ，验证者进行如下算法：

2）Fid，te=u。

如果以上条件同时成立，则签名有效，输出1；否则，输出0。

5 方案的安全性分析

定义4 假设H：=｛H：X→Y｝是一个从X映射到Y的哈希函数，对于任意的Q+1个集合χ—=（χ0，χ1，…，χQ）∈XQ+1，定义 χ—非退化的概率为：

其中，概率为H在H：中的随机选择。

H抗退化碰撞的定义如下：给定任意的χ—=（χ0，且 χ0≠（χ1，χ2，…，χQ），存在

其中和 h=（h1，

定理 在SIS困难问题下，新方案满足标准模型下的适应性选择消息攻击的强不可伪造性。

证明：假设存在一个多项式时间的敌手A，构造一个不可区分的算法B解SIS问题，即输入任意一个矩阵A′，找到一个非零向量e≠0，使得A′e=0。具体游戏在A和B之间共同进行。

参数建立：B为应对SIS挑战，执行如下算法：

（1）任意抽取 2个矩阵和其相应的陷门（B，TB）←TrapGen（q，n，m），（E，TE）←TrapGen（q，n，m）。

（5）选取一个随机向量u∈Znq。

（6）输出公开参数 PP=（A0，｛Aid，i｝i=1，2，…，l，｛At，i｝i=1，2，…，l，B，E，u），保存主密钥msk=（TB，TE），并将PP发送给敌手A。

询问：B在消息m上应对敌手A多项式次用户密钥生成，密钥更新和密钥撤销询问的应答。首先输入一个身份标识 id=（b1，b2，…，bl）∈｛-1，1｝l，过程如下：

（1）密钥提取询问：为了响应A对id=（b1，b2，…，bl）∈｛-1，1｝l密钥提取询问，B执行以下操作：

如果hid≠0，这时A0‖A0Rid+hidB。B执行如下算法：Tid←EχtBasis（A0，Kid，TA0），并返回skid=Tid给A。

（2）密钥更新询问：为了响应A对t=（t1，t2，…，的密钥更新询问，B执行如下算法：

3）对于t=（t1，t2，…，tl）∈｛-1，1｝l，计算Tt←EχtBasis（A0，Fid，t，Tid）。

并返回私钥skt=Tt给A。

（3）签名询问：为了响应 A对消息 m∈｛0，1｝*上的签名询问，B执行如下算法：

1）如果hid≠0，即有：e←Sam pleRigh t（Fid，t，Tt，u），输出签名e。

2）如果hid=0或者ht=0，这里TB或者TE的作用消失，B重新构造一个签名e，并发送给敌手A。

伪造：A在时间周期t*内对身份标识id*和消息生成了一个伪造签名 e*。假设或者ht*=0时产生的概率为1/2λ，对于任意的 hid*≠0和ht*≠0，即有：Fid*，t*e*=u，Fid*，t*e=u，则Fid*，t*（e*-e）=u-u。

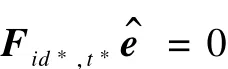
仅考虑如下情况，如果hid*=0和ht*=0，则：

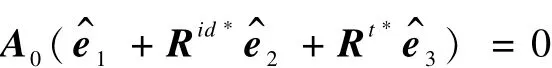
6 结束语

本文基于文献［12］的技术，提出一个格上适应性安全的可撤销的基于身份的签名方案，并证明了该方案在标准模型下，基于SIS困难问题满足适应性选择消息攻击的强不可伪造性（sUF-CMA）。该方案提供了可撤销性和更好的安全性，可以推广到选择性安全的可撤销的基于身份的签名方案。

［1］ Shamir A.Identity-based Cryptosystems and Signature Schemes［C］//Proceedings of Crypto’84，Santa Barbara，USA：IEEE Press，1984：47-53.

［2］ Boneh D，Franklin M.Identity-based Encryption from the Weil Pairing［C］//Proceedins of Crypto’01.Santa Barbara，USA：IEEE Press，2001：213-229.

［3］ Paterson K，Schuldt J.Efficient Identity-based Signatures Secure in the Standard Model［C］//Proceedings of the 11 th Australasian Conference on Information Security and Privacy.Melbourne，Australia：［s.n.］，2002：207-222.

［4］ Cha JC，Cheon J H.An Identity-based Signature from Gap Diffie-Hellman Groups［C］//Proceedings of the 6 th International Workshop on Practice and Theory in Public Key Cryptography.Miami，USA：IEEE Press，2003：18-30.

［5］ Tseng Y M，Wu TY，Wu JD.A Pairing-based User Authentication Scheme for Wireless Clients with Smart Cards［J］.Informatica，2008，19（2）：285-302.

［6］ Boldyreva A，Goyal V，Kumar V.Identity-based Encryption with Efficient Revocation［C］//Proceedings of the 15th ACM Conference on Computer and Communications Security.New York，USA：ACM Press，2008：417-426.

［7］ Tsai T T，Tseng Y M，W u T Y.Provably Secure Revocable ID-based Signature in the Standard Model［J］.Security and Communication Networks，2013，10（6）：1250-1260.

［8］ Sun Yinxia，Zhang Futai，Shen Linmin，et al.Revocable Identity-based Signature Without Pairing［C］//Proceedings of the 5th International Conference on Intelligent Networking and Collaborative System s.X i’an，China：［s.n.］，2013：363-365.

［9］ Ajtai M.Generating Hard Instances of Lattice Problems［C］//Proceedings of the 28th Annual ACM Symposium on Theory of Computing.New York，USA：ACM Press，1996：99-108.

［10］ Chen Jie，Lim L M，Ling Sen，et al.Revocable Identitybased Encryption from Lattices［C］//Proceedings of the 17th Australasian Conference on Information Security and Privacy.Wollongong，Australia：［s.n.］，2012：390-403.

［11］ 张彦华，胡予濮，江明明，等.格上可撤销的基于身份的适应性安全的加密方案［J］.电子与信息学报，2015，37（2）：423-428.

［12］ Agrawal S，Boneh D，Boyen X.Efficient Lattice（H）IBE in the Standard Model［C］//Proceedings of Eurocrypt’10.Riviera，French：［s.n.］，2010：553-572.

编辑 索书志

Adaptive Secure Revocable Identity-based Signature Scheme over Lattices

XIANG Xinyin
（School of Information，Xi’an University of Finance and Economics，Xi’an 710100，China）

The security of traditional identity-based signatures wholly depends on the security of secret keys.Exposure of secret keys requires reissuing all previously assigned signatures.Based on this，to revoke private key leaks or malicious users in the signature scheme，an adaptive secure revocable identity-based signature over lattices is proposed，which provides an efficient revocation mechanism to revoke misbehaving or compromised users from the system s.The scheme is proved to be strongly Unforgeable against adaptive Chosen-message Attacks（sUF-CMA）under Small Integer Solution（SIS）assumption.Security analysis results show that the proposed scheme not only can meet the security of revocable identity-based signature，but also can resist the quantum attack.

adaptive secure；identity-based signature；lattice；Small Integer Solution（SIS）；post-quantum cipher

向新银.格上适应性安全可撤销的基于身份签名方案［J］.计算机工程，2015，41（10）：126-129.

英文引用格式：Xiang Xinyin.Adaptive Secure Revocable Identity-based Signature over Lattices［J］.Computer Engineering，2015，41（10）：126-129.

1000-3428（2015）10-0126-04

A

TP309

10.3969/j.issn.1000-3428.2015.10.024

国家统计科学研究计划基金资助项目（2013LY052）；陕西省自然科学基金资助项目（2012JM 8018，2014JM 2-6099）；陕西省教育厅科学计划基金资助项目（2010JK553，2013JK1193）；西安财经学院基金资助项目（13XCK 01）。

向新银（1979-），男，讲师、博士，主研方向：格公钥。

2015-04-17

2015-05-19E-mail：xiangxinyin@hotmail.com