双向节理岩石边坡稳定性的随机数值分析★

许 娇 郭 鸿* 高 斌

(陕西理工学院土木工程与建筑学院，陕西 汉中 723000)

〗dt

K=f(H,α,φ…)

；。

。

。

。

。

；

；

。



双向节理岩石边坡稳定性的随机数值分析★

许 娇 郭 鸿* 高 斌

(陕西理工学院土木工程与建筑学院，陕西 汉中 723000)

利用蒙特卡罗随机数值模拟方法，对双向节理岩石边坡的稳定性进行了计算分析，结果表明，坡角越小，孔隙水压力越小，岩石边坡安全系数分布值越大，且孔隙水压力对安全系数的影响作用更大。因此，和人工削坡相比，排水措施是提高岩质边坡稳定性更为有效和经济的方法。

岩质边坡，失稳破坏，蒙特卡罗方法

近年来，国内外对于高速公路和铁路落石与崩塌的报道屡见不鲜，这种事故主要是由于岩质边坡的失稳破坏诱发的，此种现象广泛存在于高速公路，露天开采以及水利水电工程中，岩质边坡失稳破坏已成为岩土工程界广泛关注的问题之一。大型崩塌不仅可以成段毁坏道路和各类建筑物，而且堵塞河道，淹没良田和建筑物，甚至会造成严重水灾。灾难一旦发生，会给国家和人民造成巨大经济损失，直接影响人民的生活[1-3]。岩质边坡的主要破坏形式以滑动破坏和倾倒破坏为主，一般分为岩石结构面组合交线方向的滑动或倾倒及顺层里的滑动或倾倒两种类型。对于边坡工程安全性的评价指标，传统的评价方法是以稳定性系数作为研究参数，其结果的准确性依赖于计算模型的吻合程度和计算参数的准确性。在工程实践中，对于有些滑坡由于要考虑不确定因素的影响，所以安全系数的值并不能唯一确定。

蒙特卡罗方法的实质是通过大量的随机试验，利用概率论解决问题的一种数值方法。它是一种模拟随机的运动但能得出确定的结果的研究方法，不仅能给出滑坡的平均安全系数，也能给出滑坡可能存在的风险，能客观反映滑坡的安全程度，在求解滑坡稳定可靠性指标和破坏概率方面无疑是一种行之有效的方法，已广泛应用于岩质工程问题分析。

1 蒙特卡罗方法的基本原理

蒙特卡罗方法就是边产生随机数边进行随机模拟的方法。它的实质是通过大量随机实验确定出一组随机数，利用(0,1)区间内的均匀随机数产生一个随机变量，从而得出确定的结果。

所以，如何确定出已知分布的随机数是利用蒙特卡罗模拟法分析滑坡稳定性的核心问题。由正态分布的概率密度可知，其累积概率为：

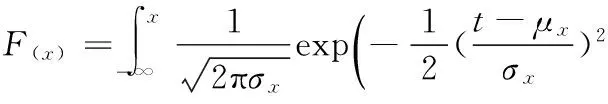
(1)

另外，蒙特卡罗模拟是由具有已知分布的总体中抽取简单子样，这就表明抽取样本数目的大小影响着概率计算的精度。一般来说，样本数目N越大，边坡失稳率Pf的绝对误差ε越小。由于边坡失稳概率的数值特别小，所以样本数目必须足够大，对于滑坡工程，一般取N=5 000～10 000来满足精度要求。

2 双向节理岩石边坡模型

目前，对岩质边坡的倾倒分析都是建立在如图1所示的地质模型基础上的，即边坡分布一组与边坡走向一致的平行等间距的主控裂隙组—层理，页理等。受横向裂隙组切割，形成一个以台阶形斜面为潜在破坏面的离散岩块集合体，它的稳定性分析主要是以单个岩块为基础。ψa为滑动面倾角，ψb为倾倒面的倾角，Sa为相邻滑动面间的距离，Sb为相邻倾倒面的距离，ψs为自然方向的倾角，ψts为坡顶面的倾角。

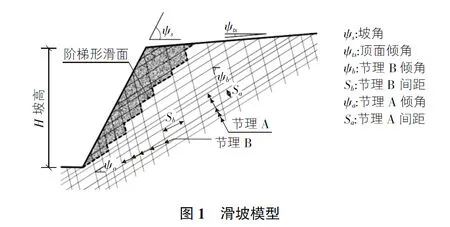
3 双向节理岩石滑坡安全系数破坏概率的蒙特卡罗法模拟

蒙特卡罗方法的实质是用随机数进行计算模拟，它需要某种分布的随机变量。它的基本思想是：根据已知变量的概率分布类型，利用蒙特卡罗方法产生和状态变量概率已知的若干随机数。在此基础上，将产生的随机数代入需要分析的功能函数中。产生N组随机数，则可以得到N个功能函数K值。在滑坡分析这个具体问题中，N组初始值则可以产生N个K值(K为安全系数)，若其中有M个值小于1，则滑坡的概率为M/N。

边坡安全系数的大小与边坡的几何参数如边坡高度H、边坡倾角α以及其力学参数如内摩擦角φ有着密不可分直接的关系，它们之间的关系如下列关系式：

K=f(H,α,φ…)

(2)

边坡安全系数K的概率密度函数为：

(3)

K的密度函数f(K)可以是任意分布函数，其破坏概率可以看作均匀分布(0,1)对f(x)取样的积分求得。由于在自然现象中，大量随机变量都服从或近似服从正态分布，其基本理论是来源于概率论中的中心极限定理。因此上述随机变量的参数均按正态分布取值，随后根据蒙特卡罗模拟得出安全系数K的分布规律。

4 岩质边坡破坏的理论分析

4.1 倾倒滑移破坏的计算模式

在研究多层单条柱受力平衡时，要考虑它的多层分块性。在二维坐标系中，对一个单条柱的第i块，可以列出下列平衡方程：

设α为基底的倾角，φ为基底的内摩擦角，据Aydan O等人的推论可得出以下四种情况：

1)不产生滑动与倾角的稳定条件：

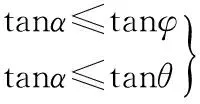
2)仅产生滑动的条件：

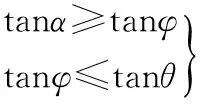
3)仅产生倾倒的条件：

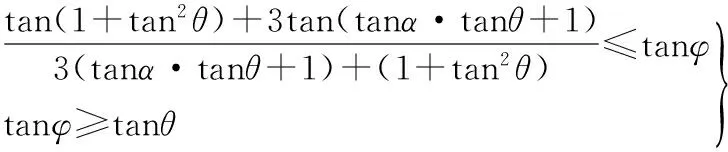
4)同时滑动与倾倒的条件：

4.2 平面滑动分析

大多数岩坡滑动之前在坡顶上或在坡面上会出现裂缝，如图2所示。裂缝中不可避免会存在水，从而存在侧向水压力，使岩坡的稳定性降低。

在分析时，假设滑动面及张裂缝的走向与坡面平行；张裂缝垂直，Zw为充水深度；水沿张裂缝底进入滑动面渗漏，张裂缝底与坡趾间的长度内水压力呈线性分布；滑动块体重量W，滑动面上水压力U和张裂缝中水压力V均通过滑体重心，也就是说破坏仅是由于块体滑动引起的。忽略岩块转动的力矩造成的误差。

根据图2，潜在滑面上的安全系数Ks,可按极限平衡条件求得：

(4)

其中，L为滑动面长度(每单位宽度内的面积),m,由下式表示：

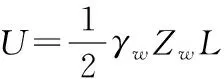
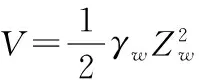
5 随机数值稳定分析

5.1 边坡倾角对安全系数分布的影响

根据式(1)～式(4)可以做出在不同坡角的情况下，安全系数Ks的概率分布如图3所示。从图3四组数据显示可以看出：安全系数Ks与坡角有显著的关系，在保持孔隙水为50%的情况下，随着坡角的增大，安全系数Ks<1的频数越高，边坡越容易失稳。即边坡坡角越大，安全系数Ks<1的概率越大，边坡稳定性越差。

5.2 孔隙水压力对安全系数分布的影响

根据式(1)～式(4)可以做出在保持边坡倾角为60°的情况下，安全系数Ks的概率分布如图4所示。

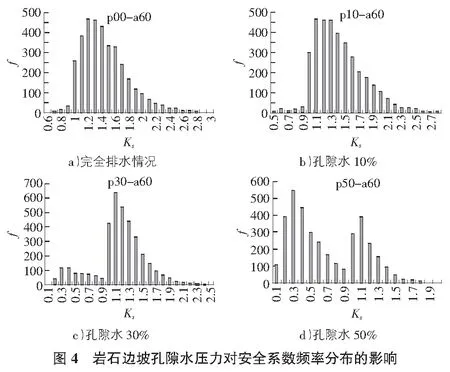
根据图4四组数据显示：在边坡坡角保持为60°不变的情况下，边坡完全排水时，安全系数Ks<1的频数几乎为0，随着孔隙水压力逐渐的增大，安全系数Ks<1的频数随之增大，边坡的稳定性逐渐减弱。即在其他条件保持不变的情况下，孔隙水压力对边坡的稳定性有着显著地影响，孔隙水压力越大，边坡稳定性越差。

6 结语

1)通过运用蒙特卡罗随机模拟方法对边坡倾角与边坡安全稳定系数Ks之间关系的研究，根据理论数据分析可以知道边坡倾角是影响边坡稳定性的重要因素之一，边坡倾角越大，边坡安全系数Ks<1的频数越大，边坡稳定性越差。

2)在保持其他因素不变的情况下，孔隙水压力对边坡稳定性有着显著的影响。孔隙水压力越大，边坡越容易失稳。

3)对于边坡施工中，为了提高边坡的稳定性，应尽可能的把边坡倾角或孔隙水压力控制在一定的安全范围内。

[1]刘才华,陈从新.地震作用下岩质边坡块体倾倒破坏分析.岩石力学与工程学报,2010(S1):3193-3198.

[2]万 洪,胡春林.地震荷载作用下岩质边坡稳定性分析.建材世界,2009(3):106-109.

[3]田剑锋,马 超,赵 甫.公路岩质边坡稳定性评价方法研究.公路,2008(7):65-68.

[4]王建锋,Wilson HTang,崔政权.块状岩体边坡倾倒破坏稳定性分析.中国地质灾害与防治学报,2001(4):3-10.

[5]张光鹏.基于蒙特卡罗法的黄土滑坡稳定性研究.兰州：兰州大学,2013.

[6]杨保军,何 杰,吉 刚,等.岩质边坡滑动—倾倒组合破坏模式稳定性分析.岩土力学,2014(8):2335-2341，2352.

[7]熊传治.岩石边坡工程.长沙：中南大学出版社，2010.

Stochastic numerical analysis of double jointed rock slope stability★

Xu Jiao Guo Hong* Gao Bin

(ShaanxiUniversityofTechnology,CollegeofCivilEngineeringandArtitecture,Hanzhong723000,China)

The paper applies Monte Carlo stochastic numerical simulation method, and calculates and analyzes double jointed rock slope stability. Results show that: the bigger the slope angle is, the smaller the pore water pressure, the bigger the rock slope safety coefficient distribution value is, and the greater the pore water pressure upon safety coefficient. Thus, comparing to artificial slope cutting, drainage measures is more effective and economic method for improving rock slope stability.

rock slope, instability failure, Monte Carlo method

1009-6825(2015)18-0052-03

2015-04-15★：陕西省教育厅项目支持和陕西理工学院大学生创新训练计划支持

许 娇(1993- )，女，在读本科生； 高 斌(1993- )，男，在读本科生

郭 鸿(1984- )，男，博士，讲师

TU413.62

A