大定源瞬变电磁一维自适应正则化反演

徐玉聪，赵 宁，秦 策，王 锐，张召彬

(1. 成都理工大学地球物理学院，四川成都 610059；2. 河南理工大学计算机学院，河南焦作 454000)



大定源瞬变电磁一维自适应正则化反演

徐玉聪1，赵 宁2，秦 策1，王 锐1，张召彬1

(1. 成都理工大学地球物理学院，四川成都 610059；2. 河南理工大学计算机学院，河南焦作 454000)

自适应正则化反演对初始模型要求较低，直接对瞬变电磁响应数据进行反演。正则化因子通过计算每次迭代的数据目标函数和模型目标函数自适应的得到,从而快速获得地下的地电结构。本文采用自适应正则化反演算法对大定源回线瞬变电磁一维层状模型进行反演，使用均匀半空间作为初始模型，首次采用模型对深度的二阶导数极小的模型约束，通过典型理论模型的反演计算，证明了TEM自适应正则化一维反演算法拟合效果好、精度高，由于不用反复搜索正则化因子，并且收敛速度快，体现了良好的稳定性和可靠性。

瞬变电磁 大定源 自适应正则化反演 最光滑模型约束

Xu Yu-cong, Zhao Ning, Qin Ce1, Wang Rui, Zhang Zhao-bin. One-dimensional adaptive regularization inversion of transient electromagnetic sounding with a large fixed source[J]. Geology and Exploration, 2015, 51(2)：0360-0365.

1 引言

瞬变电磁法是通过对观测到的二次场响应信息进行提取分析，从而获得地下介质的地电结构。大定源回线装置发射线圈一般采用边长数百米的矩形回线,由于布设一次发射回线能够在多个点同时接收,因此该方法工作效率相对其他装置要高的多，所以广泛应用于许多工程领域(朴化荣，1990；李貅等，2002)。因此需要寻找一种稳定、可靠的反演解释方法。

一维瞬变电磁反演解释常用有两种思路,一种是最优化反演,一种是烟圈反演。烟圈理论最早是由M.N.Nabighian等提出的，这是一种近似反演方法,反演速度非常快,而且不依赖初始模型,不过由于反演结果不能提供与层厚相关的信息,而且精度达不到要求,因此,烟圈反演往往只用来做定性分析。目前常用最优化反演方法是最小二乘，由于最小二乘只是尽量拟合观测数据，对反演模型约束不够，所以难以获得好的反演结果；翁爱华(翁爱华等，2007)采用OCCAM反演法直接对感应电动势进行反演，OCCAM方法可以获得很好的反演效果，由于OCCAM反演(Constable S C,1987)方法每次迭代要多次正演计算，所以耗时较长。

本文结合大定源回线瞬变电磁的具体特点，采用陈小斌(陈小斌等，2005)自适应正则化反演法，实现了约束模型下的正则化反演，其中正则化因子通过自适应的方式给出，避免了OCCAM反演中为搜索正则因子进行的大量正演计算过程，因此通过极少的迭代次数和计算时间即可获得较好的的反演结果。

2 自适应正则化反演算法原理

正则化反演是基于尽可能拟合观测数据，同时获得最理想的约束模型的一种算法，其基本思路是把地下介质分成多层层状结构，把每层厚度加入模型约束函数，即粗糙度矩阵，通过计算得到每层电阻率，从而构建地下地电结构。其总目标函数可归结为：

(1)

式中φ(m)为总目标函数；λ为正则化因子；φm(m)为模型约束目标函数；φd(m)为观测数据目标函数；m为模型向量。

其中(1)式中观测数据目标函数φd(m)可表示为

(2)

式(2)中Δd是观测数据与理论响应差向量；Wd为数据加权矩阵；F为正演算子；J为经过泰勒级数展开后正演响应对电阻率的偏导数矩阵，即雅克比矩阵。

模型约束目标函数φm(m)由(3)式给出

(3)

φm(m)中Rm粗糙度矩阵，m为模型向量；目前φm(m)构建方式有三种，即最小约束模型、最平缓约束模型、最光滑约束模型；模型约束目标函数的构建可完全转化为粗糙度核矩阵Rm的计算，本文采用最光滑模型约束(模型对深度的二阶导数)。

其构建方式如下：Rm=Rn×n，h0、h1…hn为模型层厚距离地面垂直深度。

(4)

正则化因子采用陈小斌提出的CMD方案：

(5)

式(5)中k表示第k次迭代反演，通过自适应的调节正则化因子λ，可以平衡观测数据目标函数和模型约束目标函数的权重，从而获得最佳拟合结果。

将(1)式对模型向量求偏导数，并做线性化处理，根据极小化原则，可得到反演方程：

(6)

式(6)中Δm为待求的模型修正向量，Jk为当前模型的雅克比矩阵；解此线性方程，获得模型修正量，进而得到下一次迭代反演的初始模型mk+1，其中mk+1=mk+Δm。

反演的终止条件定义为：

当反演拟合差小于给定RMSinit，或者反演迭代达到最大迭代次数，即终止反演，获得局部最优的反演模型。

3 反演算例

为检验上述反演算法的可靠性，利用层状介质模型的理论正演数据加4%的随机噪声作为反演数据，对大定源发射线框内不同测点数据进行反演。大回线瞬变电磁装置参数设置如下：发射线圈为正方形线圈，线圈匝数设置为1，边长200 m, 发射电流10 A,接收线圈接收面积为1 m2，匝数为1。装置布置如图1，a1、a2处为测点，三层和四层模型的反演初始模型，均采用100 Ω·m的均匀半空间。

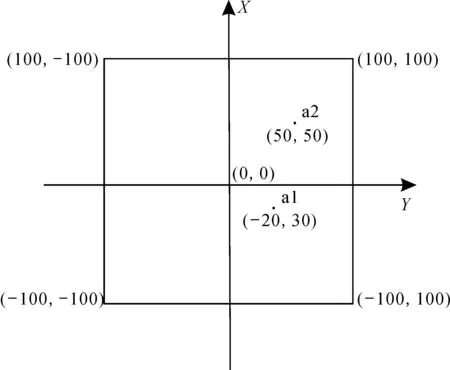
图1 大定源装置布置图Fig.1 Measurement map of large fixed source transient electromagnetic device

3.1 三层模型反演试算

三层模型中最典型的是H型和K型地电模型，图2所示是H型模型(各层电阻率分别为300 Ω·m、50 Ω·m、300 Ω·m，层厚为100 m、100 m)测点a1的反演结果，反演第3次得到的修正模型已经基本反映出了200 m～300 m的相对高阻层，随着反演迭代次数的增加逐渐逼近真实模型的电阻率和深度；从图2所示理论数据和反演迭代响应数据曲线对比，可以看出反演迭代响应数据快速拟合理论数据，在最佳修正模型结果下的反演迭代数据和原始数据相对拟合差下降到1.5e-3,几乎完全拟合了原始理论数据。反演过程中正则化因子和相对拟合差快速下降，可以看出自适应正则化反演算法能够快速稳定的收敛。

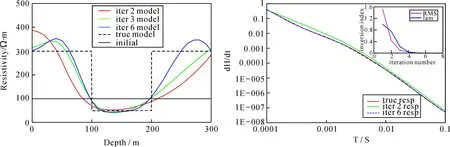
图2 H型模型测点a1反演结果以及拟合差、正则化因子变化曲线Fig.2 Inversion results of H model in survey station of a1, with the change curve of misfit and regularization factor

采用相同H型模型测点a2反演结果如图3所示，通过6次反演迭代，获得了较为理想的反演模型，模型响应也拟合得较好。

H型最终反演结果非常接近真实模型，低阻层的深度基本相当，中间层低电阻率接近真实值，测点a1反演结果第一层和第三层高阻也与真实值一致；测点a2接近大定源装置观测的极限位置，由于采用中心回线反演方式，对第一层高阻层的反应不够准确。

为了验证该反演算法对高阻层的反应能力，采用三层K型地电结构(各层参数如下:ρ1=50 Ω·m、ρ2=300 Ω·m、ρ3=50 Ω·m，层厚分别为100 m、100 m)进行验证。

图4所示是K型地电模型测点a1的反演结果，由于第一层低阻层的屏蔽作用，反演需要11次迭代才得到了较好的反演结果，基本反映出了真实的电阻率和深度，高阻层电阻率基本接近真实模型。采用相同的地电模型，测点a2的反演结果如图5所示。罗延钟(罗延钟等，2003)的正演研究结果表明，由于低阻层的屏蔽作用，瞬变电磁法对高阻层响应非常微弱，所以也导致对高阻层的反演需要较多的迭代次数；强建科(强建科等，2013)采用OCCAM方法对航空瞬变电磁反演的K型模型结果也证明，瞬变电磁法对高阻层的反演不够灵敏，基本无法反演出真实的高阻电阻率。

从图4、图5所示的响应拟合曲线、相对拟合差和正则化因子变化曲线，可以看出随着迭代次数增加，反演过程快速而稳定。本文的自适应正则化算法，由于采用了最光滑模型约束，对K型地电模型反演结果有很好的改善。

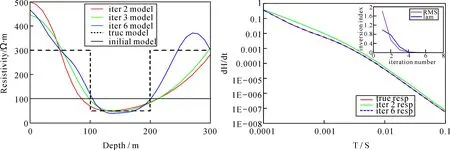
图3 H型模型测点a2反演结果以及拟合差、正则化因子变化曲线Fig .3 Inversion results of H model in survey station of a2, with the change curve of misfit and regularization factor

3.2 四层模型反演试算

由于大地构造的复杂性(毛立峰等，2011)，本文设计了四层HK型地电模型来验证本文算法的有效性。图6所示HK型地电模型(其中ρ1=200 Ω·m、ρ2=50 Ω·m、ρ3=250 Ω·m、ρ4=100 Ω·m，层厚分别为100 m、100m、100m)测点a2处的反演结果，无论是深度位置还是电阻率值与理论模型都拟合得较好；还是由于低阻层的屏蔽作用，相近的高阻层无法反映出真实的电阻率值，但是与周围地层电阻率的差异基本反映了出来。图6所示响应拟合曲线、数据拟合情况、正则化因子变化，说明了该反演算法的有效性和对复杂地电结构的适应性。

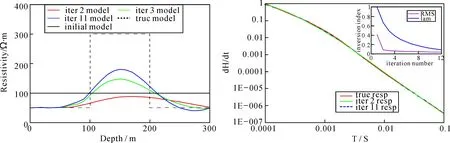
图4 K型模型测点a1反演结果以及拟合差、正则化因子变化曲线Fig.4 Inversion results of K model in survey station of a1, with the change curve of misfit and regularization factor

图5 K型模型测点a2反演结果以及拟合差、正则化因子变化曲线Fig .5 Inversion results of K model in survey station of a2, with the change curve of misfit and regularization factor

图6 四型模型测点a2反演结果以及拟合差、正则化因子变化曲线Fig.6 Inversion results of four layers model in survey station of a2, with the change curve of misfit and regularization factor

4 结论

本文实现了大定源回线瞬变电磁资料的一维自适应正则化反演，正则化因子的自适应调整，是该方法快速而稳定的收敛；由于采用最光滑模型约束模型目标函数，对于瞬变电磁法对高阻层反应不够灵敏的情况有所改善；对于复杂地电结构，该方法也有较好的有效性和适应性；并且反演迭代10次左右，就能够快速稳定的收敛，可以得到较为满意的结果，验证了该方法对于一维大定源回线瞬变电磁资料解释是可行的。

尽管利用自适应正则化反演算法进行大定源瞬变电磁一维反演具有诸多优点,但其亦存在不足。就算法本身而言，对于靠近发射线框区域测点，也采用中心回线反演方法近似处理，对于浅部地层的反演结果不够准确，同时瞬变电磁方法本身对相对高阻层的反应也不够灵敏，但是本文采用的反演方法基本可以达到预期的效果。

Anders V C, Niels B C. 2003.A quantitative appraisal of airborne and ground-based transient electromagnetic(TEM) measure events in Denmark[J].Geophysics,68(2):523-534

Alan Y L, James M, Andrea V. 2010.Breaks in lithology :Interpretation problems when handing 2D structures with a 1D approximation[J].Geophysics, 70(4):179-188

Brodie R, Sambridge M. 2006.A holistic approach to inversion of frequency-domain airborne EM data[J]. Geophysics,71(6): 301-312

Christensen N B, Reid J E, Halkjmr M.2009.Fast laterally smooth inversion of airborne time-domain electromagnetic data[J] .Near Surface Geophysics, 7(5):599-612

Chen Xiao-bin, Zhao Guo-ze, Tang Ji, Zhan Yan, Wang Ji-jun. 2005. An adaptive regularized inversion algorithm for regularized data[J]. Chinese Journal of Geophysics, 48(4): 937-946(in Chinese with English abstract)

Constable S C, Parker R L, and Constable. 1987. Occam’s Inversion: A practical algorithm for generating smooth models from electro sounding data[J]. Geophysics, 5(2):289-300

Deszcz Pan M，Fitterman D V, Labson V F. 1998.Reduction of inversion errors in helicopter EM data using auxiliary information[J].Exploration Geophysics, 29(2):142-146

Huang H, Palacky G J. 1991.Damped least-squares inversion of time-domain airborne EM data based on singular value decomposition[J]. Geophysical Prospecting, 39(6):827-844

Li Xiu. 2002. The theory and application of transient electromagnetic sounding. Xian: Shanxi Science and Technology Press:35-42(in Chinese)

Luo Yan-zhong, Zhang Sheng-ye, Wang Wei-ping. 2003. A research on one dimension forward for aerial electromagnetic method in time domain[J] .Chinese Journal of Geophysics,46(5): 719-724(in Chinese with English abstract)

Misac N N. 1992.Ectromagnetic Methods in Applied Geophysics [M].Zhao Jing-xiang tran.Beijing:Geological Publishing House: 195-207(in Chinese)

Misae N.Nabihgina. 1979. Quasi-static transient Response of a conducting half-space approximate presentation [J].Geophysics,Vol.44: 10-14

Mao Li-Feng, Wang Xu-ben, Chen Bin. 2011.Study on an adaptive regularized 1D inversion method of helicopter TEM data [J].Progress in Geophysics, 20 (1):300-305(in Chinese with English abstract)

Piao Hua-rong . 1990. The theory of electromagnetic sounding [M]. Beijing: Geological Publishing House :15-21(in Chinese)

Qiang Jian-ke, Li Yong-xing, Long Jian-bo. 2013.1-d Occam inversion method for airborne transient electromagnetic data[J]. Computing Techniques for Geophysical and Geochemical Exploration, 53(3):01-05(in Chinese with English abstract)

Sattel D. 2005.Inverting airborne (AEM) data with Zohdy ’s method[J].Geophysics, 70(4):77-85

Vallee M A, Smith R S. 2009. Application of Occam’s inversion to airborne time-domain electromagnetic [J].The leading Edge，28(3):284-287

Weng Ai-hua.2007. Occam’s inversion and its application to transient electromagnetic method [J]. Geology and Exploration,43(5):74-76(in Chinese with English abstract)

Yin C, Hodges G. 2007.Simulated annealing for airborne EM inversion [J].Geophysics, 72(4):189-195

[附中文参考文献]

朴化荣.1990.电磁测深法原理[M].北京：地质出版社:15-21

李 貅．2002.瞬变电磁测深的理论与应用[M]．西安：陕西科学技术出版社:35-42

翁爱华. 2007.Occam反演及其在瞬变电磁测深中的应用[J].地质与勘探, 43(5)：74-76

米萨克N.纳比吉安.1992.勘查地球物理-电磁法[M].赵经祥译.北京：地质出版社:195-207

陈小斌，赵国泽,汤 吉,詹 艳，王继军．2005.大地电磁自适应正则化反演算法[J]．地球物理学报,48(4)：937-946

罗延钟,张胜业,王卫平．2003.时间域航空电磁法一维正演研究[J]．地球物理学报,46(5)：719-724

强建科，李永兴，龙剑波.2013.航空瞬变电磁数据一维Occam反演[J]．物探化探计算技术,53(3)：01-05

毛立峰，王绪本，陈 斌．2011.直升机航空瞬变自适应正则化一维反演方法研究[J]．地球物理学进展，20(1)：300-305

One-Dimensional Adaptive Regularization Inversion of Transient Electromagnetic Sounding with a Large Fixed Source

XU Yu-cong1, ZHAO Ning2, QIN Ce1, WANG Rui1, ZHANG Zhao-bing1

(1.CollegeofGeophysics,ChengduUniversityofTechnology,Chengdu,Sichuan610059； 2.CollegeofComputerScienceandTechnology,HenanPolytechnicUniversity,Jiaozuo,Henan454000)

Adaptive regularization inversion has less requirement of the initial model, and directly inverts transient electromagnetic response data. In the 1D inversion algorithm, regularization factors are adaptively obtained by calculating the data object function and model object function in each iteration, so that the geoelectric structure in the subsurface can be quickly determined. This paper adopts the adaptive regularization inversion to compute an one-dimensional layered model of transient electromagnetic sounding with a large fixed source loop, using a homogeneous half-space model as the initial model. The model object function is employed to the depth of the second derivative of tiny model constraints for the first time. By calculating the typical theory model, the result of inversion fits very well and has high precision. Furthermore, avoiding repeated search for regularization factors, this method has fast convergence and shows good stability and reliability.

TEM, large fixed source, adaptive regularized inversion, smoothest constraint model

2014-09-19；

2014-12-16；[责任编辑]郝情情。

国家自然科学基金重点基金(U1262206)资助。

徐玉聪(1988年-)，男，在读硕士研究生，主要从事电磁法数值模拟。E-mail: xuyc1988@foxmail.com。

P618

A

0495-5331(2015)02-0360-06