基于频率域小波去噪的大地电磁信号工频干扰处理

蔡剑华,李 晋

(1. 湖南文理学院信息研究所,湖南常德 415000； 2. 湖南师范大学物理与信息科学学院, 湖南长沙 410081)



基于频率域小波去噪的大地电磁信号工频干扰处理

蔡剑华1,李 晋2

(1. 湖南文理学院信息研究所,湖南常德 415000； 2. 湖南师范大学物理与信息科学学院, 湖南长沙 410081)

大地电磁测深(Magnetotelluric，MT)在油气勘查中得到越来越多的应用，针对MT中日益严重的工频干扰，从频率域着手，结合小波阈值去噪方法，提出了基于频率域小波去噪的MT信号工频干扰处理方法。先对受噪的MT信号进行傅里叶变换，得到其实部和虚部，再用小波阈值去噪的方法对实部序列和虚部序列分别进行去噪处理，最后将去噪后的实部和虚部联合，进行反傅里叶变换得到去噪后的信号。给出了去噪方法的原理、步骤，并用仿真信号和实测大地电磁信号验证了其有效性。结果表明：频率域小波阈值去噪的大地电磁信号工频干扰处理方法是正确、有效的，能有效且自适应地压制大地电磁信号中的工频干扰，突出被工频干扰淹没了的有用信号的信息。

频率域 小波阈值 大地电磁信号 去噪

Cai Jian-Hua, Li Jin. Suppression of power line interference on MT signals based on the frequency domain wavelet method[J]. Geology and Exploration, 2015, 51(2):0353-0359.

近年来大地电磁测深得以迅速地发展，广泛应用于石油天然气勘查(孙卫斌等，2003)。在复杂山区的油气勘探应用效果日益突出，特别是在地震勘探困难区，油气电磁法勘探技术已成为首选的非地震勘探技术之一。油气勘探中利用电磁测深法，可以查明断裂，断裂破碎带，地质构造填图，岩层孔隙率调查及火成岩地质体等方面(卫平生等，2006; 王斌等，2014)。而大地电磁信号极其微弱，易受到噪声的污染，尤其是近些年来，随着国民经济和现代化建设的发展，电磁背景噪声日益严重，纵横交错的高压线、铁路电网、大型工业设备等造成的工频干扰成了大地电磁信号检测中难以避开的噪声来源(王书明等，2004;郭晓东等，2009)。小波去噪、经验模态分解、形态滤波等方法为抑制工频干扰提供了有利的手段，取得了不错的效果(严家斌等，2008；汤井田等, 2008)。尤其是小波方法，自上世纪80年代应用于地球物理领域来得到了很大的发展，被成功应用在大地电磁信号的去噪、谱估计和静态效应抑制等方面(Tradetal, 2000; 严家斌等，2008)。常规的小波去噪，通常是在时间域对信号进行分解，再对分解得到的系数进行阈值去噪，最后再重构达到去噪的目的(徐宏斌等，2012;陈涛等,2013)。本文从频率域着手，提出了基于频率域小波去噪的大地电磁信号工频干扰处理方法，先对受噪的MT信号进行傅里叶变换，得到其实部和虚部，再用小波阈值去噪的方法对实部序列和虚部序列分别进行去噪处理，最后将去噪后的实部和虚部联合，进行反傅里叶变换得到去噪后的信号。试图为大地电磁信号去噪探索新的技术手段。

1 基本原理

1.1 傅里叶变换和反变换

给定实自变量t的非周期函数f(t)，可以是实函数，也可以是复函数，做积分

(1)

若上式对参数ω的任何实数值都存在， 则称F(ω)为f(t)的傅里叶变换， 或称傅里叶积分。f(t)可用F(ω)的积分表示，称为傅里叶逆变换。

(2)

离散时间信号x(n)的连续傅立叶变换定义为

(3)

式中X(ejω)是一个连续函数，不能直接在计算机上做数字运算。为了在计算机上实现频谱分析，必须对x(n)的频谱作离散近似。有限长离散信号的离散傅立叶变换定义为

(4)

式中ωN=exp(-j2π/N)，其反变换定义为

(5)

工程上都通过构造离散傅里叶变换的快速算法，即快速离散傅里叶变换来实现傅氏变换。傅里叶变换的振幅谱、相位谱和能量谱分别为(孙丽颖等，2005)

(6)

(7)

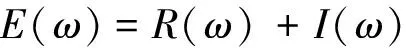
(8)

式中R(ω)，I(ω)分别表示傅里叶变换的实部和虚部。

1.2 小波阈值去噪

对于连续的情况，小波为(Mallatetal,1992; Donohoetal,1994)

(9)

式中：Ψa,b(t)为一个基本小波函数或母小波函数，a为伸缩(尺度) 因子；b为平移因子。任给函数f(t) ∈L2(R)，其连续小波变换及重构公式(逆变换) 为

(10)

(11)

对于离散情况，小波为(Donohoetal,1994,1995)

(12)

与函数f(t) 相应的离散小波变换系数及其重构公式为

(13)

(14)

式中：C是一个与信号无关的常数。根据小波变换的Mallat算法，对信号其进行分解，得到不同尺度上的小波系数Cj,k，再对Cj,k进行阈值处理，然后再进行重构得到新信号。本文采用常用的软阈值算法如下(Donohoetal,1995; Johnstoneetal,1997):

(15)

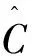
(16)

其中，N为信号长度，σ为噪声的方差(Donohoetal,1995)

σ=MADj/0.6745

(17)

MADj为小波分解后第j层高子带系数的中值。

2 去噪流程

基于频率域小波去噪的MT信号工频干扰处理流程如图1所示：(1) 通过Fourier变换将原始含噪的大地电磁信号变换到频率域中，得到信号傅里叶变换的实部和虚部；(2) 对实部和虚部分别进行小波变换，并对各层系数进行小波软阈值处理；(3) 将处理后的实部和虚部分量组合成新的复数序列；(4) 最后通过反Fourier变换将此序列转换至时间域，达到在频率域用小波阈值方法抑制大地电磁信号噪声的目的。

3 仿真处理

仿真信号用蒙特卡洛方法产生互不相干的一组随机信号，噪声为类似实际信号采集中常见工频干扰的正弦信号，幅值为仿真信号最大值的1.2倍，频率为50 Hz。原始仿真信号和加噪后仿真信号的时域图如图2(a)和图2(b)所示。显然，由于正弦噪声干扰的加入，仿真信号完全被覆盖，整体表现为正弦波的形态，从时域无法看出信号的细节特征。加噪前后仿真信号的统计参数为：加噪前信号的方差为480.7422，能量为4.8069×105mV2；加噪声后信号方差为3.630×103，能量为3.6269×106mV2，信噪比为-8.9075 dB。图3(a)、图3(b)、图3(c)分别给出了仿真信号、所加的噪声信号和加噪后信号的时频谱图和边际谱图。从时频谱图可以看到，噪声的能量非常强，在图3(c)中，加入的噪声能量几

图1 频率域小波去噪的流程图Fig.1 Flow chart of de-noising based on frequency domain Wavelet

乎淹没了其他频率成分的信息。

图2 去噪前后的仿真信号Fig.2 Simulated signal of before and after de-noisinga-无噪仿真信号; b-加噪后仿真信号; c-去噪后仿真信号a-original signal; b-noised signal; c-de-noised signal

按照本文提出的方法，对含噪信号进行去噪处理，先对加噪后的信号进行快速傅里叶变换，得到其实部和虚部，再用小波阈值去噪的方法对实部序列和虚部序列分别进行去噪处理(本文采用小波软阈值去噪方法，阈值函数如公式(15)，阈值如公式(16)所示)，最后将去噪后的实部和虚部联合，进行反傅里叶变换得到去噪后的信号。去噪声后信号的方差为482.0253，能量为4.8150×105mV2，信噪比为16.5859 dB。可见，噪声能量得到了有效的抑制，信号能量由去噪前的3.6269×106mV2降到了4.8150×105mV2，而去噪后信号的能量基本与原始信号能量4.8069×105mV2，保持相当。图2(c)为信号去噪后的时域图，图3(d)为信号去噪后的时频图，我们分别将他与其对应的图2(a)和图3(a)比较，可以看出信号和频谱形态基本恢复了原样。显然，从图谱和统计参数上都可以看出，本文提出的基于频率域小波去噪的方法能有效去除50 Hz的干扰信号。

4 实测信号处理

周期正弦噪声往往由观测点附近高压线或其他大型工业电器设施产生，由于强度大，在时间序列主要表现为正弦波的形式，它几乎完全掩盖了电磁信号，形成拟等振幅的50 Hz 噪声干扰。具有如下表达形式

(18)

其Fourier 变换形式为：

(19)

实测数据是来自安徽某矿区某测点的EH-4数据，作业区离矿区很近，有多条高压电线跨过。图4所示为典型的受工频干扰大地电磁信号的时间序列，从图4可以看出：在强正弦噪声干扰下，天然电磁场信号完全被掩盖，在时间序列上很难识别出天然电磁信号的存在。为作去噪前后的对比，先给出信号去噪前的统计参量为：Hy分量最大值为1.4676×104nT，最小值-1.4152×104nT，方差为3.3915×107，能量为1.3911×1011nT2；Ex分量最大值为 631 mV，最小值-770 mV，方差为5.1922×104，能量为2.2192×108mV2；Hx分量最大值为1.2560 ×104nT，最小值-1.2753×104nT，方差为2.7146×107，能量为1.1123×1011nT2；Ey分量最大值为4.998 ×103mV，最小值-5.236×103mV，方差为3.5392×106，能量为1.4493×1010mV2。由于极化方向的原因，这类干扰可能在某个方向上强度较大，在另一个方向上强度较小，对单一主频的噪声往往只对其主频和谐波频率上的阻抗计算产生较大的影响。

图3 去噪前后仿真信号的时频谱图Fig.3 Time-frequency spectrum of simulated signal of before and after de-noisinga-无噪仿真信号；b-所加噪声；c-加噪后仿真信号；d-去噪后仿真信号a-Original signal；b-Noise；c-Noised signal；d-De-noised signal

图4 实测大地电磁信号时域图Fig.4 Time-frequency spectrum of measured MT signal

图5所示为4道信号去噪前后所对应的功率谱。功率谱能很好地区分出能量随频率的细微变化，能反应大地电磁信号每频段的频率特性和能量差异。由图5(左)去噪前的功率谱和时频谱可以清晰的看到，50 Hz频点及其谐波成分处的信号能量极大，是其他频率成分的好几倍，几乎掩盖了其他信号的信息。为作对比，图5(右)给出了传统小波阈值去噪的结果，从图中可以看出，50 Hz工频干扰的幅值很大程度上得到了有效抑制，但还能看到此频点出突出的幅值。采用本文提出的去噪方法，对各道信号进行去噪处理。图5(中)所示为4道信号去噪后所对应的功率谱。与图5左右两边的谱图对比，可以看出：本文方法去噪后50 Hz的工频干扰及其低频段部分工频干扰的谐波成分也得到了有效的抑制，且本文提出的去噪方法也较传统的小波阈值去噪效果好。

图6所示为4道信号去噪后信号的时域图，消噪后信号的统计参量：Hy分量最大值为2.8016×103nT，最小值为-2.6927×103nT，方差为8.6367×105，能量为3.5368×109nT2；Ex分量最大值为173.7995 mV，最小值为-156.8419 mV，方差为1.4768×103，能量为6.0478×106mV2；Hx分量最大值为2.9489×103nT，最小值为-2.5824×103nT，方差为8.2590×105，能量为3.3821×109nT2；Ey分量最大值1.7922×103mV，最小值为-1.3696×103mV，方差为 2.1610×105，能量为 8.8495×108mV2。对比去噪前后的统计参数，4道信号的方差和能量都减小了，磁道信号方差和能量强度下降了2个数量级，电道信号方差和能量强度下降了1个数量级，这也与工频干扰主要影响磁道信号的事实相符。由去噪前后的统计参数，结合前面分析的功率谱，可以看到：消噪后信号显得较为平稳，看不到周期波形，信号形态符合大地电磁信号的规律，突出了被噪声掩盖的有用信息，这就为后续的功率谱估计和阻抗估算提供了条件。

图5 去噪前后大地电磁信号的功率谱(左为去噪前的，中为本文方法去噪后的，右为传统小波方法去噪后的)Fig.5 Power spectrum of measured signal of before and after de-noising(the left is before de-noising, the middle is after de-noising based on presented method, the right is after de-noising based on traditional Wavelet method)a-Hy分量；b-Ex分量；c-Hx分量；d-Ey分量；a-Hy component；b-Ex component；c-Hx component；d-Ey component

进一步，用去噪前后的信号计算其功率谱，并估算了视电阻率曲线和相位曲线，结果如图7所示。

去噪前后响应曲线的整体趋势是一致的，但细节上发现了明显的变化。由去噪前的曲线可以看到，由于受到强烈的工频干扰，在50 Hz频点处，视电阻率曲线和相位曲线参数都存在飞点，而去噪后响应曲线变得平滑，曲线突变点得到有效抑制，MT测深资料的质量得到了提高了。

图6 消噪后实测大地电磁信号的时域图Fig.6 Time domain wave of measured MT signal after de-noising

5 结论

日益严重的工频干扰给大地电磁信号检测带来了麻烦，这类干扰可能在某个方向上强度较大，在另一个方向上强度较小，对视电阻率和相位等MT响应参数的计算产生较大影响。本文从频率域着手，结合小波阈值去噪方法，提出了基于频率域小波去噪的大地电磁信号工频干扰的抑制方法，仿真和实测信号的处理验证了方法的有效性。结果表明本文方法突出了被工频干扰淹没了的有用信号的信息，这就为后续的功率谱估计和阻抗估算提供了条件，为大地电磁信号去噪提供了新的技术手段。

图7 消噪前后的大地电磁响应曲线对比Fig.7 Comparison of MT response curve before and after de-noisinga-ρxy曲线；b-ρyx曲线；c-Фxy曲线；d-Фyx曲线a-ρxy curve；b-ρyx curve；c-Фxy curve；d-Фyx curve

Cai Jian-hua, Wang Xian-chun, Hu Wei-wen.2013.De-noising of MT signal based on empirical mode decomposition and wavelet threshold method[J]. Geophysical Prospecting, 2013, 48(2):303-307 (in Chinese with English abstract)

Chen Tao, Wang Wei, Ji-qing. 2013. De-noising method of fiber gyro signal based on wavelet transform[J] . Ordnance Industry Automation, 32(3):70-71,82( in Chinese with English abstract)

Donoho D L.1995. De-noising by soft-thresholding[J]. IEEE Transaction on Information Theory, 41(3):613-627

Donoho D L, Johnstone I M. 1994. Ideal spatial adaptation via Wavelet shrinkage[J]. Biometrika, 81:425-455

Johnstone L M and Silverman B W.1997.Wavelet threshold estimators for data with correlated noise[J]. J R Statist Soc,59(B):319-351

Guo Xiao-dong, Chen Xiao-qiang, Wang Zhi-hua, Cheng Rui-lin, Fan Zhan-jun, Xu De-li. 2009. Application of EH4 continuous conductivity measure in Baoxingchang district[J]. Geology and Prospecting, 45(1):52-58(in Chinese with English abstract)

Sun Li-yin, Qu D, Yan T. 2005. Application of Fourier Transform and Wavelet Transform to Signal Fault Diagnosis[J]. Journal of Liaoning Institute of Technology, 25(3): 155-157( in Chinese with English abstract)

Mallat S, Hwang W L.1992.Singularity detection and processing with Wavelet[J]. IEEE Transation on Information Theory,38(2):617-643

Sun Wei-bin, Song Qun-hui, Zheng Li. 2003. The development of MT sounding technique and its application to the oil and gas exploration[J].Geology and prospecting, 39(10): 1-7 ( in Chinese with English abstract)

Trad D O, Travassos J.M. 2000. Wavelet filtering of magnetotellurie data[J]. Geophysics, 65: 482-491

Tang Jin-tian, Hua Xi-rui, Cao Zhe-min. 2008. Hilbert-Huang transformation and noise suppression of magnetotelluric sounding data[J]. Chinese J. Geophys, 51(2): 603-610(in Chinese with English abstract)

Wei Pin-sheng, Tan Kai-jun, Zhang Hu-quan. 2006. Application of magnetotelluric sounding to oil and gas exploration: Take the Minghe basin as an example[J]. Natural gas industry, 26 (8):37-40 (in Chinese with English abstract)

Wang Bin,Chen Xiao-qiang, Fan Zhan-jun, Chen Rui-lin. 2014. Application of EH4 continuous conductivity meter to the study of ore-controlling structures in the Jinlongshan gold deposit of Zhen’an country,Shaanxi Province [J]. 50(3): 0564-0571 (in Chinese with English abstract)

Wang Shu-min, Wang Jia-yin. 2004. Analysis on statistic characteristics of Magnetotelluric signal[J]. Acta Seismologica Sinica, 26 (6):669-674( in Chinese with English abstract)

Xu Hong-bin, Li Shu-lin, Chen Ji-jing. 2012. A study on method of signal de-noising based on wavelet transform for micro-seismicity monitoring in large-scale rockmass structures[J]. Acta Seismologica Sinica, 34(1): 81-96( in Chinese with English abstract)

Yan Jia-bin, Liu Gui-zhong, Liu Jian-xin. 2008. Application of wavelet transform in processing nature electromagnetic field time series[J]. Geology and Prospecting, 44(3): 75-78( in Chinese with English abstract)

[附中文参考文献]

蔡剑华, 王先春, 胡惟文. 2013. 基于经验模态分解与小波阈值的MT信号去噪方法[J]. 石油地球物理勘探,48(2):303-3070

陈 涛,王 伟,吉 清. 2013. 基于小波变换的光纤陀螺信号去噪方法[J]. 兵工自动化, 32(3):70-71,82

郭晓东,陈孝强,王治华,陈瑞林,樊占军,徐德利. 2009. EH4 连续电导率测量在宝兴厂矿区的应用[J]. 地质与勘探,45( 1) : 52-58

徐宏斌, 李庶林, 陈际经. 2012. 基于小波变换的大尺度岩体结构微震监测信号去噪方法研究[J]．地震学报,34(1):81-96

孙卫斌, 宋群会, 郑 莉. 2003.大地电磁测深技术发展及在油气勘探的应用[J]. 地质与勘探, 39(10):1-7

孙丽颖, 屈 丹, 闫 钿. 2005. 傅里叶变换与小波变换在信号故障诊断中的应用[J]. 辽宁工学院学报, 25 (3):155-157

汤井田, 化希瑞, 曹哲民. 2008. Hilbert-Huang变换与大地电磁噪声压制[J].地球物理学报, 51(2):603-610

卫平生,谭开俊,张虎权. 2006.大地电磁测深在油气勘探中的应用—以民和盆地为例[J]. 天然气工业, 26 (8):37-40

王 斌, 陈孝强, 樊战军,陈瑞林. 2014. EH4 连续电导率仪在陕西省镇安县金龙山矿区控矿构造研究中的应用[J]. 地质与勘探, (50)3: 0564-0571

王书明,王家映. 2004. 大地电磁信号统计特征分析[J].地震学报, 26(6) :669-674

严家斌, 刘贵忠, 柳建新. 2008.小波变换在天然电磁场信号时间序列处理中的应用[J]. 地质与勘探, 44(3): 75-78

Suppression of Power Line Interference on MT Signals Based on the Frequency Domain Wavelet Method

CAI Jian-Hua1, LI Jin2

(1.InstituteofInformation,HunanUniversityofArtsandScience,Changde,Hunan415000; 2.InstituteofPhysicsandInformationScience,HunanNormalUniversity,Changsha,Hunan410081)

The magnetotelluric(MT)method is widely applied in oil and gas exploration. While power line interference is an increasingly serious problem with the development of society. In the frequency domain, combined with the wavelet threshold method, an approach to restrain power line interference is proposed for MT signal processing. Firstly, the Fourier transform is applied to the noised MT signal and its real and imaginary parts can be obtained. Then, wavelet threshold method is used to de-noise for the imaginary and the real part sequences. Finally, the de-noised real and the de-noised imaginary are assembled, and the anti-Fourier transform is conducted and the de-noised signal is obtained. The principle and steps of de-noising methods are presented. The simulated signals and the measured MT data are processed to verify its validity. The results show that the proposed method is correct and effective. It can suppress the power line interference on MT signal effectively and adaptively, and the useful information is highlighted which is concealed by the power line interference.

Frequency domain, Wavelet threshold, Magnetotelluric signal, De-noising

2014-09-26；[修改日期]2014-12-28；[责任编辑]陈伟军。

国家自然科学基金项目(41304098，41404111), 湖南省自然科学基金项目(12JJ4034), 湖南省教育厅青年项目(13B076), 湖南省重点建设学科—光学基金, 湖南省重点实验室“光电信息集成与光学制造技术”,“湖南省光电信息技术校企联合人才培养基地”共同资助。

蔡剑华(1979年-), 男, 2010年毕业于中南大学，获博士学位, 副教授, 从事大地电磁数据处理的研究。E-mail:cjh1021cjh@163.com。

P361.4

A

0495-5331(2015)02-0353-07