基于市场划分的再制造闭环供应链模型

杨爱峰， 陈 骜， 胡小建

（合肥工业大学 管理学院，安徽 合肥 230009）

0 引 言

近年来，再制造作为节能减排和发展循环经济的重要手段，越来越受到国家和企业的重视。文献［1－2］指出再制造可以降低废旧产品对环境的不良影响，减少原材料的消耗，而更重要的是再制造可以为企业节省成本、增加利润、提升企业竞争力。众多企业意识到再制造可能带来的巨大商机，开始采用制造与再制造相混合的生产模式，以确保企业在竞争中处于优势地位［3－4］。例如，世界上最大的重型机械生产商之一卡特彼勒，目前在全球包括中国在内的8个国家拥有19家再制造工厂，再制造废旧单体发动机多达220万件，其中85%的零部件均来自再制造或再利用，可节约金属6×104t以上，再制造产值在2011年已超过20亿美元。文献［5］对再制造的经济效益进行了评估，并且指出再制造是对经济产生重大且持久影响的棘手问题；文献［6］分析了再制造对宏观经济的影响，并且断言再制造会增加社会对劳动力的需求，同时可降低原材料的消耗。

从目前再制造产品市场研究现状来看，研究成果主要集中在新产品和再制造产品的定价问题上。文献［7］研究了当制造商和再制造商相互竞争时，制造商的定价与再制造策略；文献［8］以消费者对新产品的估值要高于对再制造产品的估价为基础，指出不同技术选择会影响这种估价，再通过制造商对再制造技术的选择和产品差异化定价细分市场；文献［9］通过建立数学模型，对比研究垄断市场和竞争条件下的再制造策略，并建议垄断者应采取恐吓策略来防止竞争者的进入；文献［10］进一步研究了单周期、两周期、多周期以及无限周期内，制造商在竞争市场中产品差异化定价决策问题；文献［11］通过模型研究当再制造产品的高端市场和低端市场之间存在需求的替代关系时，新产品和再制造产品的最优定价问题；文献［12］研究了制造商回收、零售商回收和第三方回收的3种情况下两阶段闭环供应链中的产品定价问题；文献［13］建立集成式供应链和分散式供应链模型，研究在政府对再制造进行补贴情况下的最优批发价格和生产数量；文献［14］建立两阶段和多阶段的优化模型，研究了新产品和再制造产品的多阶段静态和动态定价问题。

本文以顾客对新产品和再制造产品的估值差异为基础将市场划分，研究在不同市场环境中的最优定价策略，探索顾客对产品估值变化对产品定价和企业利润的影响。本文在前人的基础上，进一步讨论了存在零售商和独立制造商的分散闭环供应链模型中新产品和再制造产品的零售价格和批发价格最优定价策略，最后通过数值算例分析顾客对再制造产品接受度和节约成本对分散供应链利润影响，并比较分散供应链和集中供应链的总利润。

1 模型符号和假设

本文以闭环供应链为研究对象，分别讨论了市场划分情况下进行再制造活动和无再制造活动的最优定价策略。

本文用到的参数如下：Q为市场潜在需求量；qn为新产品需求量；qr为再制造产品需求量；cn为单位新产品的制造成本；cr为单位再制造产品的制造成本；Δ为单位再制造产品的节约成本（Δ＝cn－cr）；θ为顾客对再制造产品接受度（0＜θ＜1）；αn为顾客对新产品的估值；αr为顾客对再造产品的估值；Un为新产品对顾客的效用；Ur为再制造产品对顾客的效用。

决策变量如下：pn为单位新产品的零售价格；pr为单位再制造产品的零售价格；wn为单位新产品的批发价格；wr为单位再制造产品的批发价格。

本文做假设H1～H7。

H1：单位新产品的制造成本要高于单位再制造产品的制造成本，即cn＞cr。并且不考虑回收的废旧品质量差别，所有的再制造产品的成本均为cr，其中cr包含废旧产品的回收成本。

H2：顾客愿意为产品支付的价格范围是［0，Q］，且cn＜Q。

H3：顾客对新产品的估值αn∈［0，Q］，且αn服从均匀分布U［0，Q］，即密度函数是f（αn）＝1／Q；顾客对再制造产品的估值αr＝θαn。

H4：供应链活动中所有参与者均是风险中性的。

H5：供应链中所有参与者的决策活动都在1个周期内进行。

H6：在周期开始前，市场中存在足够多的废旧产品。

H7：不考虑交易时间和生产时间。

引理1 当市场中存在新产品和再制造产品时，新产品的需求量，再制造产品的需求量

证明 根据H3，可以得到新产品和再制造产品对顾客的效用分别为：

（1）当顾客愿意购买新产品时，即Un＞Ur，可以得到：

又

因此消费者愿意购买新产品的数量为：

（2）当顾客愿意购买再制造产品时，即Un＜Ur，可以得到：

又只有当再制造产品对顾客的效用非负时，顾客才愿意购买再制造产品，可以得到：

因此消费者愿意购买再制造商品的数量为：

综上所述，引理1得证。

2 无再制造活动的供应链模型（NR）

在NR模型中，由于制造商不进行再制造活动，市场中仅有新产品，其供应链结构如图1所示。

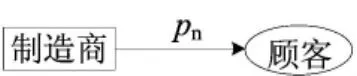
图1 NR模型的供应链结构

制造商的函数为：

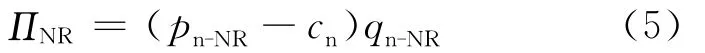
新产品的需求量为：

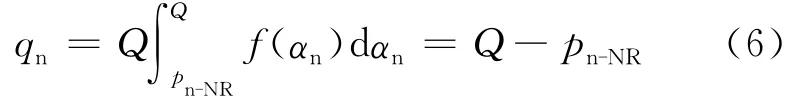
证明 将（6）式带入（5）式得到：

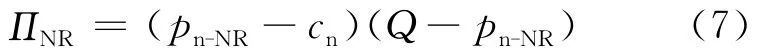
分别对（7）式求pn－NR的一阶导数和二阶导数，可得：

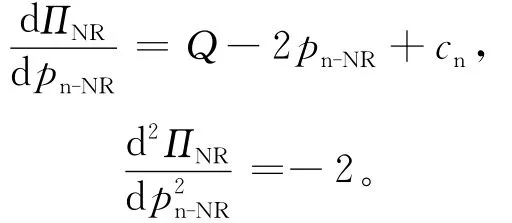
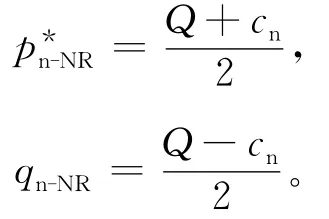
综上所述，命题1得证。

3 有再制造活动的集中供应链模型（CR）

在CR模型中，市场中仅有1个垄断制造商，并且承担产品的零售工作。在周期开始时制造商从顾客手中回收废旧产品，并同时生产新产品和再制造产品，最后同时投入市场。其闭环供应链结构如图2所示。

图2 CR模型的供应链结构

根据模型假设，制造商的利润为：

其中，（pn－CR－cn）qn－CR为制造商零售新产品所获得的利润；（pr－CR－cr）qr－CR为制造商通过再制造所获得的利润。命题2 在CR模型中，新产品的最优零售价格为＝（Q＋cn）／2，再制造产品的最优零售价格为＝（θQ＋cr）／2，此时新产品的需求量为：

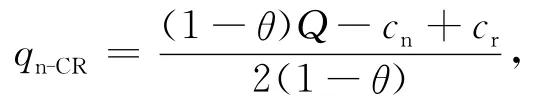
再制造产品的需求量为：

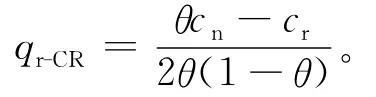
证明 将（3）式、（4）式带入（8）式可得：

分别对（9）式中的pn－CR、pr－CR求一阶偏导数，可得：

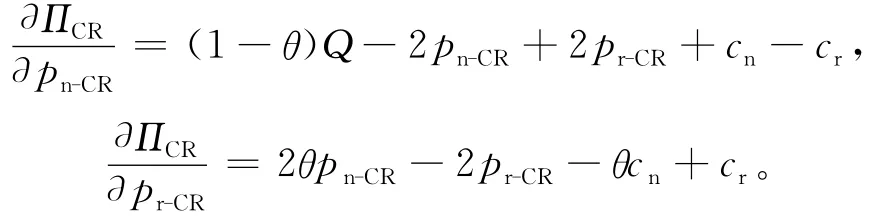
求解（9）式的Hessian矩阵可得：

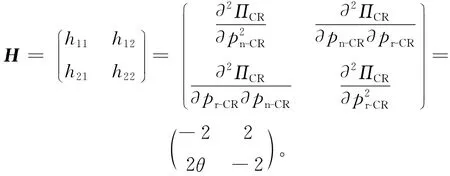
显然，h11＜0，｜H｜＞0。所以 Hessian矩阵负定，即存在唯一解使得（9）式取得最大值。

将（10）式、（11）式带入（3）式、（4）式可得：

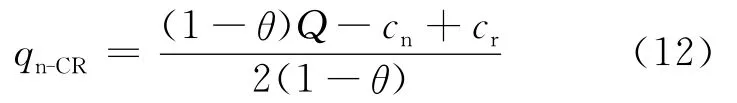
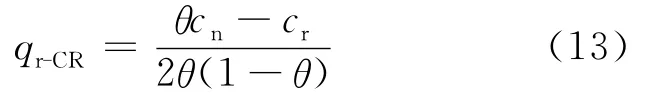
综上所述，命题2得证。

推论1 在CR模型中，当且仅当θcn＞cr时，制造商才能通过再制造活动获得利润。

4 存在零售商的再制造供应链模型（DR）

在DR模型中，制造商和零售商是独立决策者，两者进行Stackelberg博弈，其中制造商为博弈的领导者，零售商为博弈的跟随者，其闭环供应链结构如图3所示。

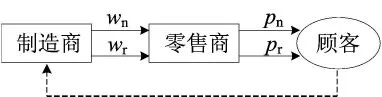
图3 DR模型的供应链结构

制造商的利润为：

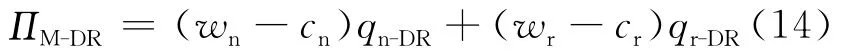
零售商的利润为：

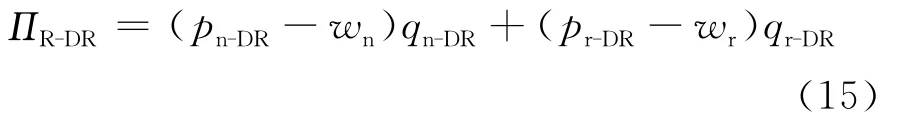
按照Stackelberg动态博弈逆向求解法求解该模型中制造商与零售商的最优价格策略。零售商作为跟随者，首先决策再制造产品与新产品的最优零售价格；制造商作为主导者，根据零售商的最优零售价格，确定最优批发价格。

命题3 在DR模型中，制造商给零售商提供新产品和再制造产品的最优批发价格为：

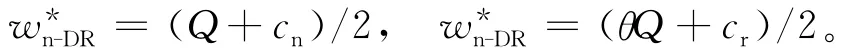
零售商将新产品和再制造产品投入市场的最优零售价格为：

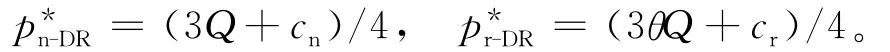
此时新产品和再制造产品的需求量为：

证明 类似于命题2。

5 存在独立再制造商的再制造OI模型

在OI模型中，市场中存在原始设备制造商（OEM）和独立再制造商（IO），两者相互竞争。OEM只生产新产品，需要决策新产品的零售价格；IO从顾客手中回收废旧产品并生产再制造产品，需要决策再制造产品的零售价格。OEM和IO之间是静态博弈的，其闭环供应链结构如图4所示。

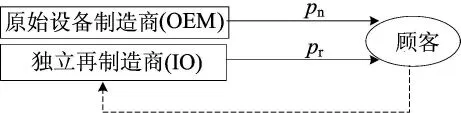
图4 OI模型的供应链结构

OEM的利润为：

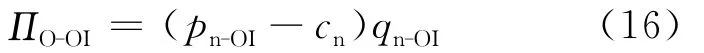
IO的利润为：

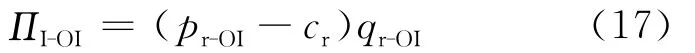
利用Nash静态博弈求解该模型中OEM与IO的最优价格决策。

OEM和IO同时决策新产品和再制造产品的零售价格。

命题4 在OI模型中，新产品和再制造产品的最优零售价格分别为：

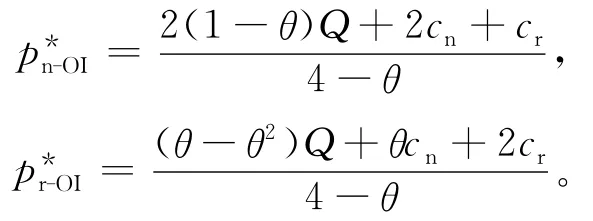
此时新产品和再制造产品的需求量为：

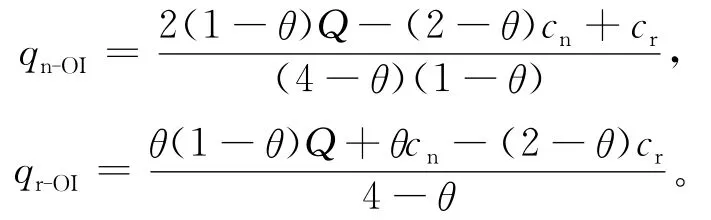
证明 将（3）式、（4）式带入（16）式、（17）式，可得：

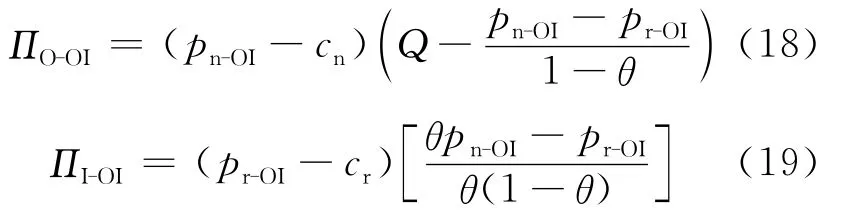
对（18）式中pn－OI和（19）式中pr－OI求一阶偏导和二阶偏导可得：

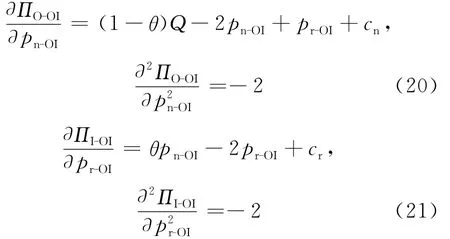
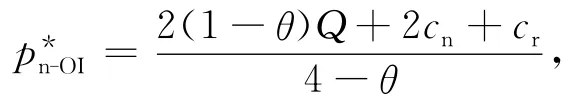
将pn－OI、pr－OI代入（3）式、（4）式可得：

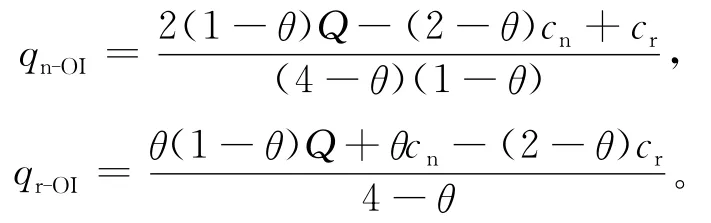
综上所述，命题4得证。

6 数值仿真

数值仿真参考文献［15］设定参数，运用Matlab2012编程得到结果。

6.1 θ变化时CR模型和NR模型利润比较

取Q＝1，cn＝0.1，Δ分别取 0.05、0.06、0.07，让θ在［0.5，0.7］变化，Δ和θ对CR模型和NR模型利润的影响如图5所示。

图5 Δ和θ对CR模型和NR模型利润的影响

由图5可知，在相同的接受度水平下，制造商销售再制造产品可以获得利润，并且随着节约成本的增加，制造商获得的利润呈现递增趋势；在节约成本水平相同时，制造商的利润随着顾客对再制造产品接受度的提升而提升。

6.2 DR模型和CR模型利润分析

（1）节约成本Δ和接受度θ对DR模型中制造商和零售商利润的影响。取Q＝1，cn＝0.1，cr分别取0.03、0.04、0.05，让θ在［0.5，0.7］变化，得到Δ和θ对DR模型中制造商和零售商利润的影响，如图6所示。

由图6可知，制造商和零售商的利润水平都随着接受度θ的增加而增加，并且当再制造成本越低时，制造商和零售商可以获得更高的利润。

（2）DR模型供应链总利润和CR模型比较。DR模型供应链总利润为：

取Q＝1，cn＝1，cr＝0.04，让θ在［0.5，0.7］变化，得到θ变化时DR模型和CR模型利润比较，如图7所示。

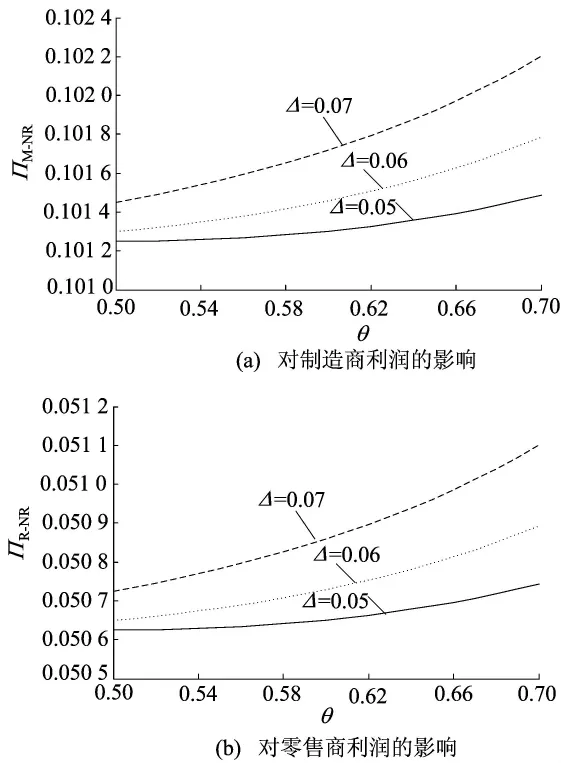
图6 Δ和θ对DR模型中制造商和零售商利润的影响

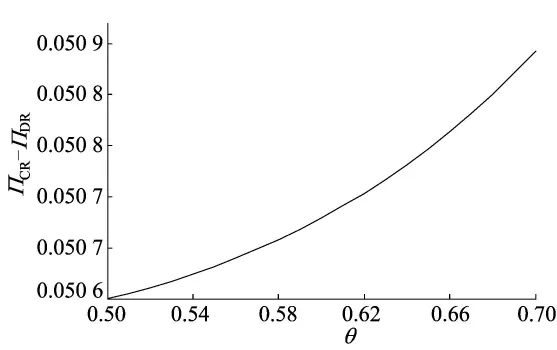
图7 θ变化时DR模型和CR模型利润比较

由图7可知，CR模型的总利润要高于DR模型的总利润，并且随着接受度θ的增加而增加。这是因为在DR模型中制造商和零售商存在竞争关系导致的利润流失。

6.3 OI模型和CR模型利润分析

（1）节约成本Δ和接受度θ对OI模型中制造商和再制造商利润分析。取Q＝1，cn＝0.1，cr分别取0.03、0.04、0.05，让θ在［0.5，0.7］内变化，得到Δ和θ对OI模型中OEM和IO利润的影响，如图8所示。

图8反映制造商的利润随着接受度θ和节约成本Δ的增加而减小，而再制造商的利润与接受度θ和节约成本Δ呈正比关系。这可以解释为，当θ增加时，顾客对再制造产品认可度提高，使得再制造产品的零售量提高，导致新产品的零售量降低。而Δ越高，对再制造商越有利，使得生产成本减少，从而再制造产品价格减少，达到薄利多销的效果，需求量提高。从而制造商的利润降低而再制造商获得了更高的利润。

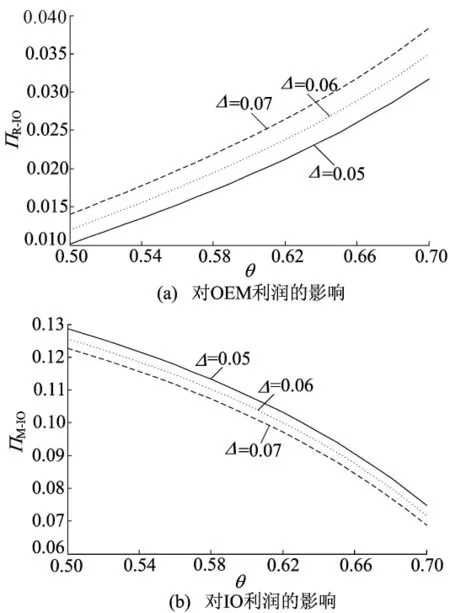
图8 Δ和θ对OI模型中OEM和IO利润的影响

（2）IO模型总利润与CR模型比较。IO模型供应链总利润为：

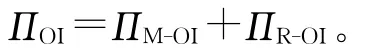
取Q＝1，cn＝1，cr＝0.04，让θ在［0.5，0.7］变化，得到θ变化时OI模型和CR模型利润比较，如图9所示。

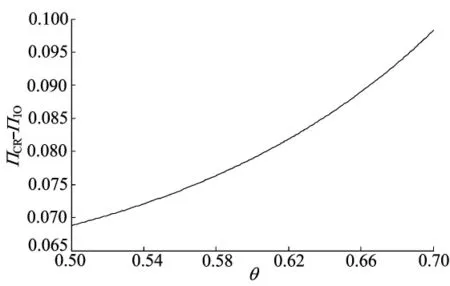
图9 θ变化时OI模型和CR模型利润比较

由图9可知，CR模型的总利润要高于OI模型的总利润，并且随着接受度θ的增加而增加。这是因为在OI模型中，制造商和再制造商为了追求各自最高利润，从而在竞争中造成利润流失，不能使供应链总利润达到最大。

7 结束语

废旧品回收再制造已经广泛应用到了汽车、家电和机械等行业，并取得良好的经济效益、环境效益和社会效益。面对激烈的市场竞争环境，国际上具有代表意义的施乐、GE、IBM、柯达、HP、Sears、3M和Ericsson等国际顶尖企业已经建立了自己相应逆向物流体系，并且都已成为增强竞争力、获取经济效益和社会效益的有力手段。以IBM为例，IBM专门设立了独立部门来管理、经营世界范围内的废旧产品和材料的回收再利用（CR模型），并且已经成为提升整体服务水品的有效竞争力，据统计单以回收租用到期的硬件的价值就占到整个硬件产值的35%，每年可节约成本700万美元。在我国，2010年汽车保有量超过8 000万辆，主要工程机械保有量300多万台，如利用零售商进行废旧产品回收再制造（DR模型），那么再制造产品的市场占有率达到配件市场的5%，就可以实现400亿元以上的产值［16］。

本文针对存在制造商回收废旧产品的闭环供应链，分别建立存在不同参与者的供应链模型，研究产品的最优定价策略（包括新产品的零售价、再制造产品的零售价和批发价）。最后，运用数值算例验证了本文的模型，并得出接受度和生产成本对供应链各成员利润的影响以及各供应链模型的总利润大小关系。本文的后续研究方向是考虑到在生产再制造产品时政府给予补贴以及考虑两阶段模型中由于回收废旧产品质量不确定性而导致再制造成本不确定性的情况。

［1］ Seitz M，Ken P.Meeting the closed－loop challenge：the case of remanufacturing ［J］.California Management Review，2004，46（2）：74－89.

［2］ Toktay L，Beril M.Zenios A.Inventory management of remanufacturable products［J］.Management Science，2000，46（11）：1412－1426.

［3］ Johnson M R，Wang M.Economical evaluation of disassembly operations for recycling，remanufacturing and reuse［J］.International Journal of Production Research，1998，36（12）：3227－3252.

［4］ Guide V，Daniel R，Wassenhove N.Closed－loop supply chains：an introduction to the feature issue：part 1［J］.Production and Operations Management，2006，15 （3）：345－350.

［5］ Ayres R，Ferrer G.Eco－efficiency，asset recovery and remanufacturing ［J］.Eur Management J，1997，15（5）：557－574.

［6］ Ferrer G，Robert U.The impact of remanufacturing in the economy ［J］.Ecological Economics，2000，32 （3）：413－429.

［7］ Majumder P，Groenevelt H.Competition in remanufacturing［J］.Production and Operations Management，2001，10（2）：125－141.

［8］ Debo L，Toktay B，Wassenhove N.Market segmentation and product technology selection for remanufacturable products［J］.Management Science，2005，51（8）：1193－1205.

［9］ Ferguson M E，Toktay L.The effect of competition on recovery strategies［J］.Production and Operations Management，2006，15（3）：351－368.

［10］ Ferrer G，Swaminathan M.Managing new and remanufactured products ［J］.Management Science，2006，5（1）：15－26.

［11］ 刘宝全，季建华，张 弦.废旧产品再制造环境下的产品定价和再制造方式分配［J］.管理工程学报，2008，22（3）：74－78.

［12］ Giovannia D，Zaccourb G.A two－period game of a closedloop supply chain ［J］.European Journal of Operational Research，2014，232（10）：2－40.

［13］ Xiong Yu，Zhou Yu.Don’t forget your supplier when remanufacturing［J］.European Journal of Operational Research，2013，230（2）：15－25.

［14］ Chen J，Chang C.Dynamic pricing for new and remanufactured products in a closed－loop supply chain［J］.International Journal of Production Economics，2013，146（1）：153－160.

［15］ Atasu A，Sarvary M.Remanufacturing as a marketing strategy ［J］.Management Science，2008，54 （10）：1731－1746.

［16］ 杨爱峰，王 晓.基于回收价格的再制造系统策略研究［J］.合 肥 工 业 大 学 学 报：自 然 科 学 版，2011，34（4）：593－597，608.