大跨径悬索桥缆索承重构件公路火灾的瞬态空间温度场数值模拟
李利军, 万祥斌, 董晓明
(1.山东建筑大学 交通工程学院,山东 济南 250101;2.聊城市公路管理局,山东聊城 252000;3.鲁东大学土木工程学院,山东 烟台
264025)
在世界各国的交通运输中,公路运输具有相当重要的地位。桥梁是公路的枢纽工程,在公路交通中起着至关重要的作用,悬索桥是长大跨径和超长大跨径桥梁最具竞争力的桥型。悬索桥火灾为偶然灾害,在结构设计中并未予以考虑;然而从风险率的角度看,偶然灾害的发生是不可避免的,只是出现概率的多少问题。悬索桥主缆、吊索是主要承重构件,多采用平行钢束、钢丝绳或钢绞线作为承重材料,但钢结构的耐火性能差是一个致命弱点。火灾实验和数值模拟是目前国内外进行火灾研究的主要手段,计算机数值模拟通过设定各种火灾场景进行重复模拟和演算,从而大大节省了研究和测试的费用,是火灾研究的重要手段[1]。悬索桥的主缆是不可更换构件的,一旦其受火损将对整个结构的安全性带来致命的危害,因此开展悬索桥缆索承重构件公路火灾瞬态空间温度场的研究极其必要。
1 公路火灾热释放速率模型
依据Ingason H 的火灾热释放理论[2-5],采用平方增长模型,公路车辆火灾热释放速率模型为:
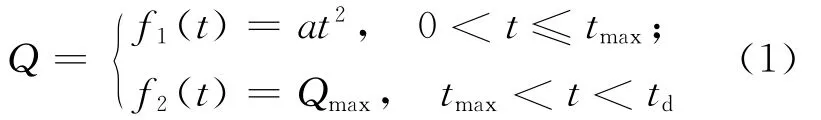
其中,tmax为火灾达到最大热释放率的时间;td为维持最大热释放率的时间;Qmax为火灾最大热释放率。(1)式中各参数的取值见表1所列。
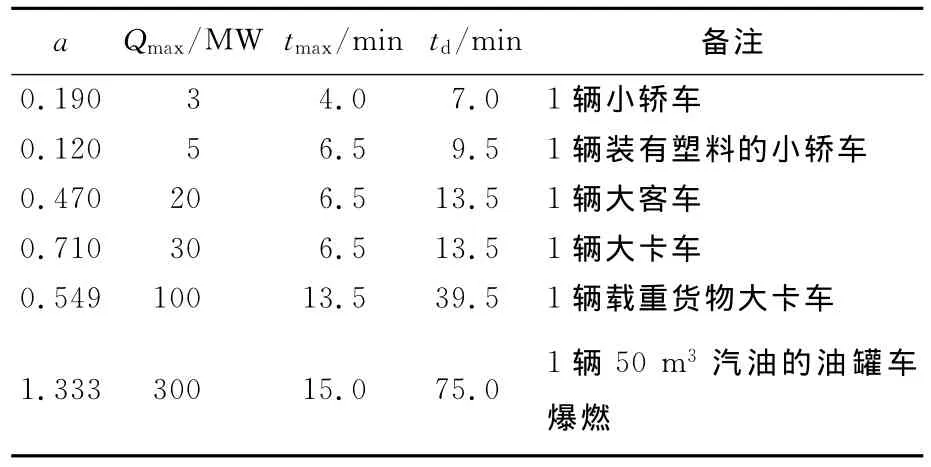
表1 公路火灾参数取值
2 公路火灾物理模型的建立
2.1 模型假定
火灾的发展是一个非常复杂的物理、化学过程,包括多种可燃物的燃烧气体的复杂流动以及传质传热过程[6]。为数值模拟方便,对研究对象做以下假设:① 不考虑具体燃烧过程,将燃烧火源简化为一个固定面积的热源;② 仅模拟1辆车的燃烧;③ 火灾发生前,周围风流、温度均匀;④ 风流及火灾产生的烟气视为理想气体;⑤ 火灾燃烧时产生的烟气在流动过程中不发生化学反应。
2.2 边界条件
公路火灾模拟是开放环境下的火灾动态发展过程,空气的比热容和导热系数不考虑随温度的变化而变化,取为常数,空气温度为22℃。常温下空气密度ρ=1.22kg/m3,重力加速度g=9.8m/s2,外界空气(绝对)压力p=1.013×105Pa;空气的导热系数λ=0.024 2W/(m·℃),空气的比热容c=1 006.43J/(kg·℃);钢 材 导 热 系 数λ=45W/(m·℃);钢材比热容c=600J/(kg·℃);钢材密度ρ=7 850kg/m3。
2.3 模型坐标及热源
模型坐标如图1所示,其中,X方向为车辆纵向,Y方向为车辆横向,Z轴垂直于热源平面,坐标的原点位于热源平面的形心。A、B为热源的长度和宽度。公路火灾稳定燃烧热源见表2所列。
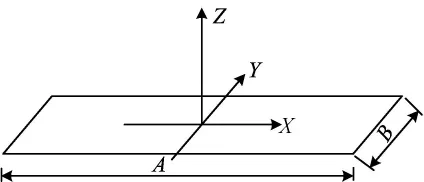
图1 火灾模型坐标

表2 公路火灾热源
公路车辆火灾数值模拟采用的释热率时程曲线如图2所示。
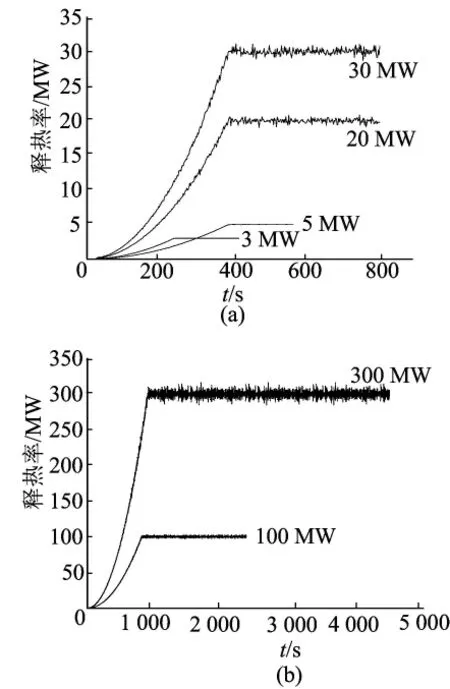
图2 车辆火灾释热率时程曲线
2.4 火灾模型
火灾模型有区域模型和场模型2种,探求火灾的规律应采用场模型[7]。用于模拟开放空间的车辆 火 灾 的 软 件 有 ALOFT-FT、FDS、CFX、FLUENT、PHOENICS、JASMINE。本文采用火灾动力学模拟工具(fire dynamics simulator,FDS),能够描述多种类型的火灾现象[8],由美国国家技术标准局建筑火灾实验室开发,采用场模拟中先进的大涡模拟技术,其准确性得到了大量试验的验证[9],在火灾安全工程领域、火灾科学领域得到了广泛应用[10-11]。
3 悬索桥吊索瞬态空间温度场数值模拟
公路火灾为开放大空间火灾,火焰有一定的几何尺寸,属有限面产生的辐射,与接受辐射面与火焰面之间的相对空间位置有关,火焰的辐射影响有一定的空间范围,在该空间范围以外,可近似不考虑辐射的影响[12]。
3.1 模型建立
用不同断面尺寸的钢柱来模拟吊索,通过调整钢柱与火焰面的X、Y方向的距离来模拟温度效应的空间范围。模拟300MW车辆火灾距离火焰中心面2m处吊索温度效应的模型如图3所示,因为模型温度效应关于X=0的平面对称,因此仅建立X≥0处吊索模型。

图3 300MW车辆火灾吊索温度场模型
3.2 钢柱截面尺寸对表面温度及热流密度的影响
以300MW火源释热率(50m3汽油的油罐车爆燃)为例,分析其对Y=2m平面上钢柱1~5表面(0,2,2)处的温度及热流密度的影响,如图4所示,钢柱1~5的尺寸分别为0.04m×0.04m、0.05m×0.05m、0.06m×0.06m、0.1m×0.1m和0.2m×0.2m。
从图4可见,钢柱1~3的温度和热流密度变化过程基本一致,且温度及热流密度变化相差不大,可忽略差别的影响;随着构件尺寸的增大,温度和热流密度的变化趋势差别较大,且温度和热流密度在同一时间各构件差别较大。
悬索桥吊索钢束的通用直径为0.04~0.06m,通过钢柱1~3瞬态温度场分析,吊索表面温度及热流密度可采用统一的形式。因此本文采用直径为0.05m的钢柱模拟悬索桥吊索的瞬态空间温度场。

图4 300MW车辆火灾柱表面温度和热流密度
3.3 公路火灾吊索瞬态空间温度场
在火灾的初期发展阶段,吊索表面温度的变化比较缓慢,不会对钢材的特性产生影响,在火灾的发展阶段,t时刻的温度为:
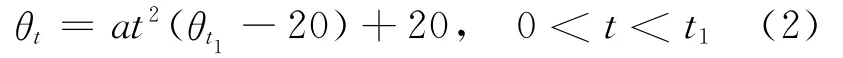
当释热率稳定[13]时,t时刻的温度为:
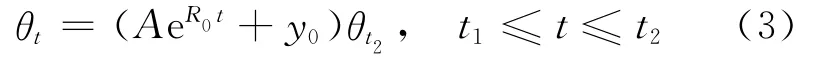
在火灾的发展阶段,钢柱表面热流密度为:

当释热率稳定[13]时,钢柱表面热流密度为:

其中,θt、θt1、θt2分别为构件表面(x,y,z)处在t、t1和t2时刻的温度;HFt、HFt1、HFt2分别为钢柱表面(x,y,z)处在t、t1和t2时的热流密度。各参数的具体取值见表3所列。

表3 直径5cm吊索温度函数和热流密度函数参数
4 悬索桥主缆瞬态空间温度场数值模拟
悬索桥主缆直径变化范围比较大,一般为0.4~1.0m,因此以直径为0.4、1.0m2种索径进行数值分析,各火灾场景下的表面温度及热流密度变化过程如图5所示。

图5 300MW车辆火灾主缆表面温度和热流密度
图5中,对于直径为0.4~1.0m的主缆,采用内插方式计算表面温度及热流密度;(0,2,2)-0.4表示主缆直径为0.4m位于(0,2,2)坐标处;(0,2,4)-1.0表示主缆直径为1.0m 位于(0,2,4)坐标处;(3,2,14)-0.4表示主缆直径为0.4m位于(3,2,14)坐标处;(2,2,16)-1.0表示主缆直径为1.0m 位于(2,2,16)坐标处。
从图5可见,以300MW车辆火灾作用下,0.4m索径的主缆表面的温度θ4500在坐标(0,2,2)和(3,2,14)处的值为936 ℃和505℃,HF4500为130kW/m2和89.9kW/m2;1.0m主缆表面的温度θ4500在坐标(0,2,4)和(2,2,16)处的值为939 ℃ 和 500 ℃,HF4500为 125kW/m2和66.7kW/m2;不同直径主缆不同位置具有相同的θ4500时,温度和热流密度变化趋势基本一致,因此可以采用相同的温度及热流密度变化公式。在火灾的发展阶段,主缆表面温度为:

当释热率稳定时,主缆表面温度为:
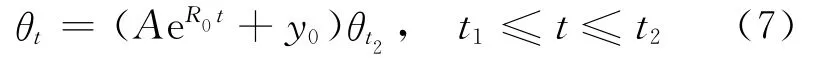
在火灾的发展阶段,主缆表面热流密度为:
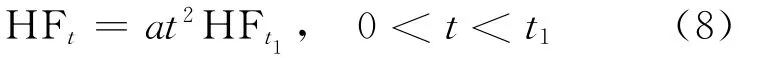
当释热率稳定[13]时,热流密度为:

其中,θt、θt1、θt2分别为构件表面(x,y,z)处在t、t1和t2时刻的温度[13];HFt、HFt1、HFt2分别为构件表面(x,y,z)处在t、t1和t2时刻的热流密度[13]。各参数具体数值见表4所列。

表4 主缆温度函数和热流密度函数参数
5 结束语
本文建立了公路车辆火灾场景对应的6种热释放率数学模型和悬索桥吊索、主缆瞬态空间温度场。通过数值模拟提出吊索表面温度及热流密度随火灾的发展过程而变化的规律公式,从而得出吊索表面瞬态空间的温度场。悬索桥吊索钢束的通用直径为0.04~0.06m,因此吊索瞬态空间温度场具有通用性。
通过数值模拟分别得到直径为0.4、1.0m的悬索桥主缆表面温度及热流密度随火灾的发展过程而变化的规律公式,可采用内插的方式计算其表面瞬态温度及热流密度,从而建立起不同直径悬索桥主缆瞬态空间温度场。
同一火灾场景下,不同直径的吊索可以采用相同的瞬态空间温度场;不同直径的悬索桥主缆不同位置具有相同的θt2时,可以采用相同的瞬态空间温度场。
[1] 丛北华,廖光煌,韦亚星.计算机模拟在火灾科学与工程研究中的应用[J].防灾减灾工程学报,2003,23(2):63-69.
[2] Ingason H.Fire growth rate is more important than maximum heat release rate in tunnel fires[C]//Tunnel Management International.M¨alardalens H¨ogskola,Akademin f¨or Hallbar Samh¨ollsoch Teknikutveckling,2006:669-673.
[3] Ingason H,Bergqvist A,L¨onnermark A,et al.R¨addningsinsatser i v¨agtunnlar R¨addningsverket[R].S¨oren Lundstrom,2005.
[4] Ingason H.Design fires in tunnels[C]//Safe & Reliable Tunnels,Innovative European Achievements,Second International Symposium,Lausanne,2006:1-11.
[5] 杨 涛.公路隧道火灾热释放率及通风方式研究[D].西安:长安大学,2009.
[6] 范维澄,王清安,姜冯辉,等.火灾学简明教程[M].合肥:中国科学技术大学出版社,1995:37-110.
[7] 杨君涛.油罐火灾的数值模拟与实验研究[D].天津:天津大学,2005.
[8] Mc Grattan K B,Forney G P,Floyd J E,et al.Fire dynamics simulator:user's guide,version 3,NIST IR6784[R].Gaithersburg,MD:National Institute of Standards and Technology,2001.
[9] Floyd J E,Mc Grattan K B,Hostikka S,et al.CFD fire simulation using mixture fraction combustion and finite volume radiative heat transfer[J].Journal of Fire Protection Engineering,2003(13):11-36.
[10] Madrzykowski D,Vettori R L.Simulation of the dynamics of the fire at 3146Cherry Road NE,Washington D C,May 30,1999,Technical Report NISTIR 6510[R].Gaithersburg,MD:National Institute of Standards and Technology,2000.
[11] 薛 伟,张光俊.贮木场楞堆火灾场景模拟设计[J].林业机械与木工设备,2006(8):33-35.
[12] 何 翔,方诗圣,方 飞,等.不同梯度温度作用下曲线桥梁的温度效应分析[J].合肥工业大学学报:自然科学版,2012,35(8):1088-1092.
[13] 李利军.公路火灾温度场数值模拟及大跨径缆索承重桥梁火灾分析[D].西安:长安大学,2013.

