采用NSGA-II算法的混合动力能量管理控制多目标优化方法

邓涛,林椿松,李亚南,卢任之

(重庆交通大学机电与车辆工程学院, 400074, 重庆)



采用NSGA-II算法的混合动力能量管理控制多目标优化方法

邓涛,林椿松,李亚南,卢任之

(重庆交通大学机电与车辆工程学院, 400074, 重庆)

综合考虑燃油经济性、排放性与驾驶性对混合动力能量管理控制优化的优点,以某款并联混合动力汽车为研究对象,选取能量管理控制参数与传动系参数作为待优化参数,以动力性作为约束条件,建立混合动力能量管理控制多目标优化评价方法,提出基于NSGA-II算法的混合动力系统多目标优化方法,并与优化前控制策略进行仿真对比分析。结果表明:在满足基本约束的前提下,优化后燃油经济性最多提高了7.8%,平均提高了6.38%;驾驶性性能指标最多提高了27.12%,平均提高了21.74%;排放性综合指标平均提高了41.51%。提出的多目标优化算法具有良好的收敛性与分布性,得到的Pareto最优解集能够给混合动力能量管理控制策略提供更多的权衡选择方案,体现了多目标优化的优势。

混合动力;能量管理;Pareto最优解;NSGA-II算法;多目标优化

在已有混合动力(HEV)能量管理控制策略的研究中,大部分都侧重于提高燃油经济性,对排放性和驾驶性关注甚少。如基于电池组荷电状态(SOC)的闭环控制策略[1]、等效燃油消耗(equivalent consumption minimization strategies,ECMS)[2]控制策略、基于近似极小值原理的实时控制策略[3]等都是以混合动力系统瞬时效率最高为控制目的,其主要优化对象为发动机,然而提高发动机瞬时效率并不能保证整车性能最优。动态规划(dynamic programming,DP)[4]、随机动态规划(stochastic dynamic programming,SDP)[5]等是根据对工况信息的获知,以优化整个行驶路径系统效率最优为控制目的,理论上可以达到瞬时或全局最优,但计算量大,不适合实时控制。也有学者综合考虑了燃油经济性与排放性两目标在优化上存在互斥关系,提出了两目标优化能量管理控制策略[6-9],并通过加权系数法处理多目标优化问题,其本质仍然是单目标优化,且没有考虑驾驶性的影响[10]。然而,驾驶性涵盖很多方面,如振动、加减速、制动、换挡等,对混合动力能量管理控制会造成较大影响[11-13]。国外有少数研究人员在能量管理控制中考虑了驾驶性,将发动机起动阶段驾驶性能作为次优参数,嵌入到发动机起动过程惩罚函数中,采用ECMS算法解决其离线优化控制问题[14],但该方法依然属于单目标优化。此类方法处理多目标问题,存在无法消除目标间的相互影响、不能反映优化目标的真实情况、加权系数难以合理选择等缺陷[15]。因此,本文提出综合考虑燃油经济性、排放性与驾驶性的NSGA-II多目标优化算法,实现客观评价各个目标性能,弥补已有混合动力多目标研究的不足。

1 混合动力能量管理控制对象

1.1 研究对象

本文以某款并联混合动力为研究对象,整车布局如图1所示,整车参数如表1所示。发动机与离合器直接连接,通过转矩耦合与电机输出功率进行耦合,经CVT、主减速器传输给车轮,通过控制离合器与电机可实现纯电动模式、发动机单独驱动模式、混合驱动模式、轻载充电模式与能量回馈模式。

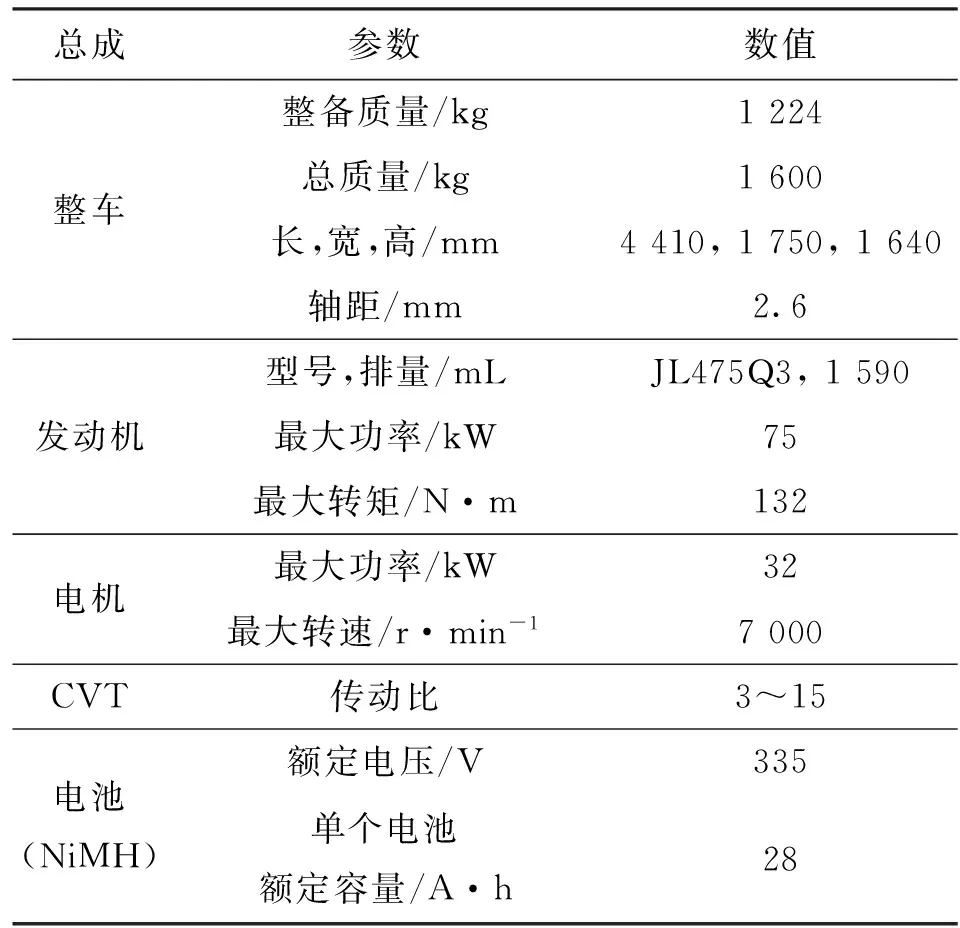
总成参数数值整车整备质量/kg1224总质量/kg1600长,宽,高/mm4410,1750,1640轴距/mm2.6发动机型号,排量/mLJL475Q3,1590最大功率/kW75最大转矩/N·m132电机最大功率/kW32最大转速/r·min-17000CVT传动比3～15电池(NiMH)额定电压/V335单个电池额定容量/A·h28

1.2 优化参数及约束条件

影响燃油经济性、排放性与驾驶性的参数很多,若全部优化,会导致优化过程复杂且难以实现。因此,根据实验与经验选取对优化目标及整车性能影响较大的控制策略和传动系统参数作为优化参数,实现整车性能优化。当然,传动系参数在前期优化设计中可以改变,实车则不能更改,但控制策略参数可改变。具体参数如表2所示。

约束条件主要包括基本动力性和电池荷电平衡约束。加速性与爬坡性是动力性评价的基本指标。由于电池在行驶中提供能量,故不能直接用发动机评判燃油经济性。本文对电池荷电状态进行校正,保证在循环工况前后荷电状态差值在0.5%以内,实现经济性客观评价。优化前与优化后整车都应满足的条件如表3所示。

表2 优化参数

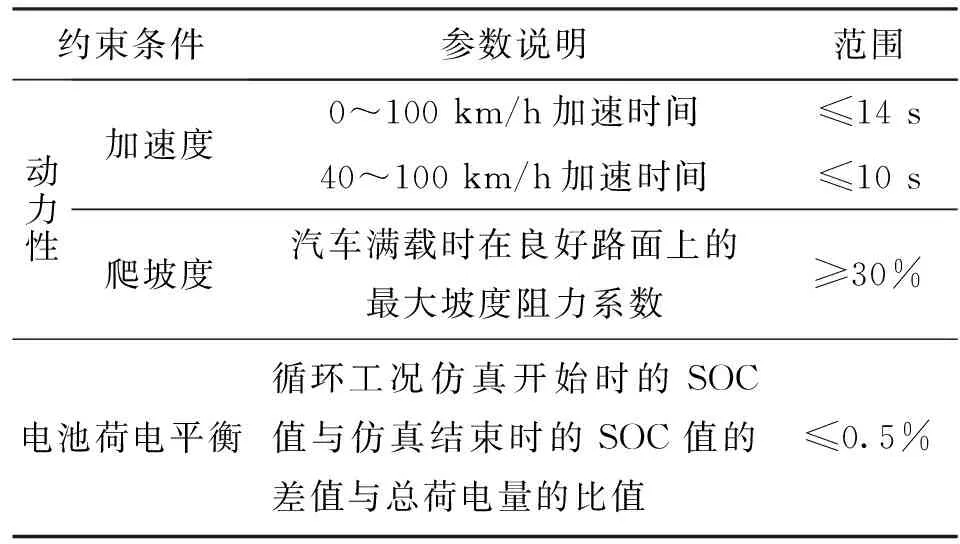
表3 约束条件

2 基于Pareto解集的混合动力多目标优化算法

2.1 多目标优化问题数学模型

典型的多目标优化问题数学模型由n个决策变量、m个目标变量和若干约束条件组成,表示为

(1)

式中:x为n维决策矢量,组成决策空间;f(x)为m维目标空间,组成目标空间;目标函数F(x)是由m维决策空间到目标空间的映射;约束条件gj与hk分别为j维不等式约束和k维等式约束组成。

多目标优化时各个目标间相互冲突,不存在同时达到最优状态,解集与单目标优化相比,存在多组

非劣解集,用Pareto原理表示,称为Pareto解集。

2.2 混合动力多目标优化数学建模

根据多目标问题数学模型建立燃油经济性、排放性与驾驶性混合动力多目标优化数学模型。

2.2.1 燃油经济性 以发动机最终消耗的燃油量为燃油经济性能评价指标,并进行SOC校正,保证电池使用前后的荷电平衡,则燃油经济性评价指标数学模型为

f1(x)=Qfc(x)

(2)

式中:f1(x)为燃油经济性评价指标;Qfc(x)为燃油消耗量。

以发动机数学模型为基础,根据稳态工况下的发动机特性实验数据建立发动机燃油消耗模型为

(3)

式中:Pe为发动机功率;be为燃油消耗率;we为发动机转速;Te为发动机扭矩。

2.2.2 排放性 以CO、NOx、HC排放量为排放性评价指标,为降低目标函数维数,将排放性3个指标合并成1个排放性综合评价函数(直接求和),最终建立排放物评价数学模型为

(4)

排放模型为

(5)

(6)

(7)

式中:f2为排放性综合评价指标;QCO、QHC、QNOx分别为CO、HC、NOx的排放量;ECO、EHC、ENOx分别为CO、HC、NOx的排放率。

2.2.3 驾驶性 以驾驶性的客观评价指标为研究对象,为简化驾驶性评价的复杂度,本文仅以冲击度为例表征整车驾驶性能,将冲击度绝对值的积分作为驾驶性评价指标,则驾驶性评价模型为

(8)

冲击度为车速二阶导数,表达式为

j=d2v/dt2

(9)

式中:f3为驾驶性评价指标;j为整车冲击度;v为车速。

综上所述,以燃油经济性、排放性与驾驶性为优化目标的并联混合动力多目标优化数学模型为

(10)

式中:y为权衡Pareto解集(通过非支配排序与拥挤距离的方法);gj为动力性与荷电平衡约束条件。

2.3 混合动力多目标优化仿真模型

结合上述数学公式和已有的实验数据,以燃油经济性、排放性与驾驶性为研究目标,采取后向为主,前向为辅的方式,建立混合动力汽车多目标优化仿真模型,如图2所示。连线的方向表示能量的流向,其中整车控制策略模块中包括发动机控制模块、电机控制模块、离合器控制模块、电机控制模块、驱动力制动力控制模块,通过底层数据传输的方式控制各个部件。

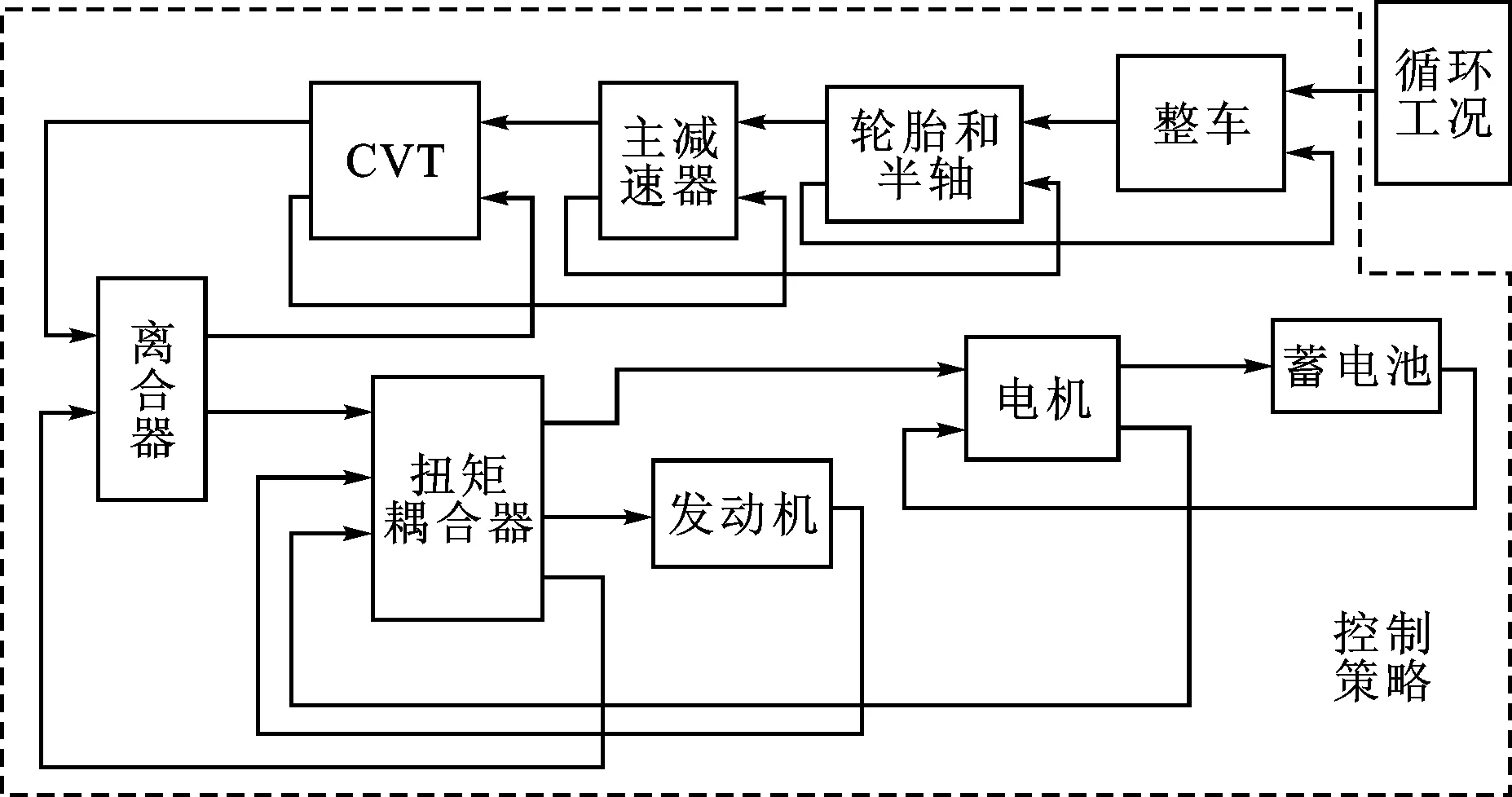
图2 整车建模的顶层方框图

3 基于改进NSGA-II算法的混合动力能量管理多目标优化算法

3.1 改进NSGA-II多目标优化算法

考虑目前能量管理多目标研究多采用加权等方法存在的缺陷,采用Pareto非支配原理处理各个目标间的相互关系,无需加权等数学处理,得到真实的权衡Pareto解集,并以非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm-II,NSGA-II)为实现基础,结合文中问题特点进行改进,提出混合动力系统NSGA-II多目标优化算法。

根据混合动力待优化参数的特点,使用实数编码,进行模拟二进制交叉变异,针对仿真模型运行速度慢以及优化参数特点各异致使算法收敛速度慢、仿真时间长的缺点,对算法交叉变异的过程进行改进,模拟二进制交叉变异过程为

(11)

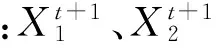
算法前期需要较大的全局搜索能力,以挖掘全局最优解,后期则需要较大的局部搜索能力,以挖掘最优解的分布性,并加快收敛速度,故需要α、θ能根据解集的变化做出相应变化,以最大提高算法性能。本文对算法做进一步改进,使α、θ能跟随解集的变化而自适应的改变,其自适应变化模型表示为

(12)

式中:γ为自适应变异系数;N为种群个数;Np最优解个数;αγ、θγ分别为自适应交叉变异系数。

3.2 混合动力能量管理多目标优化算法实现

通过优化算法与仿真模型联合仿真实现,首先在Simulink中建立多目标优化仿真模型,然后编制NSGA-II多目标优化算法。算法流程如图3所示。

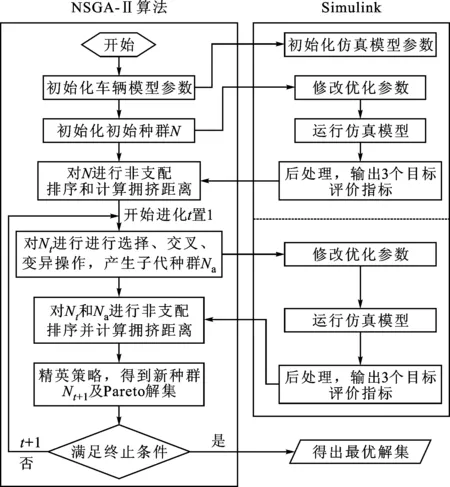
图3 NSGA-II优化算法流程

具体如下:①初始化车辆模型,调入仿真所需要的参数,同时初始化进化过程的参数,并按算法要求初始化种群P;②将初始化种群N中的个体依次赋值给Simulink仿真模型,修改控制策略、传动系的待优化参数,运行仿真模型,并校正SOC平衡,仿真结束,输出性能指标,并判断是否满足约束条件,以惩罚系数处理不满足约束条件的个体,使其在进化中被淘汰,最后输出燃油经济性、排放性与驾驶性3个目标评价指标;③以此方法对种群中所有个体均进行同样操作,得到相应的目标评价指标,完成初始种群初始化操作;④对初始种群进行非支配排序并计算拥挤距离,得出个体的优劣性评价指标;⑤开始进化,以t记录进化次数,初始为1,根据个体的优劣性指标选取父代种群Nt,按上文给定的算法产生子代种群Nct;⑥联合Simulink仿真每个子代种群的性能指标,得到相应的目标值;⑦将子代种群与父代种群合并在一起,进行非支配排序并计算拥挤距离,得出中间种群的优劣性指标;⑧更新种群,对父代子代合并的种群进行修剪,得到更新后的种群Nt+1;⑨判断是否满足终止条件,是则输出最优Pareto解集,否则继续迭代寻优。

4 NSGA-II多目标优化仿真分析

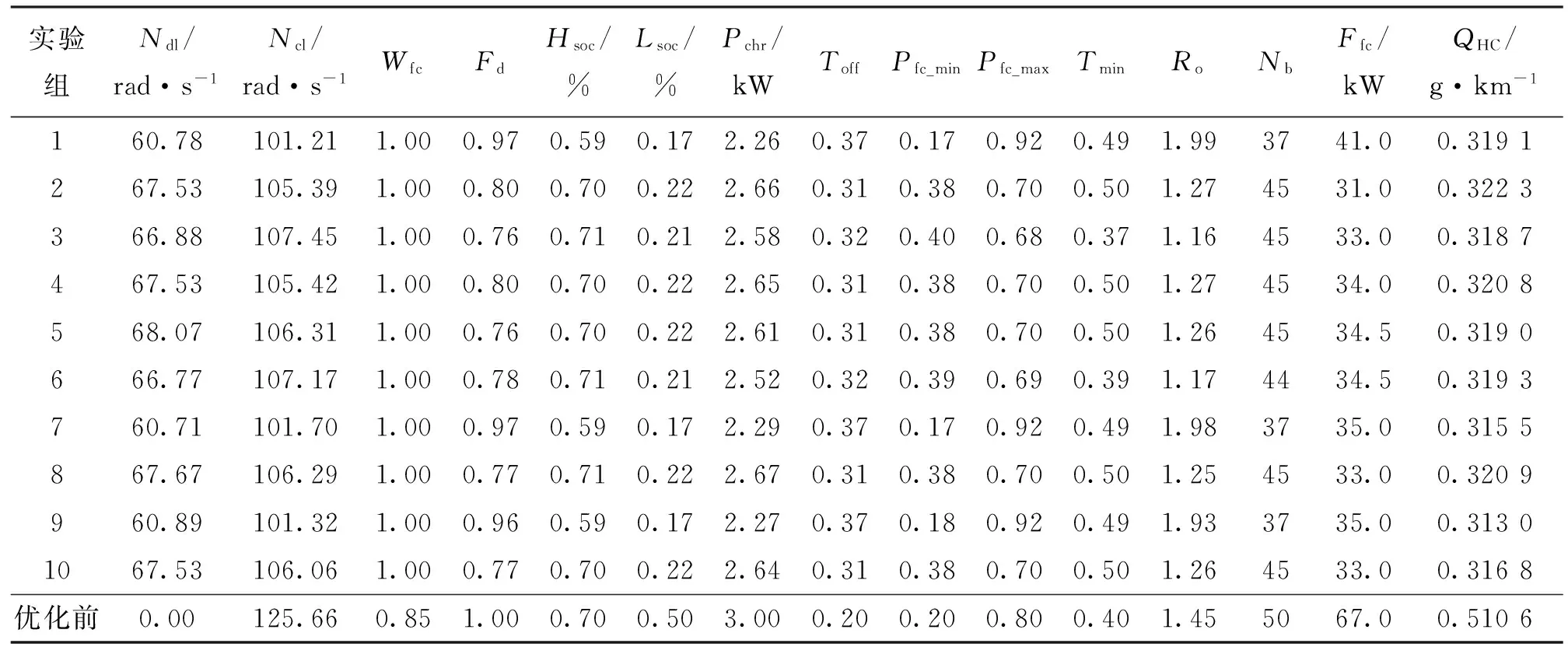
在UDDS市区循环工况下对NSGA-II算法进行多次仿真,选取10组Pareto最优解集如表4所示,最后一组为优化前设置及其性能指标。对比优化前后可知,解集均能收敛到Pareto最优解集,均得到优化。以表4中第3组解集为例,对最优解对应的性能进一步分析,得到的最优解对应的SOC值(SSOC)变化情况如图4所示,UDDS工况下车速跟随及误差如图5所示,发动机工作效率点分布如图6所示。可以看出,本文方法获取的Pareto解集不仅满足约束条件,而且最优解对应的SOC变化合理,车速跟随良好,发动机工作效率提高。

由图4可见,电机单独驱动时,

SSOC下降, 随后

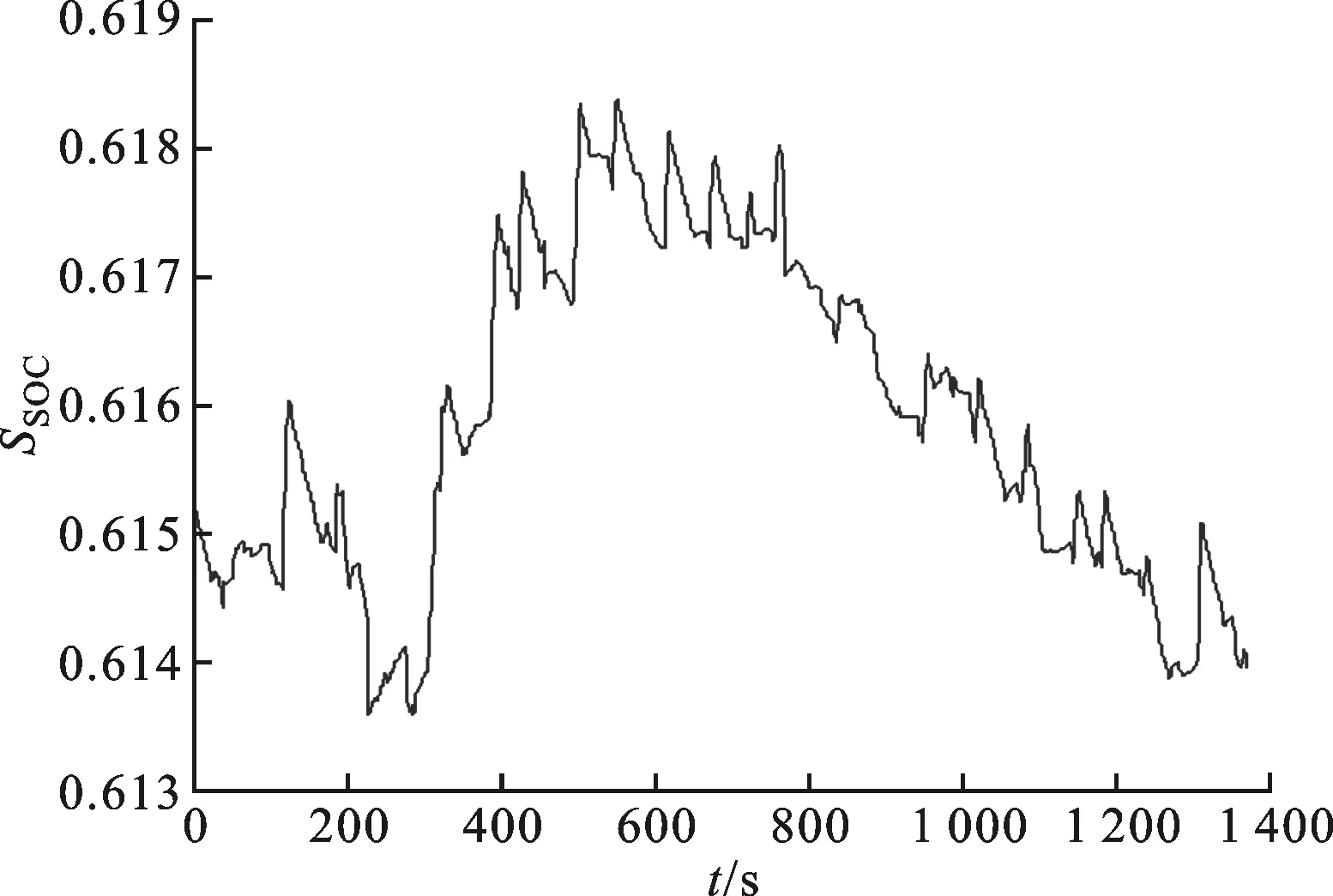
图4 Pareto最优解对应的SOC变化情况

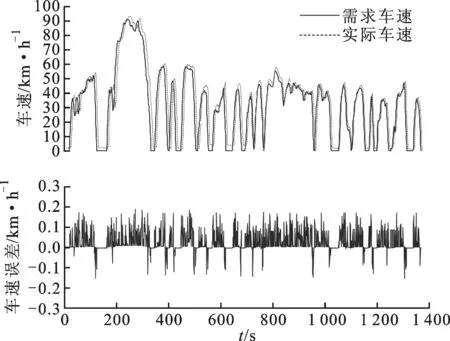
图5 UDDS工况下的车速跟随及误差

车速有所下降,回收制动能量,SSOC上升,在165s到250s车速上升,SSOC迅速下降,小段波动后在259s到334s车速急剧下降,制动回收能量,SSOC急剧上升,之后在383到397,车速下降,SSOC急剧上升。此后随着车速变化,SSOC变化较小,充放电比较平缓。整个工况中SSOC上升主要来源于制动能量的回收,仿真始末SSOC误差较小, 小于0.5%, 且整个过程SSOC波动较小,变化合理,满足设定的要求。由图5可以看出,

UDDS工况下车速跟随能力良好, 误差

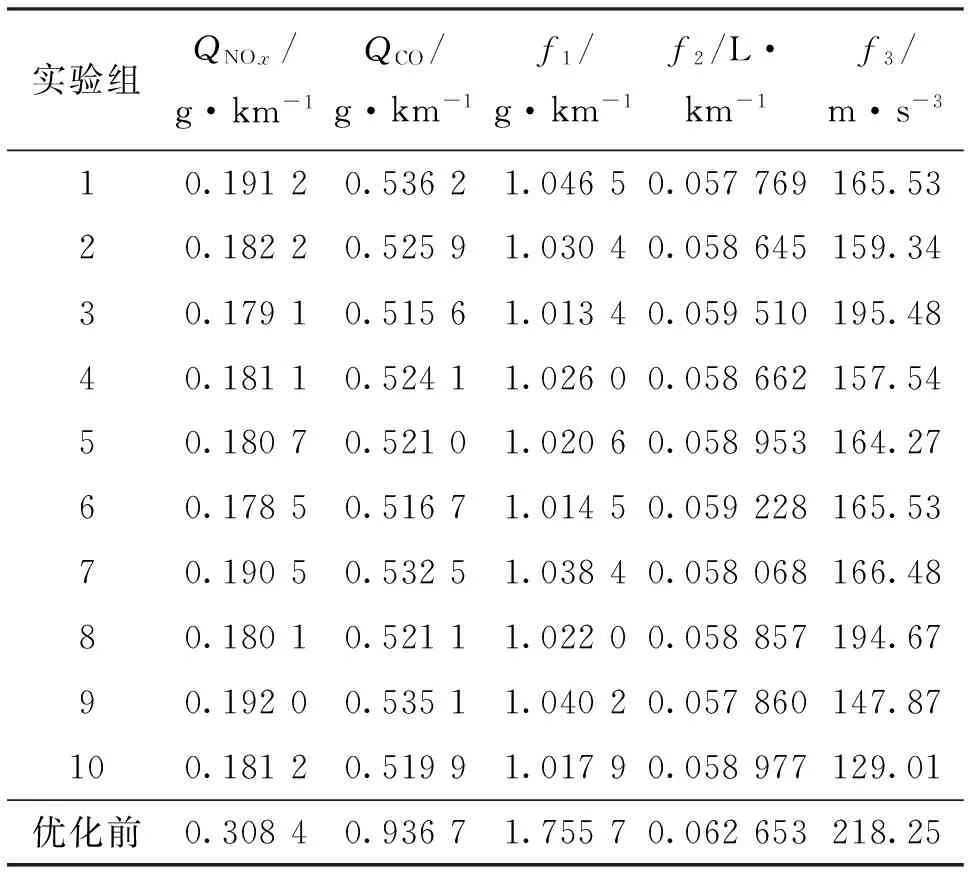
续表4

小,满足要求。

由表4可知,相比于优化前,10组Pareto最优解集的参数得到了优化,其中对于燃油经济性,最大提高了7.8%,所选数据中平均优化指标提高了6.38%;对于驾驶性,最大优化性能能够达到27.12%,平均性能也能达到21.74%;排放性综合指标平均提高了41.51%,其中QHC、QNOx、QCO分别提升了37.61%、40.45%、43.97%。具体如表5所示。

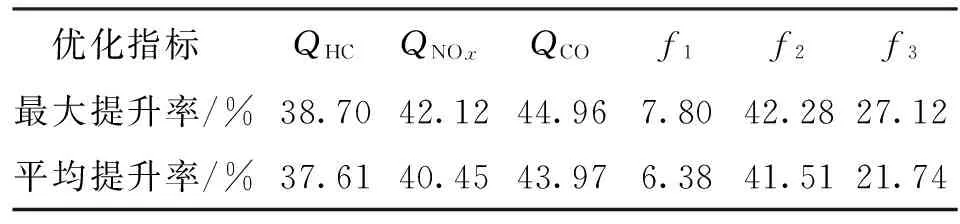
表5 优化指标提升率

由于CVT以燃油经济性为目标实现发动机在经济区工作,故优化前发动机工作点在经济区分布较多,优化后燃油经济性提高不大。

图6为发动机工作效率点分布情况。可以看出:优化后工作在33%效率区域内的工作点发生变化,并有所减少,但是整体分布于高效区域的点有所增多,并考虑需求功率,更多点工作于经济区域,所以燃油经济性有所提高;优化前后,发动机的工作点分布情况发生了很大变化,因为优化前的控制策略仅考虑燃油经济性这一目标进行控制,单纯从降低燃油消耗量实现降低排放,但是发动机的燃油消耗经济区域与排放物的经济区域并不一致,具有明显的冲突关系,并且驾驶性与这2个目标也有冲突关系,因此综合考虑燃油经济性、排放性与驾驶性进行优化的发动机工作点有很大变化,使排放性与驾驶性得到了很大的提高,得到更为均衡分布的工作点。

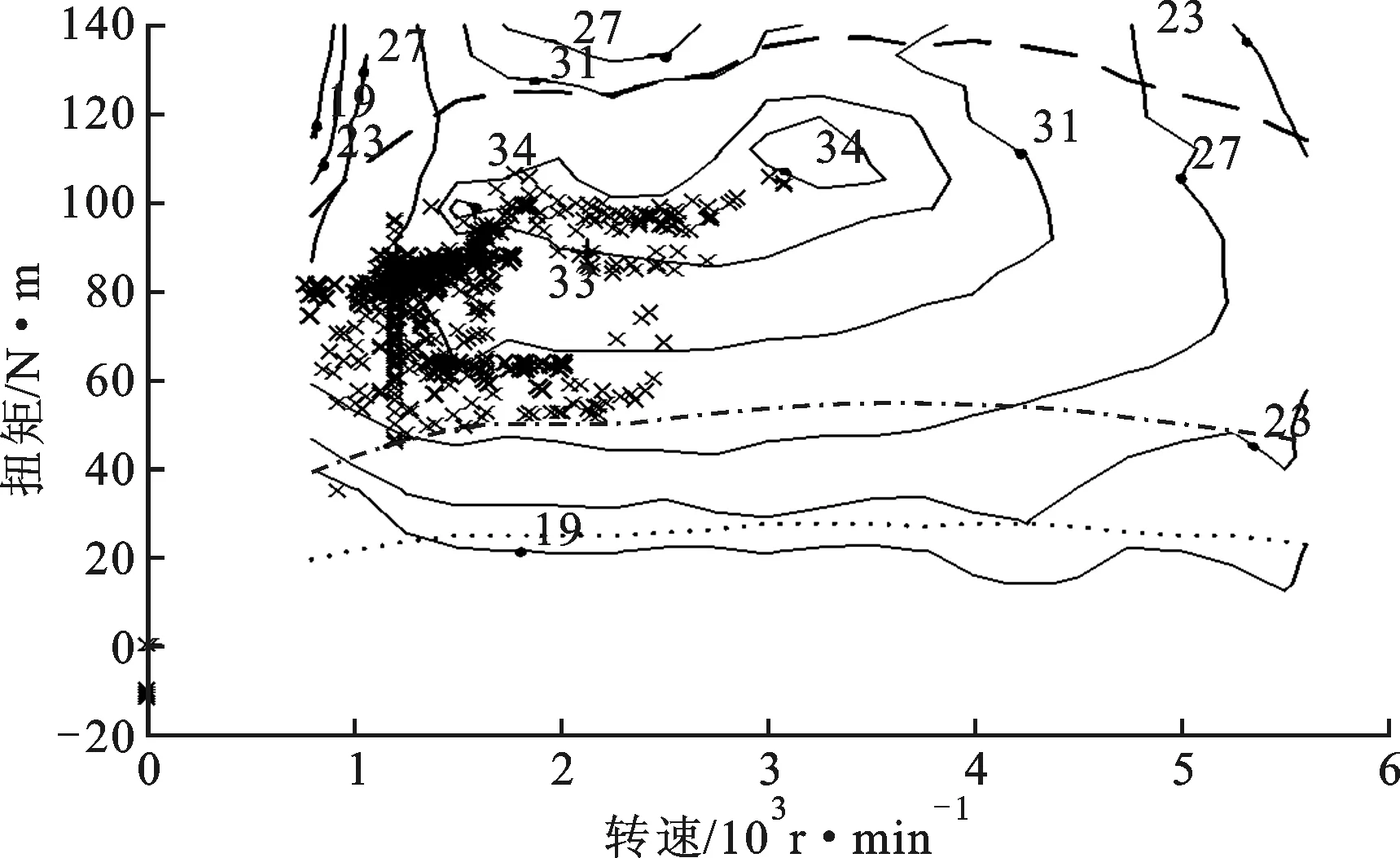
(a)优化前发动机工作效率点分布

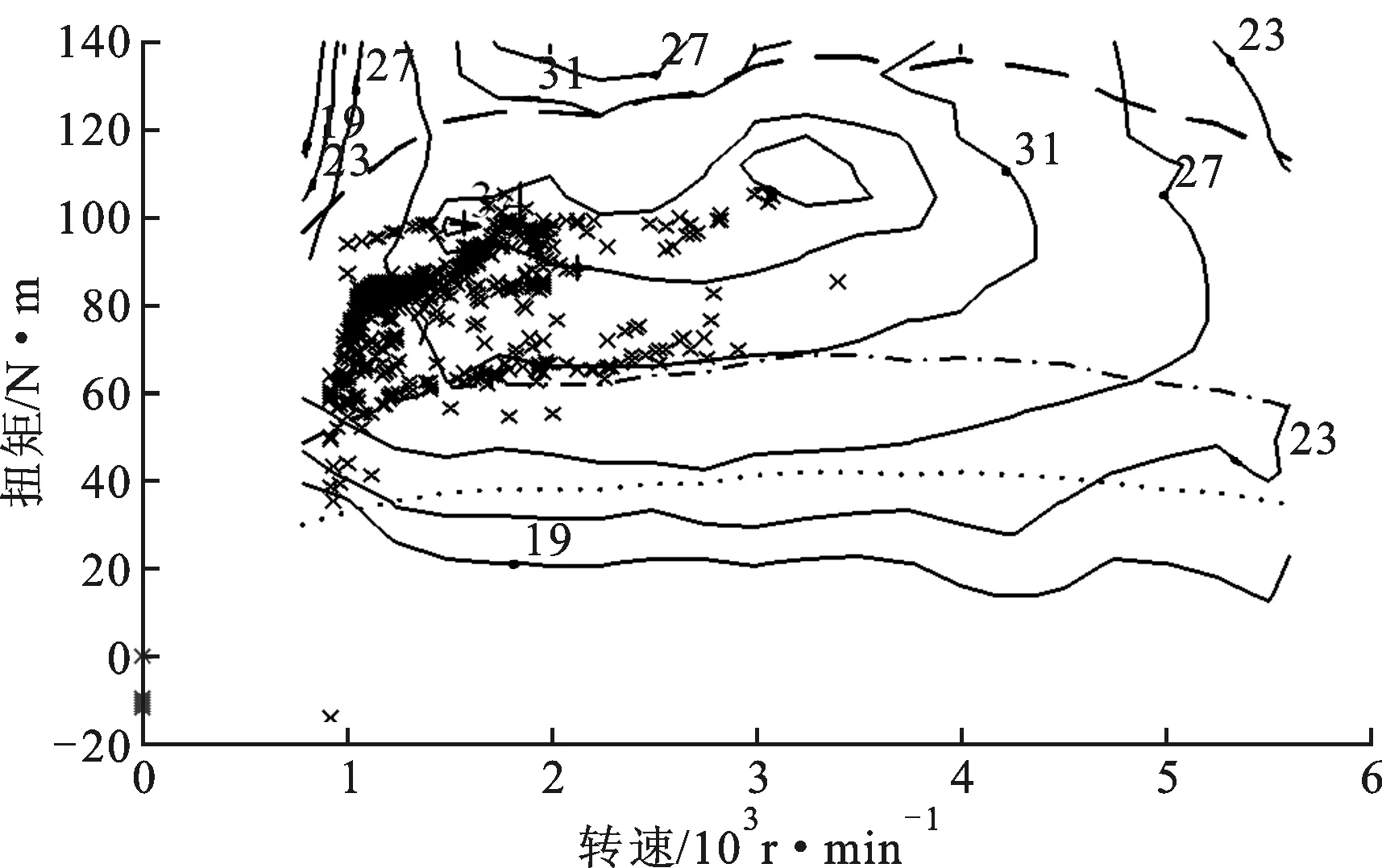
(b)优化后发动机工作效率点分布- - -最大转矩;……CS最小转矩;——燃油效率(%);-·-·-CS关闭转矩;×发动机工作点图6 发动机工作效率点分布情况

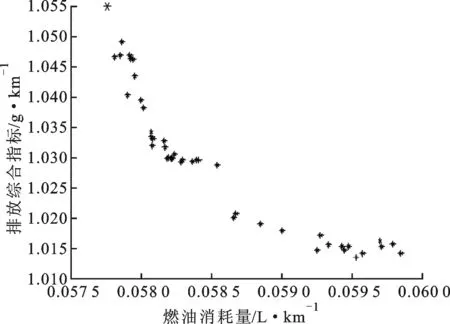
图7 燃油消耗量与排放综合指标权衡控制

图7为燃油消耗量与排放综合指标权衔控制图。可以看出,最优Pareto解集相比于优化前均得优化(优化前燃油消耗量为0.062 7 L/km,排放性指标为1.755 7 g/km),由于前文论述两目标的冲突性,其解集分布如图所示,满足多目标Pareto解集的理论要求;同时清晰地反应了燃油经济性、排放性与驾驶性之间的关系,将Pareto最优解作图分析,如图8所示。

图8为优化前与优化后燃油经济性、排放性综合指标及驾驶性指标Pareto最优解集的分布图。由图8可见,燃油经济性、排放性与驾驶性3个目标表现出相互冲突的关系,可以获得多组多目标优化方案。设计者可根据设计需要或性能侧重程度,选取恰当的Pareto集,这也是多目标优化的意义所在。

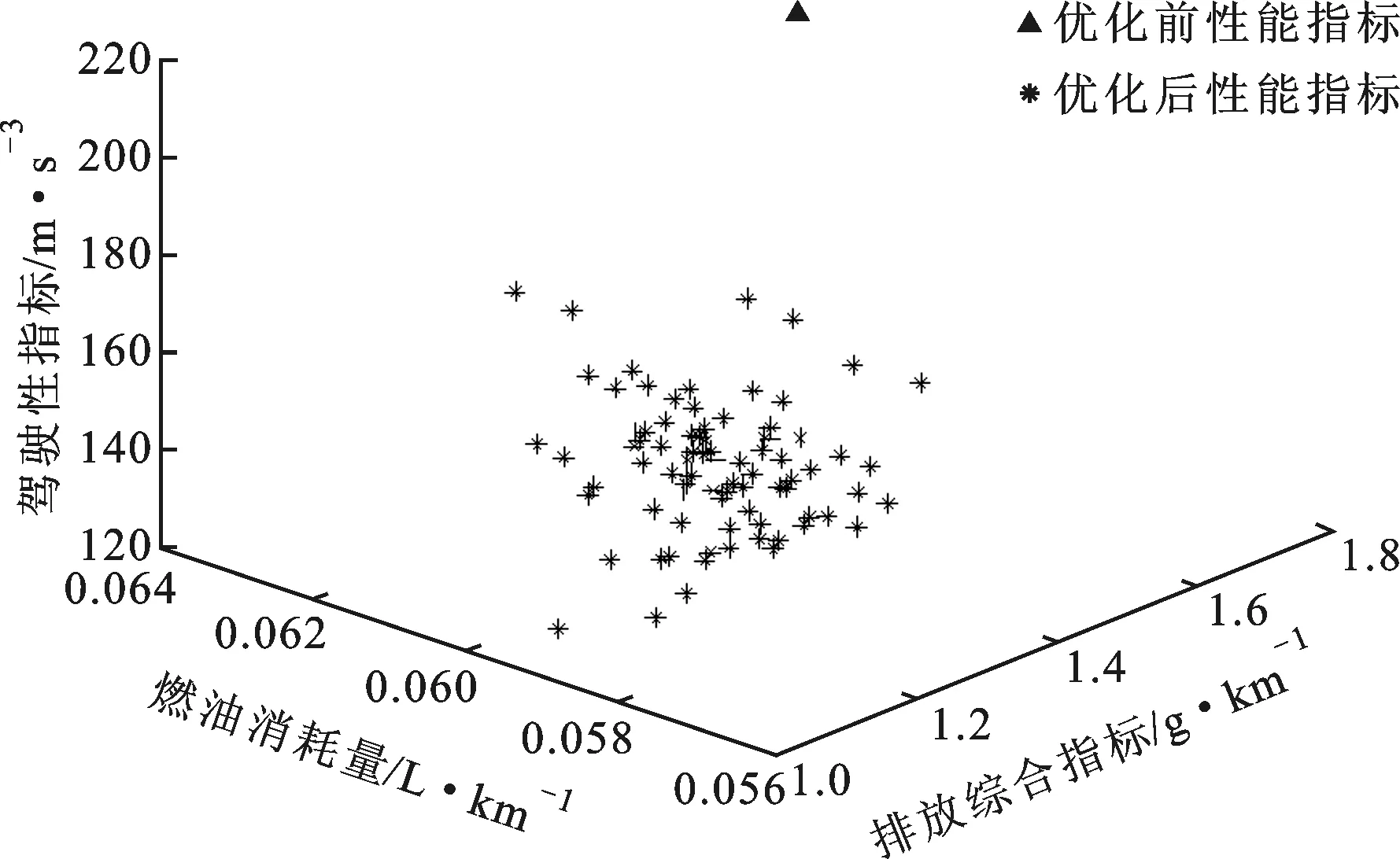
图8 Pareto最优解集分布图

5 结 论

(1)已有的混合动力能量管理控制系统优化研究集中在燃油经济性优化,对排放性、驾驶性很少关注,本文综合考虑燃油经济性、排放性与驾驶性对能量管理控制的影响,提出了综合考虑3个目标的混合动力多目标优化方法。

(2)针对目前混合动力能量管理系统单目标优化或者加权多目标优化的缺点,提出了NSGA-II算法,仿真结果满足约束条件,并得到真实的权衡Pareto最优解集。

(3)仿真结果表明,在满足基本约束条件下,汽车性能得到优化:燃油经济性评价指标最多提高了7.8%,平均优化指标提高了6.83%;排放性综合评价指标提高了41.51%;驾驶性评价指标最多提高了27.12%,平均性能优化提高了21.74%。得到的权衡Pareto解集具有良好的分布性与收敛性,满足多目标优化的理论。

(4)多目标优化得到的权衡Pareto解集反映出目标解集的真实性、冲突性,为前期设计提供了更多选择方案。需要进一步研究的是构建解集曲面和分析其他驾驶性评价指标对Pareto解集的影响。

[1] 张冰战. 插电式混合动力电池汽车能量管理策略研究 [D]. 合肥: 合肥工业大学, 2011.

[2] 李翔晟, 陈斗, 周永军. 基于最小瞬时等效燃油消耗的液压混合动力车辆能量管理策略 [J]. 公路交通科技, 2012, 29(12): 148-152. LI Xiangsheng, CHEN Dou, ZHOU Yongjun. Energy management strategy of hydraulic hybrid vehicle based on instantaneous equivalent fuel consumption minimization [J]. Journal of Highway and Transportation Research and Development, 2012, 29(12): 148-152.

[3] 秦大同, 曾育平, 苏岭, 等. 基于近似极小值原理的插电式混合动力汽车实时控制策略 [J]. 机械工程学报, 2015, 51(2): 134-140. QIN Datong, ZENG Yuping, SU Ling, et al. Plug-in hybrid vehicle’s real-time control strategy based on approximate Pontryagin’s minimum principle [J]. Journal of Mechanical Engineering, 2015, 51(2): 134-140.

[4] 杨亚联, 蒲斌, 胡晓松, 等. ISG型速度耦合混合动力系统全局最优控制方法 [J]. 重庆大学学报, 2013, 36(9): 71-77. YANG Yalian, PU Bin, HU Xiaosong, et al. Study on global optimization control strategy of ISG velocity coupling hybrid electric vehicle [J]. Journal of Chongqing University, 2013, 36(9): 71-77.

[5] 肖仁鑫, 李涛, 邹敢, 等. 基于随机动态规划的混联式混合动力汽车能量管理策略 [J]. 汽车工程, 2013, 35(4): 317-321. XIAO Renxin, LI Tao, ZOU Gan, et al. Energy management strategy for series-parallel hybrid electric vehicle based on stochastic dynamic programming [J]. Automotive Engineering, 2013, 35(4): 317-321.

[6] PATRICK M W. Plug-in hybrid electric vehicle supervisory control strategy considerations for engine exhaust emissions and fuel use [D]. Blacksbury, VA, USA: Virginia Polytechnic Institute and State University, 2011.

[7] 秦大同, 隗寒冰, 段志辉, 等. 重度混合动力汽车油耗和排放多目标实时最优控制 [J]. 机械工程学报, 2012, 48(6): 83-89. QIN Datong, WEI Hanbing, DUAN Zhihui, et al. Multiple-objective real-time optimum control strategy for fuel consumption and emission of full hybrid electric vehicle [J]. Journal of Mechanical Engineering, 2012, 48(6): 83-89.

[8] PIERRE M, ALAIN C, GUILLAUME C, et al. Energy management of HEV to optimize fuel consumption and pollutant emissions [C]∥Proceedings of 11th International Symposium on Advanced Vehicle Control. Yokohama, Japan: JSAE, 2012: 81-87.

[9] WANG Q, FRANK A A. Plug-in HEV with CVT: configuration, control, and its concurrent multi-objective optimization by evolutionary algorithm [J]. International Journal of Automotive Technology, 2014, 15(1): 103-115.

[10]SHASHI K A, WANG G, AN L Q, et al. Using the Pareto set pursuing multi-objective optimization approach for hybridization of a plug-in hybrid electric vehicle [J]. Journal of Mechanical Design, 2012, 134(9): 503-509.

[11]GALVAGNO E, MORINA D, SORNIOTTI A, et al. Drivability analysis of through-the-road-parallel hybrid vehicles [J]. Mechanical, 2013, 48(2): 351-366.

[12]岳明玥, 周一丹, 马改. 深度混合动力汽车NVH问题的研究进展 [J]. 机械设计与制造, 2015(2): 268-271. YUE Mingyue, ZHOU Yidan, MA Gai. Research progress on deep hybrid vehicle NVH problem [J]. Machinery Design & Manufacture, 2015(2): 268-271.

[13]郑宏宇, 王琳琳, 赵伟强, 等. 基于电控制动系统的客车制动力分配控制策略 [J]. 吉林大学学报: 工学版, 2015, 45(2): 347-351.

ZHENG Hongyu, WANG Linlin, ZHAO Weiqiang, et al. Braking force distribution control strategy of bus based on electronically controlled braking system [J]. Journal of Jilin University: Engineering and Technology Edition, 2015, 45(2): 347-351.

[14]DANIEL F O, WANG X Y, RYAN M, et al. An energy management controller to optimally trade off fuel economy and drivability for hybrid vehicles [J]. IEEE Transactions on Control Systems Technology, 2012, 20(6): 1490-1505.

[15]宋康, 陈潇凯, 林逸. 汽车行驶动力学性能的多目标优化 [J]. 吉林大学学报: 工学版, 2015, 45(2): 352-357. SONG Kang, CHEN Xiaokai, LIN Yi. Multi objective optimization of vehicle dynamic behaviors [J]. Journal of Jilin University: Engineering and Technology Edition, 2015, 45(2): 352-357.

(编辑 刘杨 苗凌)

A Multi-Objective Optimization Method for Energy Management Control of Hybrid Electric Vehicles Using NSGA-II Algorithm

DENG Tao,LIN Chunsong,LI Yanan,LU Renzhi

(School of Mechatronics & Automotive Engineering, Chongqing Jiaotong University, Chongqing 400074, China)

A multi-objective optimization evaluation method for hybrid electric vehicle (HEV) is proposed by comprehensively considering the influences of fuel economy, emission and drivability on the energy management control for HEV. The multi-objective optimization algorithm based on NSGA-II (non-dominated sorting genetic algorithm-II) is established by setting the parameters of the energy management control and the driveline system as the optimal parameters for the parallel hybrid electric vehicles, and the dynamic performance as the constraint condition. Then the proposed method is comparatively analyzed with the traditional control strategy that only considers the fuel economy. Simulation results show that the maximum fuel economy performance increases by 7.8% and the average value increases by 6.38%; the maximum drivability performance increases by 42.28% and the average value increases by 21.74%; the average synthetic emission performance increases by 41.51%. The proposed multi-objective optimization algorithm has good convergence and distribution. The obtained Pareto optimum solutions may provide more trade-off options for HEV energy management control strategy, which reflect the advantages of multi-objective optimization.

hybrid power; energy management; Pareto optimal solution; NSGA-II algorithm; multi-objective optimization

2015-01-28。

邓涛(1982—),男,博士,副教授,硕士生导师。

国家自然科学基金资助项目(51305473);中国博士后科学基金资助项目(2014M552317);重庆市基础与前沿研究计划项目(cstc2013jcyjA0794);重庆市教委科学技术研究资助项目(KJ120421);重庆市博士后研究人员特别资助项目(xm2014032)。

时间:2015-07-23

10.7652/xjtuxb201510023

U469.7;TP18

A

0253-987X(2015)10-0143-08

网络出版地址:http://www.cnki.net/kcms/detail/61.1069.T.20150723.0922.002.html