联合串行干扰抵消与因子图的单通道混合信号盲分离算法

郭一鸣,彭华,张冬玲,杨勇

(解放军信息工程大学信息系统工程学院, 450001, 郑州)



联合串行干扰抵消与因子图的单通道混合信号盲分离算法

郭一鸣,彭华,张冬玲,杨勇

(解放军信息工程大学信息系统工程学院, 450001, 郑州)

为解决复杂编码方式下单通道同频混合信号盲分离复杂度高的问题,提出了一种联合串行干扰抵消(SIC)与因子图的迭代分离算法。首先由传输信道参数来重构发送信道,然后根据重构信道进行SIC解调,获得解调信号软信息传递给译码模块,将译码增益反馈回SIC解调模块,利用迭代处理来实现分离。重点研究了解调与译码间信息迭代交互过程,以及2路信号分量的信道参数差异对分离性能的影响,得到随着迭代次数的增加以及信道参数差异性增加,算法分离性能将得到提升的结论。仿真实验表明,在LDPC编译码环境下,QPSK调制混合信号经2次迭代处理,分离性能较M-PSP算法提升2 dB以上。

盲分离;单通道;串行干扰抵消;因子图

由于单通道同频混合信号盲分离复杂度较高,运算量较大,因此解决此问题的相关处理方法已成为了研究的热点[1-3],如邻星干扰与抵消、星载AIS突发信号以及成对载波多址(paired carry multiple access,PCMA)信号的盲分离[4]等。单通道同频混合信号盲分离是一类欠定模型求解问题,因此从非协作角度完成处理是非常困难的。基于最大后验概率估计的粒子滤波算法[5-6]与基于最大似然估计的逐幸存路径处理(per-survivor processing,PSP)算法[7-8]在均匀分布的符号序列假设条件下获得了接近最优的性能,但是由于都存在遍历的过程,计算量较大。

Warner等人在文献[9]中指出,若分量信号在成形滤波上存在差异,则采用过采样方法能得到类似多通道接收的效果,即可将目前应用于多输入多输出(MIMO)天线场合的串行干扰抵消(SIC)算法引入到单通道同频混合信号的解调上,降低分离算法复杂度。近年来,基于编码辅助符号序列估计算法以其在参数差异较小以及信噪比较低条件下的优异性能得到了广泛关注。涂世龙等人提出一种基于编码辅助的M-PSP数字调制混合信号单通道盲分离算法,采用卷积编码方式,通过在状态中加入编码约束获得了较未编码更好的分离性能[10]。为解决复杂编码情况的盲分离,栾海妍将因子图模型引入到单通道同频混合信号盲分离中,利用因子图理论在处理复杂多变量函数方面的显著优势,基于粒子滤波算法实现了信噪比较低情况下对混合信号符号序列的有效估计[11],但粒子滤波的使用增加了算法复杂度。

本文在文献[9,11]的基础上,提出了一种基于串行干扰抵消算法与LDPC软信息译码的迭代分离算法。该算法联合解调模块、信息交互模块与译码模块,在解调过程中产生指导译码的先验软信息,译码结果再反馈指导解调,信息交互模块实现解调与译码间信息传递,获得了参数差异较小与信噪比较低时良好的分离性能,且在最大程度上降低了算法复杂度。

1 信号数学模型

不失一般性,本文考虑的混合信号由具有相同频率、时隙或扩频码字相互独立的2路信号混叠而成,即PCMA信号模型。接收信号的复基带模型可表示为

y(t)=A1(t)exp(j(2πΔf1(t)t+θ1(t)))x1(t)+

A2(t)exp(j(2πΔf2(t)t+θ2(t)))x2(t)+v(t)

(1)

式中:A1(t)和A2(t)为接收信号中2路信道的瞬时幅度,Δf1(t)、Δf2(t)和θ1(t)、θ2(t)分别代表2路信号的瞬时频偏与相偏,一般认为这些量都是慢变的,记为A1、A2、Δf1、Δf2、θ1、θ2;v(t)为方差σ2的零均值高斯白噪声。则式(1)可写为

(2)

x1(t)和x2(t)为2路数字基带调制信号,表达式为

(3)

(4)

式中:a1,m和a2,n分别为第1路所发送的第m个和第2路所发送的第n个符号;T1和T2分别为2路发送信号符号周期,由于本文研究的单通道同频混合信号针对2路信号分量符号周期相同情况,因此将T1和T2统一由T表示,它们是独立同分布的;h1(t)和h2(t)分别为2路信号等效信道滤波器,包括成型滤波器、信道滤波器以及匹配滤波器等;τ1和τ2为2路信号的时延。

将式(2)按符号速率进行采样,有

(5)

式中:xi,k(i=1,2)的表达式为

(6)

yk=y(kT);vk=v(kT);hi(t)的持续时间为LT。假定从(1-L1)T到L2T,L=L1+L2,则第i路信号的信道滤波器的第k个抽头系数写为

hi,k=Aiexp(j(2πΔfikT+θi))[hi((L1-1)T+τi),

hi((L1-2)T+τi),…,hi(-L2T+τi)]T

(7)

(8)

因此,接收混合信号可以表示为

(9)

PCMA信号模型可写为

式中:H1和H2分别代表2路信号传输信道;a1和a2分别代表2路信号的发送符号。盲分离算法目的是由接收信号y恢复发送信号a。

2 迭代分离算法

联合SIC与因子图的单通道同频混合信号盲分离算法流程如图1所示。

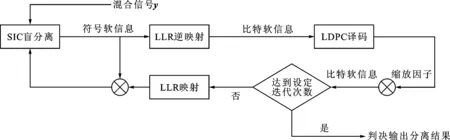
图1 本文算法流程图

2.1 传统SIC解调步骤

针对信号模型y=Ha+v,进行SIC解调。

初始化i=1,首先找到信道矩阵H的广义逆矩阵

(10)

找到当前最佳估计信号位置k

(11)

(12)

式中:(Gi)j表示矩阵Gi的第j行。

估计符号软信息

(13)

量化估计值,消除估计信号在接收信号中影响,更新信道矩阵

(14)

(15)

(16)

i=i+1

(17)

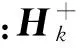
2.2 迭代分离结构

2.2.1 从SIC算法中获得软输出 针对SIC算法,已有文献只将其硬判决的输出作为最终的解调结果,无法充分利用后端译码器的纠错能力。然而,从2.1节中的SIC算法流程可以看出,通过对式(13)的结果进行解映射可获得比特序列的似然软信息un。该软信息一方面指导译码过程输出软信息,另一方面与译码软信息一起指导SIC解调算法实现,通过交互信息传递模块实现解调模块向译码模块的信息传递。

2.2.2 对数似然比交互信息传递 迭代分离算法中解调和译码之间以比特的对数似然比[12](log-likelihood ratio,LLR)形式传递软信息,即解映射过程。本文算法中以QPSK调制信号为例,n时刻发送符号为an,且在不同时刻相互独立。SIC解调产生符号软信息un,如式(13),则有如下统计关系

(18)

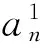
(19)

结合设定星座点信息有

(20)

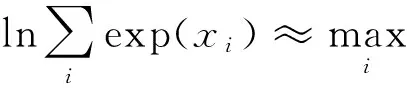
(21)

由式(21)得到n时刻发送符号第1个比特对数似然比,接下来进行归一化得到该比特为1与0的概率分别为

(22)

(23)

式(22)、式(23)为译码过程初始化提供了先验信息。

2.2.3 从LDPC译码中获得软输出 首先介绍LDPC码的Tanner结构[13]。Tanner由节点和边构成,其中节点可分为2种,分别是变量节点z和校验节点c,其个数分别与校验矩阵的行数m与列数n相同。边只能连接不同种类的节点,且满足以下规则:当校验矩阵中第j行第i列元素为1时,称为第j个变量节点zj与第i个校验节点ci相邻,可见一个Tanner图就对应一个LDPC码。

BP算法又称为和积译码算法,“和”指校验节点ci向相邻变量节点zj传递的信息rij,s(s=0,1分别表示该校验节点向变量节点传递的比特“0”信息与比特“1”信息),是对该校验节点的其他相邻变量节点所发信息进行求和运算;“积”指变量节点向相邻校验节点传递的信息qij,s,是对该变量节点的其他相邻校验节点所发信息进行求积运算。具体译码步骤如下[14]。

(2)和运算。校验节点ci向相邻变量节点zj传递信息rij,s的更新计算

(24)

(25)

式中:j′表示所有与校验节点ci相邻的变量节点组成的集合N(i)中除去变量节点zj后剩余的变量节点。

(3)积运算。变量节点zj向相邻校验节点ci传递信息qij,s的更新计算

(26)

(27)

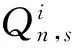
(28)

译码过程会产生指导SIC解调算法的软信息En,该软信息反馈到解调模块,实现译码算法向解调算法的信息传递。下面对本文迭代分离算法步骤做总体详述。

2.3 迭代分离算法步骤

本文迭代分离算法结合了SIC解调算法与LDPC译码算法,2个过程互相为对方提供软信息,使得分离信息越来越准确,具体步骤如下。

(1)SIC解调。利用2.1节SIC解调算法对混合信号yk进行分离,得到符号软信息uk(式(13))。

(2)解映射。对得到的软信息uk进行对数似然比解映射,得到比特软信息fj,s,作为LDPC译码的初始先验信息。

(3)LDPC译码。对步骤2得到的比特软信息进行译码,得到译码结果软信息qij,s,在此基础上得到符号软信息Ek。

(4)迭代判决。若迭代次数小于设定值,则将步骤3产生的软信息Ek代入步骤1中继续进行SIC分离,其中式(13)计算更新为

(29)

式中:d为迭代次;λ为迭代因子。可见随着d增加,可靠的译码软信息影响变大,分离性能变好。若迭代次数达到设定值,则进行步骤5。

迭代因子λ反映了译码软信息在迭代反馈中更新外信息符号所占的比例,随着迭代次数增加,噪声能量在信号中逐渐减小,λd也相应变小来增加译码软信息Ek的比例。研究表明,当λ取值为0.5至0.7时,解调性能最为准确。

3 仿真结果与分析

对本文算法进行仿真。仿真参数:2路QPSK信号混合,采用(360,240)LDPC码以及根升余弦成形,滚降系数为0.35;接收端进行相应的匹配滤波与译码,8倍过采样接收;迭代因子λ为0.5。算法性能以2路误比特率(BER)的平均值来衡量,蒙特卡罗实验次数为50次。

3.1 本文算法性能及对比

参数设置为:2路混合信号的幅度比为1∶0.8;时延差为0.4T(T为符号周期);频偏相偏为0。为了突出迭代效果,同时给出了文献[10]中M-PSP算法、未经迭代时的性能曲线(即由解调后结果直接译码输出)以及信道响应准确设置情况下PSP-MLSE算法的分离性能曲线[15],作为未经译码迭代PCMA信号的盲分离上界。图2给出了不同信噪比下3种算法通过不同迭代次数的分离性能曲线,由图2可见,本文分离算法在2次迭代后性能趋于稳定,与不采用迭代处理算法相比,在误比特率为10-3时经1次迭代就能获得3 dB信噪比增益,经2次迭代则有近4 dB信噪比增益,与文献[10]算法相比性能接近,但是本文采用SIC分离算法,较文献[10]的PSP算法在复杂度上有优势。与PSP-MLSE算法的分离上界相比,误比特率为10-4时经2次迭代也能有近2 dB信噪比增益。结合每一次迭代运算复杂度,利用本文算法对PCMA信号进行盲分离时迭代次数取2次。还可以发现,在信噪比越高时性能提升越明显,这是由于LDPC编译码有译码门限,当错误比特数超出了这个门限译码将失去纠错能力。本文以(360,240)LDPC码为例来研究译码门限。

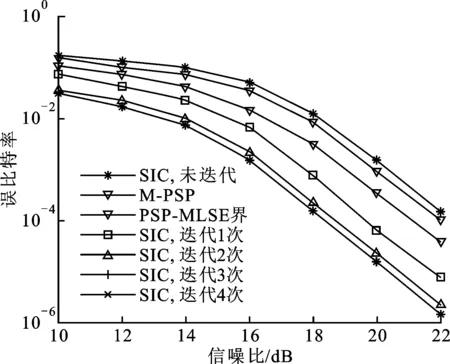
图2 3种算法的性能对比

3.2 译码门限仿真

表1给出了译码前后错误比特数对比,其中码长360bit(含信息码240bit),加入随机错误比特数e1,运行100次得到译码后每帧平均错误比特数e2。实验中随机对译码前码字产生错误,可见含随机错误比特数在28个以内时可以实现完全纠错,而当错误比特数超过40个时译码纠错完全失效。利用该实验可以解释图2信噪比越高时性能提升越明显的原因,即随着信噪比提高,译码前错误比特数减少,使得译码纠错性能提高。

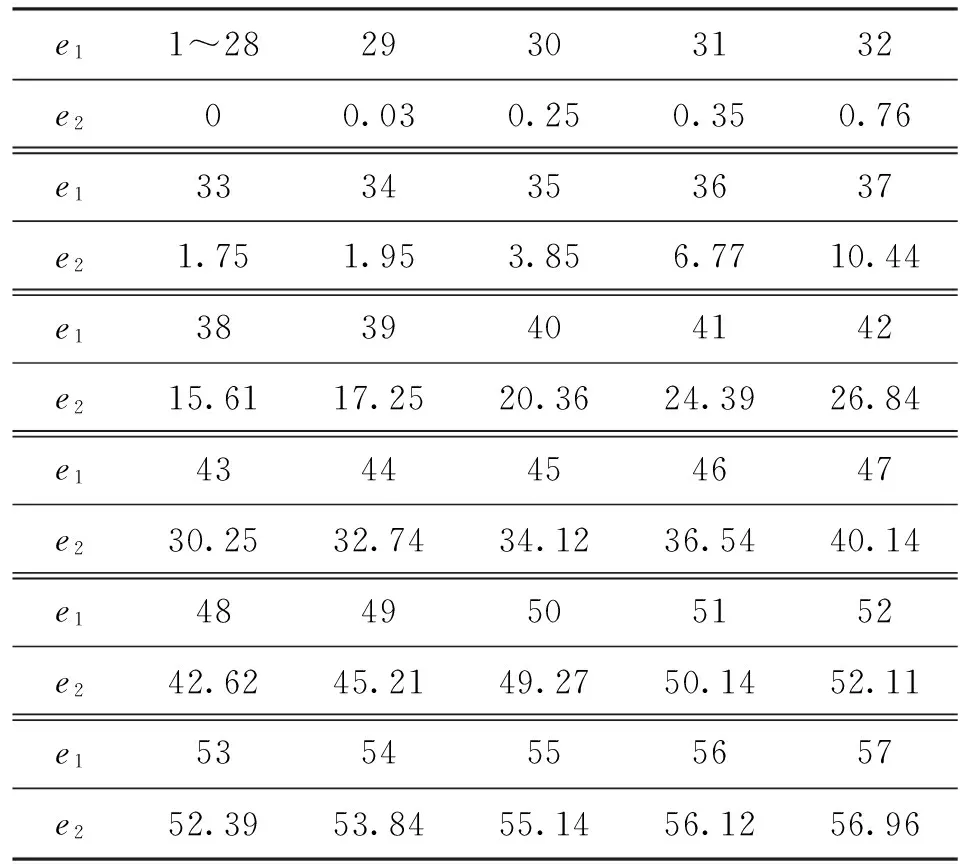
表1 译码前后错误比特数对比

3.3 参数对算法性能影响

图3给出了混合信号不同幅度比下的分离性能曲线,2路混合信号的时延差为0.4T(T为周期)。可见,随着2路信号幅度比值的增加,分离性能也有较大提升,幅度比1∶0.8时的分离性能要比1∶1时提升近2个数量级。

将时延差归一化,图4给出了不同迭代次数下混合信号不同时延差的分离性能曲线。信噪比为20 dB,2路混合信号幅度比为1∶0.8。可见,2路时延差的增加明显地提高了分离性能,时延差越接近0.5,分离误比特率越低,当2路信号时延差小于0.1时,算法将失效。还可以看到,分离误比特率随着迭代次数的增加显著降低,说明本文迭代算法的有效性,当迭代次数2次以上时,分离误比特率将趋于稳定,迭代算法性能达到饱和。

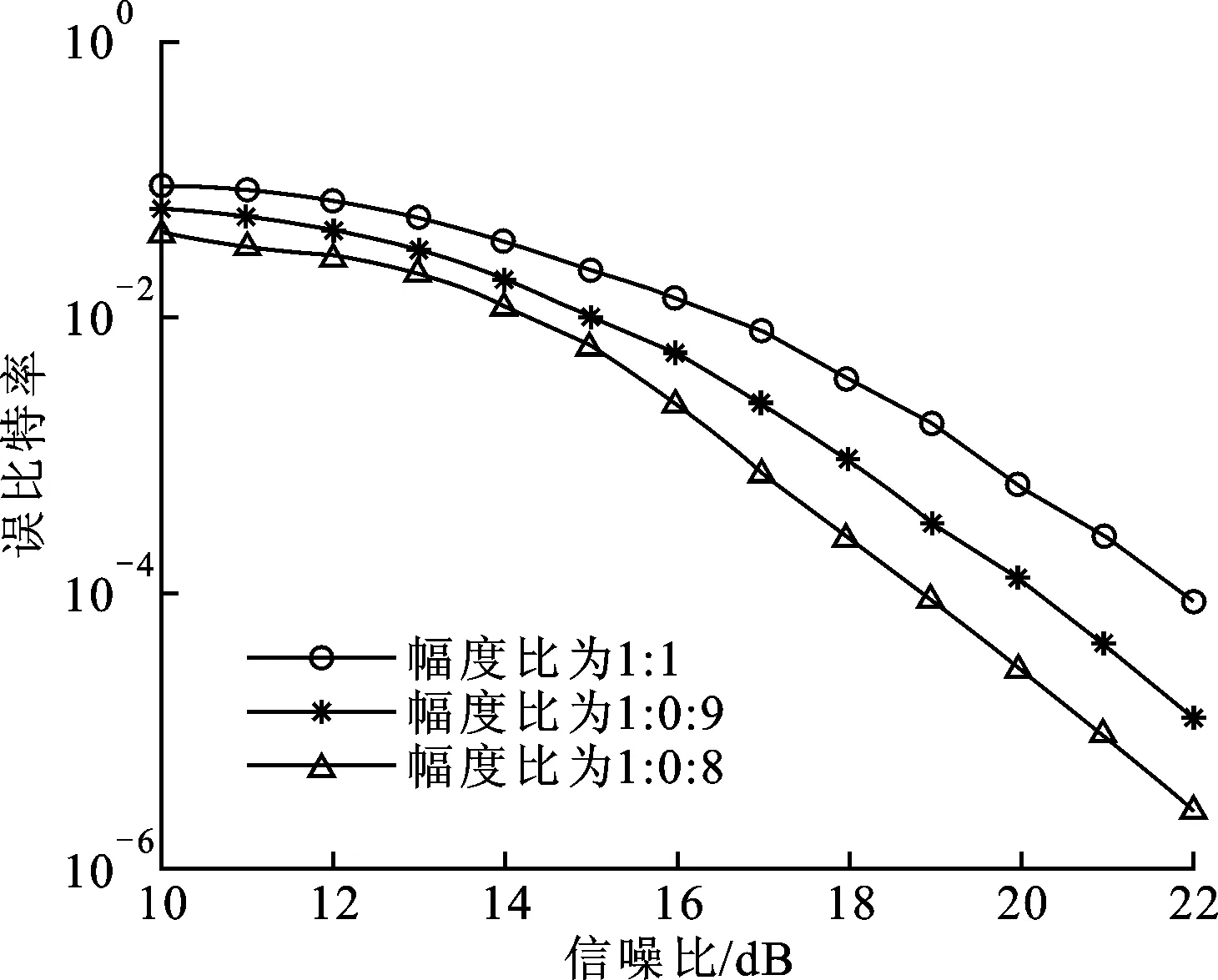
图3 幅度比对本文算法性能的影响

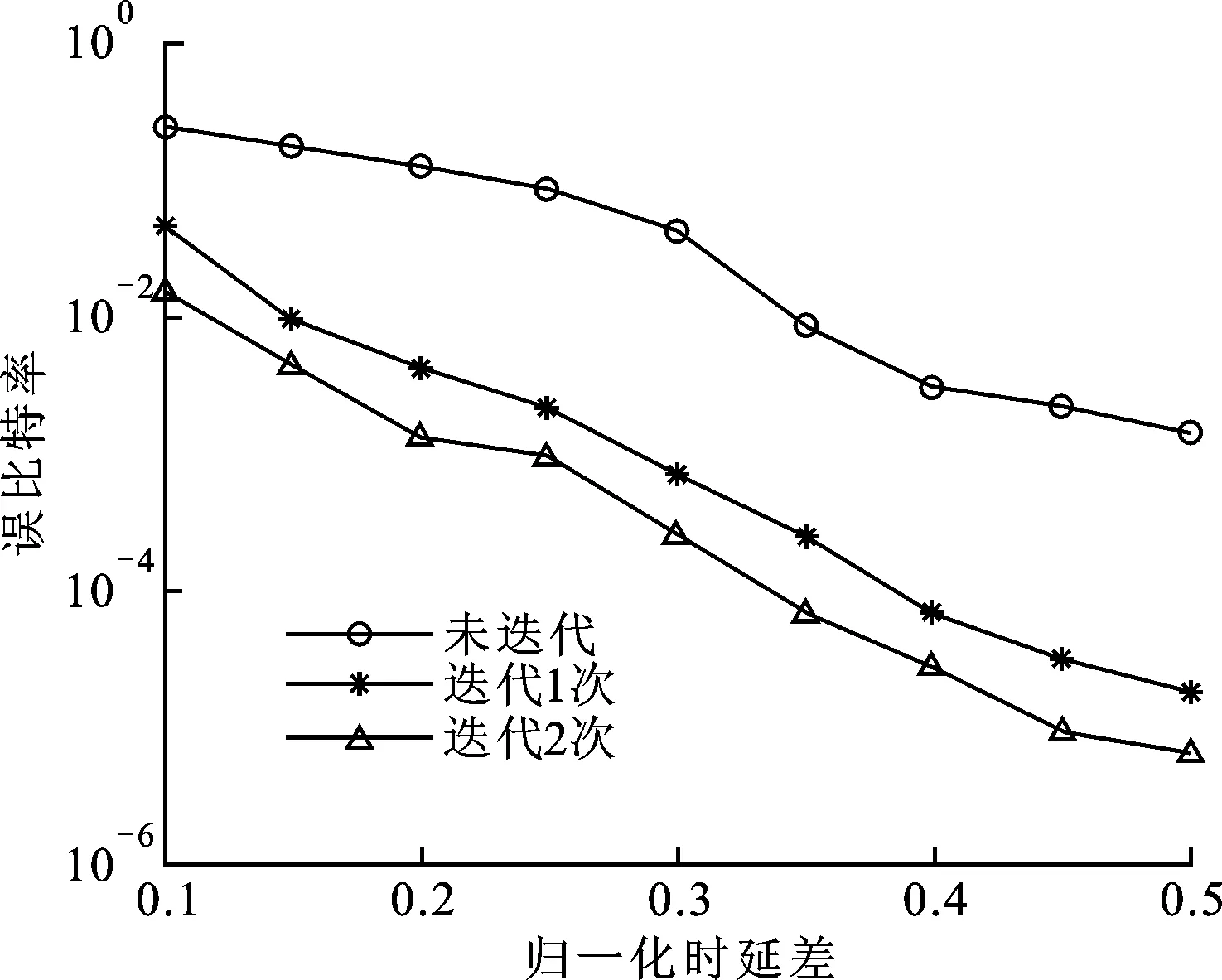
图4 迭代次数对本文算法性能的影响

由分析可知,2路信号幅度比与时延差是影响分离算法性能的主要因素,且当混合信号幅度与时延差别越大分离越准确,这是因为本文算法是基于2路信号的参数差异来实现分离的。由图4还可以看出,本文算法在2路信号参数差异较小时也具有很好的分离性能。

4 结 论

本文算法通过交互信息模块实现解调模块与译码模块间软信息的传递,随着迭代次数的增加,译码模块纠错信息在解调过程中所占比例越来越大,得到的盲分离结果越来越准确。可见本文方法建立在译码模块有效纠错译码基础上,而LDPC译码有一定的译码门限,超出这个译码门限将会造成译码错误增多,反馈回解调使得盲分离算法失效,这是本文算法的局限性,仿真分析中也对此进行了研究分析。

[1] JANG G J, LEE T W, OH Y H. A subspace approach to single channel signal separation using maximum likelihood weighting filters [C]∥IEEE International Conference on Acoustics, Speech and Signal Processing. Piscataway, NJ, USA: IEEE, 2003: 45-48.

[2] TU S, ZHENG H, GU N. Single-channel blind separation of two QPSK signals using per-survivor processing [C]∥IEEE Asia Pacific Conference on Circuits and Systems. Piscataway, NJ, USA: IEEE, 2008: 473-476.

[3] 张冬玲, 杨勇, 李静, 等. 基于Turbo均衡和信道估计的单通道盲信号恢复算法 [J]. 通信学报, 2014, 35(1): 47-53. ZHANG Dongling, YANG Yong, LI Jing, et al. Blind data recovery of single-channel mixed signals based on Turbo equalization and channel estimation [J]. Journal of Communications, 2014, 35(1): 47-53.

[4] 万坚, 涂世龙, 廖灿辉, 等. 通信混合信号盲分离理论与技术 [M]. 北京: 国防工业出版社, 2012: 24-29.

[5] 张冬玲, 张君, 李静, 等. 基于BICM-ID系统的单通道混合信号盲恢复算法 [J]. 系统工程与电子技术, 2012, 34(2): 379-384. ZHANG Dongling, ZHANG Jun, LI Jing, et al. Blind data recovery of single-channel mixed signals based on BICM-ID [J]. Systems Engineering and Electronics, 2012, 34(2): 379-384.

[6] 崔荣涛, 李辉, 万坚, 等. 一种基于过采样的单通道MPSK信号盲分离算法 [J]. 电子与信息学报, 2009, 31(3): 566-569. CUI Rongtao, LI Hui, WAN Jian, et al. An over-sampling based blind separation algorithm of single channel MPSK signals [J]. Journal of Electronics & Information Technology, 2009, 31(3): 566-569.

[7] MOHAMMAD M, TRANTER W. Blind acquisition of short burst with per-survivor processing [J]. IEEE Transactions on Wireless Communication, 2007, 6(2): 429-432.

[8] 廖灿辉, 涂世龙, 万坚. 基于迭代的同频混合信号单通道盲分离/译码算法 [J]. 通信学报, 2011, 32(8): 111-117. LIAO Canhui, TU Shilong, WAN Jian. Iterative algorithm on single-channel blind separation and decoding of co-frequency modulated signals [J]. Journal on Communications, 2011, 32(8): 111-117.

[9] WARNER E S, PROUDLER I K. Single-channel blind signal separation of filtered MPSK signals [J]. IEE Proceedings of Radar, Sonar and Navigation, 2003, 150(6): 396-402.

[10]涂世龙, 陈越新, 郑辉. 利用纠错编码的同频调制混合信号单通道盲分离 [J]. 电子与信息学报, 2009, 31(9): 2113-2117. TU Shilong, CHEN Yuexin, ZHENG Hui. Exploiting error-control codes in single-channel blind separation of co-frequency modulated signals [J]. Journal of Electronics & Information Technology, 2009, 31(9): 2113-2117.

[11]栾海妍. 同频混合信号盲分离若干关键技术研究 [D]. 郑州: 解放军信息工程大学, 2011.

[12]张冬玲, 张君, 李静, 等. 一种基于Turbo迭代处理实现PCMA信号盲恢复算法 [J]. 武汉大学学报: 理学版, 2011, 57(5): 383-388. ZHANG Dongling, ZHANG Jun, LI Jing, et al. A blind data recovery of PCMA signals based on the Turbo iterative processing [J]. Journal of Wuhan University: Natural Science Edition, 2011, 57(5): 383-388.

[13]LOELIGER H A. An introduction to factors graphs [J]. IEEE Signal Processing Magazine, 2004, 21(1): 28-41.

[14]赵刚. 扩频通信系统实用仿真技术 [M]. 北京: 国防工业出版社, 2009: 164-172.

[15]廖灿辉, 万坚, 周世东. 两同频调制信号混合单通道盲分离的性能界 [J]. 清华大学学报: 自然科学版, 2010, 50(10): 1646-1650. LIAO Canhui, WAN Jian, ZHOU Shidong. Single-channel blind separation performance bound of two co-frequency modulated signals [J]. Journal of Tsinghua University: Science and Technology, 2010, 50(10): 1646-1650.

(编辑 刘杨)

A Blind Separation Algorithm of Single-Channel Signals Based on Serial Interference Cancellation and Factor Graphs

GUO Yiming,PENG Hua,ZHANG Dongling,YANG Yong

(Institute of Information System Engineering, Information Engineering University of PLA, Zhengzhou 450001, China)

An iteration processing algorithm based on serial interference cancellation(SIC) and factor graph decoding is proposed to solve the high complexity problem of blind separation of single-channel co-frequency signals in complex coding. The forward channels are reconstructed based on the transmission channel parameters. Then, the SIC demodulation is completed under the premise of the channel reconstruction to obtain the soft information and to pass the information to the decoding module. The separation performance is improved with decoding gain feedback. Focuses are laid on the information interaction between demodulation and decoding, and the impact of the difference between channel parameters of signal components of two channels on the performance of demodulation. It is concluded that the separation performance of the algorithm is improved when the number of iterations increases and the difference of channel parameters increases. Simulation results and a comparison with the M-PSP algorithm with LDPC codes show that the proposed algorithm obtains a gain of about 2 dB in signal-noise ratio for QPSK signals after two iterations.

blind separation; single-channel; serial interference cancellation; factor graph

2015-01-22。

郭一鸣(1990—),男,硕士生;彭华(通信作者),男,教授,博士生导师。

国家自然科学基金资助项目(61401511)。

时间:2015-07-23

10.7652/xjtuxb201510021

TN911.7

A

0253-987X(2015)10-0130-06

网络出版地址:http://www.cnki.net/kcms/detail/61.1069.T.20150723.0922.006.html