数学法测量非碎裂性骨干骨折断端旋转度的CT实验研究
作者单位:611730 成都,四川省成都市郫县中医医院放射科
数学法测量非碎裂性骨干骨折断端旋转度的CT实验研究
作者单位:611730 成都,四川省成都市郫县中医医院放射科
刘荣,丁祥华
[摘要]目的探讨在MSCT-MPR图像中,依据三角函数原理及勾股定理测量非碎裂性骨干骨折断端旋转度的可行性。方法将5根猪股骨折断后,分别将两断端固定在一个自制的模拟骨折旋转架上,在一侧断端旋转10°、30°、50°、70°、90°、110°、130°、150°、170°时,分别行MSCT薄层扫描、进行MPR重建,在图像中找到能体现两断端解剖对位的定位点,测量定位点在不同方位与中轴线的距离,依据三角函数原理及勾股定理计算出旋转度数,将计算数据与实际值对比分析。结果在以上9个旋转度下,5根猪股骨断端计算所得数据与实际值均较为接近,差值均在10°以内,差异无统计学意义(P>0.05)。结论在非碎裂骨干骨折MSCT-MPR图像中,可清楚显示定位点,依据数学原理可准确测量其旋转度。其计算过程通过程序化处理,简便、快捷,能为临床医生提供以往无法获得的折端旋转度信息,并为PACS软件工程师开发出骨折端旋转度测量工具提供理论支持。
[关键词]股骨;数学方法;测量;骨干骨折;旋转度
外伤骨折患者,由于其受力方式的复杂多样及受断端周围肌腱、韧带的作用力影响,骨折端常有不同程度的错位、成角或旋转[1],在常规X线摄片中,折端的错位、成角程度常常一目了然,并且医生能轻易测量出具体数据。而对骨折端旋转程度的评估缺乏统一的认识,全凭个人经验大致估计,国内外文献鲜有对折端旋转度的量化分析报道。本研究试图在多层螺旋CT(MSCT)的多平面重建(MPR)图像中寻找到能准确反映两断端解剖对位的点,通过分析这些点的位置信息,运用数学方法计算出两断端旋转度。
1材料与方法
1.1测量理论依据骨折端旋转可以理解为:断面上任意一点绕中轴线的旋转,在MPR冠状位与矢状位图像上表现为任一点与中轴线的距离发生变化,通过这个距离变化,可间接了解骨折端的旋转情况。同时,由于受力大小、方向和骨组织结构等因素影响,折断面显示粗糙不平[1],CT多方位图像可清晰显示这一特点(图1),而两断端的最高点H1、H2或最低点L1、L2是最易识别、最能体现两断端解剖对位的点。故测量上述点位与中轴线距离变化,以了解骨折端旋转情况是可行的。
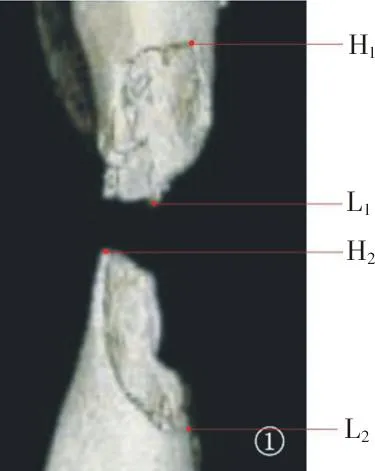
图1 骨折断面CT重建图像
1.2模型制作准备好完整的猪股骨若干,人为暴力折断后选取无碎骨片的5组(1组即为1根猪股骨的两个折断端)作为实验对象;每组均将两断端分别固定在一个自制的模拟折端旋转模型上,该模型能使其中一端完全固定,另一端能按1°的精度旋转0~360°。
1.3CT扫描方法及测量平台采用飞利浦荣耀MX4000Dual螺旋CT扫描仪,行常规轴位平扫,层厚2.5 mm,层距2.5 mm,管电压100 kV,电流80 mA。测量工作平台为INFINITT PACS报告客户端。将5组骨折断端模型先后置于CT扫描架,分别将断端旋转10°、30°、50°、70°、90°、110°、130°、150°、170°行薄层扫描,并进行MPR重建。
1.4测量及计算方法(1)选择定位点:在横断位图像中找到骨折断面的最低点L1、L2或最高点H1、H2。本实验为统一标准,均选取最高点H1、H2。将断面所在层面的中心点标为O1、O2。(2)测量距离:在MPR图像中,通过定位线跟踪、关联等,可以轻易测得H1、H2与骨干冠状面和矢状面的距离,设点H1、H2与骨干矢状面的距离分别为x1、x2,与骨干冠状面的距离分别为y1、y2(图2-7)。(3)建立坐标系:将点H1、H2所在层面的横断面进行模拟重叠,可以画出坐标轴,其中X轴代表冠状线,Y轴代表矢状线,在坐标上标明方位(前、后、内、外),则点H1的横断位坐标为(±x1,±y1),点H2的横断位坐标为(±x2,±y2)。至此,即可以通过角度测量工具测得定位点H2相对于H1的旋转方向和度数(图8)。
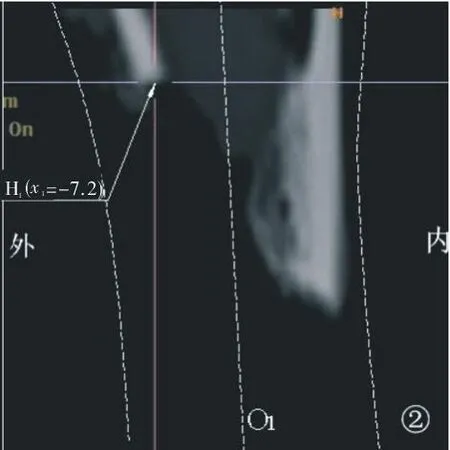
图2 近折端经断面最高点H1的冠状位图像
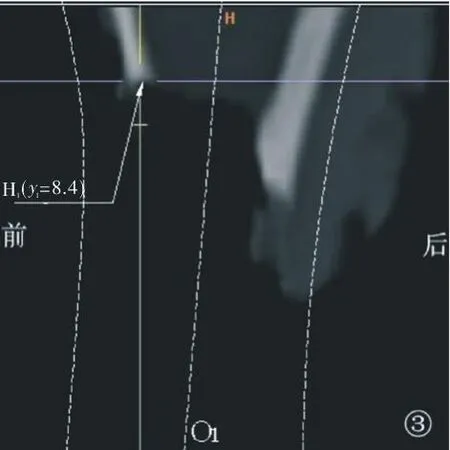
图3 近折端经断面最高点H1的矢状位图像

图4 近折端经断面最高点H1的横轴位图像

图5 远折端经断面最高点H1的冠状位图像
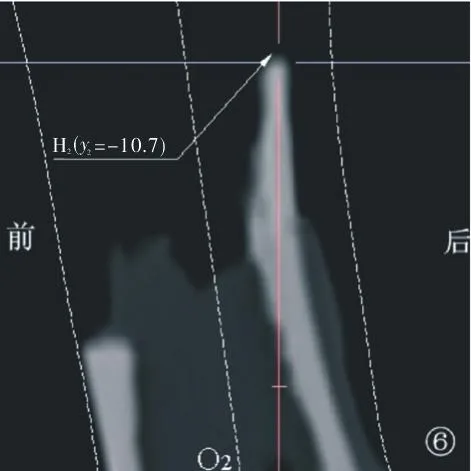
图6 远折端经断面最高点H1的矢状位图像

图7 远折端经断面最高点H1的横轴位示意图

图8 旋转度测量示意图
将两断端横轴位中线重叠,提取点H1、H2坐标信息,标注于坐标系内,由此可直接测得旋转度
1.5程序化处理如果按上述方法测量,则显得繁锁与抽象,故而引入数学方法,将以上第(2)、(3)步改由如下计算步骤代之。由余弦定理得:
(公式1)
由勾股定理得:
(公式2)
(公式3)
(公式4)
由反三角函数公式得:
∠H1OH2(弧度)=arccos∠H1OH2
(公式5)
将弧度值转换为角度:
∠H1OH2(角度)=arccos∠H1OH2×180/π
(公式6)
可见,只要知道x1、x2、y1、y2的值(定位点与中线的距离),就能求出旋转度数∠H1OH2。虽然上述公式计算量较大,但如果利用计算机强大的计算功能,将大幅提高效率,比如利用常用的Excel软件中的单元格函数插入功能、VB或C++等面向对象的程序设计等,将以上计算过程交由计算机,只要分别输入x1、x2、y1、y2的值,可即刻得到折端度数。旋转方向的判断则只需要进行相应的坐标显示就可实现。
1.6统计学方法采用Microsoft Excel 2003对数据进行统计学处理。同一组股骨断端在不同旋转度数下的计算值与实际值之间的差异显著性检验采用成对二样本双侧t检验;各组计算值均数间的差异显著性检验采用随机区组设计的单因素方差分析,显著性检验水准α=0.05。
2结果
程序计算所得数据与实际值非常接近,在共计45次的测量中,测量值与实际值差距均在10°以内,其中差距在1°以内的有1次,1~5°有35次,5~10°有9次。统计分析结果表明,各组间比较,在不同旋转度下测量值间的差异无统计学意义(F=0.001,P>0.05)。同一组内不同旋转度下的测量值亦无显著差异,见表1。

表1 数字方法计算数值与实际值比较
注:P1表示同一组内不同旋转度数下计算值与实际值之间的差异t检验概率
3讨论
一般而言,对一个骨干骨折患者行放射学检查的目的在于测量断端对位、对线,以利于临床医生选择适当的治疗方式,医生常能根据X线片所提示断端错位、成角情况进行手术或手法复位。但常规X线摄片无法准确测量折端的旋转度,只能按一般规律大致估计。如存在骨折两端不等宽、一侧骨皮质密度增加或增厚、折断面背靠背现象、一侧关节头形态变化等情况[2-3],骨科医生通常使用牵引、反向旋肢等方式予以矫正,但这种矫正总是在摸索中进行的,缺乏量化依据,在临床治疗中风险性较大。
本研究所使用的计算方法,不需要顾及一侧关节头形态,只需在折断面找到定位点,并测量定位点与中线的垂直距离(x1、x2、y1、y2),依据三角函数原理、勾股定理,经程序化计算,可快速得出旋转度数。理论上,这一数学原理可以毫无误差地体现折端旋转度,但在本实验结果中,均呈现误差。分析产生误差的原因可能有:(1)肉眼确定的定位点并不是数学意义上的点,而仅是一个面积足够小的面而已,由此导致选择定位点和测量时的误差;(2)骨干的横断面不规则,导致定位点沿长骨中轴线旋转的动点轨迹不是圆形,故仅从两个方位(冠状和矢状)来确定定位点的坐标存在误差。为了解上述因素对计算结果的影响程度,我们将计算所得数据与实测值进行比较,显示二者差异无统计学意义(P>0.05),说明以上因素对计算结果的影响不大。另外,在测量中需要注意的是:骨折断端向一侧旋转n°与反方向旋转(360-n)°的断面形态是一致的。因此,在判断旋转方向时,结合临床体征依然重要。
综上认为,此数学方法测量骨折端旋转度在临床上具有可行性,一方面能为临床医生提供以往无法获得的折端旋转度量化信息;另一方面,也能为PACS软件工程师开发出骨折端旋转度测量工具提供理论支持,在安装有此工具的影像工作站上,或许能对非碎裂性骨干骨折断端旋转度进行常规测量,使之更好地服务于临床工作,最大限度减低临床治疗风险。
【参考文献】
[1]王以进,王介麟.骨科生物力学[M].北京:人民军医出版社,1989:193.
[2]阳治兵.骨折断端旋转移位在X片上的辨识[J].内蒙古中医药,2010,1(4):110.
[3]Gottschalk HP,Bastrom TP,Edmonds EW.Reliability of internal oblique elbow radiographs for measuring displacement of medial epicondyle humerus fractures:a cadaveric study[J].J Pediatr Orthop,2013,33(1):26-31.
CT experimental study on rotation degrees of broken ends of bones of non-comminuted fracture measured by mathematical method
Liu Rong,Ding XianghuaDepartment of Radiology,Pixian Hospital of Traditional Chinese Medicine,Chengdu,Sichuan,611730,China
[Abstract]ObjectiveTo explore the feasibility for measuring the rotation degrees of the broken ends of bones of non-comminuted fracture on the principle of trigonometric function and Pythagoras theorem in MSCT-MPR image.MethodsFive pig femoral bones were broken off,and both broken ends were fixed to a self-made simulating fracture rotation frame,respectively;and then,the broken ends on one side were rotated to 10°,30°,50°,70°,90°,110°,130°,150°,and 170°,respectively;MSCT thin-layer scanning and MPR reconstruction were carried out,and the positioning points showing the anatomic directions of both broken ends were found in order to measure the distance between the positioning points and the central axes in different directions;lastly,the rotation degrees were calculated on the principle of trigonometric function and Pythagoras theorem,and a comparative analysis was made for the calculation results and the actual values.ResultsIn the above nine rotation degrees,the calculation results of the five pig femoral bones were approximate to the actual values,and the differences were all within 10°,having no significant difference(P>0.05).ConclusionIn the MSCT-MPR images of bones of non-comminuted fracture,the positioning points may be shown clearly and the rotation degrees of the broken ends may be measured with mathematical method;the process of calculation may be processed by programs fast and easily,so as to provide information about the rotation degrees of the broken ends and theoretical support for PACS software engineer to develop tools to measure the rotation degrees of the broken ends of bones.
[Key words]femoral bones;mathematical method;measurement;bone fracture;rotation degree
(收稿日期:2014-09-15)
文章编号1004-0188(2015)02-0137-05
doi:10.3969/j.issn.1004-0188.2015.02.009
中图分类号R 683.4
文献标识码A
通讯作者:刘荣,电话:15328093560;E-mail:351156359@qq.com

