输电导线覆冰生长及影响因素数值分析模型
朱永灿,黄新波,,贾建援,田毅,林淑凡
(1.西安电子科技大学机电学院, 710071, 西安;2.西安工程大学电子信息学院, 710048, 西安)
输电导线覆冰生长及影响因素数值分析模型
朱永灿1,黄新波1,2,贾建援1,田毅1,林淑凡2
(1.西安电子科技大学机电学院, 710071, 西安;2.西安工程大学电子信息学院, 710048, 西安)
针对现有输电线路覆冰生长模型仅注重覆冰生长量、难于准确预测覆冰形貌的问题,建立了输电导线局部冰层增长计算模型。采用空气动力学方程求解覆冰导线周围气流场参数、覆冰表面对流换热系数,进而采用欧拉二相流模型计算覆冰导线表面过冷却液滴碰撞系数;建立包含液滴碰撞、溢流、蒸发、升华等因素的质量平衡方程,基于此方程推导出计算对象热量平衡方程,并采用多级假设、一维搜索求解方程中多个未知量,得出各单元的冻结系数和覆冰质量。算例表明:局部碰撞系数及碰撞区域随风速的提高快速增大,覆冰量相应增大;而环境温度及导线电流的增加使得溢流水出现,覆冰类型由雾凇向雨凇过渡;模型所得覆冰形貌和覆冰量与已有实验结果基本相符,计算结果满足电力系统工程需要。
输电线路;覆冰;数值模型;两相流模型;质量平衡
覆冰作为一种特殊的气象现象,给世界各地的架空线路安全运行造成严重影响,加拿大、挪威以及我国都曾遭受灾难性的覆冰事故,其中挪威1961年覆冰事故中椭圆形覆冰的最大截面直径达到了1.4 m,1 m导线的覆冰质量达到了300 kg[1-2]。2008年初,我国南方地区发生长时间冻雨覆冰灾害,仅220 kV以上杆塔受损1 500多基,经济损失超千亿元[2-3]。
为此,国内外科研人员针对电力系统覆冰进行了大量研究。Makkonen模型将覆冰生长分解为过冷却液滴的碰撞、捕获、冻结3部分,通过热量平衡方程对覆冰生长参数进行分析[4-5],该思路为覆冰生长分析以及以热平衡为基础的防、融冰技术发展奠定了基础。蒋兴良等人多年来一直从事输电线路的覆冰理论及试验研究[6-7],在输电线路抗冰设计等方面取得了大量研究成果。黄新波等基于覆冰监测数据,采用灰色理论等智能算法,量化各气象参数对覆冰生长的影响,进行覆冰增长预测[8-10]。郝艳捧等针对电力绝缘子覆冰生长开展仿真模型与试验分析[11-12]。梁曦东等分别建立覆冰生长仿真分析方法,对导线覆冰生长过程进行数值研究[13-14]。上述研究大都将覆冰导线视为一个整体,忽略了溢流水、导线焦耳热、导线温度等因素对覆冰局部生长的影响,预测模型仅注重了覆冰生长量,不能准确预测覆冰形貌,而覆冰形貌决定了气流场、过冷却液滴碰撞系数、热平衡等覆冰生长直接影响因素,因此上述方法必然存在计算误差。
本文以局部质量平衡和热量平衡作为覆冰增长分析依据,采用多级假设、一维搜索的方法得到各单元的冻结系数、溢流水质量等参数,进而得到随时间变化的覆冰质量、覆冰形貌,有助于提高覆冰的预测精度。
1 输电导线结冰过程数值模拟方法
1.1 覆冰生长计算模型
输电线路覆冰过程涉及到多门学科的交叉,如流体力学、传热学、结构力学等,建立完善的覆冰增长模型是非常困难的。覆冰导线表面局部单元k随时间的冰层增量可表示为
(1)
式中:Ik=mim,k+mfi,k-mes,k为进入到单元内的过冷却水质量,mim,k为过冷却液滴的碰撞质量,mfi,k为其他单元流入的液态水质量,mes,k为单元内蒸发、升华引起的质量损失;a3,k为冻结系数。
1.2 覆冰生长计算流程
覆冰生长求解过程可分解为空气流场求解、表面过冷却液滴碰撞系数计算、冻结系数计算、覆冰外形生成4个部分,模拟流程如图1所示。
2 空气及液滴流场数值求解
2.1 空气流场求解
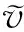
(2)

2.2 欧拉二相流碰撞模型
液滴流场的计算主要有拉格朗日法和欧拉法。欧拉二相流模型基于多相流思想,将液滴视为连续相,采用体积分数描述流体的含水量,并在气流流场求解基础上求解水滴碰撞,不需要计算单个水滴的位置和轨迹,避免了大量的插值计算。过冷却液滴运动的连续性方程和动量方程为[16]
(3)
(4)
式中:a为空气中液滴的体积分数;V为水滴的速度矢量;Va为空气的速度矢量;K为惯性参数;Red为过冷却液滴的雷诺数;CD为阻力系数;ρw为液滴密度;Fr为弗劳德数;g为重力加速度。
覆冰导线的局部液滴碰撞系数为
(5)
式中:a∞为来流初始液滴体积分数;V∞为来流速度;n为单元的表面法向量。
3 输电导线覆冰生长模型及其求解
3.1 覆冰过程溢流水
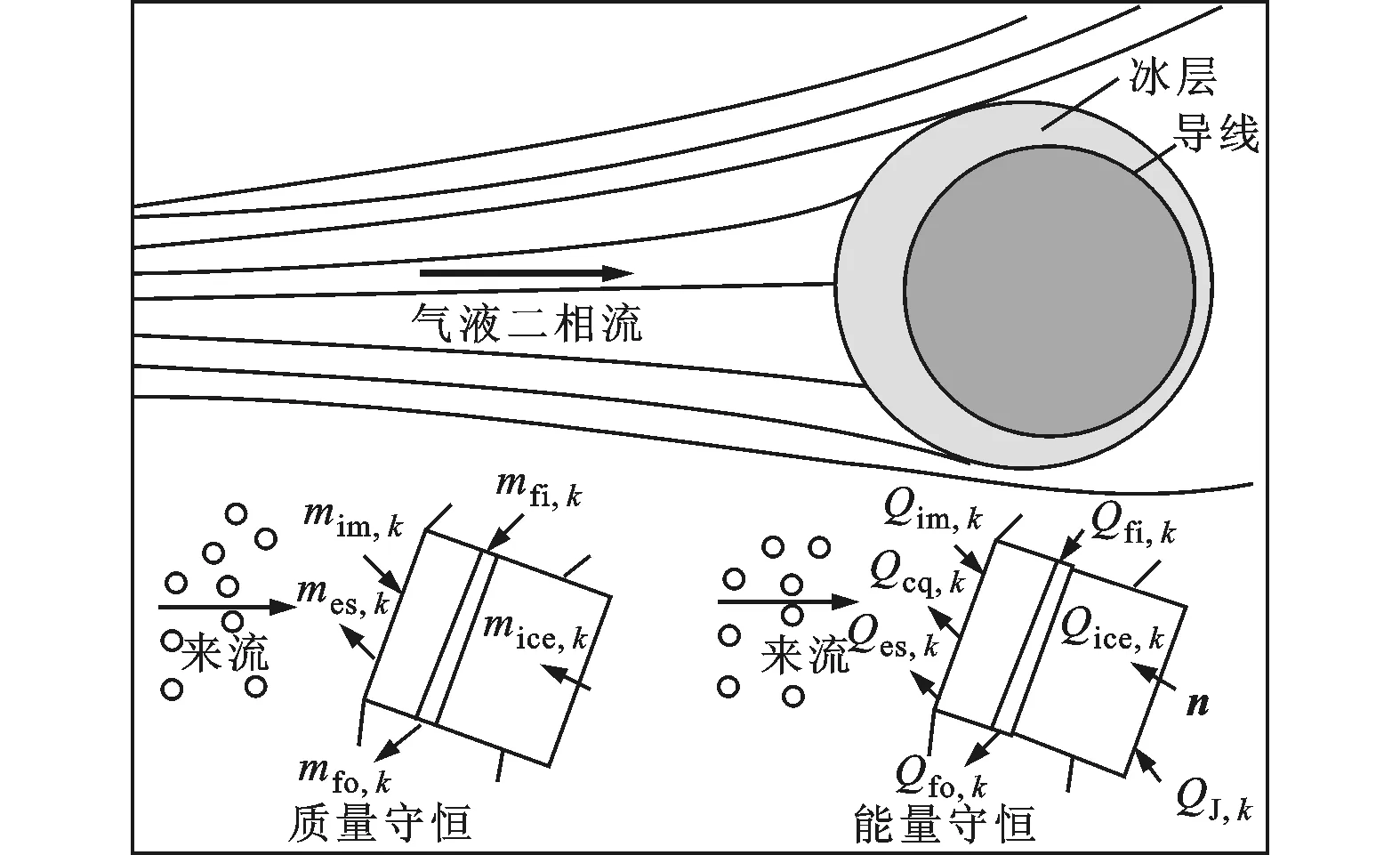
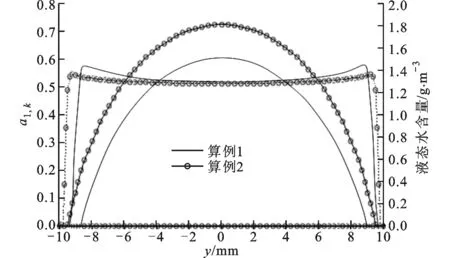
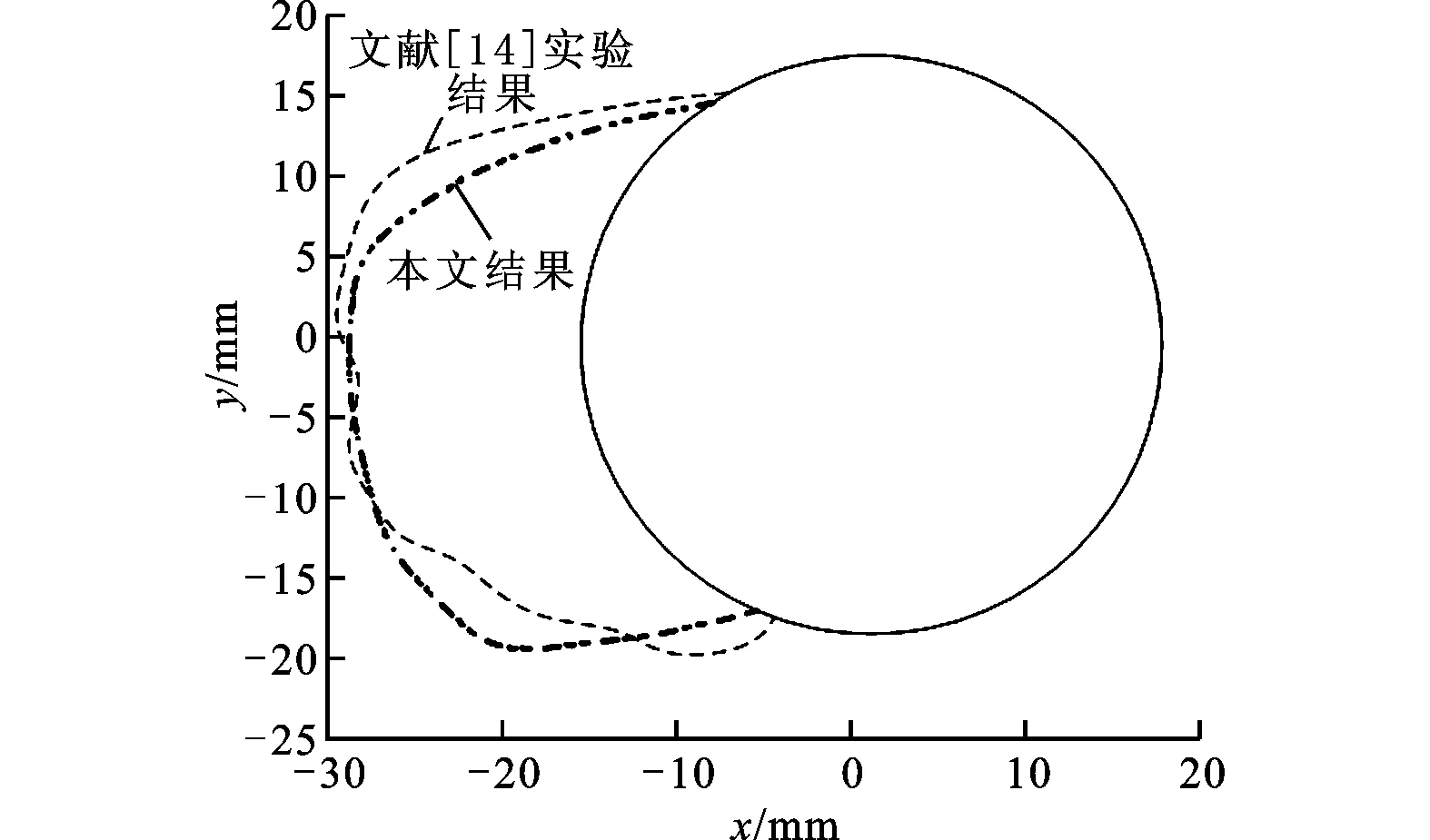
如果区域内过冷却液滴与覆冰表面发生碰撞后全部冻结,没有溢流水发生,则认为覆冰局部干增长,形成的覆冰为雾凇,有a3,k=1、Tw,k<0 ℃(Tw,k为单元k的壁面温度)成立;如果局部区域内液滴未完全冻结,有溢流水存在,则认为覆冰湿增长,形成雨凇,有0 图2 覆冰过程过冷却水溢流示意图 3.2 结冰过程中的质量平衡及能量平衡 3.2.1 质量平衡方程 如图3所示,单元k的质量守恒方程为 (6) 式中:mfo,k为单元内流出的液态水质量;mice,k为单元k最终冻结成冰的质量。 式(6)中变量之间的关系为 (7) 式中:a3,k为局部冻结系数;w为单位体积空气液态水质量;Ak为单元冰面面积;τ为水蒸气与干空气分子质量比;hk为局部对流换热系数;ew,k为壁面温度对应的饱和蒸汽压;ef为环境温度对应的饱和蒸汽压;cf为空气定压比热容;pf为静态空气压强;a2,k为局部单元液滴附着系数。覆冰过程中,过冷却液滴与冰面发生有效碰撞时,液滴迅速冻结,只有极少量发生反弹;当冰层表面有水层存在时,液滴会在表面铺开或者粘附,一般不会发生反弹,因此通常认为a2,k≈1。 3.2.2 能量平衡方程 单元内覆冰生长过程热平衡方程可表示为[17-18] Qcq,k+Qes,k+Qfo,k+Qice,k+Qim,k+Qfi,k+QJ,k=0 (8) 式中:Qcq,k为单元表面与空气换热、热辐射损失;Qes,k为单元表面蒸发、升华热量损失;Qfi,k、Qfo,k分别为单元流入、流出的溢流水引起的能量变化;Qice,k为液滴冻结释放的潜热;Qim,k为碰撞到结冰表面的液滴引起的能量变化;QJ,k为传导到结冰单元的导线焦耳热。 Qcq,k包含了对流换热损失和热量辐射损失两部分,计算公式为[17-19] (9) 式中:Tf为流体温度;δ为结冰表面相对于黑体的总辐射系数;σ为斯忒藩-玻尔兹曼常数。 图3 覆冰过程热量、质量平衡示意图 由过冷却水滴碰撞引起的能量变化主要包含两个方面:一是过冷却液滴附着后温度升高到参考温度引起能量变化;二是液滴撞击后速度变为0,液滴动能的转化。其表达式为 (10) 式中:cw为液滴定压比热容;T0=0为参考温度。 流入单元的溢流水带来的是热量变化,即 (11) 导线负荷电流产生一定的焦耳热,并通过冰层传导到覆冰表面。由于铝质导线的导热率很高,可以认为导线本体各处温度相同,圆筒形覆冰导线传输到单元k的热量可表示为 (12) 式中:Tc为导线温度;rc为导线半径;λi为覆冰层的热导率;ri,k为当前覆冰层厚度,其值由每次覆冰厚度增加量叠加得到;A为冰面总面积。 覆冰过程为准热平衡过程,假设在覆冰过程中导线及冰层温度不变,导线焦耳热全部通过冰层传输到覆冰表面,各单元总的热传导值可表示为[6] (13) 式中:I为导线负荷电流;RAC,Tc为温度是Tc时的导线交流电阻。 液滴冻结成冰的过程中释放大量潜热,并逐渐与壁面温度达到一致,因此Qice,k包含了冻结潜热与冰层降温两种热量变化,可表示为 (14) 式中:Lice为冰的冻结潜热;cice为冰的定压比热容。 流出的溢流水引起的能量损失 (15) 升华和蒸发引起的热量损失 (16) 式中:Les为蒸发潜热。 3.3 能量平衡方程求解 将式(9)~(16)带入式(8),得 mfi,kcw(Tw,k-1-T0)+cwmim,k(Tf-T0)+ mice,kcice(T0-Tw,k)-mfo,kcw(Tw,k-T0)=0 (17) 式(17)中hk、mim,k通过空气流场及液滴流场获得,mice,k、mfo,k可由a3,k、mfi,k表示,所以式(17)是关于a3,k、mfi,k、Tw,k、Tw,k-1、Tc5个未知量的方程,无法直接求得解析解,因此采用多级假设、一维搜索的方法进行求解,计算步骤如下。 (2)k=1时该单元没有溢流水和液滴撞击,有mim,k=0,mfi,k=0,mice,k=0成立,转步骤(3)。 (3)假设单元中液滴部分冻结,单元内覆冰湿增长,Tw,k=T0,根据热平衡方程求解a3,k,转步骤(4)。 (4)根据a3,k的值,存在3种情况:0 通过上述步骤可得各单元的结冰质量,进而根据Macklin密度模型求得单元的覆冰体积增量。 算例1:选用LGJ210/25导线为覆冰对象(简化为等直径光滑圆柱),直径19.98 mm、20 ℃时直流电阻率为0.138 0 Ω/km,假设覆冰时的大气压强为101.325 kPa,环境温度为-15 ℃,风速为5 m/s,气流方向与导线走向垂直,攻角为0°,空气中液态水含量(LWC)为1.2g/m3,液滴中值直径(MVD)为35 μm,导线电流为0。 算例2:保持算例1条件不变,设置流场温度为-4 ℃,风速为10 m/s,导线负荷电流为150 A。 在未覆冰条件下,算例1、算例2导线表面局部单元的a1,k及LWC分布如图4所示。受导线阻尼作用影响,导线迎风侧各处的液滴分布差异很小,导线背风侧LWC为0,LWC最大值出现在气流分离点附近且在气流分离点之后迅速降低为0。a1,k沿y轴大致呈抛物线形状,最大值出现在迎风侧驻点处。与算例1相比,算例2气流分离点后移,过冷却液滴发生有效碰撞的区域增大,迎风侧LWC值略有下降,但液滴的动量增大使其更容易与导线发生有效碰撞,a1,k相应增加。 图4 未覆冰导线a1,k及液态水含量分布 如图5所示,算例1空气温度低,过冷却液滴与导线发生有效碰撞后迅速冻结,没有溢流水产生,生成雾凇覆冰,冰形大致呈现x轴对称。算例2环境温度高,导线电流产生一定的焦耳热,液滴与导线发生碰撞后不能迅速冻结,产生溢流水,生成的覆冰主要为雨凇,未冻结液体由上至下流动,覆冰增长向y轴负方向偏移。 图5 算例1、算例2在10 min时覆冰冰形 算例3:为了与文献[14]结果进行对比,选择与其相同的覆冰条件,各参数为:导线直径为34.9 mm,导线电流为0 A,环境温度为-5 ℃,风速为10 m/s,LWC为1.8 g/m3,液滴中值直径为26 μm。本文数值模拟与文献[14]30 min时结果如图6所示。本文液滴发生有效碰撞区域略小于文献[14]结果,覆冰区域稍小;另外,由于本文规定了未冻结液滴的溢流方向,得到的冰形轮廓更加圆滑。总体来说,本文数值模拟结果与文献[14]冰层厚度及轮廓基本一致,覆冰量误差小于6%。 图6 算例3在30 min时覆冰冰形 (1)基于质量平衡和热量平衡方程建立了输电导线局部覆冰增长仿真模型。增加溢流水、覆冰表面温度、负荷电流、导线温度等因素作为覆冰增长的计算参量,建立了更加全面的覆冰增长模型。 (2)覆冰过程中,局部碰撞系数及碰撞区域随风速的提高快速增加,覆冰量及覆冰区域相应增大;环境温度及导线电流的增加使得溢流水产生,覆冰由雾凇改变为雨凇。 (3)与已有实验结果比较,得出本文预测覆冰形状略有误差,但覆冰总量差异很小,可以满足电力工程的需要。 [1] FARZANEH M. Atmosphere icing of power networks [M]. Berlin, Germany: Springer, 2008. [2] HUANG Xinbo, LIN Shufan. Ice growth prediction model of transmission lines based on Mamdani-type fuzzy neural network [C]∥Proceedings of the 15th International Workshop on Atmospheric Icing of Structures. Mount Pearl, Newfoundland, Canada: IWAIS, 2013: 59-71. [3] 王璋奇, 齐立忠, 杨文刚, 等. 集中质量法模拟覆冰在架空线脱冰动张力实验中的适用性研究 [J]. 中国电机工程学报, 2014, 34(12): 1982-1988. WANG Zhangqi, QI Lizhong, YANG Wengang, et al. Research on the applicability of lumped mass method for cable’s dynamic tension in the ice shedding experiment [J]. Proceedings of the CSEE, 2014, 34(12): 1982-1988. [4] MAKKONEN L. Modeling of ice accretion on wires [J]. Journal of Climate Applied Meteorology, 1984, 23(6): 929-939. [5] MAKKONEN L, STALLABRASS J R. Experiments on the cloud droplet collision efficiency of cylinders [J]. Journal of Climate Applied Meteorology, 1987, 26(10): 1406-1411. [6] 蒋兴良, 范松海, 胡建林, 等. 输电线路直流短路融冰的临界电流分析 [J]. 中国电机工程学报, 2010, 30(1): 111-116. JIANG Xingliang, FAN Songhai, HU Jianlin, et al. Analysis of critical ice-melting current for short-circuit DC transmission line [J]. Proceedings of the CSEE 2010, 30(1): 111-116. [7] 孙才新, 蒋兴良, 熊启新, 等. 导线覆冰及其干湿增长临界条件分析 [J]. 中国电机工程学报, 2003, 23(3): 141-145. SUN Caixin, JIANG Xingliang, XIONG Qixin, et al. Analysis of critical icing conditions of conductor and wet-dry grown [J]. Proceedings of the CSEE, 2003, 23(3): 141-145. [8] 黄新波, 欧阳丽莎. 输电线路覆冰关键影响因素分析 [J]. 高电压技术, 2011, 37(7): 1677-1682. HUANG Xinbo, OUYANG Lisha. Analysis on key influence factor of transmission line icing [J]. High Voltage Engineering, 2011, 37(7): 1677-1682. [9] 阳林, 郝艳捧. 架空输电线路覆冰状态评估模糊专家系统 [J]. 高电压技术, 2011, 37(12): 3028-3035. YANG Lin, HAO Yanpeng. Fuzzy expert system for condition assessment of overhead transmission line icing [J]. High Voltage Engineering, 2011, 37(12): 3028-3035. [10]戴栋, 黄筱婷, 代洲. 基于支持向量机的输电线路覆冰回归模型 [J]. 高电压技术, 2013, 39(11): 2822-2828. DAI Dong, HUANG Xiaoting, DAI Zhou. Regression model for transmission lines icing based on support vector machine [J]. High Voltage Engineering, 2013, 39(11): 2822-2828. [11]郝艳捧, 薛艺为, 杨林, 等. 复合绝缘子不同部位水滴撞击特性及其影响因素 [J]. 电网技术, 2014, 38(5): 1366-1372. HAO Yanpeng, XUE Yiwei, YANG Lin, et al. Characteristics of different parts of composite insulators impacted by water droplets and its influencing factors [J]. Power System Technology, 2014, 38(5): 1366-1372. [12]李学林, 姚涛. 特高压变电站支柱绝缘子重覆冰闪络仿真计算与试验分析 [J]. 高电压技术, 2013, 39(3): 612-617. LI Xuelin, YAO Tao. Study on flashover model of UHV substation post insulator in serious icing condition [J]. High Voltage Engineering, 2013, 39(3): 612-617. [13]FU P, FARZANEH M. Two-dimensional modelling of the ice accretion process on transmission line wires and conductors [J]. Cold Regions Science and Technology, 2006, 46(2): 132-146. [14]梁曦东, 李雨佳, 张轶博, 等. 输电导线的覆冰时变仿真模型 [J]. 高电压技术, 2014, 40(2): 336-343. LIANG Xidong, LI Yujia, ZHANG Yibo, et al. Time-dependent simulation model of ice accretion on transmission line [J]. High Voltage Engineering, 2014, 40(2): 336-343. [15]ZHANG Q, YANG Y. A new simpler rotation curvature correction method for Spalart-Allmaras turbulence model [J]. Chinese Journal of Aeronautics, 2013, 26(2): 326-333 [16]KIM J W. Ice accretion modeling using an Eulerian approach for droplet impingement [C]∥51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Reston, Virginia, USA: AIAA, 2013: 1-11. [17]ZSOLT P. Modeling and simulation of the ice melting process on a current-carrying conductor [D]. Quebec, Canada: Quebec University, 2006. [18]CANSDALE J T, MCNAUGHTON I I. Calculation of surface temperature and ice accretion rate in mixed water droplet ice crystal cloud [R]. Hampshire, UK: Royal Aircraft Establishment, 1977: 7-13. [19]HUNEAULT M, LANGHEIT C, CARON J. Combined models for glaze ice accretion and de-icing of current-carrying electrical conductors [J]. IEEE Transactions on Power Delivery, 2005, 20(2): 1611-1616. [本刊相关文献链接] 孙皖,牛璐,赖天伟,等.氮气在缩放喷管中非平衡自发凝结的数值研究.2015,49(4):130-133.[doi:10.7652/xjtuxb2015 04021] 曹文瑾,孙中国,席光.系泊型浮体运动的无网格法数值模型.2015,49(3):62-66.[doi:10.7652/xjtuxb201503011] 翟强,朱永生,闫柯,等.高速角接触轴承油气润滑两相流动特性数值研究.2014,48(6):86-90.[doi:10.7652/xjtuxb 201406015] 侯雨伸,王秀丽.气象过程信息挖掘与输电线路覆冰预测.2014,48(6):43-49.[doi:10.7652/xjtuxb201406008] 周磊,汪楚清,孙清,等.玻璃纤维增强复合材料输电塔节点承载力试验研究及有限元分析.2013,47(9):112-118.[doi:10.7652/xjtuxb201309019] 宋国兵,靳幸福,李德坤,等.识别模型参数的电压源换流器型直流输电线路纵联保护.2013,47(8):110-114.[doi:10.7652/xjtuxb201308019] 梁振锋,索南加乐,康小宁,等.利用最小二乘拟合算法的三相重合闸永久性故障判别.2013,47(6):85-89.[doi:10.7652/xjtuxb201306015] (编辑 赵炜 杜秀杰) Numerical Simulation for Icing and Influence on Transmission Line ZHU Yongcan1,HUANG Xinbo1,2,JIA Jianyuan1,TIAN Yi1,LIN Shufan2 (1. School of Electro-Mechanical Engineering, Xidian University, Xi’an 710071, China;2. School of Electronics and Information, Xi’an Polytechnic University, Xi’an 710048, China) The existing transmission line ice growth models only focus on the ice mass, it is difficult for them to predict ice morphology accurately. A computational model for local ice accretion on transmission lines is established in this study. Air dynamics equation is considered to solve parameters of the flow field around conductor, then Eulerian two-phase model is chosen to calculate droplet collision coefficient on the surface of iced conductor. Mass balance equation, including the parameters of droplet collision, water runback, evaporation and sublimation, is established, then icing heat balance equation is constructed. All unknown variables in the model are acquired by one-dimensional search under multiple hypothesis, and the freeze coefficient and ice mass of each unit are obtained. Eventually, the cases show that the local droplet collision coefficient and collision area increase with wind speed; rising temperature and conductor current leads to the water runback to transform rime ice type to glaze ice type. The obtained icing morphology and weight coincide well with the existing experimental results. transmission line; icing; numerical model; two-phase flow model; mass balance 2014-10-21。 朱永灿(1986—),男,博士生;黄新波(通信作者),男,教授,博士生导师。 国家重点基础研究发展计划资助项目(2009CB724507-3);国家自然科学基金资助项目(51177115);陕西省重点科技创新团队计划资助项目(2014KCT-16)。 10.7652/xjtuxb201507020 TM74 A 0253-987X(2015)07-0120-06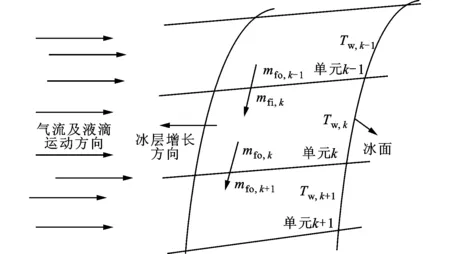
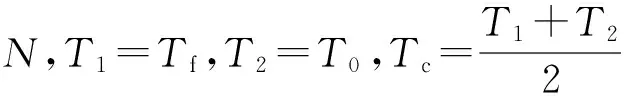
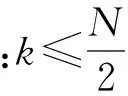
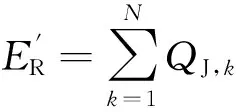
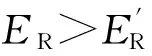
4 输电导线覆冰计算与分析

5 结 论

