采用随机矩阵的多扩展目标滤波器

韩玉兰,朱洪艳,韩崇昭

(西安交通大学电子与信息工程学院, 710049, 西安)



采用随机矩阵的多扩展目标滤波器

韩玉兰,朱洪艳,韩崇昭

(西安交通大学电子与信息工程学院, 710049, 西安)

针对杂波环境下多扩展目标的运动状态和形状信息的联合估计跟踪的问题,提出了一种基于随机矩阵的扩展目标跟踪算法。该算法采用具有噪声基于密度的空间聚类(DBSCAN)划分与预测划分相结合的联合划分算法对量测集进行划分,然后采用联合概率数据关联(JPDA)的软关联思想建立量测簇与扩展目标之间的对应关系,最后采用随机矩阵法对扩展目标进行估计获得运动状态和形状信息,特点是:将量测集划分为互不相交的几个簇,以使每个簇中的量测源于同一目标或杂波;建立量测簇与扩展目标之间的关联关系及状态更新。联合划分算法与DBSCAN划分的比较仿真实验表明,在有距离相近目标时采用联合划分算法比采用DBSCAN划分的滤波器的跟踪效果好得多。所提多扩展目标滤波器与ET-GMPDH滤波器的仿真实验表明,所提算法有较高的跟踪精度、较大的检测概率及较小的虚警概率。

滤波器;扩展目标;随机矩阵;跟踪算法

在传统的目标跟踪中,目标被当作点目标,即假设每个目标在每一时刻最多产生一个量测,这个假设只有当目标扩展相对传感器分辨率可以忽略时才成立。随着传感器精度的提高,每个目标在每一时刻可产生多个量测。例如,监测其他交通工具的车载雷达、安装在机器人上的激光测距传感器等可以在每一时刻产生多个量测,且量测个数会随着时间发生变化[1]。此时的跟踪问题被称为扩展目标跟踪。

近十几年以来,扩展目标跟踪问题受到了高度关注。Gilholm等假设扩展目标产生量测的个数服从Possion分布,假设量测源为某一空间分布,量测从此分布抽取产生[2]。但是,在实际应用中很难获取此分布。Koch将扩展目标形状近似为椭圆,将目标运动状态参数描述为Gaussian分布,将目标形状用服从逆Wishart分布的半正定随机矩阵描述,采用Bayesian递推的方法对目标运动状态和形状参数进行估计,这种方法被称为随机矩阵法[3]。Feldmann对随机矩阵法进行了改进,考虑了量测不确定性对目标形状估计的影响[4]。Baum提出采用随机超曲面模型(RHM)来描述量测源在物体表面的分布[5]。

上述方法主要是针对单扩展目标的跟踪方法。Wieneke将随机矩阵法与概率多假设跟踪(PMHT)相结合[6],Baum将随机超曲面模型与PMHT结合[7],实现了多扩展目标的跟踪,但是由于数据关联的计算量比点目标繁重得多,运算复杂度随着扩展目标个数及量测数急剧增加,所以限制了方法的应用范围。另一类多目标跟踪方法是基于随机有限集,Mahler将概率假设密度(PHD)滤波器推广到扩展目标和群目标跟踪中[8]。基于随机有限集的多扩展目标跟踪方法[8-12],递推地传递目标状态的分布信息,不需要数据关联即可从目标状态分布中同时提取多目标的个数和状态估计,避免了数据关联,但计算量大,不适合在线跟踪,而且不能给出航迹。

基于随机矩阵法的扩展目标跟踪,只提供了单个扩展目标的运动状态和形状信息。本文提出了基于随机矩阵法的多扩展目标在杂波环境下的跟踪方法。本文要解决的两个关键问题是:①将量测集划分为互不相交的几个簇,以使每个簇中的量测源于同一目标或杂波;②建立量测簇与扩展目标之间的关联关系及状态更新。本文提出将具有噪声基于密度的空间聚类(DBSCAN)[13]和预测划分相结合的联合划分策略,用以解决航迹起始和航迹维持阶段的量测集划分问题;利用联合概率数据关联(JPDA)[14]中软关联的思想描述目标与量测簇之间的关联关系,同时提出了多扩展目标航迹起始和航迹终止的方法。

1 问题描述

目标t的形状矩阵的演化可表示为[4]

(1)

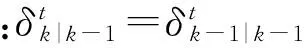
扩展目标的状态演化和量测模型服从[5]

(2)

(3)

(4)

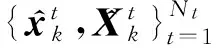
2 基于随机矩阵的多扩展目标跟踪

2.1 量测集划分

这里介绍DBSCAN和预测划分两种量测集划分方法,并通过对两种划分方法适用范围的分析,提出DBSCAN和预测划分相结合的联合划分策略。

DBSCAN划分采用DBSCAN聚类[15]思想对量测集进行划分。量测点的密度定义为:以量测点为中心、Eps为半径的邻域内的量测点(包括本身)个数。根据密度大小,将所有量测点分为核心点、边界点和噪声点。若量测点在半径Eps的邻域内含有超过NMinPts数目的量测点,则该点为核心点;若量测点密度小于NMinPts,但在某个核心点的Eps邻域内,则该点为边界点;既不是核心点也不是边界点的量测点称为噪声点。量测集的DBSCAN划分算法步骤可描述为:①删除噪声点;②距离小于Eps的所有核心点之间赋予一条边;③每组连通的核心点形成一个簇;④将边界点置于与之关联的核心点所在的簇中。

参数Eps和NMinPts可根据量测集的特性进行选择。对于源于扩展目标中的量测,距第n个最近邻(n不大于此扩展目标产生的量测数)点的距离较小;源于杂波的量测,距第n个最近邻距点的距离相对较大。可根据上述特性选择Eps参数的值:对于给定n,计算所有点的第n个最近邻的距离,并将其以递增排序;将第n个最近邻的距离急剧增加时的值作为Eps,选取n为NMinPts参数的值。

DBSCAN是基于量测距离的划分算法。当两个或多个扩展目标距离较近时,DBSCAN划分将源于不同目标的量测置于同一簇中,使量测集的划分结果出现较大的偏差,进而使状态和形状的估计都出现较大的误差。

(5)

式中:ε(p)是基于自由度d、概率p的累计χ2分布获得的阈值。如果有量测落入两个或多个簇中,将其划入距预测量测最近的簇中。

预测划分是基于模型的划分,划分效果与当前时刻的预测量测和预测形状矩阵有关,而预测量测和预测形状矩阵与前一时刻的估计量紧密相关。因此,当估计效果差时,如扩展目标初始化、航迹起始阶段、状态演化或量测模型建模与实际模型差别大时,不适合采用预测划分。需要指出的是:当目标机动性大、单一模型不能充分描述目标演化时,可以通过多模型对目标演化进行建模后,亦可采用预测划分。

通过上述分析,本文采用了DBSCAN和预测划分相结合的策略,该策略充分利用了DBSCAN和预测划分各自的优势。由于DBSCAN划分是基于量测集的距离进行划分,不需要可靠的预测信息,因此在预测信息可信度不高的航迹起始阶段采用DBSCAN划分。由于预测划分在两个或多个扩展目标相距较近的情况下也能够得到较理想的结果,因此在航迹维持阶段采用预测划分。

2.2 数据关联及状态更新

本节将JPDA软关联思想应用到多扩展目标跟踪问题中,并结合随机矩阵法对扩展目标的运动状态和形状矩阵进行估计。首先对每个扩展目标建立跟踪门,若跟踪门之间互不相交,或者相交区域中没有量测,则多扩展目标跟踪可简化为几个单扩展目标的跟踪。若有量测落入目标相关跟踪门的相交区域,引入可行事件,并根据可行事件的概率对每一种关联情况下的估计结果进行加权,最终获得运动状态、形状矩阵的估计结果。

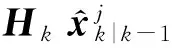
(6)

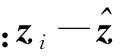
(7)

而κ可采用最优跟踪门限κ0[14],也可根据落入跟踪门的概率进行选择。

为表示量测簇与各目标跟踪门之间的关系,引入确认矩阵

(8)

确认矩阵生成后,可通过对确认矩阵进行拆分生成可行事件。可行事件的生成满足如下假设:每个簇有唯一的源,即最多对应一个扩展目标或杂波,每个扩展目标最多对应一个簇。对于给定的Nt个扩展目标和Nc个簇,一个可行事件

(9)

将可行事件的总个数记为Ne,并引入可行矩阵Γ(Ψi)来描述可行事件Ψi中的关联关系,即

(10)

为了方便讨论,引入每个可行事件Ψi的关联指示器υj(Ψi)和目标检测指示器λt(Ψi)

(11)

(12)

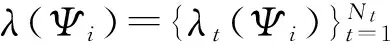
(13)

一旦Ψi给定,目标探测指示器λ(Ψi)和虚假量测数Fi就可以完全确定。因此,Ψi的先验概率可表示为

(14)

式中:μf(Fi)表示虚警量测数的先验概率质量函数,假设服从Poisson分布。

可行事件的多量测似然函数可表示为

(15)

若关联指示器υj(Ψi)>0,簇j源于目标tj的似然函数

(16)

若关联指示器υj(Ψi)=0,则

(17)

式中:Vg为跟踪门体积。

将式(14)、(15)代入Bayesian公式,可得可行事件的后验概率为

P(Ψi|Zk)=

(18)

式中:c为新的归一化常数。

量测簇j源于目标t的后验概率为簇j源于目标t的所有可行事件的后验概率的总和,即

(19)

(20)

目标状态和形状矩阵的估计结果步骤如下。

3 航迹起始与终止

3.1 航迹起始

扩展目标在每个时刻可以有多个量测值,因此不能直接采用点目标航迹起始方法。由式(3)、(4)描述的扩展目标量测及量测噪声模型,可将量测可解释为:由扩展目标质心产生量测,量测误差与扩展目标形状及传感器量测误差有关。因此,本文利用量测簇的量测均值及其协方差、采取类似点目标航迹起始的逻辑法,判断扩展目标的质心状态是否满足航迹起始的条件,对航迹进行确认。具体实现步骤如下。

(1)采用DBSCAN划分将量测集划分为几个簇,每个簇表示源于同一个目标的量测或噪声。

(2)计算每个簇的质心量测均值及其协方差。

(3)采用扩展目标逻辑法航迹起始的逻辑法对连续扫描期间(称为时间窗)的量测簇进行处理,以多重假设的方式通过预测和相关波门来识别可能存在的航迹。扩展目标逻辑法与点目标逻辑法的不同之处是:①点目标考虑的是时间窗内的量测,而扩展目标考虑的是时间窗内的量测簇;②在计算归一化距离、建立扩展目标质心量测的确认区域时,误差协方差采用质心量测的协方差。

(4)对于步骤(3)中确认为真实目标的航迹,采用随机矩阵法对航迹确认时间窗内的目标运动状态、形状矩阵进行估计。

3.2 航迹终止

本文采用跟踪门方法进行扩展目标航迹终止。其中,滤波残差及其协方差阵的计算与点目标不同,扩展目标的滤波残差向量为簇质心量测与预测量测之差,残差协方差由式(7)进行计算。若最优跟踪门限κ0[14]小于某一给定的最小门限值κmin,则航迹终止。

4 仿真结果

对监测区域[-3.5 km,20 km]×[-5 km,5 km]中的4个扩展目标进行跟踪。其中目标1、2、3起始于1 s,终止于100 s,目标4起始于11 s,终止于80 s。目标1、3约在36 s相遇,目标2、3约在43 s相遇,目标航迹如图1所示。每个扩展目标的形状均为主轴分别为30、10 m的椭圆。每个扩展目标每个时刻产生量测的个数服从均值为15的Poisson分布,杂波个数服从均值为10的Poisson分布。航迹初始化的时间窗长度为7 m。仿真结果是通过200次Monte Carlo仿真得到的。

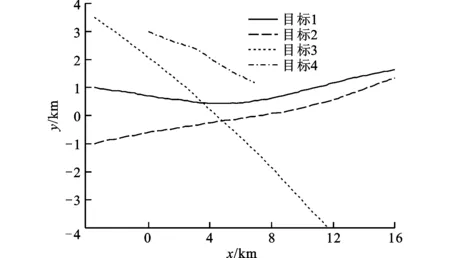
图1 扩展目标航迹

在不考虑航迹起始和终止算法、假设航迹已经起始、给定相应的初始化值的情况下,比较DBSCAN和预测划分对初始值的敏感程度,并与在已知正确关联情况下的跟踪结果进行比较。选取靠近各个量测簇边界的量测位置作为初始位置、真实形状矩阵的5倍作为初始预测形状矩阵。由图2、图3可得:由于DBSCAN划分结果只与量测集本身有关,因此初始值对基于DBSCAN划分的多扩展滤波器的影响很小,可根据较为准确的量测集划分得到较为可靠的目标运动状态和形状估计(除与目标相距较近的时刻外,其他时刻与在已知正确关联情况下的随机矩阵法跟踪结果几乎相同);预测划分是根据当前时刻扩展目标的预测运动状态和预测形状进行划分的,当初始值偏离真实值较大时,位置和形状估计的均方根误差趋于发散。因此,预测划分不适合用于估计量较差的航迹起始阶段。

图2 扩展目标位置估计的均方根误差

图3 扩展目标形状估计的均方根误差

图4 扩展目标位置估计的均方根误差

下面将航迹起始及航迹维持阶段都采用DBSCAN划分、联合划分策略,并与已知正确关联下的扩展目标跟踪结果进行比较。由图4、图5可以看出:在目标相距较远时,3种滤波方法得到的结果几乎相同;在目标相距较近时,基于DBCAN划分的扩展目标滤波器效果差,而基于联合划分策略的扩展目标滤波器的估计效果接近已知正确关联的滤波器的跟踪结果。这是由于:当目标相距较近时,扩展目标的量测之间没有明显界限,而DBSCAN划分是根据量测之间的距离进行划分的,其无法将距离较近的两个扩展目标的量测划分开,而将相距较近目标的量测置入到同一个簇中;联合划分在航迹维持阶段采用的是预测划分,预测划分是根据扩展目标的预测状态和预测形状进行的,与量测之间的距离关系不大,因此在目标相距较近时能获得较好的结果。

图5 扩展目标形状估计的均方根误差

这里通过将3种滤波器与文献[11]中的多扩展目标滤波器(ET-GMPHD-RM)进行比较,来验证航迹起始与终止算法的有效性,并进一步验证将JPDA软关联思想应用到多扩展目标的可行性。

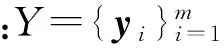
由图6可以得出:本文提出的航迹起始和终止算法能够较好地检测出目标的出现、终止,有较大的检测概率和较小的虚警概率(检测概率>0.986,虚警概率≤0.003 3)。在目标相距较近时,本文提出的滤波器处于航迹维持阶段,对扩展目标个数估计、检测概率没有出现较大的影响,而ET-GMPHD-RM滤波器却对扩展目标个数估计出现较大的偏差,检测概率也大大下降。

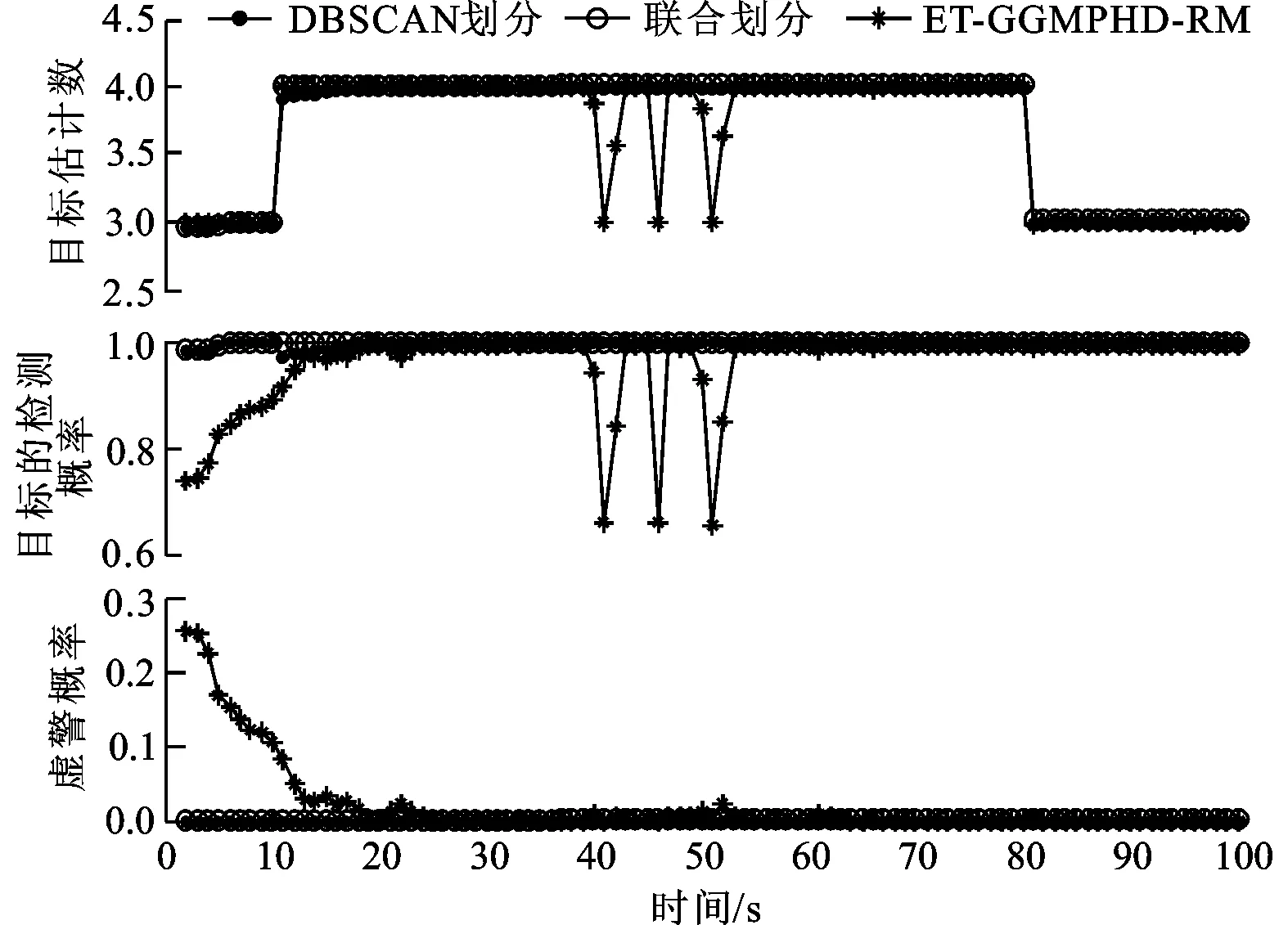
图6 3种滤波器的目标个数估计、检测概率和虚警概率

由图7可以得出:当目标距离较远时,基于随机矩阵、采用JPDA软关联的滤波器与ET-GMPHD-RM滤波器的位置和形状的均方根误差几乎相同;在扩展目标相距较近时,ET-GMPHD-RM滤波器的位置估计误差不大、形状误差较大,基于联合划分策略的滤波器的位置和形状估计误差都不大,基于DBSCAN划分的滤波器的位置和形状估计误差较大。

图7 滤波器的位置和形状估计的平均均方根误差

5 结 论

本文将JPDA关联思想推广到多扩展目标跟踪中,提出了一种基于随机矩阵法的多扩展目标滤波器。所提联合划分算法能够有效解决DBSCAN划分在有距离相近目标时的跟踪效果较差、预测划分对初始值敏感的问题,并为多目标扩展滤波器提出了航迹起始及终止算法。仿真结果验证了划分算法的使用范围、JPDA软关联的可靠性。仿真实验表明:在有距离相近目标时采用本文提出的联合划分算法比采用DBSCAN划分的滤波器的跟踪效果好;与ET-GMPDH-RM滤波器相比,本文提出的滤波器有较高的跟踪精度、较大的检测概率及较小的虚警概率。

[1] MICHAEL F, DIETRICH F, WOLFGANG K. Tracking of extended objects and group targets using random matrices [J]. IEEE Transactions on Signal Processing, 2011, 59(4): 1409-1420.

[2] GILHOLM K, SALMOND D. Spatial distribution model for tracking extended objects [J]. IEE Proceedings on Radar, Sonar and Navigation, 2005, 152(5): 364-371.

[3] KOCH J W. Bayesian approach to extended object and cluster tracking using random matrices [J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(3): 1042-1059.

[4] FELDMANN M, FRANKEN D, KOCH J W. Tracking of extended objects and group targets using random matrices [J]. IEEE Transactions on Signal Processing, 2011, 59(4): 1409-1420.

[5] BAUM M, HANEBECK U D. Random hypersurface models for extended object tracking [C]∥Proceedings of International Symposium on Signal Processing and Information Technology. Piscataway, NJ, USA: IEEE, 2009: 178-183.

[6] WIENEKE W, KOCH J W. Probabilistic tracking of multiple extended targets using random matrices [C]∥SPIE Proceedings: Vol 7698 Signal and Data Processing of Small Targets. Bellingham, WA, USA: SPIE, 2010: 769812.

[7] BAUM M, HANEBECK U D. Shape tracking of extended objects and group targets with star-convex RHMs [C]∥Proceedings of the International Conference on Information Fusion. Piscataway, NJ, USA: IEEE, 2011: 338-345.

[8] MAHLER R. PHD filters for nonstandard targets: I extended targets [C]∥Proceedings of the International Conference on Information Fusion. Piscataway, NJ, USA: IEEE, 2009: 915-921.

[9] ORGUNER U, LUNDQUIST C, GRANSTROM K. Extended target tracking with a cardinalized probability hypothesis density filter [C]∥Proceedings of the 14th International Conference on Information Fusion. Piscataway, NJ, USA: IEEE, 2011: 1-8.

[10]GRANSTROM K, LUNDQUIST C, ORGUNER U. Extended target tracking using a Gaussian mixture PHD filter [J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(4): 3268-3286.

[11]GRANSTROM K, ORGUNER U. A PHD filter for tracking multiple extended targets using random matrices [J]. IEEE Transactions on Signal Processing, 2012, 60(11): 5657-5671.

[12]HAN Yulan, ZHU Hongyan, HAN Chongzhao. A Gaussian-mixture PHD filter based on random hypersurface model for multiple extended targets [C]∥Proceedings of the International Conference on Information Fusion. Piscataway, NJ, USA: IEEE, 2013: 1752-1759.

[13]ESTER M, KRIEGEL H, SANDER J, et al. A density-based algorithm for discovering clusters in large spatial databases with noise [C]∥Proceedings of the International Conference on Knowledge Discovery and Data Mining. Menlo Park, CA, USA: AAAI, 1996: 226-231.

[14]韩崇昭, 朱洪艳, 段战胜, 等. 多源信息融合 [M]. 北京: 清华大学出版社, 2010.

[15]SCHUHMACHER D, VO B T, VO B N. A consistent metric for performance evaluation of multi-object filters [J]. IEEE Transactions on Signal Processing, 2008, 56(8): 3447-3457.

[本刊相关文献链接]

朱明,毛宽民.多通道测力仪动态信号反向滤波补偿方法.2015,49(2):117-123.[doi:10.7652/xjtuxb201502020]

闫小喜,韩崇昭,李威,等.拓展目标杂波概率假设密度估计.2015,49(1):92-96.[doi:10.7652/xjtuxb201501015]

任茂栋,梁晋,唐正宗,等.数字图像相关法中的优化插值滤波器.2014,48(7):65-70.[doi:10.7652/xjtuxb201407012]

吴彬,揭贵生,王恒利,等.无隔离三相逆变器两种直流分量抑制策略对比.2014,48(6):60-64.[doi:10.7652/xjtuxb 201406011]

韩玉兰,朱洪艳,韩崇昭,等.多扩展目标的高斯混合概率假设密度滤波器.2014,48(4):95-101.[doi:10.7652/xjtuxb 201404017]

包献文,卓放,谭佩喧.三相LCL型并网逆变器的模型分析及解耦控制.2014,48(2):44-49.[doi:10.7652/xjtuxb2014 02008]

胡克用,胥芳,艾青林,等.适用于光伏多峰功率跟踪的改进型粒子群优化算法.2015,49(4):140-148.[doi:10.7652/xjtuxb201504023]

(编辑 赵炜)

A Multi-Target Filter Based on Random Matrix

HAN Yulan,ZHU Hongyan,HAN Chongzhao

(School of Electronics and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

A multiple extended target filter based on random matrix is proposed to track the kinematic states and shape information of multiple targets in the presence of the clutter measurements. The proposed filter employs a joint partitioning algorithm, which combines the DBSCAN(density based spatial clustering of applications with noise) and the prediction partitioning algorithm, to partition the measurement set. Then, the JPDA(joint probabilistic data association), which is a soft association algorithm, is applied to description of the association between measurement clusters and extended targets. Finally, the method of random matrix is employed to estimate the kinematic states and shape information of extended targets. Simulation results which compare the joint partitioning algorithm with DBSCAN partitioning show that the filter by using joint partitioning algorithm could achieve much better tracking performance than that by using DBSCAN partitioning when there are spatially close extended targets. Moreover, simulation results in comparison with the ET-GMPHD filter show that the proposed multiple extended target filter has higher tracking accuracy, higher detection probability, and lower false alarm probability.

filter; extended target; random matrix; tracking algorithm

2014-12-27。

韩玉兰(1982—),女,博士生;朱洪艳(通信作者),女,副教授。

国家自然科学基金资助项目(61203220,61221063,61074176,61370037);国家“973计划”资助项目(2013CB329405)。

时间:2015-04-25

10.7652/xjtuxb201507017

TN274

A

0253-987X(2015)07-0098-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150425.1438.001.html