静止无功补偿器与发电机励磁系统的自适应鲁棒协调控制策略

张蕾,张爱民,景军锋,李鹏飞

(1.西安工程大学电子信息学院,710048,西安;2.西安交通大学电子与信息工程学院,710049,西安)



静止无功补偿器与发电机励磁系统的自适应鲁棒协调控制策略

张蕾1,张爱民2,景军锋1,李鹏飞1

(1.西安工程大学电子信息学院,710048,西安;2.西安交通大学电子与信息工程学院,710049,西安)

针对输电系统的暂态稳定性易受到不确定参数和未知扰动的影响,提出一种基于自适应逆推和L2增益控制的静止无功补偿器(SVC)与发电机励磁系统的自适应鲁棒协调(SVC-EARC)控制策略。采用递推法构造被控系统4个子系统的Lyapunov函数和能量函数,通过抵消不含扰动的项和含参数估计误差的项分别得到中间控制律和自适应律,使能量函数满足耗散不等式从而保证子系统稳定,递推至三阶子系统得到励磁控制律,结合将励磁系统和SVC系统进行动态互联的中间变量,最终完成SVC控制律的协调设计。仿真结果表明:SVC-EARC控制策略可将状态变量暂态轨线收敛时间缩短至2 s内,振荡幅值减少10%;自适应律能够有效地辨识不确定参数,有效提高了输电系统的暂态稳定性。

静止无功补偿器;自适应逆推;L2增益控制;协调控制

静止无功补偿器(SVC)具有实时调节无功功率的能力,能够改善电压质量、增强电气阻尼、提高电力系统的稳定性[1-2]。在电网结构和运行条件日益复杂的情况下,SVC调节系统和励磁控制系统之间的电气连接与交互影响不容忽略,通过SVC控制器与发电机励磁控制器的协调设计,可以有效缓解输电系统静态稳定性问题[3]。目前,限制电网传输容量的主要矛盾是输电系统的暂态稳定性,因此协调控制需对系统中的不确定因素进行分析和处理[4-5]。

为装设SVC的输电系统建立数学模型时,通常会做一些近似处理并假设参数已知,导致了未建模动态和不确定参数的存在[6-7],而系统在运行过程中遭受短路故障、切除故障负荷或发电机故障等大扰动时,将导致系统当前的网络结构与建模时有所不同[8]。此外,系统在运行时会随时遭受不确定扰动,如发电机轴上的扭矩干扰、励磁绕组上的电磁干扰以及负荷波动等,这些不确定性对系统的暂态稳定性的影响不容忽视[9-11]。

目前,为了提高装设SVC的输电系统的暂态稳定性,主要采用一些非线性协调控制方法,如基于无源性理论[12]、基于H∞理论[13]以及基于耗散系统理论[14]的鲁棒控制方法,基于逆推法和Terminal滑模面方法的自适应控制方法[15]等,前3种方法基于能量的角度分析了系统的耗散特性和鲁棒稳定性的联系,针对不确定扰动改善了系统的稳定性,最后一种方法采用逆推法对系统进行降阶,并通过滑模控制辨识参数,针对不确定参数提高系统稳定性。然而,以上这些方法并未同时考虑系统中的不确定参数和未知扰动,需要在协调控制中结合鲁棒控制方法和自适应控制方法提高系统暂态稳定性。

为了解决上述问题,本文提出一种基于自适应逆推和L2增益控制的SVC与发电机励磁的自适应鲁棒协调(SVC-EARC)控制策略,设计中兼顾控制系统的鲁棒性和参数自适应辨识能力。本文的协调控制策略包含了励磁控制律、SVC控制律以及参数自适应律的设计,并递推设计了系统的Lyapunov函数,用于证明系统的鲁棒稳定性。与现有方法相比,本文所提策略可以有效提高输电系统在不确定因素影响下的暂态稳定性。

1 系统数学建模和控制目标

被控对象是线路中点装设SVC的单机无穷大输电系统,假设发电机采用带有励磁控制的三阶非线性动态模型,不计调速器的作用,且SVC采用一阶惯性模型,则具有SVC与发电机励磁协调控制的系统数学模型可以表示为式(1)～式(4)[12-16]

(1)

式中:δ是发电机的功角;ω和ω0分别是发电机转子角速度及其稳态值。

(2)

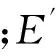
(3)

(4)

(5)

式中:x1、x2、x3和x4为系统的状态变量。

因此,由式(5)表示的本文的被控系统是包含不确定参数θ和不确定扰动w的非线性系统。本文研究的控制目标为通过自适应律的设计来辨识不确定参数θ,并通过励磁控制律uF和SVC控制律uL的协调设计来保证式(5)系统在遭受扰动的过渡过程中所有的状态变量一致有界,并能够快速收敛到平衡状态。

2 自适应鲁棒协调控制系统设计

2.1 算法描述

首先,将系统进行降阶,拆分成4个低阶子系统[17];然后,从最低阶子系统开始,采用逆推法构造子系统的Lyapunov备选函数(CLF),并构造扰动输入的能量函数,通过4个步骤依次对降阶子系统进行稳定性控制;最后,基于耗散系统理论,证明所设计的协调控制策略可以保证控制系统具有鲁棒扰动抑制的能力。

(6)

式中:σ1为正常数。

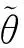
(7)

式中:ρ1为自适应增益;σ2为正常数。根据L2增益控制方法,选取扰动w1的能量存储函数为S1=V2。同时,构造下面的能量函数式

(8)

(9)

(10)

将式(9)、式(10)代入式(8)中,可整理为

(11)

第3步 针对由系统式(5)前3个微分方程所构成的三阶降阶子系统,将式(7)表示的CLF函数进行扩展,构造第3个CLF函数为

(12)

式中:σ3>0;ρ2>0为自适应增益。选取不确定扰动w1和w2的能量存储函数为S2=V3。同时,构造下面的能量函数

(13)

(14)

(15)

(16)

将式(14)～式(16)代入式(13)中,整理后可得

(17)

在第2步和第3步中都为不确定参数设计了自适应律,为了避免出现过参数化问题,设计第2个调节函数为

(18)

将式(12)表示的CLF函数进行扩展,构造第4个CLF函数为

(19)

式中:σ4>0。

选取不确定扰动w1、w2和w3的能量存储函数为S3=V4。同时,构造下面的能量函数

(20)

在这一步,将SVC控制律uL设计为

(21)

2.2 控制系统扰动抑制鲁棒性证明

(22)

由式(22)可知H3≤0,即

(23)

根据L2增益抑制理论,令能量存储函数V=2S3=2V4,能量供给率函数S=γ2‖w1‖2+γ2‖w2‖2+γ2‖w3‖2-‖y‖2,并将式(23)两边进行积分可得

(24)

由式(24)可知,在能量供给率函数为S和能量存储函数为V时,系统满足耗散性,由文献[1]中所述L2增益抑制理论可知,控制系统对于扰动w具有不大于γ的L2增益,证明所设计的协调控制策略可以保证控制系统具有L2增益下的鲁棒扰动抑制能力。

3 仿真结果与分析

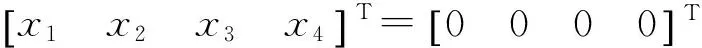
对以下情况进行仿真:系统初始工作在稳态,当t=0.2 s时,SVC所连母线右侧出口处发生三相短路,且在t=0.3 s时系统故障被切除,在这个过程中,将SVC-EARC控制方法与参考文献[15]中发电机励磁采用传统电力系统稳定器(PSS)加上自动电压调节器(AVR),SVC采用PI控制的常规分开(SVC-EDC)控制方法,在相同的初始条件下进行比较。

图1、图2为状态变量x1和x2在两种不同控制方法下的暂态响应轨线。x1和x2表示的是发电机的转子角和转子角速度的暂态响应特性,直接反映发电机功角的暂态性能。由图1可见,在SVC-EARC控制作用下,x1在1.5 s左右就收敛到稳态,而SVC-EDC则需要3.3 s左右,且第一摆振荡幅值减少30%左右。从图2可见,x2的响应速度在SVC-EARC控制方法作用下有大幅提高,振荡幅值减小,将扰动后的过渡过程缩减到0.5 s。

图1 状态变量x1的暂态响应曲线

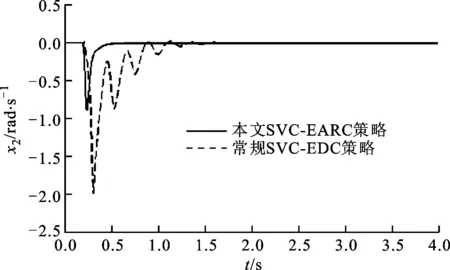
图2 状态变量x2的暂态响应曲线

图3和图4为状态变量x3和x4的暂态响应轨线。x3、x4分别对应于发电机的暂态电势和SVC投入系统的等效电纳的响应特性。由图3、图4可见,在SVC-EARC控制方法作用下,x3和x4的暂态轨线可以比SVC-EDC方法更快地收敛于故障前的稳定运行状态,分别将过渡过程时间缩短了1.5 s和2 s左右,且振荡幅值最高只有SVC-EDC方法的90%左右。

图3 状态变量x3的暂态响应曲线

图4 状态变量x4的暂态响应曲线

上述仿真结果也证明了在故障后状态变量是一致有界的,也验证了本文所提控制策略可以改善发电机功角、暂态电势和SVC等效电纳的暂态响应性能,从而提高系统的暂态稳定性。

图5为SVC-EARC控制作用下不确定参数的估计值响应特性。由图5可见,估计值只需1 s左右就可以迅速收敛到稳态值-0.17左右,与文中所设真值基本一致,所设计的自适应律能有效辨识不确定参数。

图5 自适应律辨识不确定参数响应曲线

4 结 论

本文提出了一种SVC与发电机励磁的自适应鲁棒协调控制方法。针对系统模型的不确定性和遭受的未知扰动,利用自适应逆推算法来设计系统励磁控制律和SVC控制律,并结合L2增益控制方法来抑制扰动,从而提高输电系统的暂态稳定性。系统仿真结果表明,本文所设计的自适应鲁棒协调控制策略与常规分开控制方法相比,在故障发生后的过渡过程中,状态变量能保证一致有界,收敛速度快,振荡幅值小,对于扰动具有较强的鲁棒性,且能有效地识别不确定参数。因此,有效提高了系统的暂态稳定性。

[1] 卢强, 梅生伟, 孙元章. 电力系统非线性控制 [M]. 北京: 清华大学出版社, 2008: 404-428.

[2]WIBOWORS,YORINON,EGHBALM.FACTSdevicesallocationwithcontrolcoordinationconsideringcongestionreliefandvoltagestability[J].IEEETransactionsonPowerSystem, 2011, 26(4): 2302-2310.

[3] 王颖博, 宁改娣, 王跃. 分布式静止同步串联补偿器抑制次同步谐振机理研究 [J]. 西安交通大学学报, 2011, 45(8): 102-107.WANGYingbo,NINGGaidi,WANGYue.Mechanismofdampingsub-synchronousresonancewithdistributedstaticsynchronousseriescompensator[J].JournalofXi’anJiaotongUniversity, 2011, 45(8): 102-107.

[4] SUN Liying, TONG Shaocheng, LIU Yi. Adaptive backstepping sliding mode H-infinity control of static var compensator [J]. IEEE Transactions on Control System Technology, 2011, 19(5): 1179-1185.

[5] SINGH R, SINGH A K. Transient stability improvement of a FSIG based grid connected wind farm with the help of a SVC and a STATCOM: a comparison [J]. International Journal of Computer and Electrical Engineering, 2012, 4(1): 55-60.

[6] ROBAK S. Robust SVC controller design and analysis for uncertain power systems [J]. Control Engineering Practice, 2009, 17(11): 1280-1290.

[7] MONDAL D, CHAKRABARTI A, SENGUPTA A. Optimal placement and parameter setting of SVC and TCSC using PSO to mitigate small signal stability problem [J]. International Journal of Electrical Power & Energy Systems, 2012, 42(1): 334-340.

[8] 辛焕海. 参数不确定性和饱和非线性对电力系统稳定影响的研究 [D]. 杭州: 浙江大学, 2007.

[9] MAHRAN A R, HOGG B W, ELSAYED M L. Co-ordinated control of synchronous generator excitation and static var compensator [J]. IEEE Transactions on Energy Conversion, 1992, 7(4): 615-621.

[10]何斌, 张秀彬, 赵兴勇. 多机系统中励磁与SVC的协调控制 [J]. 电工技术学报, 2008, 23(12): 152-159. HE Bin, ZHANG Xiubin, ZHAO Xingyong. Coordinated control of excitation and SVC in multi-machine power system [J]. Transactions of China Electrotechnical Society, 2008, 23(12): 152-159.

[11]RUAN Yingqin, WANG Jie. The coordinated control of SVC and excitation of generators in power systems with nonlinear loads [J]. Electrical Power and Energy Systems, 2005, 27(8): 550-555.

[12]HARIKRISHNA D, DHEKEKAR R S, SRIKANTHN V. A novel approach to dynamic stability enhancement using PID damped fuzzy susceptance controlled SVC [C]∥Proceedings of 2011 IEEE/PES Power Systems Conference and Exposition. Piscataway, NJ, USA: IEEE, 2011: 1-6.

[13]WANG Youyi, TAN Y K, GUO Guoxiao. Robust nonlinear coordinated generator excitation and SVC control for power systems [J]. International Journal of Electrical Power & Energy Systems, 2000, 22(3): 187-195.

[14]丁青青, 刘艳红, 汤洪海. 发电机和静止无功补偿器鲁棒非线性协调控制 [J]. 控制与决策, 2013, 28(7): 1099-1102. DING Qingqing, LIU Yanhong, TANG Honghai. Coordinated robust nonlinear control of synchronous generator and static var compensator [J]. Control and Decision, 2013, 28(7): 1099-1102.

[15]邹德虎, 王宝华. SVC与发电机励磁的逆推Terminal滑模协调控制 [J]. 电网技术, 2011, 35(4): 108-111. ZOU Dehu, WANG Baohua. Backstepping terminal sliding mode coordinated control for SVC and generator excitation [J]. Power System Technology, 2011, 35(4): 108-111.

[16]CONG L, WANG Y, HILL D J. Transient stability and voltage regulation enhancement via coordinated control of generator excitation and SVC [J]. Electrical Power and Energy Systems, 2005, 27(2): 121-130.

[17]MIROSLAV K, PETAR V K. Control Lyapunov functions for adaptive nonlinear stabilization [J]. Systems & Control Letters, 1995, 26(1): 17-24.

(编辑 刘杨)

A Coordinated Control Strategy with Adaptive Robustness for Static Var Compensators and Generator Excitation Systems

ZHANG Lei1,ZHANG Aimin2,JING Junfeng1,LI Pengfei1

(1. College of Electronics and Information, Xi’an Polytechnic University, Xi’an 710048, China;2. School of Electronics and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

An adaptive robust coordinated (ARC) control strategy for static var compensators (SVC) and generator excitation systems named SVC-EARC is proposed based on the adaptive backstepping andL2-gain control method to solve the problem that the transient stability of a transmission system is susceptible to uncertain parameters and unknown disturbances. The Lyapunov functions and energy functions are recursively constructed for four sub-systems of the controlled system. Intermediate control laws and adaptive laws are designed by offsetting the items without disturbances and the items with estimation errors to make the energy functions satisfy dissipation inequation, and to guarantee the stability of the sub-systems. An excitation control law is obtained through three steps. The coordinate design of the SVC control law is completed by combining the intermediate variable that connects the excitation system with the SVC system. Simulation results show that the SVC-EARC control strategy achieves the convergence of the states within 2 s, and reduces the oscillation amplitudes by 10%. It can be concluded that the adaptive law can effectively identify the uncertain parameter, and the transient stability of the system can be effectively improved.

static var compensator (SVC); adaptive backstepping;L2-gain control; coordinated control

2015-04-28。

张蕾(1981—),女,博士,讲师;张爱民(通信作者),女,教授,博士生导师。

国家自然科学基金资助项目(51177126);陕西省教育厅科研计划资助项目(14JK1306);西安工程大学学科建设经费资助项目(107090811);西安工程大学博士科研启动基金资助项目(BS1337)。

时间:2015-09-11

10.7652/xjtuxb201511016

TP273

A

0253-987X(2015)11-0096-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150911.1048.004.html