基于粒子群快速优化MP算法的多子波分解与重构
刘 霞,陈 晨,赵玉婷,汪 鑫
1.东北石油大学电气信息工程学院,黑龙江 大庆 163318 2.中国石油天然气集团公司大庆油田有限责任公司,黑龙江 大庆 163002
基于粒子群快速优化MP算法的多子波分解与重构
刘 霞1,陈 晨1,赵玉婷2,汪 鑫1
1.东北石油大学电气信息工程学院,黑龙江 大庆 163318 2.中国石油天然气集团公司大庆油田有限责任公司,黑龙江 大庆 163002
针对地震信号多子波分解与重构技术中匹配追踪算法能够根据地震信号自身特点进行自适应分解、但其计算量庞大的问题,笔者提出一种粒子群快速优化算法,用于快速搜索地震信号稀疏分解的最优匹配原子。即在迭代过程中,将搜索区域确定在高斯函数能量集中的部分,避免了搜索过程的“贪婪性”,能有效降低稀疏分解复杂度。同时,在粒子群算法中引入了一种多项式变异算子,可以有效避免搜索最优解的过度集中。实验结果证明,此算法将匹配追踪的分解精度提高了67倍,更使计算效率提高了153倍。
多子波;匹配追踪;粒子群
0 引言
地震信号是由不同能量、不同形状的地震子波叠加得到的,是复合谐波。常规的合成地震记录为一个单一的褶积模型,并不能真实反映地层的变化。多子波地震道模型则能更好地对地震信号进行描述。多子波分解与重构技术可以对地震信号进行分解,按照其频率、振幅、能量等属性的特点分解成一系列子波序列的集合,再针对得到的子波按照一定规则重新构建,用以描述地下的地层性质与地质构造。油气结构与非油气结构的地层对地震信号有着不同性质的响应,所以得到的子波在频率与能量上的表现也必定存在差异。那么,就可以依据已知的油气结构资料,将与油气结构变化相关的子波选择出来,筛除与油气结构变化不相关的子波,来重构成新的数据体。这样就能够得到与油气层变化最相关的地震道集合。多子波分解与重构技术已应用于薄层刻画、断层识别以及尖灭判别等领域[1-3]。因此,多子波分解与重构技术的研究有着重要的实际意义和应用价值。
目前应用较多的多子波分解与重构方法有小波变换、S变换和匹配追踪算法[2]等。匹配追踪算法(MP算法)近年来发展十分迅速。王纯伟等[3]对匹配追踪算法中原子库的构造进行了研究探讨,提出了采用非零相位的雷克子波来构建原子库的算法。张繁昌等[4]利用地震信号的局部特征作为先验信息点,采用动态搜索策略寻找最佳匹配原子。杨愚[5]则利用基于正交匹配追踪算法对信号进行稀疏分解,提高了收敛效果。
地震信号在过完备集上的最优稀疏分解是一个非确定多项式(non-deterministic polynomial,NP)问题。由Mallat和Zhang提出的匹配追踪算法就是一种从寻找全局最优解转化为在局部寻找次最优解的算法[6]。匹配追踪算法是一种贪婪算法,它的时频原子字典一定是冗余的,因此匹配追踪算法的精度很高,但同时这也就导致了在其运算过程中计算量庞大的问题。优化最佳匹配原子搜索算法能够有效降低计算复杂度。这也是本文的研究重点之一。
为了在保持精度的同时减少计算量,本算法在搜索最佳匹配原子时引入了粒子群优化算法[7]进行优化。同时在粒子群算法中引入一种多项式变异算子,避免搜索最优解的过度集中。将粒子群优化算法应用于匹配追踪算法中最佳匹配原子的搜索,使原子搜索速度加快、算法运行效率提高,是本文的核心研究内容。
1 多子波分解与重构技术
地震信号在地层中的传播形式复杂多样。目前最常用的合成地震记录是一个简单的褶积模型,即单一地震子波与地层反射系数序列的褶积,表达式为
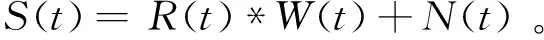
(1)
式中:R(t)表示地震反射系数序列;W(t)表示地震子波;N(t)表示噪音项。
这种常规的地震道模型便于使用,但它存在一定的局限性。因此,多子波分解与重构技术提出的多子波地震道模型能更好地对地震信号进行描述。
多子波地震道模型就是对地震道中不同时间的地震反射系数对应使用不同频率的子波,即一个与地震反射系数序列相对应的子波序列进行褶积,通过不断迭代拟合来表征地震数据,最终形成地震道。多子波地震道模型的表达式为
(2)
式中:i=1,2,…,M;Wi(t)表示第i层反射的地震子波;Ri(t)表示第i层的地震反射系数;N(t)表示噪音项。
多子波地震道分解的基本思想是基于多子波地震道模型,将地震道分解成不同形状、不同能量子波的组合。而重构的基本思想是通过对这些不同的子波分量进行分析,选取出符合重构要求的全部或部分子波,线性叠加得到一个新的地震道,从而得到一个新的数据体。
2 粒子群快速优化匹配追踪算法
2.1 MP算法基本原理
MP算法[8-11]是一种在局部寻找次最优稀疏分解的贪婪算法。定义H为Hilbert空间,D⊂H为过完备原子字典。设待分解信号为f,则f可以被分解为
(3)
且有
(4)
其中:Rmf为第m次迭代后剩余的残差信号;R0f=f;〈Rnf,gγn〉为Rnf与gγn的内积;gγn为第n次迭代匹配到的原子,满足
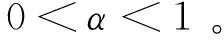
(5)
其中:G为参数集合;gγ为由参数γ定义的原子,且‖gγ‖=1。
MP算法的每次迭代总是在过完备原子字典D中寻找与残留信号Rmf内积绝对值相对较大的原子。
在MP算法中,过完备原子字典的构造是一个核心问题。这就要求在字典中原子数一定大于信号的长度,并且要与地震信号相匹配。鉴于Gabor原子具有比同类原子更好的时频聚集性,因此在本算法中过完备原子字典的构造采用Gabor原子来完成。
2.2 时频原子字典设计
Gabor原子字典是一个包含了Gabor基、δ函数和复正弦基的过完备原子字典[12-14]。Gabor原子是一种应用广泛的原子,其基本定义为
(6)
其中:t代表原子的时间值;γ=(s,u,v,w)是原子参数;s为尺度参数;u为位移参数;v为频率参数;w为相位参数。对参数进行离散化处理,先处理尺度参数,再根据得到的结果表示出位移参数、频率参数和相位参数。
原子参数的离散化表示为
(7)
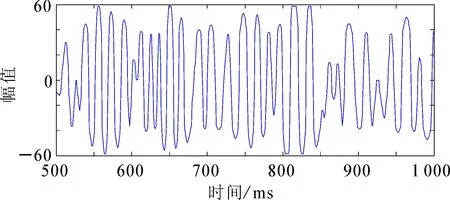
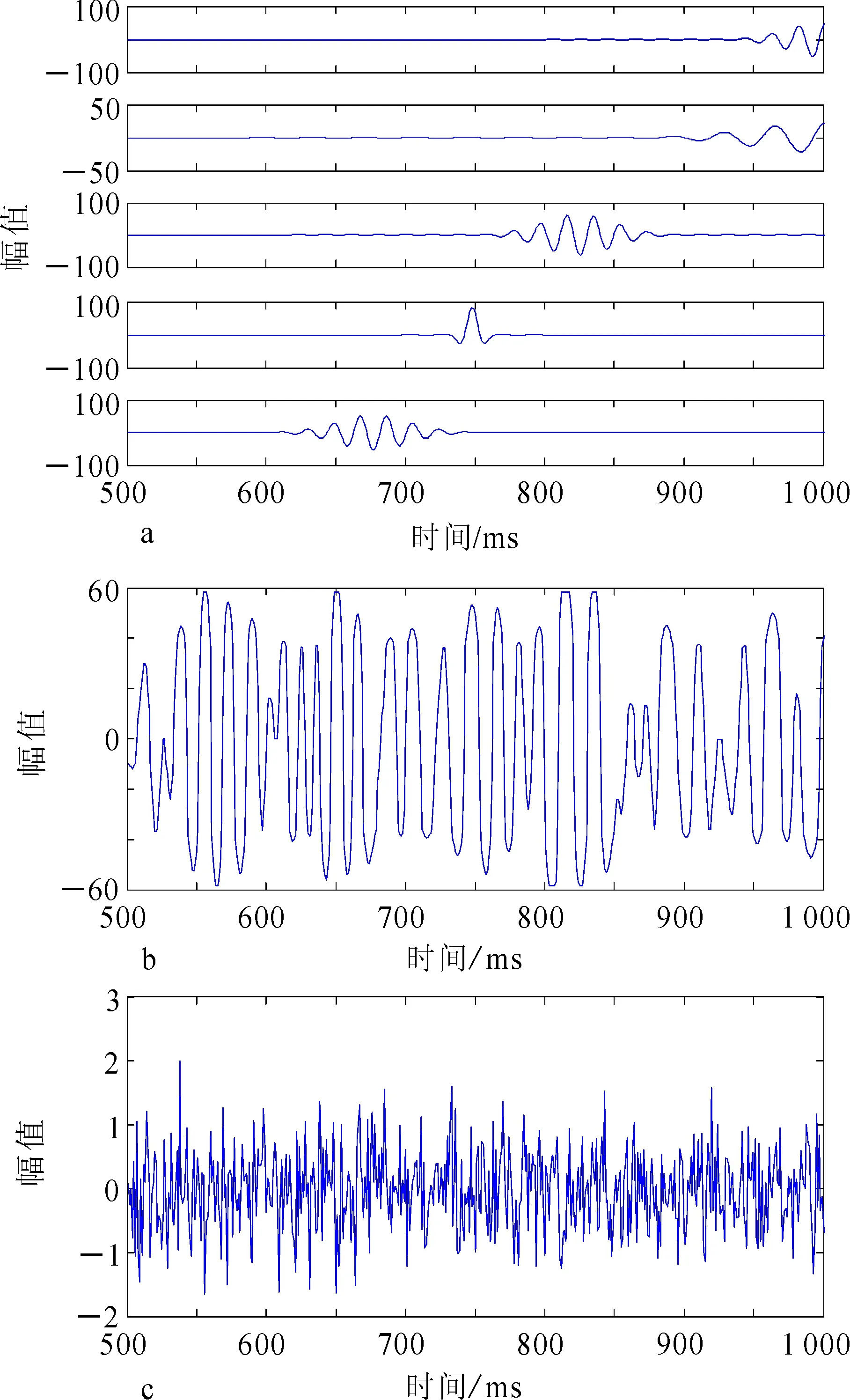
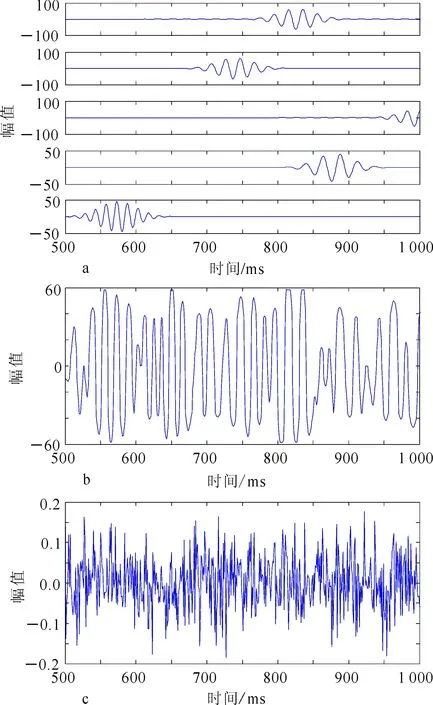
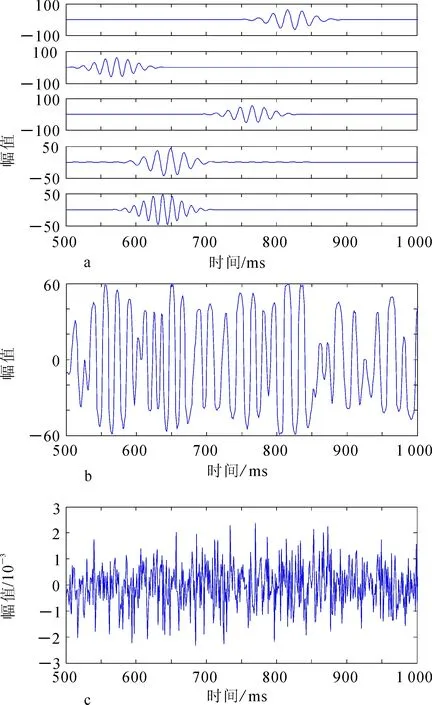
其中:a=2;Δu=1/2;Δv=π;Δw=π/6;0 原始的MP算法在搜索过程中需要遍历时频原子字典中的全部原子,因此搜索过程占用内存巨大。采用粒子群算法代替原始贪婪搜索算法,能够使搜索过程迅速收敛到最优解或次优解。参照原子参数的离散化表示,把原子参数s,u,v,w分别作为搜索空间中的一维,即本算法中的搜索空间为(s,u,v,w)所表示的四维空间。显然,这个四维参数空间能够产生的原子数是无穷多个的,Gabor原子字典只是根据规则对参数空间所代表的原子字典进行抽样选取的结果。因此,用粒子群算法搜索得到的原子能够达到细致刻画原始地震信号的效果。 2.3 改进的粒子群优化的MP算法 2.3.1 粒子群算法基本原理 粒子群优化算法(particle swarm optimization algorithm,PSO算法)首先在一个D维的搜索空间中初始化一个由n个粒子组成的种群X=(X1,X2,…,Xn),其中第i个粒子表示为一个D维的向量Xi=[xi1,xi2,…,xiD]T,代表第i个粒子在D维搜索空间中的位置[15]。该粒子的特征用位置、速度和适应度值表征。第i个粒子的速度为Vi=[Vi1,Vi2,…,ViD]T。通过计算适应度函数得到该粒子对应的适应度值,粒子的优劣即用其值的好坏表征。在本算法中,用信号或信号残差与原子内积的绝对值|〈Rmf,gγm〉|作为适应度函数,即可计算出每个粒子位置Xi对应的适应度值。 粒子在整个搜索空间中飞行,通过个体极值Pi和全局极值Pg的反馈及时更新个体位置;个体极值Pi是指粒子的飞行位置中适应度值最优位置,群体极值Pg是指种群中的所有粒子飞行过程中搜索到的适应度值最优位置。第i个粒子的个体极值为Pi=[Pi1,Pi2,…,PiD]T,种群的全局极值为Pg=[Pg1,Pg2,…,PgD]T。粒子每更新一次位置,适应度值也随之重新计算,通过比较粒子新的适应度值以及Pi、Pg的适应度值更新Pi和Pg位置。 在每一代的迭代过程中,粒子凭借个体极值与全局极值更新自身的速度、位置: (8) (9) 式中:ω为惯性权重;d=1,2,…,D;i=1,2,…,n;k为当前迭代次数;c1和c2为非负的常数,称为加速度因子;r1和r2为分布于[0,1]之间的随机数。为了避免粒子搜索的盲目性,通常将其位置、速度控制在一定的范围[-Xmax,Xmax]、[-Vmax,Vmax]。 2.3.2 快速搜索最优原子 在MP算法的迭代过程当中,为了搜寻到最佳匹配的原子,这种贪婪算法会将时频原子字典中所有的原子逐一搜索到位,因此,计算量之大是可以预见的。 2.3.3 种群变异算子 基本粒子群优化算法收敛速度快,具有相当强的通用性,但也有容易陷入早熟收敛、搜索精度不高、搜索后期迭代效率低等缺点存在。本算法在基本PSO算法中引入了变异操作,具体的多项式变异公式为 (10) (11) 其中:rk是在(0,1)之间均匀分布的随机数;ηm是变异分布指数。 此种变异操作不仅能使粒子跳脱出先前搜索到的最优位置,达到拓展种群搜索空间的目的,而且充分保持了种群的丰富性,为算法寻找到更优值提供了可能性。 2.4 算法实现流程 基于粒子群快速优化MP算法的多子波分解与重构具体实现步骤如下: 1)读取地震数据。 2)设定稀疏分解的基本参数,初始化重构信号与残差信号,并确定原子能量分布的范围。 3)搜索最佳匹配原子,在粒子群子程序中粒子位置及其速度采用实数编码,将信号或信号残差与原子内积的绝对值|〈Rmf,gγn〉|作为适应度函数。 4)初始化种群大小O、最大进化代数K和高斯函数能量集中部分的左右边界bleft,bright。计算粒子的初始适应度值,初始种群中每个粒子的目标函数是时频原子与信号或信号残差之间的内积。由于目标函数为求取最大值,适应度函数为求取最小值,则适应度函数等于目标函数绝对值的相反数。 5)将粒子的适应度值与Pi进行比较,如果优于Pi,则Pi被当前位置替换;如果所有粒子的Pi中有优于Pg的,则重新设置Pg。 6) 按公式(8)和(9)更新粒子的速度和位置,并进行变异操作,在普通粒子群算法的基础上引入变异算子。 7) 确定搜索时间域,将其限制在高斯函数能量集中的部分,并计算每一代新的适应度值,将得到的最优解进行个体极值与全局极值的更新。 8) 搜索得到的最优粒子即是每次迭代的最优原子参数,由此计算出最佳匹配原子gγn,再将该原子和信号或信号残差进行内积计算得到相应的原子系数。 9)利用选择的最优原子重构信号,如果达到最大迭代次数或最优解停滞不再发生变化,则终止迭代;否则将残差等参数返回到粒子群算法中继续搜索能够和残差达到最佳匹配的原子。 对地震信号进行稀疏分解后,按照表达式对信号进行重构,可以检测重构后得到的信息是否完整。重构信号信息的完整性可直接反应算法的准确性与可行性。 分别采用基本MP算法、基本粒子群优化的MP算法以及本文改进的粒子群快速优化MP算法对单道地震信号进行分解与重构。采用Gabor原子设计时频原子字典,种群大小为30,迭代次数为 1 000。图1为原始单道地震信号,图2为基本MP算法仿真结果,图3为基本粒子群优化的MP算法仿真结果,图4为粒子群快速优化的MP算法仿真结果。 图1 原始单道地震信号Fig.1 Original single channel seismic signal a.多子波分解(取前5个原子);b.多子波重构信号;c.多子波重构残差。图2 基本MP算法仿真结果Fig.2 Simulation results of basic MP algorithm a.多子波分解(取前5个原子);b.多子波重构信号;c.多子波重构残差。图3 基本粒子群优化的MP算法仿真结果Fig.3 Simulation results of MP algorithm optimized by the basic particle swarm a.多子波分解(取前5个原子);b.多子波重构信号;c多子波重构残差。图4 粒子群快速优化的MP算法仿真结果Fig.4 Simulation results of MP algorithm fast optimized by particle swarm 观察图2a、图3a、图4a不难发现,在搜索初期得到的原子包含更多的能量,信号的幅值与频率也与原信号较为接近,随着搜索过程的逐步深入,信号能量衰减迅速,后期搜索到的原子对整个原始信号的贡献也随之减小。通过对比可以看出,基本MP算法在搜索过程中的效率不高,甚至搜索到的前两个原子还有一定程度的能量损失,前5个原子的幅值均在[-100,100]的范围。基本粒子群优化的MP算法在一定程度上改善了原算法的不足,在第4个原子时就可以将幅值迅速收敛到[-50,50]的范围,但不可避免地在第3个原子处也出现了能量损失的现象。而粒子群快速优化的MP算法达到的效果最好,不但信号的收敛速度快,而且相较于其他两种算法,基本没有能量的损失。因此,在搜索过程中使用粒子群快速优化的算法,对于保持计算精度的同时提高计算速度是十分必要的。 基本粒子群优化算法与粒子群快速优化算法的仿真结果对比如图5所示。粒子群快速优化算法相比于基本算法,增加了快速搜索方法与种群变异操作。通过对比可以明显看出:基本算法在收敛过程中,适应度值的变化有相对平缓的阶段,其间下降速度略慢;而改进后的方法能使适应度值更快速地收敛到群体最优解,跳出局部极小值点,不易陷入局部最优,从而得到更优的结果。 图5 基本粒子群优化算法与粒子群快速优化算法仿真结果对比Fig.5 Comparison of simulation results of the basic particle swarm optimization algorithm and the particle swarm fast optimization algorithm 这3种算法在相同迭代次数的前提下,其重构残差幅值范围、内积计算次数以及运行速度对比结果如表1所示。设原始MP算法的运行速度为1,用倍数关系表示另两种方法的运行速度。 基本MP算法的重构残差幅值范围为[-2,2],基本粒子群优化的MP算法重构残差幅值范围为[-0.2,0.2],而本文提出的粒子群快速优化的MP算法重构残差幅值范围为[-3×10-3,3×10-3],计算精度得到了显著提高,基本上没有信号成分的损失。原始MP算法在信号分解中每次迭代需要搜索时频原子字典中全部原子,进行近似585 676次内积运算;在同等条件下,使用基本粒子群优化的MP算法在计算内积时需进行25 000次;而粒子群快速优化MP算法则只需进行8 330次。因此,在计算复杂度方面,基本粒子群优化算法比匹配追踪的贪婪算法至少下降23倍,而粒子群快速优化MP算法比原始的MP算法至少下降69倍。从表1可以直观地看出本文改进算法的运行速度得到了大幅提高。总的来看,基于粒子群快速优化的MP算法不但能够提升信号分解的效率,同时还可以得到良好的重构效果。 表1 算法比较 基于匹配追踪算法的多子波分解与重构技术,计算精度高,同时也存在着计算复杂度高的缺点。笔者将粒子群算法应用于匹配追踪算法中最佳匹配原子的搜索,极大地降低计算时的复杂度。对于粒子群算法易早熟的缺点,引入变异操作,保持了种群的多样性。同时针对时频原子字典冗余的问题,利用高斯函数的能量聚集性,快速确定搜索区域,将搜索的时间域限制在高斯函数能量集中的部分,能够有效缩小粒子搜索范围,在保持精度的前提下避免了匹配追踪算法的贪婪性。实验结果证明,该算法能够取得良好的重构效果。 [1] 邱娜. 地震子波分解与重构技术研究[D]. 青岛: 中国海洋大学, 2012. Qiu Na. Research on Seismic Wavelet Decomposition and Reconstruction Technology[D]. Qingdao: Ocean University of China, 2012. [2] 高静怀, 汪文秉, 朱光明, 等. 地震资料处理中小波函数选取研究[J]. 地球物理学报, 1996, 39(3): 392-400. Gao Jinghuai, Wang Wenbing, Zhu Guangming, et al. On the Choice of Wavelet Functions for Seismic Data Processing[J]. Chinese Journal of Geophysics, 1996, 39(3): 392-400. [3] 王纯伟, 杨胜利. 基于地震信号的匹配追踪算法[J]. 科技信息, 2010, 7: 443, 460. Wang Chunwei, Yang Shengli. Matching Pursuit Algorithm Based on Seismic Signal[J]. Science & Technology Information, 2010, 7: 443, 460. [4] 张繁昌, 李传辉. 基于正交时频原子的地震信号快速匹配追踪[J]. 地球物理学报, 2012, 55(1): 277-283. Zhang Fanchang, Li Chuanhui. Orthogonal Time-Frequency Atom Based on Fast Matching Pursuit for Seismic Signal[J]. Chinese Journal of Geophysics, 2012, 55(1): 277-283. [5] 杨愚. 利用粒子群算法实现信号 OMP 稀疏分解[J]. 微计算机信息, 2008, 24(3/4): 178-179, 201. Yang Yu. Signal Sparse Decomposition Based on OMP and PSO[J]. Microcomputer Information, 2008, 24(3/4): 178-179, 201. [6] 王春光, 刘金江, 孙即祥. 基于粒子群优化的稀疏分解最优匹配原子搜索算法[J]. 国防科技大学学报, 2008, 30(2): 83-87. Wang Chunguang, Liu Jinjiang, Sun Jixiang. Algorithm of Searching for the Best Matching Atoms Based on Particle Swarm Optimization in Sparse Decomposition[J]. Journal of National University of Defense Technology, 2008, 30(2): 83-87. [7] Zhou Xiaojun, Yang Chunhua, Gui Weihua, et al. A Particle Swarm Optimization Algorithm with Variable Random Functions and Mutation[J]. Acta Automatica Sinica, 2014, 40(7): 1339-1347. [8] 王国富, 张海如, 张法全, 等. 基于改进遗传算法的正交匹配追踪信号重建方法[J]. 系统工程与电子技术, 2011, 33(5): 974-977. Wang Guofu, Zhang Hairu, Zhang Faquan, et al. Orthogonal Matching Pursuit Signal Reconstruction Based on Improved Genetic Algorithm[J]. Systems Engineering and Electronics, 2011, 33(5): 974-977. [9] Huggins P S, Zucker S W. Greedy Basis Pursuit Signal Processing[J]. IEEE Transactions, 2007, 55(7): 3760-3772. [10] Kim S J, Koh K, Lustig M, et al. An Interior-Point Method for Large-Scale-Regularized Lease Squares[J]. IEEE Journal of Selected Topics in Signal Processing, 2007, 1(4): 606-617. [11] 邵君, 尹忠科, 王建英. 基于FFT的MP信号稀疏分解算法的改进[J]. 西南交通大学学报, 2006, 41(4): 466-470. Shao Jun, Yin Zhongke, Wang Jianying. Improved FFT-Based MP Algorithm for Signal Sparse Decomposition[J]. Journal of Southwest Jiaotong University, 2006, 41(4): 466-470. [12] 王纯伟. MP算法在地震信号去噪中的应用研究[D]. 成都: 西南交通大学, 2010. Wang Chunwei. The Application Research of Matching Pursuit in Seismic Signal Denoising[D]. Chengdu: Southwest Jiaotong University, 2010. [13] 王成梅. 地震信号稀疏分解快速算法及原子库选择研究[D]. 成都: 西南交通大学, 2010. Wang Chengmei. The Research on Fast Algorithm of Seismic Signal Sparse Decomposition and Atomic Dictionary Selection[D]. Chengdu: Southwest Jiaotong University, 2010. [14] Wang Yanghua. Multichannel Matching Pursuit for Seismic Trace Decomposition[J]. Geophysics, 2010, 75(4): 61-66. [15] 杜润林, 刘展. 基于粒子群优化的细胞神经网络油气重力异常信息提取[J]. 吉林大学学报:地球科学版, 2015, 45(3): 926-933. Du Runlin, Liu Zhan. Gravity Anomaly Extraction for Hydrocarbon Based on Particle Swarm Optimization and Cellular Neural Networks[J]. Journal of Jilin University: Earth Science Edition, 2015, 45(3): 926-933. Multi-Wavelet Decomposition and Reconstruction Based on Matching Pursuit Algorithm Fast Optimized by Particle Swarm Liu Xia1, Chen Chen1, Zhao Yuting2, Wang Xin1 1.SchoolofElectricalEngineeringandInformation,NortheastPetroleumUniversity,Daqing163318,Heilongjiang,China2.DaqingOilfield,ChinaNationalPetroleumCorporation,Daqing163002,Heilongjiang,China In a multi-wavelet decomposition and reconstruction of seismic signal, the matching pursuit algorithm can be adaptive according to the characteristics of the seismic signal itself. In view of the large amount of calculation, the author presents a particle swarm fast optimization algorithm, which is used for fast search optimum matching atoms of seismic signal sparse decomposition. In concrete, the searching area is determined by the energy concentrated part of Gaussian function in the process of iteration. This can avoid the greediness during the searching process, and effectively reduce the sparse decomposition complexity. At the same time, a polynomial mutation operator is introduced in the particle swarm optimization algorithm, which can effectively avoid the excessive concentration during searching the optimal solution. The experimental results show that the algorithm can reach a precision of matching pursuit decomposition 67 times higher than before, and increase the calculation efficiency by 153 times. multi-wavelet; matching pursuit; particle swarm optimization 10.13278/j.cnki.jjuese.201506303. 2015-01-05 黑龙江省自然科学基金项目(F201404) 刘霞(1970--),女,教授,博士,主要从事信号处理、鲁棒滤波、模型降阶、网络控制系统等研究,E-mail:liu-xia2k@163.com。 10.13278/j.cnki.jjuese.201506303 P631.4 A 刘霞,陈晨,赵玉婷,等. 基于粒子群快速优化MP算法的多子波分解与重构.吉林大学学报:地球科学版,2015,45(6):1855-1861. Liu Xia, Chen Chen, Zhao Yuting, et al. Multi-Wavelet Decomposition and Reconstruction Based on Matching Pursuit Algorithm Fast Optimized by Particle Swarm.Journal of Jilin University:Earth Science Edition,2015,45(6):1855-1861.doi:10.13278/j.cnki.jjuese.201506303.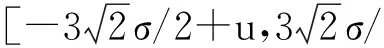
3 子波分解与重构仿真测试及结果分析


4 结语

