ADS－B 系统运行可靠性评价方法

胡水镜

(中国民航飞行学院 空管中心，四川 广汉 618307)

广播式自动相关监视系统(Automatic Dependent Surveillance－Broadcast，ADS－B)是基于全球卫星定位系统，利用地空/空空数据通信，实现空地飞机实时跟踪定位和相互感知，达到自动监控和预警，避免飞机危险接近的一种新型航行监视系统。目前，随着ADS－B 系统在我国空中交通管制中的广泛应用，提高系统运行可靠性已迫在眉捷，而可靠性评价结果是确定设备选型、维护策略以及维护资源投入等提高可靠性的决策依据，因此，建立客观实用的ADS－B 系统运行可靠性评价模型非常重要。

ADS－B 是由导航数据定位系统、机载设备以及地面接收处理显示设备组成的复杂系统，可靠性水平需要通过具体的评价指标体现，采用适当的评价方法进行综合反映，然而ADS－B 系统作为一种新兴技术，针对其可靠性评价指标和评价方法，尚未发现相关研究文献［1 ～4］。目前，复杂系统的可靠性评价方法主要有加权综合评价法、模糊综合评价法以及神经网络法等，但这些方法分别存在反映信息不全面，计算繁锁、人为因素影响大，样本数据量大以及计算不稳定易局部收敛等缺点［5－7］。

鉴于此，本文提出将T－S 模糊系统与神经网络有机结合的模糊神经网络应用于ADS－B 系统运行可靠性评价。利用T－S 模糊系统将可靠性评价指标和主观信息相结合，建立单项评价指标到综合评价的非线性映射关系，通过神经网络的自适应训练，调整模糊规则和隶属度函数，构造一种T－S 模糊神经网络，实现模糊系统与神经网络的优势互补。

1 可靠性评价指标

ADS－B 系统运行可靠性是指在规定的工作条件下和规定的时间内保持无故障运行的能力。依据ADS－B 系统运行特点和实际情况，运行可靠性的评价指标确定为:

(1)平均首次故障时间MTTFF。首次故障时间是ADS－B 系统投入使用至首次发生故障的持续运行时间。平均首次故障时间MTTFF 的计算公式为

式中，ti为i 第套ADS－B 系统的首次故障时间;n 为样本容量即被观察的ADS－B 系统数量。

(2)平均故障间隔时间MTBF。平均故障间隔时间是指ADS－B 系统发生故障后，经维修仍能正常工作，两次相邻故障间隔的平均运行时间，具体计算公式为

(3)平均维修时间MTTR。ADS－B 系统维修时间包括预防维修时间、维修准备时间和修复性维修时间，其平均值称为平均维修时间MTTR，具体计算公式为

式中，ti为第i 套ADS－B 系统的总维修时间;n 为被观察的ADS－B 系统数量;N 总维修次数。

(4)平均可用度A。平均可用度是对ADS－B 系统可靠度与维修度综合起来的一个评价指标，它表示ADS－B 系统在规定的工作条件下，在任意时刻正常工作的概率，具体计算公式为

式中，TD为平均维修等待时间，该时间主要与厂家服务、备件供应以及维修管理等因素相关。

(5)维修时间率RRT。

根据ADS－B 系统在我国的实际运行情况，用上述5 项评价指标建立运行可靠性评价标准，如表1所示。

表1 可靠性评价标准

2 可靠性评价模型建立

以表1 中的ADS－B 系统运行可靠性的5 项评价指标MTTFF、MTBF、MTTR、A 以及RRT 作为输入向量，将可靠性综合评价作为输出向量，建立n 维输入单输出的T－S 模糊神经网络。

2.1 T－S 模糊系统

T－S 模糊系统使用“if－then”规则形式来定义，在规则为Ri的情况下，模糊推理如下式中，Ri为第i 条模糊规则;xj为模糊变量;为模糊系统的模糊集;为模糊系统参数;yi为根据模糊规则得到的输出。输入部分是前提或前件，其值是模糊的;输出部分是结论或后件，其值是确定的，该模糊推理表示输出为输入的线性组合。

假设输入向量x=［x1，x2，…，xk］，根据模糊规则计算各输入向量xj的隶属度函数

计算模糊系统的输出值

2.2 T－S 模糊神经网络结构

T－S 模糊神经网络结构如图1 所示，由前件网络和后件网络两部分组成，前件网络匹配模糊规则的前提，后件网络生成模糊规则的结论［8］。

(1)前件网络。前件网络分为4 层。第1 层为输入层，其与输入向量x=［x1，x2，…，xk］连接，节点数与输入向量的维数相同;第2 层为模糊化层，每个节点代表一个模糊变量值，利用隶属度函数式(6)对输入向量进行模糊化，计算得出模糊隶属度值第3 层为模糊推理层，每个节点代表一个模糊规则，利用模糊连乘式(7)，计算得出模糊规则的适应度;第4 层为去模糊化层，节点数与第3 层相同，对模糊规则的适应度进行归一化计算。

(2)后件网络。后件网络分为3 层。第1 层为输入层，节点数比输入向量的维数多1，其中第1 个节点的输入值固定为1，以提供模糊规则后件中的常数项;第2 层为后件计算层，每个节点代表一个规则，节点数与前件网络中的第3、4 层相同，后件计算:第3 层为输出层，利用后件和适应度归一化计算结果，按照式(8)进行计算，得出输出值。

图1 T－S 模糊神经网络结构

2.3 T－S 模糊神经网络的学习算法

(1)误差计算

式中，yd为期望输出;yc为网络输出;e 为期望输出和网络输出的误差。

(2)参数修正计算

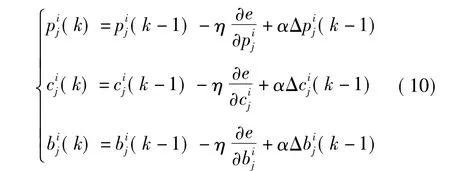
式中，η 为学习率;α 为动量因子。

3 实验仿真与应用

3.1 数据准备

根据表1 中的可靠性评价标准，按随机均匀分布方式内插生成训练样本的输入向量148 组，其中优1 组，良49 组，中49 组，次49 组。设表征可靠性水平优、良、中、次和差的数值区间为( －∞，1］、(1，2］、(2，3］、(3，4］和(4，∞)，按上述相同方式生成训练样本对应的输出向量148 组。检验样本采用与生成训练样本相同的方法生成13 个样本。

3.2 网络训练

根据ADS－B 系统运行可靠性评价的输入和输出向量维数，确定网络的输入节点数为5，输出节点数为1，设定隶属度函数为20 个，所以本文中T－S 模糊神经网络结构为5－20－1，其算法流程如图2 所示。

图2 T－S 模糊神经网络算法流程

在Matlab R2010a 中编写计算程序，初始的模糊系统参数p0～p5和隶属度函数中心c 和宽度b 随机生成，学习率设为0.001，动量因子设为0.02，将148 组训练数据载入T－S 模糊神经网络，训练200 次后输出结果如图3 所示。由图3 可以看出，网络输出和期望输出较为接近，网络训练的误差区间为［－0.018 9，0.043 2］，该误差对ADS－B 系统运行可靠性定性评价没有影响，能够满足实际评价要求。

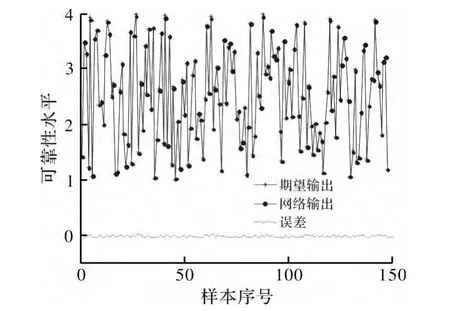
图3 T－S 模糊神经网络训练曲线

3.3 验证与分析

将13 组检验样本数据输入已训练好的T－S 模糊神经网络，进行ADS－B 系统运行可靠性评价，结果如表2 所示。

表2 检验样本的评价结果

据表2 可得出，利用T－S 模糊神经网络对ADSB 系统运行可靠性进行评价，绝对误差的最大值为0.019 8，最小值为0.003 9，相对误差均在2%以内，具有较高的精确性和良好的泛化能力，其评价结果准确可靠。若能在可靠性评价水平优和差两个等级中增加更多的将训练样本，T－S 模糊神经网络的稳定性和泛化能力将进一步提高，评价结果将更加准确可靠。

3.4 可靠性评价应用

根据某飞行训练单位5 套ADS－B 系统运行可靠性各评价指标的实际值，利用已训练好的T－S 模糊神经网络进行可靠性的综合评价，结果如表3 所示。

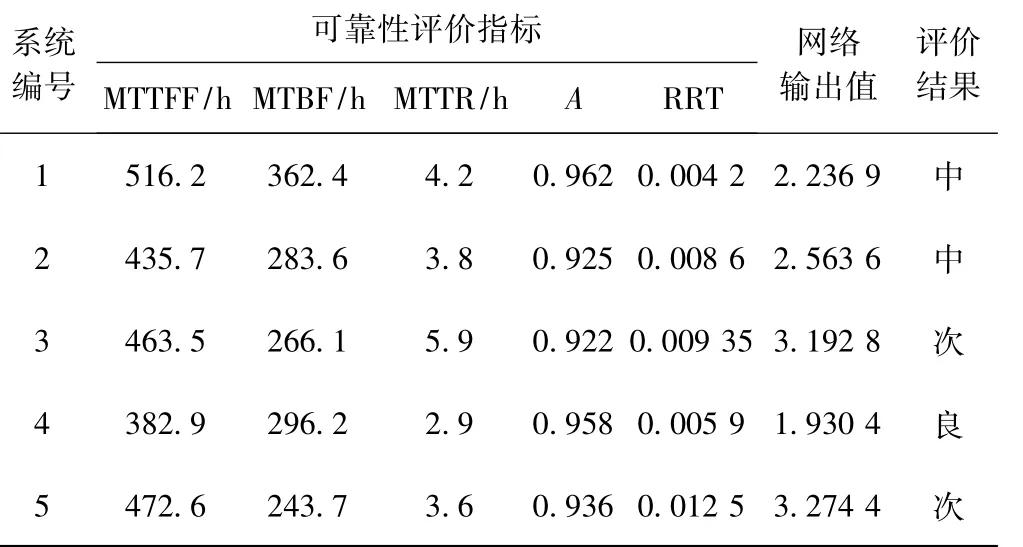
表3 可靠性评价结果

据表3 可看出，3 号和5 号ADS－B 系统运行可靠性较差，应改进相应维护策略和增加维护资源投入，以提高运行综合可靠性水平。

4 结束语

基于ADS－B 系统运行特点和实际情况，确定平均首次故障时间、平均故障间隔时间、平均维修时间、平均可用度和维修时间率为运行可靠性的评价指标，并建立相应的可靠性评价标准。以5 项可靠性评价指标为输入向量，利用T－S 模糊系统构建可靠性综合评价的非线性映射关系，经神经网络的自适应训练，调整模糊规则和隶属度函数，建立了一种基于T－S 模糊神经网络的ADS－B 系统运行可靠性的综合评价方法。该方法可解决加权综合评价法、模糊综合评价法以及神经网络法所存在的缺点。实验仿真与应用情况表明，该方法可行、有效，具有较高的计算稳定性、精确性和良好的泛化能力，评价结果客观、准确可靠，可作为提高ADS－B 系统运行可靠性的决策参考。

［1］ 倪育德，刘萍，马宇申.基于ADS－B 意图信息的航迹预测改进算法［J］.电讯技术，2014，54(2):156－162.

［2］ 周雷，辛晓娜，陈川波.结合ADS－B 的航管监视数据融合关键技术［J］.计算机工程与应用，2013，49(14):231－235.

［3］ 张兴旺.ADS－B 系统的故障模式、影响及危害度分析(FMECA)［J］.科 学 技 术 与 工 程，2013，13(29):8846－8850.

［4］ 张青竹，张军，刘伟，等.民航空管应用ADS－B 的关键问题分析［J］.电子技术应用，2007(8):72－74.

［5］ 刘晶郁，李雪莉，肖金坚，等.基于综合评判法的客车可靠性评价［J］.汽车技术，2013(1):9－11.

［6］ 张晓南，刘安心，曾凡勇，等.模糊综合评判法在军用工程机械可靠性与维修性评价中的应用［J］.矿山机械，2010，38(8):42－45.

［7］ 张宏斌，贾志新，郗安民，等.DK77 系列电火花线切割机床可靠性评价模型［J］.制造技术与机床，2010(4):88－91.

［8］ 孔增圻，徐红兵.基于T－S 模型的模糊神经网络［J］.清华大学学报:自然科学版，1997，37(3):76－80.