我国鸡蛋价格趋势周期分解和冲击效应分析
汪武静,吕官旺,石自忠
(1中国农业科学院农业经济与发展研究所,北京 100081;2内蒙古丰镇市农业局,内蒙古丰镇 012100;3中国农业大学经济管理学院,北京 100083)
作为畜牧业养殖领域内重要的产品,鸡蛋产业对于促进我国畜牧业快速发展有非常重要的意义。鸡蛋价格时涨时跌的波动日益成为社会关注的焦点,关系着消费者的生活质量,也制约着家禽产业的快速发展。从长期来看,鸡蛋价格究竟如何进行周期波动,相关因素对鸡蛋价格波动究竟贡献了多大份额是重要的问题。定量地把握鸡蛋价格波动趋势周期,较为准确地评价影响鸡蛋价格波动的因素,更好地把握鸡蛋价格波动规律,对保障中国禽蛋产业稳步发展、缓解鸡蛋价格频繁波动、促进畜牧业经济合理有序的发展具有重要意义。
从国内研究动态来看,运用计量经济学研究鸡蛋价格波动的研究主要集中在鸡蛋价格的市场传导机制、鸡蛋市场价格的短期预测和鸡蛋价格的波动成因分析。李哲敏等[1]运用协整检验,向量误差修正模型(VEC)分析了蛋鸡产业链中的价格传导关系;刘明月等[2]运用成分分解法对新疆鸡蛋价格进行数据分解,运用VAR 模型分析价格随机成分变动对鸡蛋价格冲击效应;谭银清等[3]研究表明,我国鸡蛋价格波动存在明显的季节性、周期性和趋势性,并且运用向量自回归模型(VAR)实证了玉米价格、商品代蛋雏鸡价格和CPI 波动对鸡蛋价格波动有更大影响且持续时间更长。就鸡蛋价格波动趋势周期分解来说,大部分成果都是利用HP 滤波进行分析,例如黄体冉等[4]运用HP 滤波等方法对北京市鸡蛋批发市场价格进行了分析。但HP 滤波分析方法在进行趋势周期分解时,需要假设趋势周期成分具有充分的平滑性,且直接滤出序列的短期成分,使得周期成分中包含随机趋势,从而分解的结果可能与周期定义不一致,Beveridge-Nelson 分解法(B-N 分解法)改进了这一缺陷。已有大部分文献采用B-N 分解法来研究猪肉、牛肉价格波动趋势周期分解[5,6],还没有文献利用B-N 分解法来更准确地研究鸡蛋价格波动趋势周期。在已有文献研究的基础上,本文主要采用B-N 分解法对鸡蛋价格进行趋势周期分解,并运用VAR 模型中的方差分解定量研究影响鸡蛋价格变动的各个因素,同时采用方差统计比,计算随机冲击对于鸡蛋价格波动的影响程度。
1 研究方法与数据说明
1.1 研究方法
为分析我国鸡蛋市场价格波动情况,以及鸡蛋价格和商品代蛋雏鸡价格、蛋鸡配合饲料价格之间的定量关系,本研究利用Beveridge-Nelson 分解法、VAR 模型和方差统计比公式。首先对鸡蛋价格进行趋势周期分解,分析确定性趋势和随机趋势,并划分价格波动的周期性,再利用脉冲响应函数和方差分解来定量研究商品代蛋雏鸡价格、蛋鸡配合饲料价格波动的贡献份额。最后在方差分解的基础上,利用Cochrane (1988)提出方差比统计量,计算鸡蛋价格随机冲击对鸡蛋价格变化的贡献份额。Beveridge-Nelson 分解法见本课题的研究成果[5]一文。方差统计比的方法需要一些研究基础,在后文有详细说明。由于篇幅限制,本文不再对研究方法详细描述。本文运算数据采用软件Stata 12.0 和Eviews 6.0。
1.2 数据来源
本文研究所使用的价格数据来源于中国畜牧业信息网(网址:http://www.caaa.cn/),价格序列包括鸡蛋市场价格(EP)、鸡蛋配合饲料价格(CP)、商品代蛋雏鸡价格(MP)。序列区间为2000 年1 月—2014 年12月,鸡蛋价格的序列如图1。进行分析时,以2000 年1月为基期,用定基CPI 指数对原序列进行平减,然后对平减后的序列分别取对数,同时对序列进行季节调整,得到新的序列分别记为LNEP (鸡蛋价格)、LNCP (蛋鸡配合饲料价格)、LNMP (商品代蛋雏鸡价格)。从图1 价格走势图可以看出,鸡蛋价格数据很可能是非平稳的时间序列,因此需要对其进行差分。图1 从其波动趋势大致可以看出,可能是平稳时间序列,在下文将会进行平稳性检验。

图1 鸡蛋价格和鸡蛋价格的一阶差分
2 鸡蛋价格趋势周期分析
2.1 序列平稳性检验
本文利用ADF 检验对所使用的价格序列及其一阶差分进行单位根检验。从表1 中可以看出,原序列的ADF 统计值均大于1%、5%和10%水平下的临界值,P值也都大于0.1,未通过显著性检验,说明原序列价格数据存在单位根。但对原序列价格数据的一阶差分序列做ADF 检验,发现其ADF 统计值均小于临界值,P 值都小于0.01,说明已经通过了显著性检验,即原序列价格数据的一阶差分序列是I (1)过程。基于此,本研究进一步利用B-N 分解法对鸡蛋价格进行趋势周期分解,同时研究其他价格序列变化对鸡蛋价格序列变化的影响程度。

表1 序列ADF 检验
2.2 确定性趋势分析
根据理论指导,本文运用Stata 12.0 对鸡蛋市场价格运用滞后24 项的ARMA 模型对常数项μ 进行估计,选取当AIC 值最小时的μ 值,结果发现,鸡蛋价格μ 值为0.029 0,初始值分别为1.733 3。由此可根据公式Dt=y0+μt计算出确定性趋势以及确定性趋势在原始值中所占的比值。根据图3 可知,自2000 年1 月以来,我国鸡蛋价格一直保持着平稳增长的确定性趋势。2000 年以来,我国进入经济快速发展的时期,人口增多,人民生活水平不断提高,鸡蛋营养价值丰富,食用方便,消费需求不断增加。确定性趋势成分反映的是价格的潜在发展趋势。如果大于100%,说明外部冲击拉低了价格走势,即外部冲击对价格具有抑制作用,反之,则说明外部冲击对价格的增长具有推动作用。由图2 可知,2000—2014 年间,鸡蛋价格的确定性趋势占原序列的比值绝大部分要大于100%,比重均值为106.21%,说明从价格的历史趋势上来看,外部冲击对鸡蛋价格体现出抑制作用。从不同时间段的角度来看,只有2014 年5、7、8、10、11 月5 个月中,该比重低于100%,在这5个月中,外部冲击对鸡蛋价格具有推动作用,其他时期内表现为抑制作用。总体来看,外部冲击对鸡蛋价格变动有抑制作用。

图2 鸡蛋价格的确定性趋势和确定性趋势占原序列比重
2.3 价格波动周期分析
由理论的推导可知,序列ωt=Δyt-μ,φ 最优ARMA模型AR 前的系数,经过Stata12.0 选取,滞后9 阶的AIC值最小,可以作为最优阶数,AR 前的系数为0.203 7,根据,计算出Ct。根据鸡蛋价格波动周期图,本文选取较低的波谷之间为1 个周期,详细划分如表2。可以将我国鸡蛋价格波动周期划分为7 个周期,第3 个周期最长为34 个月,在2003 年8月—2006 年6 月期间发生了剧烈的波动,主要原因是2003 年的非典,2005—2006 年的禽流感疫情对鸡蛋价格变动带来了不同程度的冲击,致使鸡蛋价格在此阶段类波动程度剧烈,波动周期比较长。此外,在2006 年7 月—2009 年1 月之间第4 个周期内鸡蛋价格波动也比较剧烈。第5、6、7 个周期逐渐稳定在18 个月左右,鸡蛋的生产周期大概17 个月,这和鸡蛋的生产周期比较吻合。鸡蛋价格呈现波动主要与突发事件(禽流感疫情影响等等)以及节日效应相关[7]。从研究结果可以看出,鸡蛋价格波动的周期逐渐处于平稳的状态。2014 年1 月之后,鸡蛋价格波动已经进入了第8 个周期中。

表2 我国鸡蛋价格周期划分
2.4 随机趋势分析
由以上分析可知,随机冲击对我国鸡蛋市场价格影响较大,而随机游走描述的随机趋势是各类随机冲击效应的积累。通过BN 分解法可以得到鸡蛋价格的确定性趋势成分和周期成分,根据理论,可以根据St=yt-Dt-Ct来计算出随机成分St,随机趋势大部分时间都处于0 之下,只有少部分大于0,年度均值约为-0.113 2,而各年度随机趋势值占原值比重的均值-6.176 6%,为说明外部冲击对鸡蛋市场价格的冲击作用总体表现为负作用,对鸡蛋价格的负影响比较大。表现出正影响的时间只有2014 年1—7 月。
3 鸡蛋价格冲击影响及随机冲击分析
3.1 鸡蛋价格的冲击作用分析
上文用B-N 分解法分析了鸡蛋价格的波动规律,下一步需要进一步研究影响鸡蛋价格波动的因素。鸡蛋价格波动除了本身供求的因素影响之外,也会受到商品代蛋雏鸡价格、蛋鸡配合饲料价格因素影响,这些因素在生产鸡蛋时不可或缺。为定量研究各因素对鸡蛋价格波动的影响,本文拟建立VAR 模型。首先需要进行单位根检验和协整检验。单位根检验的结果如表1,所有价格序列的一阶差分是平稳的。鸡蛋价格、商品代蛋雏鸡价格、蛋鸡配合饲料价格均为同阶单整I (1)序列,可利用Johansen检验来确定这些变量间是否存在协整关系,协整检验的滞后阶数通过VAR 模型的AIC 值确定。从表3 中可知,迹检验和最大特征值检验表明,至多存在4 个协整关系,说明鸡蛋价格与相关产业之间存在着长期稳定均衡的关系。

表3 鸡蛋市场价格Johansen 协整检验结果
3.2 VAR 模型建立与分析
通过构建VAR 模型,可以分别研究蛋鸡配合饲料价格、商品代蛋雏鸡价格对于鸡蛋价格变化的影响。本研究先用脉冲响应图来直观地反应相关因素对于鸡蛋价格波动的影响。由图3 可以看出,给蛋鸡配合饲料价格一个正的冲击,鸡蛋价格在第1、2 个月内存在一个较小的负响应,然后负响应持续变小,第3 个月里有一个小小的正响应,在第4 个月内的负响应最大,在第5 个月内正响应最大,第6 个月经历一个小小的负响应之后,第7 个月开始进入较小的正相应阶段,第10 个月开始逐渐趋于平稳。说明虽然蛋鸡配合饲料是鸡蛋生产非常重要的要素,但蛋鸡配合饲料价格上涨,并不会马上引起鸡蛋价格上涨,蛋鸡配合饲料价格变化5 个月后才会对鸡蛋价格变化产生影响,即蛋鸡配合饲料价格变化对鸡蛋价格变化的影响有一定的时滞。从图4 可以看出,给商品代蛋雏鸡一个正冲击,在第2 个月内对鸡蛋价格有最大的正影响,然后震荡变小,到第8 个月开始逐渐趋于0,其后几乎为0,这表明商品代蛋雏鸡价格对鸡蛋价格变化反应比较敏感,商品代蛋雏鸡价格对鸡蛋价格变化影响会持续8 个月左右。商品代蛋雏鸡是鸡蛋生产中的重要成本,因此蛋雏鸡价格变化会较快的传导给鸡蛋价格,而且持续时间也相对比较长。

图3 鸡蛋价格对蛋鸡配合饲料价格变化脉冲响应
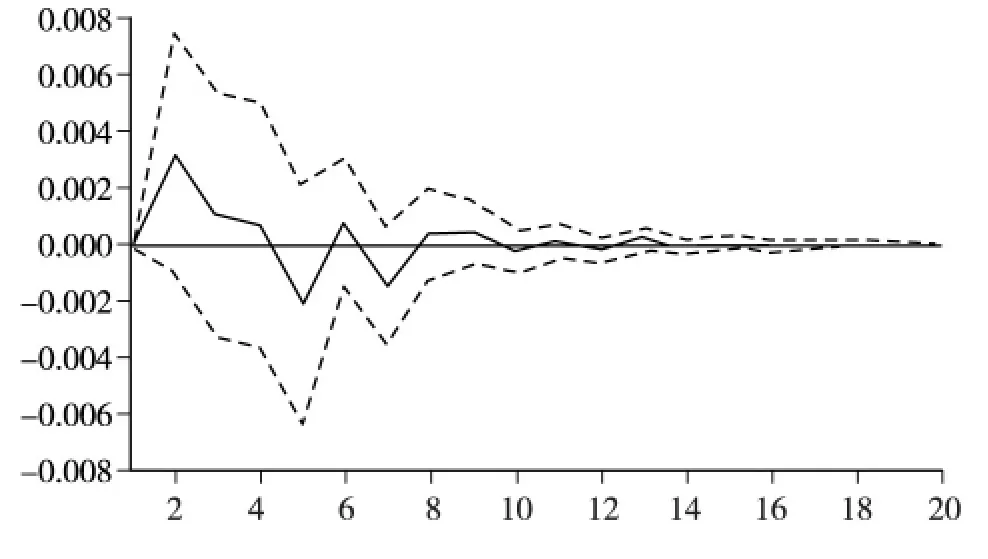
图4 鸡蛋价格对商品代蛋雏鸡价格变化响应
进行脉冲响应分析后,可利用方差分解技术来定量分析蛋鸡配合饲料价格、商品代蛋雏鸡价格对鸡蛋价格的贡献程度。由表4 可以看出,鸡蛋价格在第1 个月只受到自身波动冲击、蛋鸡配合饲料价格波动的影响。从第2个月开始,各个价格序列对鸡蛋价格的影响逐渐显现出来,自身供求的扰动逐渐下降,最后维持在69.37%,可见其自身供求关系的主要作用不可忽视。此外,其他价格序列的冲击影响存不断上升,到最后,各价格序列对鸡蛋价格波动的贡献率分别为:蛋鸡配合饲料为11.70%、蛋雏鸡价格为3.05%。可以看出,在本文所研究的所有价格序列中,蛋鸡配合饲料价格的变化对鸡蛋价格变化影响比商品代蛋雏鸡价格的影响要大一些。

表4 Cholesky 方差分解图
3.3 随机冲击分析
鸡蛋价格不仅受到蛋鸡配合饲料价格、蛋雏鸡价格和替代品价格的影响,同时还受到如禽流感、火箭蛋、雪灾等突发事件的影响,这些突发因素在一定程度上加剧了鸡蛋价格的波动。为测定随机冲击对于鸡蛋价格的长期影响程度,可利用Cochrane (1988)提出方差比统计量,利用LNEP 的一阶方差(记做V1)度量其短期波动。LNEP 的一阶差分的方差可以度量随机成分的波动;LNEPt为向前k 阶差分的方差(即Vk=var (LNEPt+k-LNEPt)),随着k 而趋于无穷大,度量鸡蛋价格的长期波动。基于此,Cochrane 定义的方差比为:Rk=Vk/kV1,令k 趋于无穷大,则有R=limk→∞Rk,R 所度量的是随机冲击对牛肉价格波动的长期影响。Cochrane 证明了R 在量上等于随机趋势的方差与鸡蛋价格总方差之比。R 越大,说明鸡蛋价格的随机趋势对鸡蛋价格波动所起的作用也越大[8]。根据此方法,计算本文部分方差统计比,并计算出方差统计比图。由图5 可以看出,随机冲击对我国鸡蛋价格的影响非常大,一次随机冲击发生后,在第1 个月有一个短暂的缓和,从第2 个月开始,对鸡蛋价格的影响程度逐渐增加,到第5 个月是达到了小的波峰,经过第6 个月小幅下降,第7 个月又开始不断增加,至第9 个月,这次随机冲击的影响达到最大,Rk为1.24,从第11 个月开始,这次随机冲击的影响开始下降,到第30 个月是,随机冲击的影响基本稳定,R 收敛于40%,表明在鸡蛋价格的长期波动中,随机冲击所起的作用高达40%。这一结果说明了随机冲击是加剧我国鸡蛋价格波动和周期形成的主要原因,价格中随机趋势对其波动的影响具有持久而费衰减为0 的特点。此外短期的随机冲击对鸡蛋价格波动的影响一直处在100%以上,即不论从长期还是短期来看,随机冲击对于鸡蛋价格波动及其周期有重要的影响,因此尽可能地减小随机冲击的影响对于稳定鸡蛋价格市场有重要意义。

图5 随机冲击对鸡蛋价格的持久效应
4 研究结论及启示
本文采用B-N 分解法对鸡蛋价格进行趋势周期分解,同时用VAR 模型分析了相关价格对鸡蛋价格波动的影响,并且分析了随机冲击对于鸡蛋价格波动的影响,可以得出如下结论:
(1)我国鸡蛋价格存在平稳的确定性趋势和负的随机趋势,即鸡蛋价格长期稳定增长,随机冲击对鸡蛋价格的波动总是负向的。自2000 年以来,鸡蛋价格波动可以划分为7 个周期,鸡蛋价格的波动周期由剧烈波动逐渐变成规律波动,目前正处于第8 个周期之内。说明鸡蛋市场的自我调节能力较强,本着产业为本的理念,国家应该处理好突发事件的影响,如果能够将突发事件的影响降至最低,鸡蛋价格市场会逐渐处于和生产周期一样的规律波动。(2)根据VAR 模型的方差分解测定可知,鸡蛋价格由于自身供需影响贡献份额为69.36%,不可忽视;蛋鸡配合饲料价格的贡献份额分别为11.70%,贡献份额较大;商品代蛋雏鸡价格的贡献份额为3.05%。因此,为保证鸡蛋价格稳定,需要主要调整鸡蛋市场供需,同时要保证和鸡蛋相关要素市场的价格稳定。因此,调整鸡蛋价格波动的相关政策也要考虑相关产品替代品的价格波动情况。(3)诸如禽流感等随机冲击对鸡蛋价格影响较大,短期随机冲击对鸡蛋价格波动的影响超过100%,从长期来看,随机冲击对鸡蛋价格波动的影响为40%,不可忽视。因此,当突发事件发生时,相关部门应该充分以保护产业为主,把控宣传角度,尽可能让随机冲击对鸡蛋价格波动的影响程度降到最低。
[1]李哲敏,等.中国禽蛋产业链短期市场价格传导机制[J].中国农业科学,2010,43(23):4951-4962.
[2]刘明月,陆迁.突发性疫情事件对新疆鸡蛋价格波动的随机冲击效应研究[J].中国软科学,2013,11:66-72.
[3]谭银清,王钊,陈益芳,等.我国鸡蛋价格波动的特点及影响因素分析[J].畜牧与兽医,2015,47(1):125-129.
[4]黄体冉,等.北京市鸡蛋及其相关行业市场分析及展望[J].中国农学通报,2015,31(2):13-21.
[5]王明利,李威夷.生猪价格的趋势周期分解和随机冲击效应测定[J].农业技术经济,2010,12:68-77.
[6]王明利,石自忠.我国牛肉价格的趋势周期分解与冲击效应测定[J].农业技术经济,2013,11:15-23.
[7]于海鹏,等.2013 年国内外禽蛋市场及贸易形势分析[J].中国食物与营养,2014,20(4):50-52.
[8]Cochrance,J.H.How Big is the Random Walk in GNP?[J].Journal of Political Ecomonics,1988,10:893-920.

