基于近似模型的电连接器接触件分离力计算

汪日超，陈仲海，张 波

(杭州航天电子技术有限公司，浙江杭州，310051)

1 引言

电连接器作为一种基础元器件，用于实现电信号的传递和控制以及电子与电气设备之间的连接，在电子、机械、航空、航天等行业中应用广泛，发挥着重要的作用［1］。实现电连接器连接功能的是集成在电连接器绝缘体内部的多对接触件，任何一对接触件的失效都会对整个系统的可靠性造成影响。因而，研究和开发高可靠性的电连接器接触件对提高系统的可靠性具有至关重要的作用。

目前，针对接触件插拔过程的力学研究较少，接触件在插拔过程中产生的插拔力没有统一的计算公式，且公式精度较低。随着计算机的应用和发展以及有限元方法的成熟，近年来发展了电连接器静态结构的数值模拟技术，接触件插拔过程的研究领域逐步引入了有限元数值模拟技术。

本文旨在建立接触件分离力与接触件结构几何参数的关系函数，从而可以快速计算接触件分离力。通过实验验证了该方法的有效性，为设计高可靠性的电连接器提供了理论依据和方法，对航天元器件具有重要的意义。

2 接触件插拔力理论分析

电连接器主要采用圆柱式接触件、麻花式接触件、双曲线式接触件等三种结构。其中，圆柱式开槽接触件是最常用的接触件结构，如图1所示。插针与插孔插合时，依靠插孔簧片结构发生弹性变形产生接触压力。为了具体分析簧片结构参数与接触压力的关系，可将圆柱式开槽接触件简化成图2所示的悬臂梁结构，其产生的接触压力F为:

式中，L为悬臂梁长度;δ为挠度;E为弹性模量;I为横截面的惯性矩。

图1 圆柱式开槽接触件

图2 悬臂梁简化模型

插合时，接触件接触面之间的力由两部分组成，如图3所示。其中，Ft为摩擦力，Fn为法向接触压力，接触面之间的摩擦因数记为μ，则有Ft=μFn。插针的插入力记为Fi，则接触件在三个力的作用下达到力学平衡，如图3a所示。根据力学分析进一步可得，插孔的接触压力F和插入力Fi的关系式如下:

式中，α为摩擦力与接触件轴线的夹角。

图3 接触件接触示意图

用r1和r2分别表示插针头部球体半径和插孔内孔倒角半径，并结合图4进行分析［2］。

α初始值α0为:

结合图4可以得到，当插入量为s时，插孔产生的挠度为:

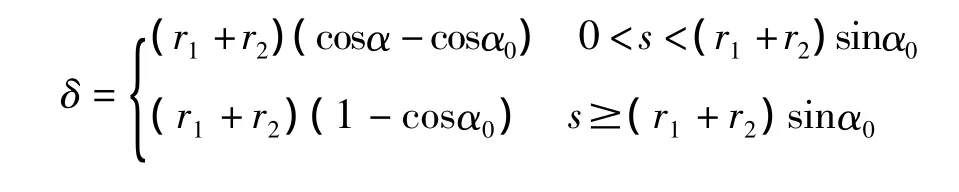
图4 插入过程示意图

结合公式(1)和公式(2)，可以运用Matlab进行计算和绘图，得到接触压力、插入力随插入量的变化曲线分别如图5和图6所示。

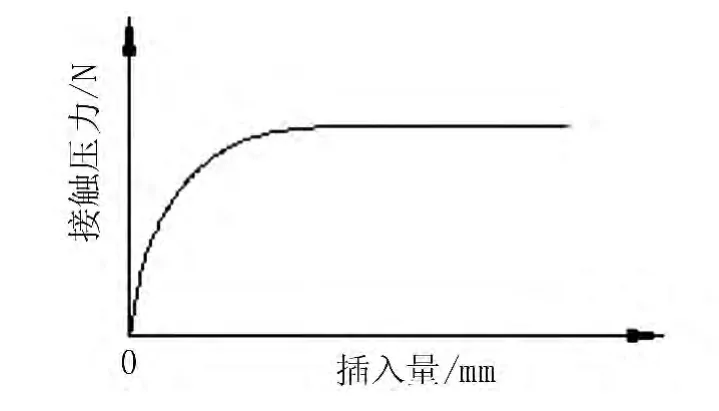
图5 接触压力变化曲线图

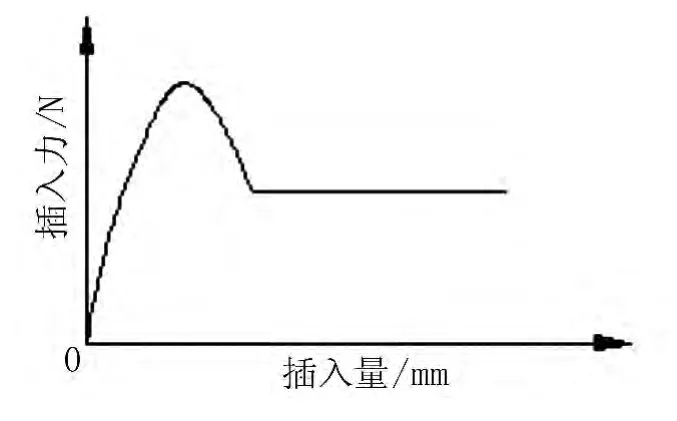
图6 插入力变化曲线图

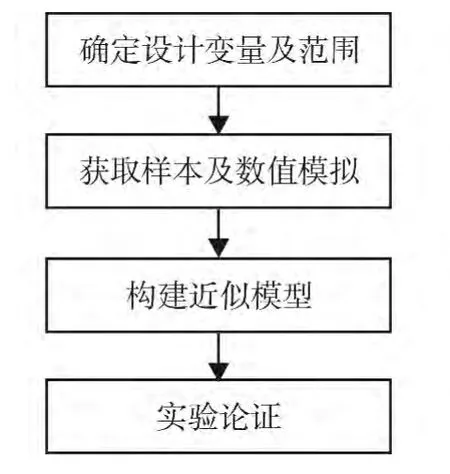
图7 接触件分离力计算流程

从图5和图6中可以看出，由于针头头部的影响，接触压力是随插入量不断变大的过程，当头部完全插入时，接触力趋于稳定。在此过程中，插入力出现一个峰值，然后减小并趋于稳定。但是，插入力的最大值和接触压力的最大值不是同时出现，这是由于存在倒角的缘故。国标中对插入力的最大值和稳定值均有相应的规定，以保证接触件的可靠性。在进行接触件设计时，希望增大接触件间的接触压力，即增大稳定后的插入力，同时减小插入力峰值。由于接触件分离时，只受到摩擦力的作用，分离力的大小和插入力稳定后的大小相同，所以也可以将插入力稳定值称为分离力。

3 计算流程

计算流程主要包括提取接触件结构参数，确定设计变量及其变化范围;应用试验设计方法获取设计变量的n个设计参数样本点的分布，n组样本点数值模拟;建立分离力与样本点之间的对应关系表，并依此建立分离力与设计变量之间的近似模型函数;实验论证。计算流程如图7所示。

4 近似模型的建立

4.1 设计变量的确定

设计变量一般选取对质量目标影响显著的因素，影响接触件分离力大小的因素很多，包括接触件的力学性能参数、工艺参数和接触件结构参数几个部分。其中，力学性能参数为弹性模量、切线模量;工艺参数为摩擦系数;结构参数包括:开槽长度L、开槽宽度B、插孔外径 D、插孔内径 d、插孔内孔倒角半径R、槽宽同轴度e、收口尺寸φ。对于特定材料和工艺条件的接触件，其弹性模量和摩擦系数为常数。根据文献［3］，槽宽同轴度e对接触件的影响很小，不作为本文的设计变量，收口尺寸φ=0.75D，插孔外径D=1.5d。设计变量信息如表1所示。

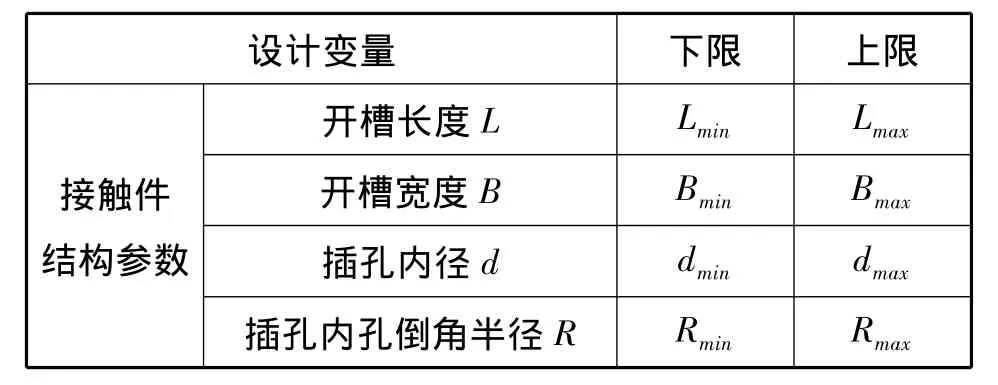
表1 设计变量信息表

4.2 实验设计的选择

在响应面近似模型的构造过程中，试验点的选择是十分重要的。试验设计点的合理取样可以帮助构造更为精确的近似模型。本文采用均匀拉丁方试验设计［3］构建响应面近似模型的样本。对于非线性问题，通过均匀拉丁方试验设计不但能减少试验次数，而且构造的响应面模型精度较高。

4.3 响应面近似模型

常用的代理模型［4］有:响应面模型、径向基函数模型、人工神经网络模型和Kriging模型等。径向基函数与Kriging模型所需要的计算量大，人工神经网络需要大量的样本点，而多项式响应面模型由于形式简单，计算量小等优点，因此在因素较少的情况下广为应用。

响应面法(Response Surface Methods，RSM)［5－7］是以试验设计为基础的，用于处理多变量问题和分析的一种数量统计技术。其基本思想是在试验测量、经验公式或数值模拟的基础上，对整个设计空间子域内的设计点集合进行连续的试验求值，从而得出真实响应值的全局逼近。响应面模型关系式的一般形式为:

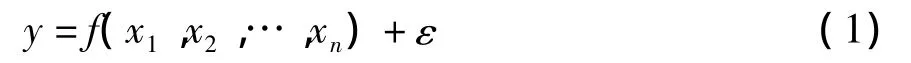
式中，ε为随机误差，一般假设其满足均值为0的正态分布;x1，x2，…，xn为设计变量;n为设计变量的个数;f为设计变量的响应。

RSM中常用一次、二次、三次或四次多项式进行回归分析。本文采用相对简单却有较高准确性的二次多项式拟合模型，如式(2)所示:

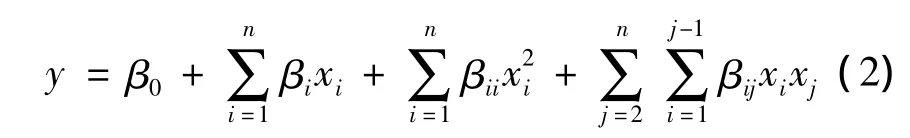
建立的二阶响应面模型精度需要通过决定系数检验，决定系数R2和调整后的决定系数Ra2，如果R2和Ra2越接近1，表示模型越为精确。

5 算例研究

本文以某分离脱落电连接器接触件为研究对象，运用Ansys有限元仿真软件对接触件进行仿真。该接触件的有限元仿真模型如图7所示，接触件材料为锡青铜QSn4－3，弹性模量为1.1×1011Pa，切线模量为3×109Pa，泊松比为0.33，摩擦系数为0.16，仿真得到的分离力曲线如图8所示。

根据接触件的性能参数和使用要求，各设计变量的取值范围如表2所示。

图7 接触件有限元模型

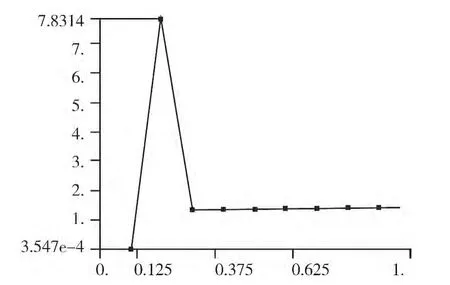
图8 插拔力变化曲线图

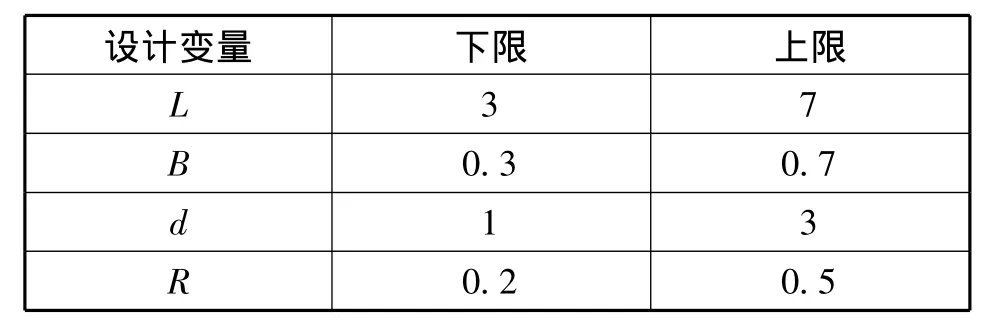
表2 设计变量变化范围表(单位:mm)

本文通过均匀拉丁方试验设计抽取20组样本点，完成设计变量在设计空间的采样。数据如表3所示。以J为目标函数，计算出第一个样本点参数对应的分离力F。依此重复该步骤，计算出所有20个样本点对应的分离力F，结果如表3所示。

表3 拉丁方实验数据

根据表3的结果，由此可以构建目标响应J的二次响应面近似模型如下:

式中，x1、x2、x3、x4、y 分别表示 L、B、d、R、F。

其决定系数R2和调整后的决定系数分别为:R2=0.9777;Ra2=0.9153。两者都接近于 1，由此可知，构造出的二阶响应面近似模型精度较高。

6 试验论证

以某分离脱落电连接器接触件为试验论证对象，该接触件结构尺寸为:L=6.5、B=0.6、d=1.6、R=0.3。将参数代入公式(3)，得到分离力F=1.505N。

将接触件装入插拔力测试设备中，如图9所示。测得分离力F=1.52N，与近似模型公式得到的结果基本一致。

图9 接触件分离力检测图

7 结语

(1)本文以电连接器接触件为研究对象，进行了插拔力理论分析，建立了插拔力与结构参数之间的关系;

(2)建立了接触件有限元仿真模型，运用Ansys软件对接触件插拔过程进行了仿真，得到接触件的分离力;

(3)运用响应面法，建立接触件分离力与接触件结构参数的关系函数，并通过实验论证了该方法的有效性。

［1］ 任国泰.电连接器基本知识(1)［J］.机电元件，2004，(1):42 －45.

［2］ 潘俊，靳方建，陈文华，钱萍.电连接器接触件结构分析与插拔试验［J］.中国机械工程，2013，(12):1636－1641.

［3］ Hickernell F J.A Generalized Discrepancy and Quadrature Error Bound［J］.Mathematics of Computation，1998，67(221):299 －322.

［4］ 张渝，周杰，安治国.基于响应面方法的汽车法兰盘锻模优化设计［J］.热加工工艺，2009，(21):104－107.

［5］ 张峻，柯映林.基于动态序列响应面方法的钣金成形过程参数优化［J］.中国机械工程，2005，16(4):307－310.

［6］ 陈文琳，邹文超，曹俊.基于响应面法的板料成形工作模面参数优化［J］.农业机械学报，2009，40(11):236－239.

［7］ 熊俊涛，乔志德，韩忠华.基于响应面法的跨声速机翼气动优化设计［J］.航空学报，2006，27(3):399－402.