电磁场边界条件的研究*＊

刘 豪

(河南城建学院电气与信息工程学院，河南平顶山467036)

0 引言

对于不同媒质所组成的区域，由于在分界面上媒质参数会发生突变，而且矢量场也可能会发生突变，因此必须采用多种媒质所组成的区域分析。

无论是在含有单一媒质的区域中还是在含有多种煤质的区域中，宏观时变电磁场都满足如下积分形式的麦克斯伟方程组［1～4］

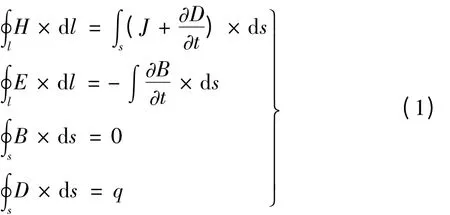
式中，l—区域中的任意闭曲线;S—区域中的任意闭曲面;B—磁通密度;D—电位移;t—时间;q—闭曲面S 所包围的电荷。

当场量在积分区域中存在连续偏导数时，各常量满足如下微分形式的麦克斯伟方程组［1～4］

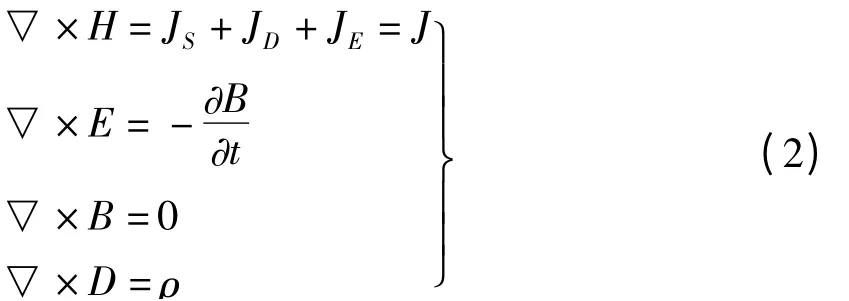
式中，JS—区域内外源的电流密度;JE—导电媒质中的涡流密度;JD—位移电流密度;ρ—区域内自由电荷的等效体密度。

1 从电学角度推导边界条件

设两种媒质的介电常数分别为ε1、ε2，磁导率分别为μ1、μ2，如图1、图2 所示。

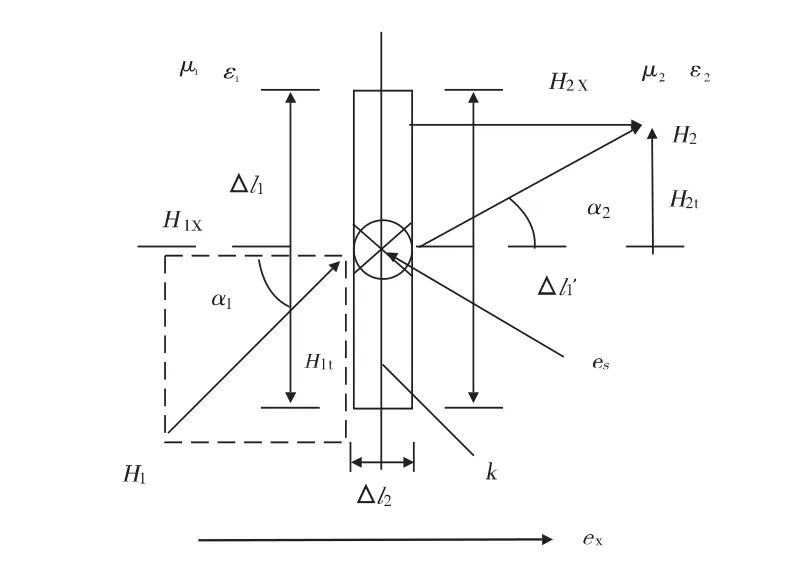
图1 跨两种媒质的分界面

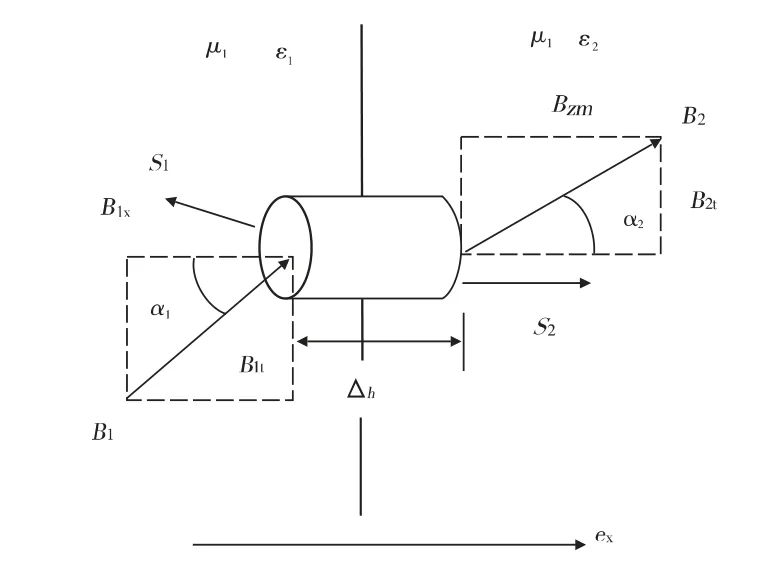
图2 跨两种媒质的分界面

1.1 全电流定律

1.2 磁路节点定理

2 从数学角度推导

2.1 多曲面斯托克斯公式

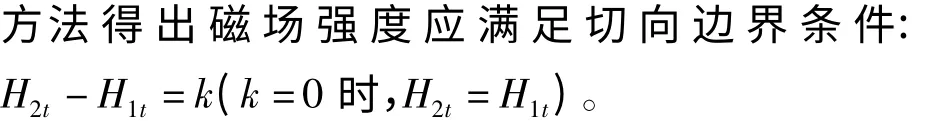
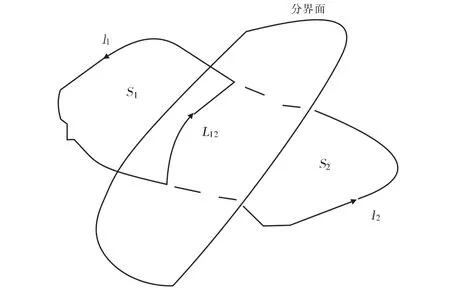
图3 跨分界面的任意曲面

2.2 多区域高斯公式

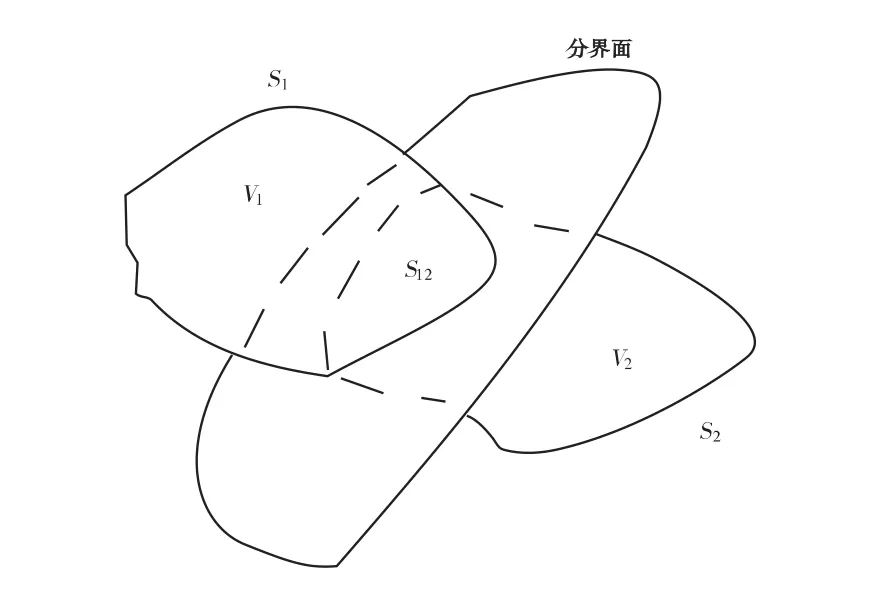
图4 跨分界面的任意曲面

利用多区域高斯公式可得

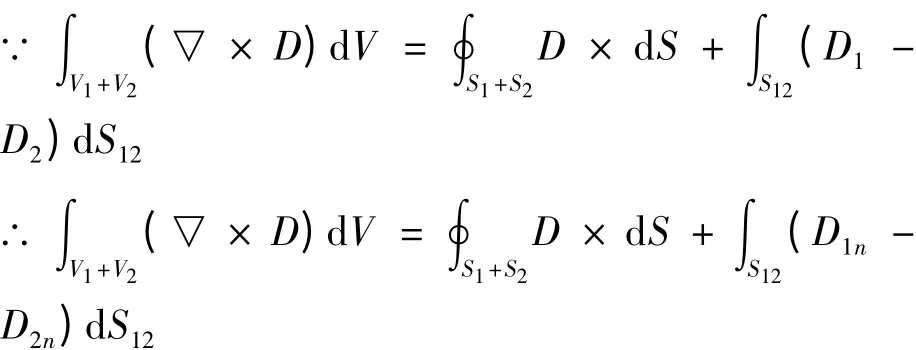
3 结语

本文从不同角度研究电磁场边界条件。从研究的过程来看:第一种方法要根据很多定理以及右手定则，推导起来要综合多方面的知识;第二种方法应用高斯公式、斯托克斯公式以及麦克斯伟方程组即可推出。因此第二种方法比第一种方法简单。从应用来看，对于多种媒质采用第二种方法比第一种方法较易于掌握，但二者都满足电磁场的边界条件。不管是第一种方法还是第二种方法，从研究的公式来看，旋度源可能引起场的切向分量突变，散度场可能引起场的法向分量突变。如果没有偶极矩，无散场的法向分量一定连续，无旋场的切向分量一定连续，对于调和场这种突变都不存在。

［1］ 冯慈璋，马西奎. 工程电磁场导论［M］. 北京:高等教育出版社，2000.

［2］ 古恩(Guru，B.D.)［美］.电磁场与电磁波(英文)［M］.北京:机械工业出版社，2002.

［3］ 雷银照，徐纪安.时变电磁场唯一定理的完整表述［M］.北京:电工技术学报，2000，15(1):16-20.

［4］ 盛祥耀.数学手册(大学生用)［M］. 北京:清华大学出版社，2008.11.

［5］ 黎滨洪，金荣洪，张佩玉.电磁场与波［M］.上海:上海交通大学出版社，2001.02.