屏蔽电动机Π 型精确等效电路及参数计算

陈春光

(上海精基实业有限公司，上海200333)

0 引言

屏蔽式三相异步电动机(以下简称“屏蔽电动机”)是在一般三相异步电动机的基础上，在转子铁心外圆和定子铁心内圆各安装一个圆筒形、两端封闭的金属套筒(即为屏蔽套)构成。屏蔽电动机运行时，以同步转速旋转的合成磁场在屏蔽套内产生感应电势和涡流，产生涡流损耗，进而影响电动机性能指标。目前，国内多数还是采用Γ型等效电路来分析和计算电动机性能，未能在等效电路中考虑屏蔽套损耗的影响参数，导致计算误差偏大。

本文在三相异步电动机T 型等效电路的基础上，结合复合转子电机理论，充分考虑屏蔽套的影响因素，构建了屏蔽电动机Π 型精确等效电路，并提出了屏蔽套阻抗参数的计算方法，使得屏蔽套损耗可以在等效电路中计算出来。

以一台功率为37kW，极数为2 的屏蔽电动机为例，应用屏蔽电动机Π 型精确等效电路，进行性能分析和计算，与采用传统Γ 型等效电路计算结果，同试验值对比，分析两种计算方法的精度，寻求定、转子屏蔽套参数的计算方法，更好地为工程应用拓展途径。

1 屏蔽电动机传统Γ 型等效电路

电机内部理论属于“电磁场”问题，电磁场的理论分析和计算比较复杂，习惯上简便地把“场”的问题转换成“路”(即电路和磁路)的问题。电机经典分析方法是把电路和磁路又简化为单一电路问题，即归算后等效电路分析［1］。等效电路是分析和计算电机性能的主要工具。这样，等效电路的精确性直接影响到电机性能分析结果的准确性。

在三相异步电动机T 型等效电路(如图1 所示)的基础上，励磁支路中略去定子电阻R1、定子漏抗X1和励磁电阻Rm，得到简化等效电路，即Γ 型等效电路，如图2 所示。目前，国内多数电磁计算仍采用电机行业通用的《中小型三相异步电动机电磁计算程序》(1971 年版)，该计算程序以美国西屋公司40 年代的计算程序为基础［2］，仍是建立在简化等效电路基础上的，存在较多简化和假设条件。

Γ 型等效电路励磁支路全为无功电流，定子有功电流等于转子有功电流，从而在电磁计算过程中避开了由于转差率s 未知而造成的计算困难，以效率作为迭代量判断校核是否完成［3］。

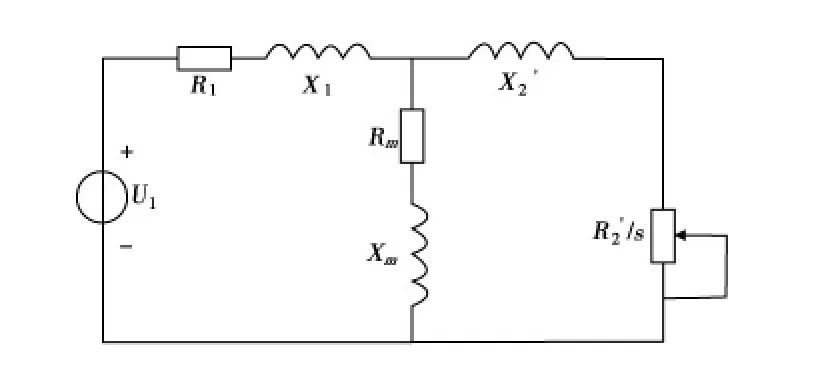
R1—定子电阻;X1—定子漏抗;Rm—激磁电阻;Xm—激磁电抗;R2'—归算后的转子电阻;X2'—归算后的转子电抗;s—转差率。图1 三相异步电动机T 型等效电路

图2 三相异步电动机Γ 型等效电路

屏蔽电动机传统Γ 型等效电路采用图2 三相异步电动机Γ 型等效电路，屏蔽套损耗影响参数不在该等效电路中体现，而是使用经验公式［4］

计算屏蔽套损耗，并在计算过程中把这项损耗当作固定值。这样做的不足之处一是没有考虑屏蔽套的存在对电机等效电路的影响，造成电路模型无法反映实际电机中的屏蔽套结构;二是转差率变化时，定、转子屏蔽套的涡流损耗也随之变化，不能简单地都以额定工况时的数值代替，否则无法准确反应起动过程。这两方面因素必然造成按照传统方法计算的屏蔽电机性能指标的计算结果有较大误差。为提高计算精度，减小计算误差，需对等效电路进行改进，将屏蔽套参数引入到等效电路中，并且不做简化处理，尽可能接近真实物理模型。

2 屏蔽电动机Π 型精确等效电路

由于屏蔽套材料的磁导率很低，接近空气的磁导率，而且屏蔽电动机的气隙又大于感应电机，其等效电磁间隙可达相近规格感应电机4 ～5 倍，激磁电流显著大于一般三相异步电动机。因此，与一般三相异步电动机相比，屏蔽电动机的功率因数低、电流大［5］。

气隙旋转磁场感生的屏蔽套涡流损耗又使电机的效率降低。基于以上分析，在感应电机Π 型精确等效电路的基础上［2，6］，激磁支路和转子支路分别并联定、转子屏蔽套支路，定、转子屏蔽套结构等效为电阻和电感串联的形式，则得到屏蔽电动机Π 型精确等效电路，如图3 所示。

R1—定子电阻;X1—定子漏抗;Rm—激磁电阻;Xm—激磁电抗;R2'—归算后的转子电阻;X2'—归算后的转子电抗;Rc1—定子屏蔽套电阻;Xc1—定子屏蔽套电抗;Rc2'—归算后的转子屏蔽套电阻;Xc2'—归算后的转子屏蔽套电抗。图3 屏蔽电动机Π 型精确等效电路

如果移除图1 虚线框内的结构，就变为感应电机的Π 型等效电路。屏蔽套电阻的计算式为［7］

式中，m1—定子相数;Nφ1Kdp1—定子绕组每相有效串联导体数;L—屏蔽套内涡流路径的轴向长度;ρc—屏蔽套材料的电阻率;D—通过屏蔽套径向中心线的直径;δ—屏蔽套厚度;s—转差率;Ke—端部系数［8，9］。

2.1 屏蔽套轴向涡流长度L 的确定

实际的屏蔽电动机中，为了将绕组端部等结构保护在内，屏蔽套的长度要大于定、转子铁心长度。屏蔽套内的涡流路径不只局限在铁心长度范围内，而是经由屏蔽套两端位于铁心长度以外的端部闭合。端部效应用端部系数Ke(＞1)来表示，其影响体现为屏蔽套内涡流损耗的减小、即电阻的增加。在计及端部效应的基础上，尚需确定屏蔽套内轴向涡流长度L。

文献［10］通过建立双屏蔽复合转子电机的三维端部模型，研究了定、转子屏蔽套端部涡流电密和涡流损耗密度的空间分布情况。分析可知，L 与屏蔽套内涡流路径的实际分布有关，应为铁心长度、屏蔽套长度的函数。L 综合考虑，屏蔽套内涡流区域的轴向长度L 可表示为

式中，lt—铁心长度;lc—屏蔽套长度;Kcan—屏蔽套轴向涡流长度的修正系数。

通过与不同额定功率、两极屏蔽电机的试验数据对比，使用该方法时，屏蔽套涡流损耗的计算结果与试验结果吻合较好(见表1)。

表1 屏蔽套涡流损耗的计算值与试验值对比

2.2 起动过程中屏蔽套涡流损耗的变化情况

起动过程中，电势系数Ke逐渐增大，由屏蔽电动机Π 型精确等效电路(图3)可知，定子屏蔽套的涡流损耗逐渐增大;而转子屏蔽套两端的电压与定子屏蔽套两端电压相同，其大小均为感应电动势KeU1，因此同一转差率s 时，定转、子屏蔽套的涡流损耗在数值上应存在某种关联。

根据式(2)，转子屏蔽套电阻的计算式为

其物理意义，把转子屏蔽套看作是一相、每相串联导体数为1 的绕组，将其向定子侧进行相数、有效匝数和频率的归算，得到转子屏蔽套电阻的归算值Rc2'，且

根据电机学理论，Rc2'上消耗的功率可分为两部分，s 部分转化为转子屏蔽套内的涡流损耗，(1-s)部分则产生驱动性质的电磁转矩。因此，在某一感应电动势KeU1时，转子屏蔽套的涡流损耗为

在计算定子屏蔽套的电阻时，只需进行相数和有效匝数的归算，而不用进行频率归算。令式(2)中转差率s=1，则定子屏蔽套电阻的归算值为

通常情况下，定、转子屏蔽套采用同种材料，如果二者厚度相同，且忽略定、转子屏蔽套直径和定、转子屏蔽套内涡流路径等效长度的差异，有近似关系

即任一转差率时，都有转子屏蔽套损耗约等于定子屏蔽套损耗乘以转差率的平方。以额定功率25kW、2 极的电机为例，其定转子屏蔽套材料均为1Cr18Ni9Ti(电阻率0.72×10-6Ω·μm)，厚度均为0.5mm。计算电机起动过程中的定、转子屏蔽套涡流损耗pc1和pc2，列出部分数据见表2。据此绘出起动过程中定、转子屏蔽套损耗的变化曲线，如图4。

表2 起动过程中屏蔽套损耗数值

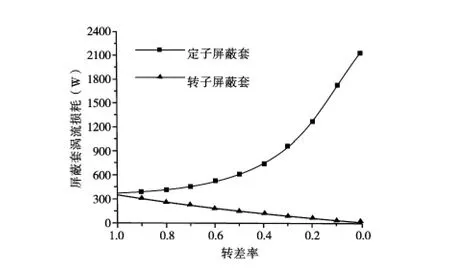
图4 起动过程中屏蔽套损耗变化曲线

对图表数据的分析可得如下结论

(1)任一转差率时，定子屏蔽套涡流损耗pc1、转子屏蔽套涡流损耗pc2以及转差率s 三者之间有式(9)所示的近似关系式成立;

(2)s=1 时，对于相同材料、相同厚度的定、转子屏蔽套，其涡流损耗数值相近，pc1仅略大于pc2。换言之，起动时转子屏蔽套内的涡流损耗已不能忽略;

(3)在起动过程中，定子屏蔽套的涡流损耗逐渐增大，转子屏蔽套的涡流损耗则逐渐减小。

3 实例计算

一台屏蔽电动机功率为37kW，极数为2，主要计算参数见表3。

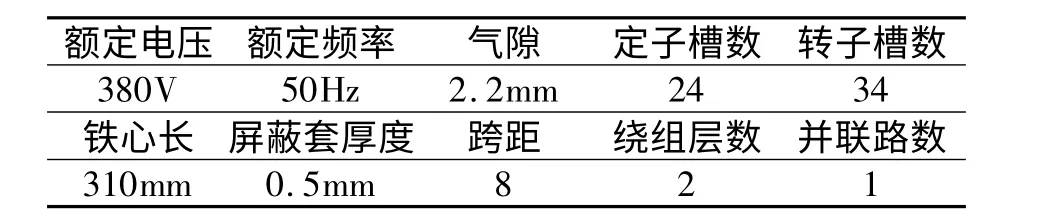
表3 屏蔽电动机主要计算参数

应用屏蔽电动机Π 型精确等效电路，对该电动机进行性能分析和计算，与采用传统Γ 型等效电路计算结果，同试验值对比，如表4 所示。

表4 本文方法与传统方法计算精度对比

表4 中，η 为额定效率;nN为额定转速;cosφ为额定功率因数;Ist为堵转电流倍数;Tst为堵转转矩倍数。

从表4 中数据可以看出，额定效率、额定转速的计算结果已非常接近试验值，额定功率因数和堵转电流倍数的百分误差也大幅减小。堵转转矩倍数的误差则略大，但比传统方法而言仍有改善。考虑到堵转试验的测试误差，这样的结果也可接受。

4 结语

本文在感应电机的Π 型精确等效电路基础上提出了屏蔽电动机Π 型精确等效电路，与传统方法(采用Γ 型等效电路计算)相比，计算精度有了明显改善。通过对计算结果与试验数据的对比分析，说明采用本文方法能够根据等效电路计算屏蔽套涡流损耗的数值，并且计算精度较经验公式更高。与传统方法相比，本文方法的计算精度有了明显改善，具有很高的工程应用价值，应用该等效电路开发的屏蔽电动机计算程序可直接应用工程实践。

［1］ 阎治安，崔新艺，苏少平.电机学［M］.西安:西安交通大学出版社，2006:2-3.

［2］ 陈伟华，黄国治. 基于精确等值电路的异步电机第二版电磁计算程序［J］.中小型电机，1992，19(1):2-6.

［3］ 王亚峰，韩力，谭春宇. 基于Π 型精确等效电路的三相异步电机电磁计算程序改进及其探讨［J］. 电机技术，2003(2):3-4.

［4］ 于令新.屏蔽电动机的计算特点［J］.大电机技术，1979(4):24-30.

［5］ Dai Uneyama，Yuji Akiyama，Shinya Manome，and Tomokazu Naruta，The Proposal of Can Loss Estimation Method of Canned Motor［J］.Proceedings of International Conference on Electrical Machines and Systems，2007:882-885.

［6］ 王亚峰.计算机辅助三相感应电动机电磁设计的改进研究［D］.重庆:重庆大学硕士学位论文，2003:1-18.

［7］ 傅丰礼，唐孝镐. 异步电机设计手册［M］.北京:机械工业出版社，2007:640-648.

［8］ R.C.Robinson，I.Rowe，and L.E.Donelan，“The calculation of can losses in canned motors”，Power Apparatus and Systems，Part III.Transactions of the American Institute of Electrical Engineers，vol.76，no.3，pp.312-315，April 1957.

［9］ R.L.Russell and K.H.Norsworthy，“Eddy currents and wall losses in screened-rotor induction motors”，Proceedings of the IEE-Part A:Power Engineering，vol. 105，no.20，pp.163-175，April 1958.

［10］ 张建涛.双屏蔽复合转子电动机涡流损耗计算和性能分析［D］. 哈尔滨:哈尔滨理工大学硕士学位论文，2009:7-33.