改进Verhulst 模型在饱和负荷预测中的应用

尚芳屹，杨宗麟，程浩忠，辛洁晴，顾 洁

（1.上海交通大学电力传输与功率变换控制教育部重点实验室，上海200240；2.华东电网有限公司，上海200000）

饱和负荷是电网规划中确定电网发展最终规模的关键性指标，是近年来电网规划中提出的新概念。通过对一个地区或省市的饱和负荷水平进行分析和预测，有助于确定电网的最终规模，并以远景电网规划为目标指导近期电网规划与建设，可以避免不必要的改扩建工程，有利于促进区域电网建设与经济社会发展相适应。

与传统的针对具体年限的负荷预测特点不同，饱和负荷预测的时间跨度往往较大，且影响因素众多。目前，国内尚缺乏对省级、区域级饱和负荷预测方法的研究，多数是针对城市饱和负荷的研究，不仅对饱和负荷的概念没有明确、定量的定义，而且现有的预测方法也比较有限[1-9]，基本上是采用S 型曲线、人均饱和用电量法、饱和负荷密度法、空间负荷预测法、基于系统动力学预测法等。

饱和负荷预测的对象具有预测时间跨度长、负荷规模增长呈现“S”型的特点。根据负荷的增长规律，借鉴发达国家用电需求的特征，本文提出了对饱和负荷的判定指标集和一种饱和负荷预测方法，将等维新息递补技术引入灰色Verhulst 模型中，并对预测结果进行残差修正，构建一种改进的灰色Verhulst 预测模型。以某电网公司所辖区域内的负荷为例进行饱和预测，说明所提饱和判定指标集的可行性及改进Verhulst 模型的有效性。

1 饱和负荷

1.1 饱和负荷的概念

饱和负荷，亦称为用电需求饱和规模，它涵盖了两个指标，一是该地区全社会用电量进入饱和增长阶段的规模，二是该地区年最大负荷进入饱和增长阶段的规模。倘若某地区负荷随着时间的推移不再有阶跃性增长，而是按照自然规律呈现较平稳的增长状态，则认为该地区的负荷进入了饱和增长阶段，简称饱和阶段。

一个地区的负荷增长通常呈现如下规律：在经济发展初期，用电需求增长较慢；随着经济的快速发展，用电需求出现快速增长的趋势；受土地面积、环境资源、规划定位等因素的制约，该地区的用电需求不会无限制地增长，而是呈现出饱和增长态势，即总体呈现“S”型。根据负荷增长规律，负荷增长分为缓慢增长阶段、快速增长阶段、饱和增长阶段，如图1 所示。

饱和负荷预测对象是一个地区或省市的用电需求，用电需求涉及2 个特征量：一是该地区的全社会用电量，二是该地区的最大负荷，二者从不同角度，反映了该地区的用电需求情况。

1.2 饱和阶段判定指标集

图1 负荷增长阶段图Fig.1 Growth stage graph of power demand

一个地区的电力平衡有利于促进该地区社会经济的发展，而社会经济的发展又可拉动用电需求的增长，因此，仅仅采用用电需求指标对饱和阶段进行界定是很单薄的、不合理的。发达国家和地区的用电需求发展及对应的社会经济背景对我国负荷饱和阶段的界定有重要的指导意义，其负荷饱和阶段的各类指标如表1 所示。

以发达国家和地区的用电需求增长率、饱和年份对应的各项指标为参考，综合考虑负荷进入饱和阶段后的经济社会发展状况，选取了负荷年增长率、产业结构、用电结构、人均用电量、人均GDP、人口增长率作为判断一个地区或省市负荷进入饱和阶段的判定指标，得到负荷进入饱和阶段的判定指标集，如表2 所示，并以此为判据进行饱和负荷的预测。

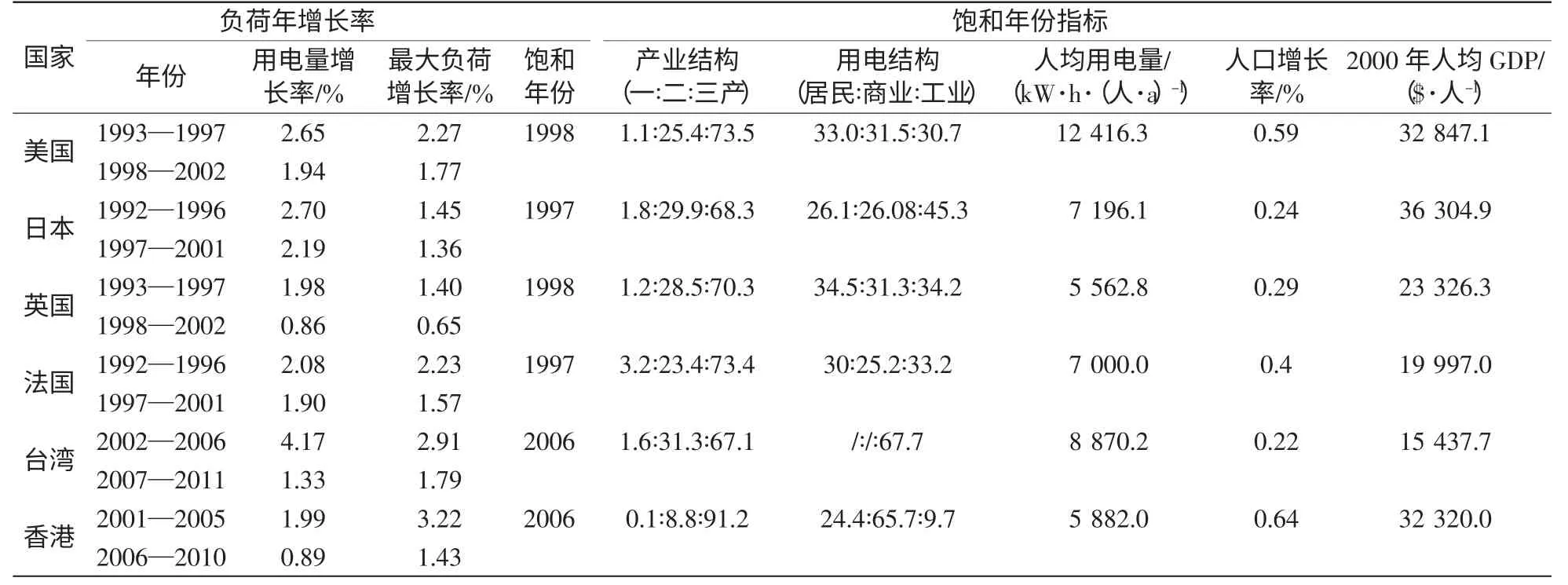
表1 发达国家和地区负荷进入饱和阶段的指标Tab.1 Indices on saturation stage in developed countries and regions

表2 负荷进入饱和阶段的判定指标集Tab.2 Indices on saturation stage

2 改进灰色Verhulst 模型

2.1 灰色Verhulst 模型

灰色Verhulst 模型主要反映了任何事物自身的发生、发展及消亡的过程[10]，可以用来进行具有饱和状态的S 型序列的预测，其建模步骤如下。

步骤1 采集输入数据序列

步骤2 对输入数据序列进行一阶累加（1-IAGO）生成新数列

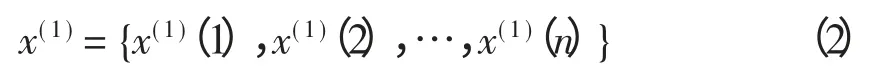
步骤3 对新数列生成紧邻均值生成序列

其中，z(1)（k′）=0.5x(1)（k′）+0.5x(1)（k′+1），k′=1，…，n-1

步骤4 建立灰色Verhulst 模型的白化微分方程

式中：a 为发展系数；b 为灰作用量；t 为时间。

步骤5 最小二乘估计

步骤6 建立灰色Verhulst 模型时间响应方程

步骤7 对式（6）做1-IAGO 累减还原，得到输入数据序列x(0)的灰色Verhulst 预测模型，即

2.2 等维新息递补

在灰色Verhulst 预测的结果中，真正具有实际意义并且预测精度较高的预测值仅仅是整个预测序列中的第1、2 个预测值。根据负荷增长的“近大远小”原则，将等维新息递补处理技术引入到Verhulst 模型中，即每当预测出一个新值时，把它加入到样本序列同时去掉样本序列中最早的1个数据，以保证在序列维数不变的前提下，样本数据中始终含有最新的数据信息，然后据此样本序列重新建立灰色Verhulst 模型，循环下去直到得到目标预测年份的数据为止[10]。采用这种处理方法使预测模型得到有效的修正，其预测精度提高。

2.3 残差修正

将等维新息递补的概念引入Verhulst 模型，以样本数据增长率为输入数据序列得到样本增长率预测序列，还原得到的样本预测序列与样本观测序列对比，求取残差序列[11]，即

其中，e(0)（k）=x(0)（k）-

以残差序列e(0)作为灰色Verhulst 模型的输入，建立灰色Verhulst 残差修正模型，计算残差序列的预测值e(0)来补偿预测误差。

改进灰色Verhulst 模型的预测数据序列为

根据上述分析过程，采用改进的Verhulst 预测方法对用电需求进行饱和预测的总体流程如图2 所示。

图2 改进Verhulst 模型流程Fig.2 Flow chart of improved Verhulst model

3 饱和负荷预测基本步骤

饱和负荷预测的基本步骤如下：

（1）饱和年份预测 采用本文所提的改进Verhulst 模型对电网所辖区域的电力电量序列进行建模分析，并找出其他各指标达标的年份，取其中的最大年份作为饱和年份。

（2）饱和负荷规模预测 饱和负荷的规模采用改进Verhulst 模型的预测结果，根据饱和年份找出对应年份的全社会用电量和最大负荷数值，即可得到该地区的饱和负荷水平。饱和负荷的基本分析思路如图3 所示。

4 实例分析

以某地区电网公司所辖区域1990-2011 年的实际负荷数据、GDP 数据、人口数据[12]为例，对该电网所辖区域内的饱和负荷进行预测，并对预测结果进行评价分析。

据灰色Verhulst 基本模型（模型1）、改进的灰色Verhulst 模型（模型2）对1990-2011 年的用电需求情况进行预测，预测结果以及精度分析见表3。

通过对比分析发现，对于带有饱和趋势的负荷数据，改进的灰色Verhulst 模型预测精度更高，且对全社会用电量、最大负荷的预测具有通用性，因此改进灰色Verhulst 模型更适用于饱和负荷的预测。

图3 饱和负荷分析流程Fig.3 Flow chart of saturation load analysis

按照饱和负荷的分析思路，首先根据判定指标对饱和时间点进行分析，采用改进的Verhulst 模型分析用电需求情况，得到全社会用电量和最大负荷的达标年份。根据该地区的相关研究资料外推得到其他判定指标的达标指标，进而得到该地区的饱和年份，具体数据如表4 所示，改进Verhulst模型预测的未来年份数据。如表5 所示。

通过饱和判定指标的分析与验证，可以得到该电网所辖区域的用电需求于2035 年进入饱和阶段，饱和规模如表6 所示。

表3 某电网所辖区域内的用电需求历史数据、各模型预测数据及误差分析Tab.3 Historical values，forecasting values and error analysis of power demand from each model in one region

表4 饱和时间点分析Tab.4 Saturation load year analysis

表5 改进Verhulst 模型预测结果Tab.5 Forecasting results of improved Verhulst model

表6 饱和负荷预测结果Tab.6 Forecasting results of saturation load

5 结论

（1）本文对饱和负荷的判定给出了具体的判定指标集，并形成了一套严谨的分析思路。

（2）本文所提的改进灰色Verhulst 模型有效地改善了预测精度，预测数据符合负荷的增长规律，该方法适用于时间跨度较长的区域级、省市级负荷的饱和预测。

（3）饱和负荷的预测是一项长期的工作，只有不断地累积用电需求与社会经济发展的相关数据，周期地进行滚动性修正预测，才能提高预测模型的适应性，得到更加合理、科学的结论。

[1]崔凯，李敬如，赵彪，等（Cui Kai，Li Jingru，Zhao Biao，et al）. 城市饱和负荷及其预测方法研究（Research on city saturated load and its forecast method）[J]. 电力技术经济（Electric Power Technologic Economics），2008，20（6）：34-38.

[2]崔凯，李敬如，刘海波，等（Cui Kai，Li Jingru，Liu Haibo，et al）. 城市饱和负荷阶段电力规划方法及其在济南电网中的应用（City’s power planning methods at the stage of load saturation and its application in Jinan power grid）[J]. 电网技术（Power System Technology），2007，31（S2）：131-134.

[3]肖峻，杜柏均，耿芳（Xiao Jun，Du Bojun，Geng Fang）. 城市电力负荷饱和分析方法（A method for city power load saturated analyzing）[J]. 电力科学与技术学报（Journal of Electric Power Science and Technology），2009，24（4）：54-58.

[4]崔凯，张丽娟，李敬如，等（Cui Kai，Zhang Lijuan，Li Jingru，et al）. 天津市中心城区饱和负荷分析与预测（Analysis and forecast of saturated load for the central city district of Tianjin）[J]. 电力技术经济（Electric Power Technologic Economics），2008，20（5）：32-36.

[5]王晶， 冯显时， 郭红珍 （Wang Jing，Feng Xianshi，Guo Hongzhen）. 基于蚁群元胞自动机理论的城市饱和负荷预测（Urban load saturation forecast based on ant cellular automata theory）[J]. 中国电力（China Power），2011，44（7）：17-20.

[6]江新琴，李喜兰（Jiang Xinqin，Li Xilan）. 基于空间饱和负荷密度的城市远景饱和负荷预测（City future saturated load forecasting based model of saturated load density）[J]. 福州大学学报：自然科学版（Journal of Fuzhou University：Natural Science），2008，36（4）：532-536.

[7]王芳东，林韩，温步瀛，等（Wang Fangdong，Lin Han，Wen Buying，et al）. 基于模糊综合评价法的电力负荷饱和程度分析（Analysis for the degree of electric load saturation based on fuzzy synthesis evaluation）[J]. 电力与电工（Electric Power and Electrical Engineering），2010，30（3）：1-3.

[8]何永秀，吴良器，戴爱英，等（He Yongxiu，Wu Liangqi，Dai Aiying，et al）. 基于系统动力学与计量经济模型的城市饱和负荷综合预测方法（Combined saturation load forecast model based on system dynamics and econometrics）[J]. 电力需求侧管理（Power Demand Side Management），2010，13（1）：21-25.

[9]张 伏 生，刘 芳，赵 文 彬，等（Zhang Fusheng，Liu Fang，Zhao Wenbin，et al）. 灰色Verhulst 模型在中长期负荷预测中的应用（Application of gray Verhulst model in middle and long term load forecasting）[J]. 电 网 技 术（Power System Technology），2003，27（5）：37-39，81.

[10]王翠茹，孙辰军，杨静，等（Wang Cuiru，Sun Chenjun，Yang Jing，et al）. 改进残差灰色预测模型在负荷预测中的应用 （Application of modified residual error gray prediction model in power load forecasting）[J]. 电 力 系 统 及其自动化学报（Proceedings of the CSU-EPSA），2006，18（1）：86-89.

[11]中华人民共和国国家统计局. 中国统计年鉴[M]. 北京：中国统计出版社，2011.