固体颗粒含量和形状对流体黏度的影响
安卓卿,张延玲,李 琦,郭占成
固体颗粒含量和形状对流体黏度的影响
安卓卿,张延玲,李 琦,郭占成
(北京科技大学钢铁冶金新技术国家重点实验室,北京 100083)
实验采用蓖麻油作为流体,近似于长方体的ABS塑性颗粒及近似于圆盘状的石蜡颗粒作为固体颗粒,以旋转黏度仪为实验仪器,研究固体颗粒含量和形状对流体黏度的影响。结果表明:当蓖麻油中颗粒含量≤10%时,颗粒流体为牛顿流体,当蓖麻油中颗粒含量≥15%时,颗粒流体为非牛顿流体;蓖麻油的黏度随颗粒含量增加而增大,近似于圆盘状的石蜡颗粒比近似于长方体的ABS塑性颗粒对蓖麻油黏度的影响更显著。此外,引入形状系数因子,对Einstein-Roscoe模型进行修正,将修正模型预测结果与实验结果对比分析,验证了修正模型的准确性。
颗粒;流体黏度;旋转黏度计;Einstein-Roscoe修正模型
自然界的物质可分为固、液、气和等离子四态(或4相)。其中,液体气体和等离子体被称为流体,因为它们在不加任何外力的条件下可以变形。当流体中含有大量细小固体颗粒,且流动速度足够大时,固体颗粒的流动类似于流体即固体颗粒可以被视为伪流体(或似流体),与液体、气体和等离子体一起作为流体的流动问题来处理。因而,颗粒流体体系是自然界和工业中的一种最普遍的现象,在无形中影响着人类的生存和生活环境[1]。
在钢铁生产过程中,颗粒流体经常出现在各个流程中,例如高炉渣中出现的高熔点的TiC、TiN及其固溶体Ti(C,N)等高熔点化合物,这些高熔点的物质不溶于渣和铁,因而悬浮、弥散于炉渣中,使炉渣变得粘稠[2]。含有固体颗粒的金属熔体黏度的研究应用也很广泛,如金属泡沫材料和颗粒增强金属复合材料生产等[3−5],以及对于一些金属材料熔体实验结果的解释和金属熔体流动性的模拟也有一定的参考意义[6],此外,陶瓷胶态成型的前提条件中粉体悬浮液的黏度控制也至关重要[7]。因此,研究颗粒对流体黏度的影响机理对实际生产具有广泛的指导意义。此外,煤的利用、石油和天然气的加工、水泥、化肥和各种粉末材料的生产过程,都是在颗粒流体系统中完成的。事实上,各种资源利用、能源转换和环境保护均涉及各种各样的颗粒流体系统。
许多研究学者对颗粒流体黏度的研究表现出了浓厚的兴趣,WU等[8]通过研究含有石蜡颗粒硅油的黏度,对颗粒的尺寸以及体积百分含量对于流体黏度的影响进行了初步研究。王华等[2]用甘油模拟高钛高炉渣,用聚苯硫醚模拟高钛高炉渣中的固体颗粒,模拟分析了不同颗粒尺寸及体积分数的聚苯硫醚对甘油黏度的影响,而关于颗粒形状对于流体黏度的影响还鲜见报道,本研究将在分析颗粒体积百分含量对流体黏度影响的基础上对比分析颗粒形状对流体黏度的影响,并通过对Einstein-Roscoe模型进行修正,引入形状系数影响因子,可以预测颗粒形状对流体黏度的影响,并将修正模型预测结果与实验结果进行对比分析,以验证Einstein-Roscoe修正模型的准确性。
1 实验
1.1 实验仪器与材料
实验采用由本研究团队设计、由东北大学制造的旋转黏度仪进行黏度测试,其示意图如图1所示,原理是:通过两个传感器测量流体作用于转子的黏性力矩来计算流体的黏度,具体计算公式参考文献[9]。此黏度仪由内置传感器、外置传感器、高压罐、连接及冷却系统、转子及样品坩埚、加热元件及炉体组成,可以用于常温下流体黏度的测定,也可用于高温高压下熔体黏度的测定,其内置传感器为大量程传感器,量程为:0~500 Pa·s,外置传感器为小量程传感器,量程为:0~10 Pa·s,本次试验中的颗粒流体黏度小于 10 Pa·s,因此采用外置传感器测量。
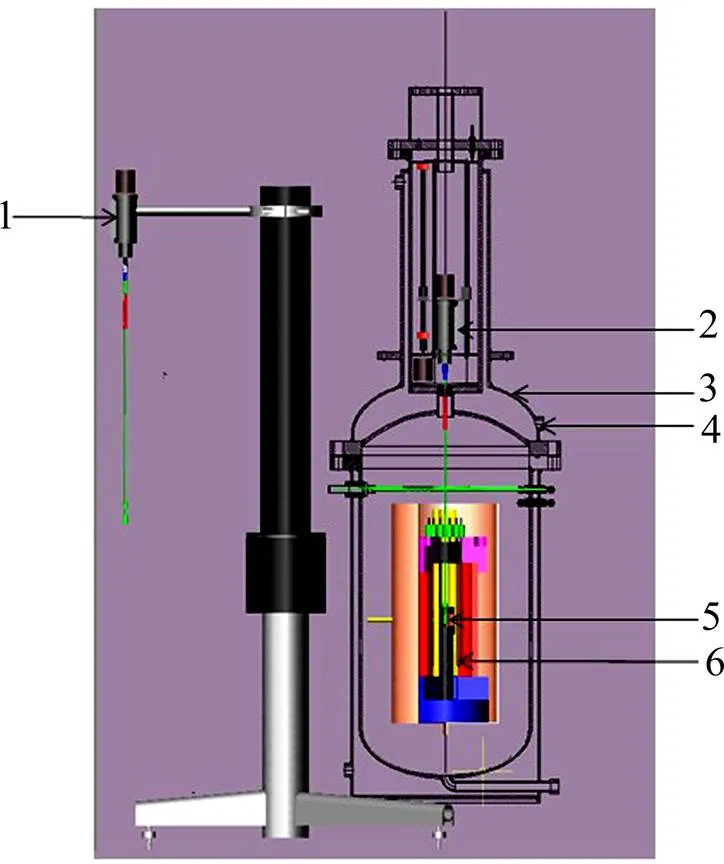
图1 旋转黏度计示意图
1—External sensor; 2—Built-in sensor; 3—High pressure tanks; 4—Link and cooling system; 5—Rotor and crucible; 6—Heating elements and furnace
实验采用蓖麻油(由西陇化工有限公司生产)作为流体,其密度为:0.96×103Kg/m3,采用ABS塑性颗粒(由华南京港塑胶原料有限公司提供)和石蜡颗粒(由中国石油天然气股份有限公司大庆炼化分公司生产)作为固体悬浮颗粒,其密度分别为0.954×103Kg/m3和0.965×103Kg/m3,与蓖麻油的黏度相近,可以有效悬浮在蓖麻油中,其颗粒形状及尺寸(取多个求均值)分别如图2、图3所示。ABS塑性颗粒形状近似为长方体,其尺寸为3.54 mm×3.13 mm×2.86 mm,石蜡颗粒近似于圆盘形状,其周长直径(与颗粒的投影外形周长相等的圆的直径)及高度分别为6.39 mm、3.12 mm。

图2 ABS塑性颗粒

图3 石蜡颗粒
1.2 实验
1.2.1 旋转黏度仪常数标定与仪器稳定性检测
将已知温度的蓖麻油装入特定容器中,在黏度仪中输入温度,同时启动黏度仪,测定蓖麻油的黏度即可得到旋转黏度仪的仪器常数,将得到的常数输入到黏度仪中,标定完成。
由于所采用的黏度仪通常在高温环境下使用,对于将其用于常温下黏度的测定则需要对其稳定性进行检验,故取一定量的蓖麻油,测量蓖麻油(温度为 16.6 ℃)在转速分别为100、150、200、250和300 r/min下的黏度值。
1.2.2 ABS塑性颗粒对蓖麻油黏度的影响
取ABS塑性颗粒的体积分数分别为5%、10%、15%、20%、25%、30%的蓖麻油颗粒流体(总体积 100 mL,温度16.6 ℃),如图4,并分别测其黏度。
1.2.3 石蜡颗粒对蓖麻油黏度的影响
取石蜡颗粒的体积分数分别为5%、10%、15%、20%、25%、30%的蓖麻油颗粒流体(总体积100 mL,温度16.6 ℃),如图5,并分别测其黏度。
2 结果与讨论
2.1 蓖麻油黏度测定
蓖麻油(温度16.6 ℃)在转速分别为100、150、200、250、300 r/min下的黏度值如表1所列:
由于实验设备精度的原因,小数点后第一位为有效数字,剩下的两位可以忽略不计,因此,五种不同的转速下,蓖麻油在温度为16.6 ℃下的黏度值都可以看作是1.6 Pa·s,与文献[10]中给出的蓖麻油黏度值相符,即所测蓖麻油的黏度与转速无关,测试结果符合蓖麻油是牛顿流体的特性,仪器性能稳定,测试误差在可接受的范围内。

图4 ABS塑性颗粒含量分别为5%,10%,15%,20%,25%,30%的颗粒流体

图5 石蜡颗粒含量分别为5%,10%,15%,20%,25%,30%的颗粒流体
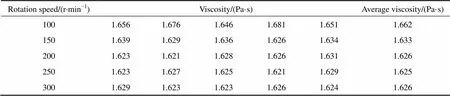
表1 蓖麻油在不同转速下的黏度值
2.2 固体颗粒对流体黏度的影响
2.2.1 颗粒流体的流变特性
含不同体积分数ABS塑性颗粒的蓖麻油在不同转速下的黏度值如图6所示,从图中可以得出,当ABS塑性颗粒含量为5%和10%时,颗粒含量相对较少,颗粒之间距离较大,颗粒相互作用几率小,颗粒之间相互作用可以忽略不计,流体黏度测定值基本不随转速的变化而变化,此时颗粒流体表现出牛顿流体的 特性。
当ABS塑性颗粒含量为15%或高于15%时,流体中颗粒之间距离缩短,颗粒相互作用几率大,颗粒间相互作用不可忽略,随颗粒增多,颗粒之间相互作用增强,此时颗粒流体不再表现出牛顿流体的特性,所测颗粒流体黏度值随转速增加而下降,呈现假塑性流体特征。
2.2.2 固体颗粒的体积分数与形状对流体黏度的影响
图7所示为同一转速下颗粒体积分数与颗粒流体黏度的关系曲线。由图可知,随颗粒体积分数增加,颗粒流体的黏度呈逐步线性增长趋势,对于这种现象可以解释为:对于同种同粒度的固体颗粒,固体颗粒体积分数增大可导致单位体积内固体颗粒相互作用增强,颗粒流体结构强度增大,颗粒流体流动受到的黏滞阻力增大,黏度增大。而对于相同颗粒含量的颗粒流体,含近似于圆盘状石蜡颗粒流体黏度高于含近似于长方体ABS塑性颗粒流体黏度,即近似于圆盘状石蜡颗粒对流体黏度的影响比近似于长方体的ABS塑性颗粒对流体黏度的影响更显著,因此,颗粒形状对流体黏度的影响不可忽略,其具体影响效果将在后续模型修正部分进行详细分析。
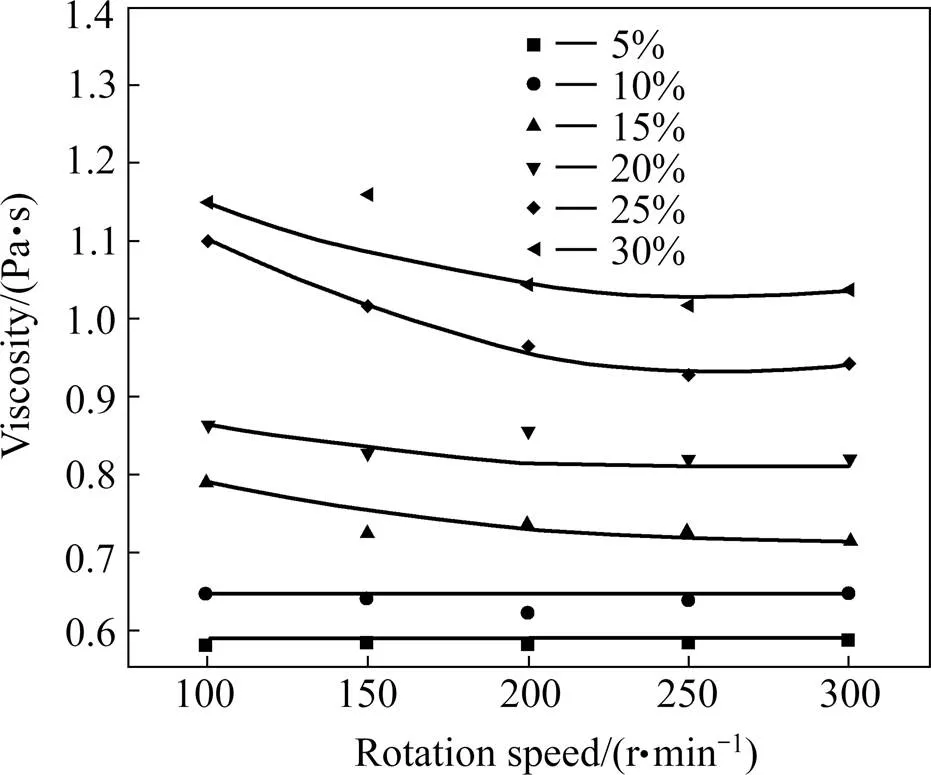
图6 含不同体积分数ABS塑性颗粒的蓖麻油在不同转速下的黏度变化
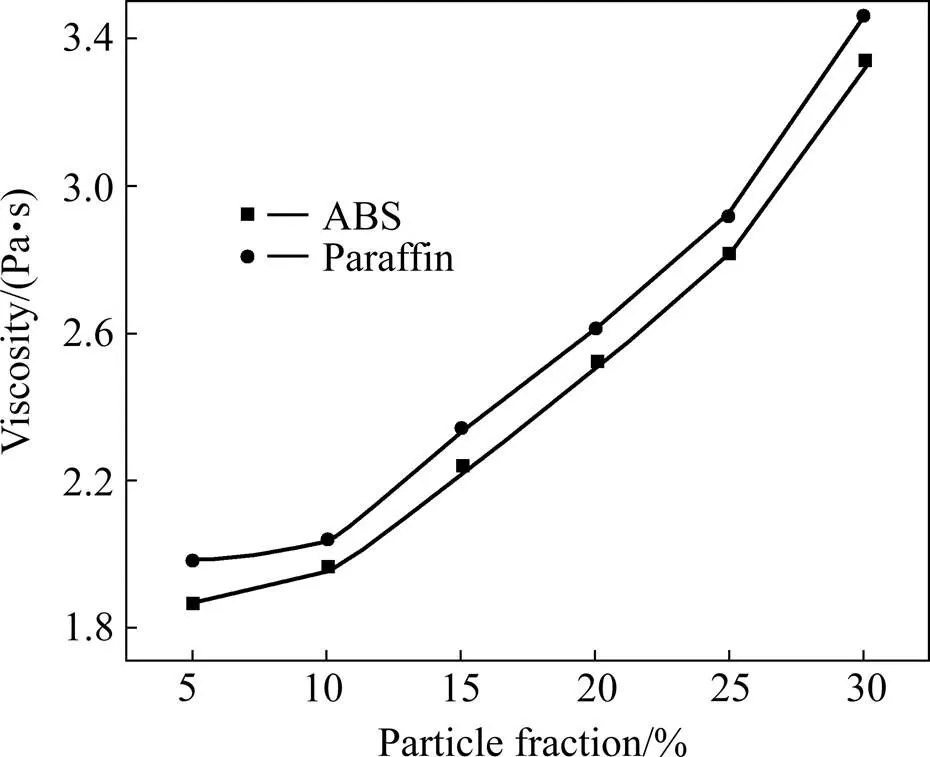
图7 蓖麻油黏度随颗粒含量的变化
2.3 Einstein-Roscoe模型的修正及与实验数据的验证分析
对于含颗粒流体黏度的预测模型有很多,其中,被广泛应用的是Einstein模型,对于低浓度的硬球颗粒流体,Einstein假设硬球颗粒半径远小于测量装置的半径,远大于溶剂分子半径,硬球颗粒之间没有相互作用,硬球颗粒流体处于层流流动,由此给出了含颗粒流体的黏度与颗粒体积分数之间的关系[11−12]:
=0(1+) (1)
式中:和0分别为颗粒流体和不含颗粒的流体黏度;为颗粒的百分含量;为常数值,与颗粒的形状及可变形性有关,在Einstein模型中颗粒为硬球形,为2.5[13−14]。
Einstein模型没有考虑颗粒间的相互作用,因此只能用于低浓度的颗粒流体。Roscoe在Einstein模型的基础上,假定球形颗粒尺寸各不相同,在全浓度范围内得到公式[15]:
=0(1−)−2.5(2)
当球形颗粒体积分数较大且颗粒尺寸相同时,Roscoe在Vand的理论基础上将公式(2)优化为:
=0(1−1.35)−2.5(3)
Roscoe在公式(2)和公式(3)的推导过程中将颗粒含量作为主要因素进行推导计算并未考虑颗粒形状的影响因素,而在Einstein的公式(1)中形状因素的影响作用不可忽略,并在公式(1)用表示颗粒可变形性和形状对颗粒流体黏度的影响,因此本研究将重点研究颗粒形状对流体黏度的影响,将形状系数引入Einstein-Roscoe模型进行深入分析。本研究中同粒度石蜡颗粒和ABS塑性颗粒的大小不完全相同,因此,选用公式(2)进行修正。实验在室温下进行,ABS塑形颗粒和石蜡颗粒可变形性均可忽略不计,因此本文将作为与颗粒形状有关的系数引入公式(2),即
=0(1−)−2.5(4)
颗粒形状是颗粒的一个重要几何特征,影响着粉体颗粒的一些重要性质,如粉体的比表面积、流动性、包装性、堆积性、附着性、流体透过阻力、气体透过性、颗粒与流体相互作用、化学反应活性和烧结强度等[1, 16]。对于颗粒形状的描述参数中,球形度(c)是应用较广泛的参数,用于衡量一个物体的球形化程 度[17]。本研究中,将球形度作为颗粒的主要形状系数,即=文献[18]中给出的球形度参考值如表2所列。
根据图2中ABS塑性颗粒的形状近似于长方体,长:宽:高≈1:1:1,则ABS取0.81;图3中石蜡颗粒的形状近似于圆盘状,高:直径≈1:2则石蜡取0.83.为了验证Einstein-Roscoe修正模型的准确性,将ABS和石蜡带入Einstein-Roscoe修正模型公式(4)计算黏度值并与实验测得黏度值进行比较,结果如图8所示。

表2 简单几何形状颗粒的球形度

图8 (a)含ABS塑性颗粒流体表观黏度的模型预测值与实验值对比;(b)含石蜡颗粒流体表观黏度的模型预测值与实验值对比
由图8可以看出,Einstein-Roscoe修正模型预测结果与实验测得结果趋势基本一致,说明在实验浓度范围内,引入形状系数后的Einstein-Roscoe修正模型能够对固体颗粒含量和形状对流体黏度的影响进行预测。需要指出的是,在10%~25%的浓度范围内,Einstein-Roscoe修正模型预测误差较小,而固体颗粒含量较低(5%)、或较高(30%)时,预测结果与实验结果偏差相对较大。说明过低或过高颗粒浓度分布情况下,颗粒之间相互作用及可变形性的影响不容忽略,Einstein-Roscoe模型需要进一步修正。
低噪声放大器选用飞利浦的BGA2001,它是一款可应用于低电压情况的单片微波集成放大器,最大电源电压为4.5 V;在1~1.6 GHz频段内,即包含卫星导航信号的工作频段内,增益高达20 dB,噪声系数低至1.3 dB。图2是设计的低噪放电路。
3 结论
1) 当颗粒流体中固体颗粒含量≤10%时,颗粒流体为牛顿流体,当固体颗粒含量≥15%时,颗粒流体为非牛顿流体,表现出假塑性流体的特征。
2) 颗粒流体的黏度随固体颗粒含量增加而增大,近似圆盘状颗粒比近似长方体颗粒对流体黏度的影响更大。
3) 对于Einstein-Roscoe模型进行修正,引入形状系数即=0(1−)−2.5,根据颗粒形状选择相应形状系数,Einstein-Roscoe修正模型能够对固体颗粒含量和形状对流体黏度的影响进行预测。
REFERENCES
[1] 叶 菁. 粉体科学与工程基础[M]. 北京: 科学出版社, 2009: 69−70. YE Qing. Fundamentals of Powder Science and Technology [M]. Beijing: Science Press, 2009: 69−70.
[2] 王 华. 高钛高炉渣变稠规律的实验研究[D]. 重庆: 重庆大学, 2013: 4/5, 11−20.WANGHua. Experimental study on thickening mechanism of blast furnace slag bearing titanium [D]. Chongqing: Chongqing University, 2013: 4/5, 11−20.
[3] RAY S. Synthesis of cast metal matrix particulate composites [J]. Journal of Materials Science, 1993, 28(20): 5397−5413.
[4] HASHIM J. The production of cast metal matrix composite by a modified stir casting method [J]. Jurnal Teknologi, 2001, 35(A): 9−20.
[5] KAPTAY G. Interfacial criteria for producing metal matrix composites and ceramic particle stabilized metallic foams [J]. Mater Sci Forum, 2003: 414−415.
[6] BORIN D, ODENBACH S. Viscosity of liquid metal suspensions-experimental approaches and open issues [J]. The European Physical Journal Special Topics, 2013, 220(1): 101−110.
[7] 罗玉林, 王小锋, 彭超群, 等. 煅烧预处理对胶态成型用BeO粉体性能的影响[J]. 粉末冶金材料科学与工程. 2010, 15(2): 151−156. LUO Yu-lin, WANG Xiao-feng, PENG Chao-qun, et al. Effects of calcination pretreatment on properties of BeO powder for colloidal processing [J]. Materials Science and Engineering of Powder Metallurgy, 2010, 15(2): 151−156.
[8] WU L S, MATTIAS E K, Minho S, et al. The effect of solid particles on liquid viscosity [J]. Steel research int, 2011, 82(4): 388−397
[9] 陈惠钊. 黏度测量[M]. 北京: 中国计量出版社, 2002, 56−60. CHEN Hui-zhao. Viscosity Measurement [M]. Beijing: China Metrology Press, 2002, 56−60.
[10] 金 叶, 刘雪芹, 彭川黔, 等.蓖麻油粘滞系数公origin拟合[J]. 大学物理实验, 2012, 25(1): 58−60. JIN Ye, LIU Xue-qin, PENG Chuan-qian, et al. Fitting time functions of castor oil viscous coefficient by origin [J]. Physical Experiment of College, 2012, 25(1): 58−60.
[11] EINSTEIN A. Effect of suspended rigid spheres on viscosity [J]. Ann Phys 1906, 19: 289−306.
[12] EINSTEIN A. Berichtigung [J]. Ann Phys, 1911, 34: 591−592.
[13] SZABO P, HANSEN R. Viscosity of suspensions and finite size effects [J]. Annu Trans Nordic Rheol Soc, 2008: 16−17.
[14] SZABO P, HANSEN R. Viscosity of suspensions. Finite size effects and polydispersity [C]. In 18th Nordic Rheology Conference: 119−120.
[15] ROSCOE R. The viscosity of suspensions of rigid spheres [J]. British Journal of Applied Physics, 1952, 3(8): 267−269.
[16] 陶珍东. 粉体工程与设备[M]. 北京: 化学工业出版社, 2009, 7−8. TAO Zhen-dong. Powder Technology and Equipment [M]. Beijing: Chemical Industry Press, 2009: 7−8.
[17] 刘梅芳, 陈素芬, 刘一杨, 等. 厚壁空心微球的球形度和壁厚均匀性的表征研究[J]. 强激光与粒子束, 2014, 26(2): 0220171−0220175. LIU Mei-fang, CHEN Su-feng, LIU Yi-yang, et al. Characterization of sphericity and wall thickness uniformity of thick-walled hollow microspheres [J].High Power Laser and Particle Beams, 2014, 26(2): 0220171−0220175.
[18] 谢洪勇. 粉体力学与工程[M]. 北京: 化学工业出版社, 2007: 8−9. XIE Hong-yong. Powder Mechanics and Engineering [M]. Beijing: Chemical Industry Press, 2007: 8−9.
(编辑 高海燕)
Effect of particle fraction and shape on fluid viscosity
AN Zhuo-qing, ZHANG Yan-lin, LI Qi, GUO Zhan-cheng
(State Key Laboratory of Advanced Metallurgy, University of Science and Technology Beijing, Beijing 100083, China)
The viscosity of fluids containing particles was measured by rotation viscometer, during which castor oil was used as fluid, ABS plastic pellets and flaky paraffin acted as solid particles .The results show that when particle fraction is lower than 10%, the fluids still behave as Newtonian flow, while in the case of larger than 15% the fluids exhibit non-Newtonian flow features; as well with increasing particle fraction the viscosity of castor oil increases and the effect of flaky particles is greater than ABS plastic pellets under same situation. In addition, the Einstein-Roscoe model was modified by introducing a shape factor and used to pre-estimate the viscosities which was used to compare with the experimental result. And the comparison result proves that thus modified Einstein-Roscoe model is good to pre-estimate the viscosity.
particles; fluid viscosity; rotation viscometer; the modified Einstein-Roscoe model
TB302
A
1673-0224(2015)1-46-07
国家自然科学基金资助项目(No.51234001)
2014-03-10;
2014-09-29
张延玲,副教授,博士。电话:010-82375191;E-mail: zhangyanling@metall.ustb.edu.cn

