基于约束逼近投影变换的全景图像拼接方法

余清洲,陈水利,蔡　国榕,苏松志，吴云东

(1.厦门市无人机遥感应用工程技术研究中心，福建 厦门 361021；2.集美大学理学院，福建 厦门 361021；

3.集美大学诚毅学院，福建 厦门 361021；4.集美大学计算机工程学院，福建 厦门 361021；

5.厦门大学信息科学与技术学院，福建 厦门 361005)



基于约束逼近投影变换的全景图像拼接方法

余清洲1,2,陈水利1,3,蔡国榕1,4,苏松志5，吴云东1,4

(1.厦门市无人机遥感应用工程技术研究中心，福建 厦门 361021；2.集美大学理学院，福建 厦门 361021；

3.集美大学诚毅学院，福建 厦门 361021；4.集美大学计算机工程学院，福建 厦门 361021；

5.厦门大学信息科学与技术学院，福建 厦门 361005)

[摘要]全景图像拼接算法是遥感信息处理、图像处理等领域的研究热点.基于逼近投影变换的算法对低空遥感图像拼接有较好的效果，但对于远离参考图像的矩形块会出现较大的畸变并且拼接缝周边会出现大量的形变、鬼影等现象.为此，在逼近投影变换的基础上，提出一种基于光束平差与投影变换相结合的图像拼接策略，目的是通过约束变换总误差来减少畸变现象.针对低空航拍图像的实验结果表明，与传统拼接算法相比，新方法减少了图像中的鬼影和模糊，且避免了建筑物、道路等地物的畸变现象.

[关键词]投影；变换；动态直接线性变化；逼近投影变换算法；光束平差法

0引言

全景图像拼接是当前遥感信息工程、计算机视觉、图像处理等领域的重要研究课题.目前大多数方法以特征点为基础，其基本流程包括：估计图像的变换矩阵，使重叠的区域对齐，然后使对齐配准的图像合并到一个共同的图像坐标系上.在文献[1]中可以找到一系列关于图像自动拼接的优秀算法.当前比较流行的合成图像拼接技术中，最主要的有基于Graph Cut算法的缝切割方法[2-3]和先进的像素融合技术，如拉普拉斯金字塔融合[4]和泊松图像融合[5]，这样可以减少由于无法对齐而导致的模糊.

在图像对齐方面，近年来出现很多优秀算法，如：对于图像中只有局部配准误差的情况，文献[6]提出了一种保护内容的变换算法(Content-Preserving Warps,CPW)，将图像分割为固定网格，通过优化每个网格中基于局部对齐的数据项和基于全局相似矩阵的平滑项所建立的能量函数得到最优的单应矩阵；对于具有两类较大几何变换的图像，如远景与近景情况，文献[7]提出了一种双单应性变换算法(Dual-Homography Warping，DHW)，采用聚类算法将特征点分为近景与远景类，并确定相应的单应矩阵，最终在局部使用加权的单应矩阵变换图像；对于更复杂的拍摄环境下(不仅只有近景与远景)的变换模型，文献[8]提出了一种多个平滑变化的仿射变换算法(Smoothly Varying Affine，SVA)，分别在两幅图像中提取一定数量的特征点，建立混合高斯模型，利用EM算法得到光滑变化的局部仿射变换参数；对于建立多个复杂几何模型依然无法很好对齐的图像，文献[9]提出了缝驱动拼接算法(Seam-Driven Image Stitching,SEAM)，对同一组图像进行多次匹配拼接，寻找每组拼接结果的拼接缝并计算对应的能量函数，使用损失函数值最小的一组对齐图像作为最终拼接结果.

然而，如果提供的图像数据不够理想，特别是遥感图像中的复杂环境，存在不同的高程信息，每个区域对应不同单应性，只简单使用一个或几个单应性矩阵很难完整表达图像之间的几何关系，使用以上方法[6-9]将无法得到令人满意的拼接结果.为了使最后生成的全景图没有太大的畸变保证建筑物的几何结构符合实际，又要对图像的局部区域进行精确配准，保证没有模糊及鬼影现象，本文仔细分析了光束平差法(Bundle Adjustment，BA)对全局配准的约束效果和逼近投影变换算法[10](As-Projective-As-Possible Warp， APAP)在图像局部配准上的优秀特性，将两种算法结合起来以解决无人机遥感图像的拼接问题.

1逼近投影变换算法

1.1　投影变换基本原理

(1)

(2)

1.2　动态直接线性变换

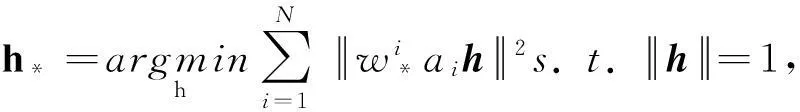
(3)

(4)

σ是一个标量.由式(4)可以知道，与点p*越接近的点权值更大.称其为动态直接线性变换算法.将式(3)重新书写为：

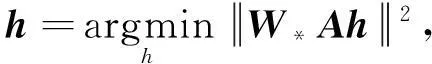
(5)

2全景图像拼接

2.1　光束平差法

在进行全景图像的拼接时，累积误差将会导致图像的两端产生过度的变形，这将产生不理想的结果.光束平差法[11]就是保证大量图像在进行拼接时，保持在同样的几何结构上，避免图像的过分失真.

(6)

2.2　约束逼近投影变换算法

当待拼接的图像是无人机遥感图像时，由于飞机在一个固定的高度基本保持平稳的飞行状态，所得到的图像近似接近正摄影图像，图像间具有良好的几何关系，在没有大的旋转、缩放的情况下，只需要进行简单的平移和微调，就可以得到相对满意的拼接结果.在拼接的过程中应尽量减少道路、建筑物等图像中目标的失真.使用经过全局光束平差法修正过的单应矩阵可以约束图像的整体几何结构.但这也将不可避免地导致图像局部匹配的不精确，从而导致较明显的鬼影和模糊现象.为此本文提出了一种基于光束平差法优化的逼近投影变换算法.

如图2a所示，根据公式(9)，为了使全局的误差函数最小，多个点与点之间将无法完全对齐，每个点都做出了牺牲.当使用平均值融合算法得到全景图像IPorig时，由于同一对应点出现在了画布的不同位置，而产生了鬼影和模糊现象.如图2b所示，虽然有鬼影现象，但总会有一点相对于其他的对应点的强度更大.图2中，使用实心的点表示强度最大的点，空心的点表示被融合算法弱化掉的点，继续使用高斯平滑可使这一现象更明显.

本算法的主要流程如下：

1)使用傅里叶梅林算法，计算图像间的拓扑关系，在图像序列中选出一张参考图像IR;

3实验结果分析

3.1　参数设置与运行时间

实验使用CPU为IntelCore2E7500 ，内存3G，系统为Window7 32位的普通计算机.在进行逼近投影变换算法时，采用的是作者提供的开源代码[14]，而光束平差法是基于谷歌的开源代码Ceressolver库函数[15]进行编写的.

本研究采用的实验数据为2013年在福建省龙岩市才溪镇拍摄的无人机遥感图像，降采样后的分辨率为983×653.对每张图像选取的特征点数为800个.在对图像进行分块时，设置C1=50,C2=50，这样既能得到最佳的拼接效果，又能减少程序的内存消耗.

实验中采用了多条航带，每条航带抽取5到6张遥感图像进行拼接，由于计算机的计算时间具有随机性，故对同一个拼接任务进行了多次计算.包括预处理阶段在内，全部计算时间平均小于4min，每一张图像，特征点的提取和匹配使用时间平均小于15s，光束平差法的时间平均小于5s，即每张图像的动态直接线性变换计算时间平均小于20s.

3.2　实验结果分析

图3为一组具有不同高程信息的航拍图像全景拼接的实验结果，其中第一行为APAP算法的结果，第二行为光束平差法的拼接结果，第三行为本文算法的拼接结果.在第一列的全景图中可以看到APAP算法没有明显的视差现象，但全局发生了较大的扭曲，特别是第一行中蓝色椭圆圈出的局部区域可以清楚地看到全景图像底部和右部边缘出现严重变形，道路和建筑物等也发生较大扭曲；光束平差法保证了全景图像整体几何关系的稳定，但从放大图像中可以看到，模糊与鬼影现象较明显，特别是房屋与树木等较高程的区域；本文算法与光束平差法一样很好地保证了全局的几何结构，且在红色矩形圈出的放大图像中，房屋和道路的拼接结果准确清晰，肉眼几乎无法发现模糊和鬼影.

在灾害应急及虚拟现实等实际应用中，具有较大几何畸变的图像没有利用价值，故在进行误差分析时，对于APAP算法不予考虑.只使用光束平差法与本文的约束逼近投影变换算法进行比较.

从表1可以看出，与传统的光束平差法相比，本文算法匹配精度得到了很大提高，每个像素的精准度可以提高2到4个像素，大大减轻了视差现象.

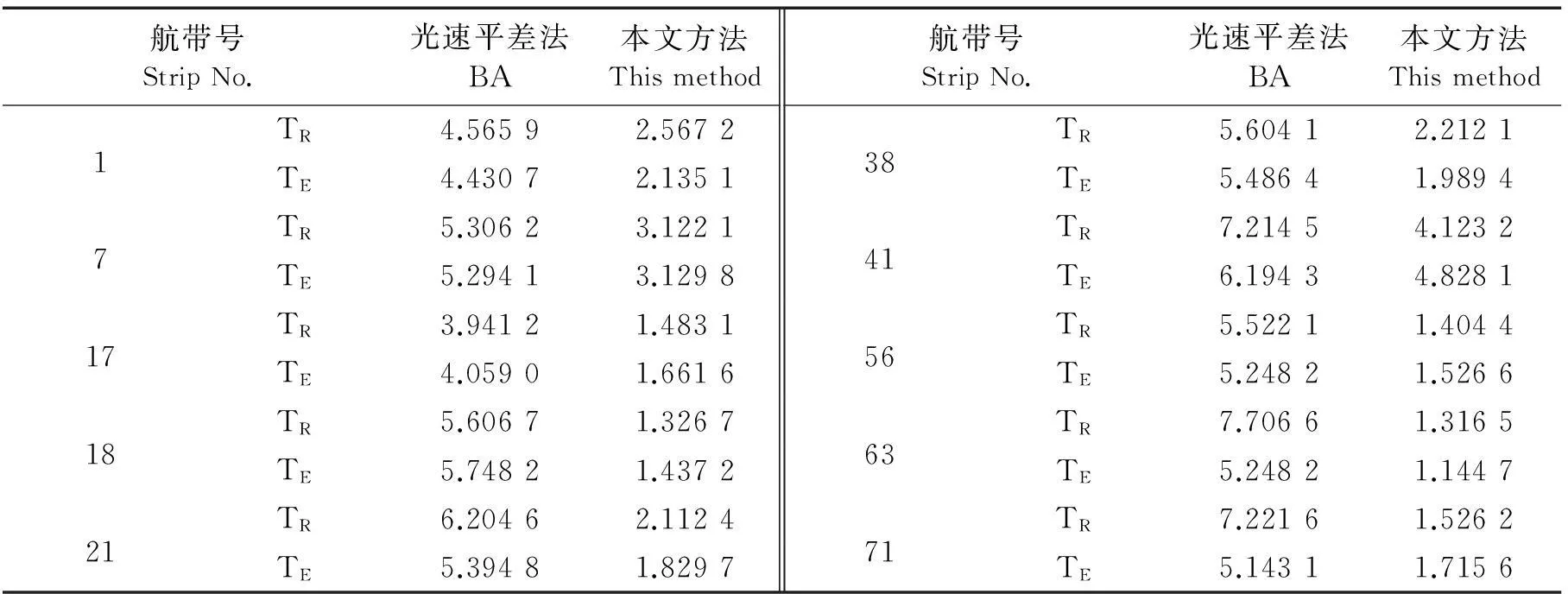
表1　误差检测

4结束语

本文提出了一种针对遥感图像的全景拼接算法，它充分发挥了光束平差法和逼近投影变换算法各自的优势，与传统算法相比，减少了视差的出现，并避免了道路和建筑物的扭曲.本文算法具有较大的灵活性，在得到最终拼接结果后，可以根据图像的质量，继续采用结果图作为参考帧迭代进行逼近投影变换，以达到预期的目标.但这个算法依赖于光束平差法的拼接质量，若初始的拼接效果不理想，在后续的二次配准中将影响图像的拼接结果.今后将进行最优拼接缝的研究，以消除依然存在的部分模糊现象.

[参考文献]

[1]SZELISKIR.Image alignment and stitching:a tutorial[J].Foundations and Trendsin Computer Graphics and Vision,2006,2(1):1-104.

[2]AGARWALA A,DONTCHEVA M,AGRAWALA M,et al.Interactive Digital Photomontage[J].ACM Trans Graph,2004,23(3):294-302.

[3]EDEN A,UYTTENDAELE M,SZELISKIR.Seamless image stitching of scenes with large motions and exposure differences[C]//Proceeding of Computer Society Conference on Computer Vision and Pattern Recognition.New York:IEEE,2006,2:2498-2505.

[4]BURT P J,ADELSON E H.A multiresolution spline with application to image mosaics[J].ACM Transactions on Graphics(TOG),1983,2(4):217-236.

[5]PURT P J,ADELSONM,BLAKE A.Poisson image editing[J].ACM Transactions on Graphics (TOG)，2003,22(3):313-318..

[6]LIU F,GLEICHER M,JIN H,et al.Content-preserving warps for 3D video stabilization[J].ACM Transactions on Graphics(TOG),2009,28(3):44.

[7]GAO J,KIM S J,BROWN M S.Constructing image panoramas using dual-homography warping[C]//2011 IEEE Conference on Computer Vision and Pattern Recognition.Colorado,USA:IEEE,2011:49-56.

[8]LIN W Y,LIU S,MATSUSHITA Y,et al.Smoothly varying affine stitching[C]//Proceeding of Computer Society Conference on Computer Vision and Pattern Recognition.Colorado,USA:IEEE,2011:345-352.

[9]GAO J,LI Y,CHINT J,et al.Seam-Driven Image Stitching[C]//Eurographics 2013-Short Papers.Girona,Spain:The Eurographics Association,2013:45-48.

[10]ZARAGOZA J,CHIN T J,BROWN M S,et al.As-Projective-As-Possible image stitching with moving DLT[C]//Proceeding of Computer Society Conference on Computer Vision and Pattern Recognition.Ohio,USA:IEEE,2013:2339-2346.

[11]AGARWAL S,SNAVELY N,SEITZ S M,et al.Bundle adjustment in the large[M]//Computer Vision-ECCV.Berlin :Springer Heidelberg,2010:29-42.

[12]BROWN M,LOWED G.Automatic panoramic image stitching using invariant features[J].International Journal of Computer Vision,2007,74(1):59-73.

[13]REDDY B S,CHATTERJIB N.An FFT-based technique for translation,rotation,and scale-invariant image registration[J].IEEE Transactions on Image Processing,1996,5(8):1266-1271.

[14]JULIO ZARAGOZA.MDLT[EB/OL].(2014-04-08)[2014-10-31].http://cs.adelaide.edu.au/~jzaragoza/doku.php?id=mdlt.

[15]AGARWAL S,MIERLE K.Ceres solver[EB/OL].(2014-06-09)[2014-10-31].https://code.google.com/p/ceres-solver/.

(责任编辑朱雪莲英文审校黄振坤)

Panoramic Image Stitching Based on ConstraintAs-Projective-As-Possible TransformYU Qing-zhou1,2,CHEN Shui-li1，3，CAI Guo-rong1,4,SU Song-zhi5,WU Yun-dong1,4

(1.Xiamen UAVRS Application Engineering Technology Research Center,Xiamen 361021,China;

2.School of Science,Jimei University,Xiamen 361021,China;3.Chengyi College,Jimei University,

Xiamen 361021,China;4.School of Computer Engineering,Jimei University,Xiamen 361021,China;

5.School of Information Science and Technology,Xiamen University,Xiamen 361005,China)

Abstract:Panoramic image mosaic algorithm is a hot topic in the fields of remote sensing and image processing.State-of-the-art such as As-Projective-As-Possible (APAP) warp is efficient in low altitude remote sensing image mosaic.However,in APAP related algorithms,the rectangular block away from the reference image and seams suffer from large scale deformation and parallax,respectively.Therefore,in this paper,a novel algorithm that is based on the as-projective-as-possible warps and bundle adjustment is proposed.The purpose is to control the total transform error,thus to reduce image distortion.Experimental results conducted on low-altitude aerial images show that the proposed method reduces the phenomenon of ghosting and blurring.Moreover,the distortions of buildings and roads have been alleviated.

Key words:Projective；Warp;Moving DLT;As-Projective-As-Possible Warps;Bundle Adjustment

[中图分类号]TP 391.41

[文献标志码]A

[文章编号]1007-7405(2015)06-0463-07

[作者简介]余清洲(1990—)，男,硕士生，主要研究方向为图像处理与模式识别.通信作者：陈水利(1956—)，男，教授，从事模糊数学及其应用、遥感影像信息处理等方面研究，E-mail:sgzx@jmu.edu.cn

[基金项目]国家自然科学基金项目(61202143)；国家科技支撑计划项目(201309110001)；863项目子课题(2012AA12A208-06)；国家博士后基金项目(2014M561090)；福建省自然科学基金项目(2013J01245,2012J01013)；福建省科技厅专项(JK2012025)；福建省科技计划重点项目(2014H0034)

[收稿日期]2015-03-31[修回日期]2015-04-26