基于两阶段求解的动态车辆路径问题研究
陈 诚,邱荣祖
(福建农林大学交通与土木工程学院,福建 福州 350002)
基于两阶段求解的动态车辆路径问题研究
陈诚,邱荣祖
(福建农林大学交通与土木工程学院,福建 福州 350002)
[摘要]采用两阶段求解思想,通过设置定时间隔,将动态信息转化成静态信息,从而实现对动态车辆路径问题的求解.分别建立了初始优化和实时优化阶段的数学模型,以节约算法解为初始解,利用禁忌搜索算法完成初始优化阶段的车辆路径问题求解;在实时优化阶段,分别对节约算法和禁忌搜索算法进行适当修正后再进行求解.利用数值测试实验对客户不同地理位置分布下定时间隔的设置进行测试分析.结果表明,该算法简单明了,易于实现.此外,客户的地理位置分布不同,对定时间隔的敏感性也不同,混合分布最为敏感,其次是随机分布,集聚分布最不敏感;最后,给出了相应的累计服务客户数量曲线,并结合车辆总行驶距离,明确了不同客户位置分布下的较优定时间隔设置.
[关键词]动态车辆问题;两阶段求解;定时间隔;禁忌搜索
0引言
车辆路径问题(vehicle routing problem,VRP)自1959年Dantzig和Ramser提出后[1],成为了国内外众多学者研究的热点.在过去几十年中,对该问题的研究取得了丰富的研究成果.然而在这些研究成果中,大多是在静态的环境下进行的,即静态VRP(Vehicle Routing Problem),但这与现实环境动态变化的特点不相符.因此,为了更好地解决实际问题,有必要对动态VRP进行研究.
对动态车辆路径问题研究,最早可以追溯到20世纪70年代Wilson对动态dial-a-ride问题的研究[2].动态车辆路径问题的一大特征在于与问题相关的信息是随时间的推移而出现或发生变化的.这一特征表明了所研究对象的复杂性很大一部分取决于所考虑的动态因素数目的多寡.若综合考虑各种动态信息对所研究问题的影响,将会使问题变得十分复杂、难解.大多数学者在研究中往往只考虑少数几种动态因素对问题的影响.例如,Gendrea[3]等研究了客户请求新增的实时车辆调度问题;Zhu[4]等研究了车辆旅行时间变化的动态车辆调度问题,建立了问题的数学模型,并为其设计了爬山算法;Haghani[5]等研究了考虑即时服务要求和时变车辆旅行时间的动态车辆路径问题[2];Azi[6]等研究了客户需求动态变化的车辆路径问题,决策变量包括是否接受客户请求.动态车辆路径问题的求解难度源于对动态信息的处理,有些学者采用判断准则,将新客户添加到已经制定的调度方案中[7-8],有些学者采用现代优化算法重新进行整个调度方案的优化[9-10],基本思路都是将动态信息转换成静态信息再进行路径构造,并分别提出了“时间轴”和“时间片”的概念,以明确动态信息处理的时间间隔.可以说时间间隔的设定是动态信息分批处理过程中的重要参数,因为过短的时间间隔会增加求解负担,而过长的时间间隔既不利于客户的实时响应,也会增加配送成本,在已有研究中缺乏该参数对求解结果影响的研究.
本文通过预优化和实时优化相结合的方法研究动态车辆路径问题,设置时间间隔及关键点将动态信息静态化,分别建立了两阶段的数学模型;采用节约算法构造初始解,禁忌搜索算法寻优的方法进行预优化阶段车辆路径问题的求解,在仿真实验阶段,采用随机分布、集聚分布和混合分布三种不同分布地理位置的客户数据进行实验,实验结果表明本文提出的求解方法的可行性与合理性,同时还分析了定时间隔设置对求解结果的影响,在考虑客户服务水平的前提下,明确了客户地理位置不同分布下定时间隔的优化设置.
1动态车辆路径问题描述
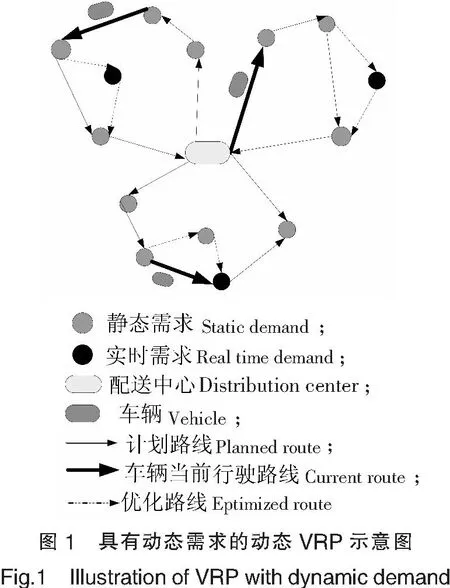
本文研究的动态车辆路径问题可以描述如下:某一配送中心有K辆车型相同且最大负载能力均为Qk的车辆,中心每天需满足客户的配送需求,客户i的位置及其需求量qi的出现事先未知,每个客户只能被一辆车访问一次,车辆完成运输任务后需回到配送中心;伴随时间的改变,客户需求可能发生动态变化,配送中心需要进行合理的车辆调度以适应客户及其需求的动态变化.如图1所示,配送中心首先为车辆规划一条路线,但是在车辆运行过程中,由于客户的动态变化,车辆的运行路线也将发生相应的变化.本文中考虑的客户动态变化主要考虑客户需求的变化.
2求解思路
对于车辆路径问题中的动态因素,主要求解思路之一是将动态因素转变成静态因素再进行求解[10].通过定时间隔和关键点的设置将动态因素静态化,对静态化后车辆路径问题进行多次实时求解,从而实现对动态车辆路径问题的实时优化,即两阶段求解,也是目前的主流求解思路[11-13].
2.1 定时间隔
把按照一定原则划分的小时间段称为定时间隔,每个间隔结束的时刻记为对应的时刻1,…,n(初始优化阶段记为时刻0).因此在初始时刻对已知客户按静态车辆路径问题进行优化,车辆开始按初始优化结果开始运行,之后在每个定时间隔结束时进行实时优化,在下一个定时间隔开始时,所有车辆按实时优化结果继续运行.
2.2 关键点
在实时优化阶段,执行初始行驶计划的车辆已经离开配送中心,可能已经满足部分客户的需求,此时每辆车的剩余载重都不同,且车辆所在位置不同,因此将在定时间隔结束时,已派出的车辆所在的位置定义为关键点[16].关键点只发出对应的车辆,而不接受其他车辆的访问,于是实时优化阶段的车辆路径问题可以看成是多配送中心车辆路径问题,限制位于关键点的虚拟配送中心发且只能发出一辆车,容量为定时间隔结束时的剩余容量,且最后必须返回配送中心.
本文动态车辆路径问题的具体求解思路如图2所示.

3数学模型
对于动态车辆路径问题,分别建立其初始优化阶段和实时优化阶段的数学模型.模型中:0为配送中心;L为静态客户集合;K0为初始车辆集合;K1为定时间隔结束时已派出车辆集合;N为车辆路径中仍未被服务的对象和新增的客户集合;T为实时优化阶段增派的车辆数;M表示关键点集合;Qk为车辆k的最大载质量;qi为客户i的需求量;Qik为车辆k从需求点i出发时的载质量,若车辆k从配送中心出发则Q0k=Qk;cij为客户i与客户j之间的距离;xijk为0-1变量,若车辆k从客户i行驶至客户,则等于1,否则等于0;yik为0-1变量,若客户i由车辆k服务j,则等于1,否则等于0;
3.1 初始优化阶段数学模型
总费用最小的目标函数如式(1)所示,表示车辆总行驶路径最短.

(1)
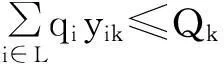
3.2 实时优化阶段数学模型
目标函数如式(2)所示,保证在满足当前所有客户需求的前提下,从关键点及配送中心出发的车辆,行驶的总路径最短.

(2)

4动态车辆路径问题两阶段求解算法
以上设计的两阶段求解策略中涉及了两个阶段不同的路径问题的求解,第一阶段即静态车辆路径问题的求解,第二阶段类似于多配送中心车辆路径问题的求解,而禁忌搜索算法在快速求解车辆路径问题上有着十分明显的优势,故本研究采用禁忌搜索算法进行两个阶段的车辆路径问题的求解.
4.1 初始优化阶段禁忌搜索算法设计
初始优化阶段的车辆路径问题为静态车辆路径问题,本文采用的禁忌搜索求解算法中的主要要素及参数设置如下:
1)解的表示采用客户直接排列的方法;2)初始解的生成方法采用节约算法进行;3)将目标函数值作为解的评价标准;4)同时采用任意两点交换和将一点插入至另一点后的方法进行邻域构造;5)将每一次迭代得到的最好解作为禁忌对象放入禁忌表中;6)根据问题的规模选取一个固定的长度为禁忌长度;7)终止准则采取给定一个最大迭代步数.
4.2 实时优化阶段的禁忌搜索算法设计
实时优化阶段的车辆路径问题的禁忌搜索算法求解流程及主要参数同初始优化阶段,但关键点(虚拟配送中心)做如下处理:
1)配送中心0至虚拟配送中心的距离设置为零,虚拟配送中心发出车辆的容量为原车辆容量减去关键点前路线上所有客户的需求量之和.
2)节约算法阶段,首先将虚拟配送中心的一端和配送中心相连,这样若虚拟配送中心的另一端和客户端相连后,虚拟配送中心就成为了路线的内点,不能再和其他点相连;其次将两个虚拟配送中心的节约值设为零,保证两个虚拟配送中心不会相连.
3)禁忌搜索算法编码阶段,虚拟配送中心按客户点方式直接排列;解码阶段,按客户排列顺序将客户加入到路线中,遇到虚拟配送中心则重新开始一条新路线,从而保证虚拟配送中心发且只能发出一辆车,而不能接受其他车辆的访问.
5仿真实验与讨论
为了评价客户不同地理位置分布对求解结果的影响,采用soloman的标准测试数据(R101,C101,RC101),因时间窗不在本文研究范围内,故去掉测试数据中的时间窗数据;但是因需采集定时间隔结束关键点的信息,因此保留客户服务时间数据.三类数据中的地理位置均在100×100的欧几里得平面坐标系中产生,其中,R类数据中的客户地理位置为随机生成;C类数据中的客户地理位置具有显著的集聚特征;RC类数据的客户地理位置同时具有随机分布和集聚分布两种特征.各类客户位置分布如图3所示.
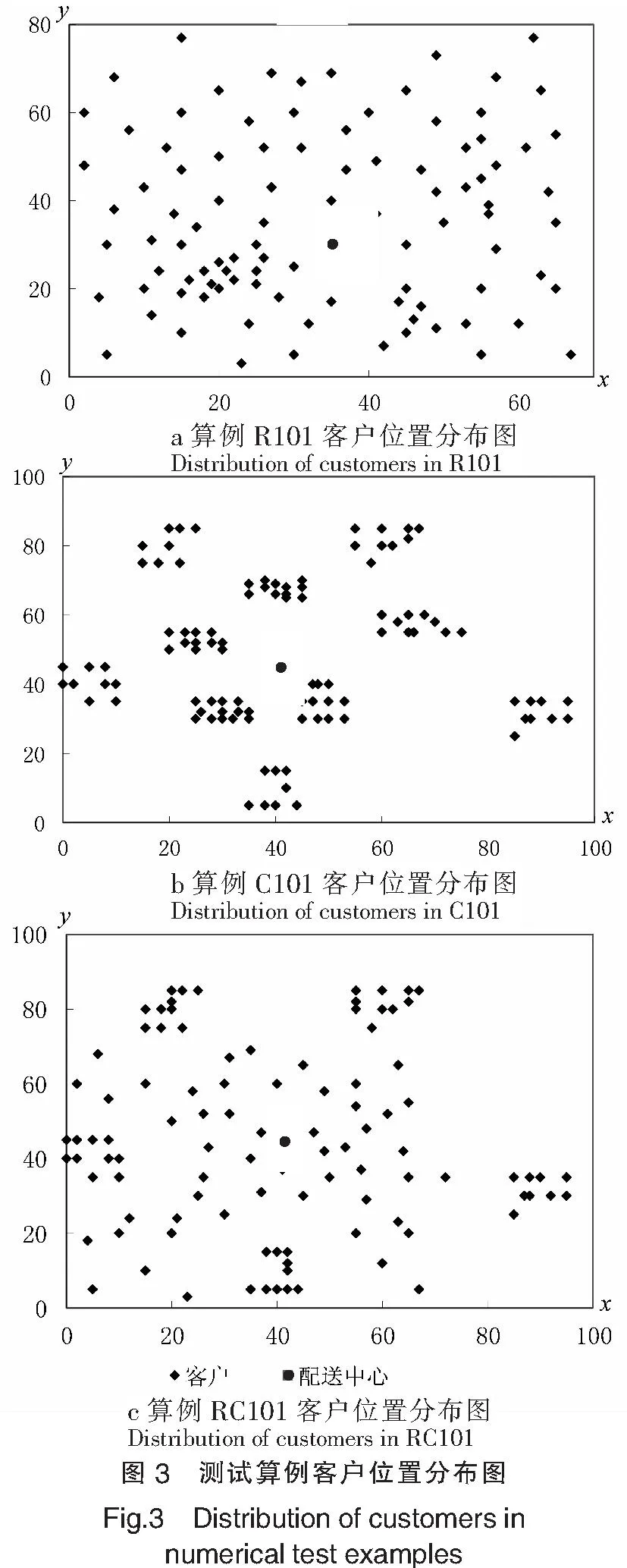
在将动态信息静态化的过程中,定时间隔是一个关键因素.若定时间隔短,则每次优化时客户数较少,能取得较好的优化结果,但同时由于两次优化间隔短,两次优化的客户信息及关键点信息变化不大,也可能造成计算时间和计算资源的浪费;若定时间隔长,则路径优化时无法对客户信息的变化做出最及时的反应,同样无法做出最佳的服务决策.因此,对于测试数据中的100个客户点,分别设置24、48、60、120、40的定时间隔.定时间隔为24时,静态客户数为10,每个定时间隔内出现10个客户;定时间隔为48时,静态客户数为20,每个定时间隔内出现20个客户;定时间隔为60时,静态客户数为25,每个定时间隔内出现25个客户;定时间隔为120时,静态客户数为50,每个定时间隔内出现50个客户;定时间隔为240时,每个定时间隔出现100个客户,即静态问题.实验采用C++语言编程,在Inter Core(TM)i7-3610QM CPU2.3GHz,windows7的主机上运行.
不同定时间隔的求解结果不同,如表1所示.首先,在R101中,最好情况与最坏情况解的差距为8.68%;在C101中,最好情况与最坏情况解的差距为3.37%;在RC101中,该值为15.50%.表明:1)客户的不同地理位置分布对定时间隔的敏感性不同,混合分布最为敏感,其次是随机分布,集聚分布最不敏感.2)总行驶距离长短也并不严格与定时间隔的大小成反比关系,如在R101中,定时间隔24就取得了比定时间隔48要短的总行驶距离,而在C101中,定时间隔24、48、60、120所取得的总行驶距离几乎一致,差异量小于0.43%,在RC101中,也因问题规模越小优化效果越好的原因,定时间隔120反而取得了比定时间隔240(全部静态)要短的总行驶距离.3)由于车辆发出后,只有在剩余容量不足时才返回配送中心,故车辆数在不同的定时间隔设置下并无差异.因此,若客户地理位置为集聚分布时,定时间隔可以设置的稍微大些,能在节约优化计算时间和资源的同时几乎不影响车辆的总行驶路径;而当客户地理位置为随机分布,尤其是当其为混合分布时,则需要慎重制定合适的定时间隔.

表1 不同定时间隔的仿真结果
图4给出了不同客户地理位置分布下不同定时间隔设置时累计客户服务数量曲线,每一时间间隔取最小的定时间隔24作为单位.累计客户服务数曲线表达在不同时刻已经被服务的客户数量,可以作为衡量服务质量的指标之一.在某一时刻,累计服务客户数越多,说明在这一时刻已经被服务的客户数量越多.总的来说,在同一时刻,定时间隔越小的累计客户服务数越大,这是因为定时间隔设置的越小时,初始服务路线越早制定,服务车辆也就越早出发.但是如图4所示,不同定时间隔的累计客户服务数量曲线出现了交叠的现象.在R101中,定时间隔48和定时间隔60的累计服务客户数不相上下,在第16个时间间隔后,定时间隔60的累计服务客户数就超过了定时间隔48的累计服务客户数.结合总行驶距离来看,显然在R101中,定时间隔设置为60优于48.在C101中,定时间隔24、48、60的累计服务客户数都比较接近,和总行驶距离指标显示的结果类似,客户地理位置集聚分布时,对定时间隔的设置不敏感.不过在R101和C101中,定时间隔24的累计客户服务数一直保持在其他定时间隔之上,呈现出一定的优越性.而在RC101中,除定时间隔240(全部静态)外,其余4条曲线均十分接近,定时间隔24、48和60的曲线出现了互相交叠的情况,在第12个时间间隔后,定时间隔48的累计服务客户数就超越了定时间隔24的累计服务客户数,并且定时间隔60的累计服务客户数也与定时间隔24的十分接近,因此当客户地理位置为混合分布时,由于总行驶距离上的优势定时间隔48和60要优于定时间隔24.

6结束语
本文研究了一类动态车辆路径问题,首先,通过定时间隔策略将动态车辆路径问题转化为一系列相应的静态车辆路径问题,分别建立该问题初始优化阶段和实时动态优化阶段的数学模型;其次,设计了模型求解禁忌搜索算法,为了加快寻优速度,利用节约算法为禁忌搜索算法确定初始解,并通过对节约算法中关键点的限制以及禁忌搜索算法中解码过程的设置,使设计的禁忌搜索算法能适用于实时优化阶段的求解;最后,通过对模型的求解,分析了不同客户地理位置分布、不同定时间隔设置下的车辆总行驶距离和累计服务客户数量曲线,实验结果表明,在客户地理位置不同分布时,设置不同的定时间隔对车辆总行驶距离的影响不同,影响最小的是集聚分布,其次是随机分布,对混合分布的影响最大;结合累计服务客户数量曲线,得出了算例R101取定时间隔60较优,算例C101取定时间隔24较优,算例RC101取定时间隔48较优的结论.
[参考文献]
[1]DANTZING G B,RAMSER J H.The truck dispatching problem[J].Management Science,1959,6(1):80-91.
[2]郎茂祥.配送车辆优化调度模型与算法[M].北京:电子工业出版社,2009.
[3]GENDREAU M,GUERTIN F,POTVIN J Y,et al.Parallel tabu search for real-time vehicle routing and dispatching[J].Transportation Science,1999,33(4):381-390.
[4]ZHU K Q,ONG K L.A Reactive Method for Real Time Dynamic Vehicle Routing Problem[C].Vancouver:Proceedings of 12th IEEE International Conference on Tools with Artificial Intelligence,2000:176-180.
[5]HAGHANI A,JUNG S.A dynamic vehicle routing problem with time-dependent travel times[J].Computers & Operations Research,2005,32(11):2959-2986.
[6]ZI N,GENDREAU M,POTVIN J Y.A dynamic vehicle routing problem with multiple delivery routes[J].Annals of Operations Research,2012,199(1):103-122.
[7]陈久梅,张旭梅,肖剑,等.随机动态装卸混合问题的分区求解策略[J].管理科学学报,2012,15(1):43-53.
[8]熊浩,符卓,鄢慧丽.动态车辆路径问题的隐分期灵活分批策略[J].同济大学学报:自然科学版,2013,41(5):676-679.
[9]葛显龙,王旭,邓蕾.基于联合配送的开放式动态车辆路径问题及算法研究[J].管理工程学报,2013,27(3):60-68.
[10]王仁民,闭应洲,刘阿宁,等.改进变邻域搜索算法求解动态车辆路径问题[J].计算机工程与应用,2014,50(2):237-241.
[11]PILLAC V,GENDREAU M,GUÉRET C,et al.A review of dynamic vehicle routing problems[J].European Journal of Operational Research,2013,225(1):1-11.
[12]李兵,郑四发,曹剑东,等.求解客户需求动态变化的车辆路径规划方法[J].交通运输工程学报,2007,7(1):106-110.
[13]张景玲,赵燕伟,王海燕,等.多车型动态需求车辆路径问题建模及优化[J].计算机集成制造系统,2010,16(3):543-550.
[14]王旭,葛显龙,代应.基于两阶段求解算法的动态车辆调度问题研究[J].控制与决策,2012,27(2):175-181.
(责任编辑陈敏英文审校周云龙)
Research on Dynamic Vehicle Routing Problems Based on Two-stage SolvingCHEN Cheng,QIU Rong-zu
(School of Transportation and Civil Engineering,Fujian Agriculture and Forestry University,Fuzhou 350002,China)
Abstract:The idea of two-stage solving is applied and dynamic information is converted into static information by setting timing intervals.Two mathematic models are set up respectively for the periods of initial optimization and real-time optimization.Saving algorithm is used for initial solutions while Tabu search algorithm is used to obtain solutions for vehicle routing issues after initial optimization.In the period of real-time optimization,solutions are obtained after relevant amendments to both algorithms.Then,simulation experiments are carried out to test and analyze settings of time intervals for clients in different geographical locations,and the results prove the simplicity and viability of the proposed solving method.Different sensibilities are shown with different location distributions: mixed distribution is the most sensible to timing intervals;followed by random distribution and then cluster distribution.Finally,the curves corresponding to accumulative numbers of customers served are presented,which,combined with the total travel distances,are used to optimize the setting of timing intervals under different geographic distributions of customers.
Key words:dynamic vehicle routing problems;two-stage solving;timing interval;tabu search
[中图分类号]F253.4
[文献标志码]A
[文章编号]1007-7405(2015)06-0435-07
[作者简介]陈诚(1982—),女,讲师,博士生,从事物流系统优化与仿真研究.通讯作者:邱荣祖(1961—),男,教授,博士,博士生导师,从事物流工程与管理研究.E-mail:875693642@qq.com.
[基金项目]福建省科技厅重点项目(2014H0010);福建农林大学科技创新(培育)团队资助计划(pytd12006)
[收稿日期]2015-04-18[修回日期]2015-07-06

