一个特殊本原有向图的scrambling指数及广义scrambling指数

张佩, 王卓宇, 高玉斌

(1.中北大学 数学系, 山西 太原 030051;2.东华大学 理学院, 上海 201620)

一个特殊本原有向图的scrambling指数及广义scrambling指数

张佩1, 王卓宇2, 高玉斌1

(1.中北大学 数学系, 山西 太原 030051;2.东华大学 理学院, 上海 201620)

主要研究一个含有6个圈的n阶本原有向图,其中包含1个n-1圈,3个n-2圈和2个n-3圈.结合图论与组合论的相关知识,得出该图的scrambling指数和广义scrambling指数.

本原有向图; scrambling指数; 广义scrambling指数;途径

1 预备知识

定义 1[1]设有向图D,若存在一个正整数l,使得D中的任意两个顶点x,y(可以相同),在D中都存在从x到y的l长途径,则称D是本原有向图,其中最小的正整数l称为D的本原指数,记为exp(D).

引理 1[2]有向图D是本原的充分必要条件是D为强连通,且D的所有圈长的最大公因子为1.

定义 2[2]设D是n阶本原有向图,如果存在正整数k,对D中任意顶点u和v,都存在顶点w∈V(D),使得从u和v到w都有k长途径,则称满足上述条件的最小正整数k为本原有向图D的scrambling指数,记为k(D).

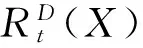
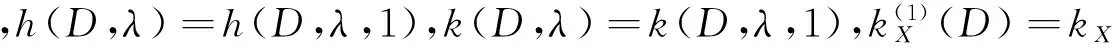
设DT是D的转置,V(DT)=V(D),对于任意的顶点vi,vj∈V(D),弧(vi,vj)∈E(D),当且仅当弧(vj,vi)∈E(DT).根据h(D,λ)的定义,我们有以下三个结论:

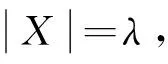
(3)h(D,1)=k(D,1)=1,h(D,n)=k(D,n).

本文主要研究一类含6个圈的本原有向图D(如图1所示)的scrambling指数和广义scrambling指数.

2 主要结果

图1 本原有向图D

定理1 设D是如图1所示的n(n≥7)阶本原有向图,若n≡1(mod2),则有:

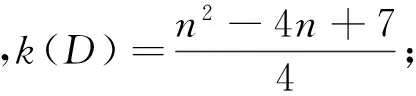
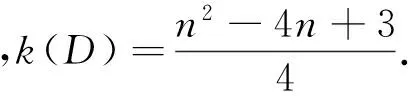
证明 图D中含有1个n-1圈,3个n-2圈和2个n-3圈.

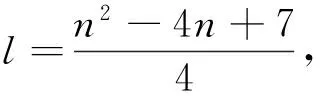
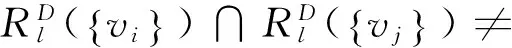
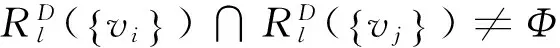
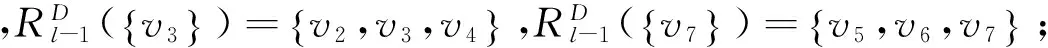
定理 2 设D是如图1所示的n(n≥7)阶本原有向图,若n≡0(mod2),则有:

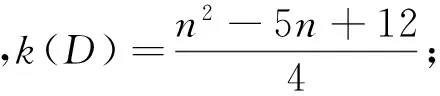
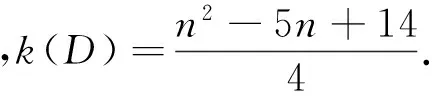
证明 图D中含有1个n-1圈,3个n-2圈和2个n-3圈.

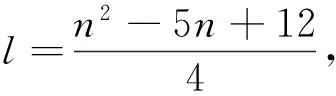
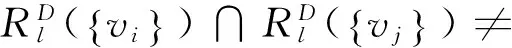
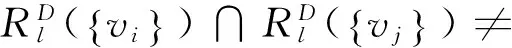
定理3 设D是n阶本原有向图如图1所示,则

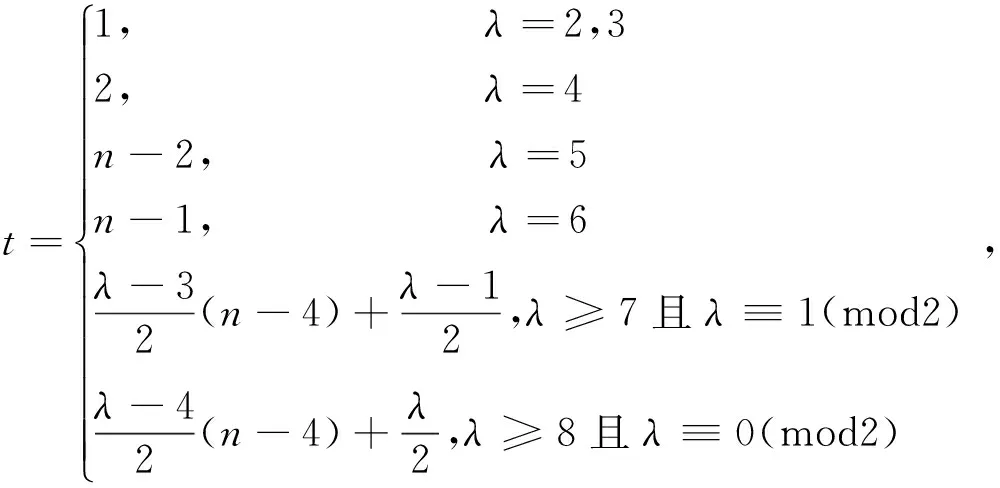
当λ=2,3时,显然h(D,λ)=1.下面证明λ≥4的情况:

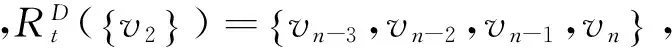
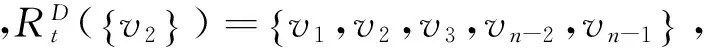
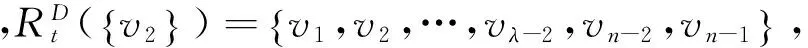
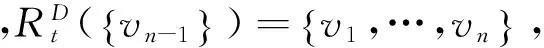
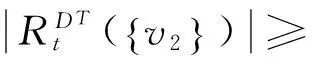
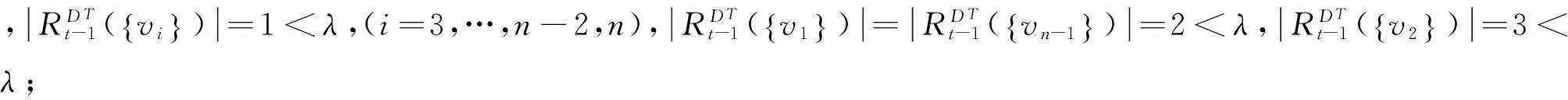
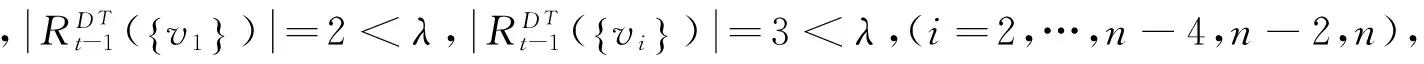
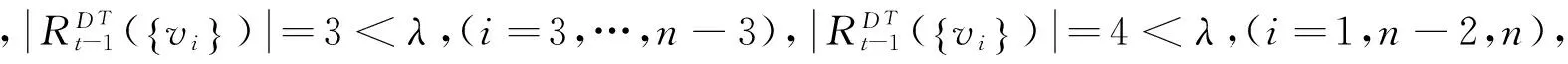
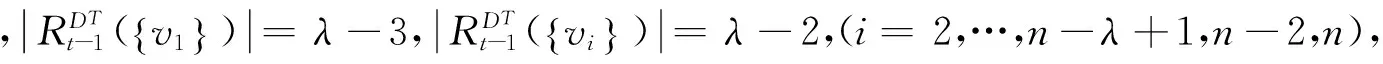
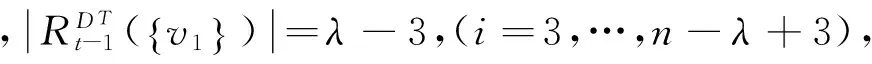
综上所述,h(D,λ)=t.定理得证.

定理 4 设D是n阶本原有向图(如图1)所示,则有

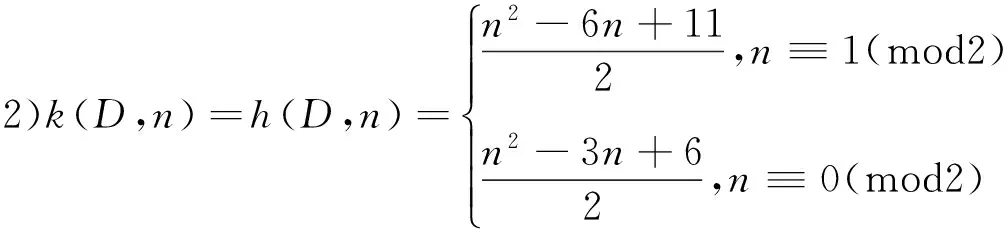
[1] Brualdi R A,Ryse H J. Combinatorial Matrix Theory[M]. Cambridge University Press,1991.

[2] Akelbek M, Kirkland S. Coefficients of ergodicity and scrambling index [J]. Linear Algebra and its Applications,2009, 430:1111-1130.

[3] Liu B, Huang Y. The scrambling index of primitive digraphs [J]. Computers and Mathematics with Applications,2010, 60:706-721.

[4] Huang Y, Liu B. Generalized scrambling indices of a primitive digraphs [J]. Linear Algebra and its Applications,2010, 433:1798-1808.

【责任编辑：王军】

The scrambling index and generalized scrambling indices of a special primitive digraph

ZHANG Pei1，WANG Zhuoyu2,GAO Yubin1

(1.Department of Mathematics, North University of China, Taiyuan 030051, China;2.School of Science, Donghua University, Shanghai 201620, China)

A primitive digraph with five cycles are discussed. It contains one (n-1)-cycle, three (n-2)-cycles and two (n-3)-cycles. Combining with graph theory and combinational theory, the scrambling index and generalized scrambling indices of this primitive digraph are given.

primitive digraph; scrambling index; generalized scrambling indices;walk

2014-09-11

山西省回国留学人员科研资助项目(12-070)

张佩(1989-),女,山西运城市人,中北大学硕士研究生,主要从事图论与组合数学的研究.

O157.5

A

1672-3600(2015)03-0033-04