拓扑模型下的导航地图道路曲率引入

张 攀，郑 珂，王军德，朱敦尧，

拓扑模型下的导航地图道路曲率引入

张 攀1，郑 珂2，王军德2，朱敦尧1，2

( 1．武汉大学卫星导航定位技术研究中心，湖北武汉430079; 2．武汉理工大学智能交通系统研究中心，湖北武汉430063)

一、引言

近年来，道路曲率在汽车导航中的作用逐渐被认识。它在先进驾驶辅助系统( ADAS)中具有广阔的应用前景，如弯道速度提醒、辅助驾驶等［1-2］。弯道速度提醒就是根据弯道的曲率计算出最大行驶速度，提醒驾驶人注意控制车速。然而，目前的导航地图很少包含道路曲率数据，一个重要的原因就是导航数据模型是基于拓扑关系的［3-4］，难以直接引入曲率。如导航地图物理格式Kiwi［5］，道路模型如图1所示。Road A对应一条多线( Multilink)，以点( node)和线( link)为基本存储单元按出现顺序存储。线是两个点的连线段，每个点和线都存储自身的属性值，如点的坐标、线的长度等。这种“直线段”的描述方式可以满足拓扑关系的要求，便于存储和处理，但是不能直接描述道路的曲率特性。因此，国内外研究人员提出了一些道路曲率计算方法与道路曲线描述方法［6-7］，有的甚至在存储上取得了很好的表现［8］。但现有的导航地图数据量大、格式固定，改变道路模型将导致工作量大、稳定性差及导航引擎不支持等问题。因此，如何在不改变道路模型的基础上引入道路曲率数据，是道路曲率走向实际应用的关键。本文的基本思路是:首先在现有导航地图道路数据的基础上计算道路曲率，表现出道路曲率的存在形式;然后探索在拓扑模型下的道路曲率引入方法。

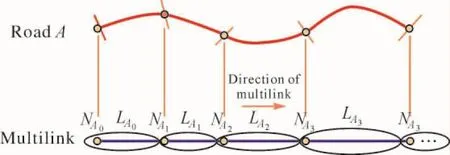
图1 基于拓扑的道路模型

二、道路曲率计算

1．完全曲线拟合

导航地图道路数据中含有节点的坐标数据的完全曲线拟合方法是对道路的离散节点进行曲线拟合。完全曲线拟合采用最小二乘原则，保证拟合误差的平方和最小，得到拟合曲线方程及误差平方和如下

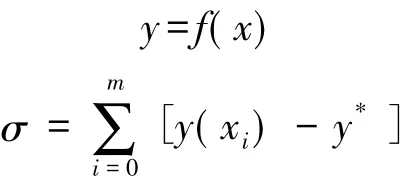
式中，y*为坐标值。

然后求取拟合曲线的曲率。曲率衡量了物体的弯曲程度，是角度微分和弧长微分比值的极限

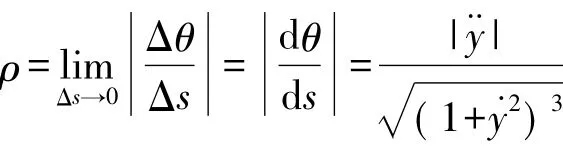
因此，保证拟合曲线二阶可导时，理论上可以计算出拟合曲线上所有点的曲率。在实际应用中为了减少计算量，采取一定的简化。如使用三次B样体曲线拟合道路［9-10］，设当前点坐标为( xi，yi)，上一点坐标为( xi－1，yi－1)，下一个点坐标为( xi+1，yi+1)，则当前点的曲率ρi的计算方法为

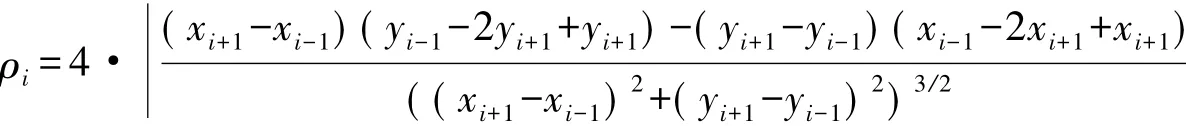
2．组合线形拟合

道路的线路设计主要使用直线、圆曲线、缓和曲线3种线型。一般采用回旋曲线作为缓和曲线，以适应汽车转弯时的行车轨迹，消除曲率突变，增进线性美观及行车舒适感、安全感［11］。组合线型拟合就是使用道路的真实设计线型，即直线、圆曲线和回旋曲线来拟合道路。与完全曲线拟合相比，使用3种固定化的线型拟合，更加接近于道路的真实曲线性质，而且曲率计算更加容易。

首先识别线形，可以理解为将道路按直线、回旋曲线和圆曲线进行分解。简单的方法是根据道路的曲率特征判断，利用方位角的变化判断线型。线路上方位角的变化是曲率沿线路的积分，较曲率而言更容易操作。基本思路是:当方位角的连续变化都接近于0时，识别为直线;当方位角在同一侧保持常值变化时，识别为圆曲线;当方位角在同一侧逐渐递增或递减时，识别为回旋曲线。

然后计算曲率。直线的曲率ρ= 0，圆曲线的曲率ρ=1/R( R为圆半径)。如图2所示，以回旋曲线起点为原点，起点处的切线为X轴，回旋曲线上任意一点P的曲率半径r与该点至曲线起点的曲线长l之积为一常数，即

rl=Q2

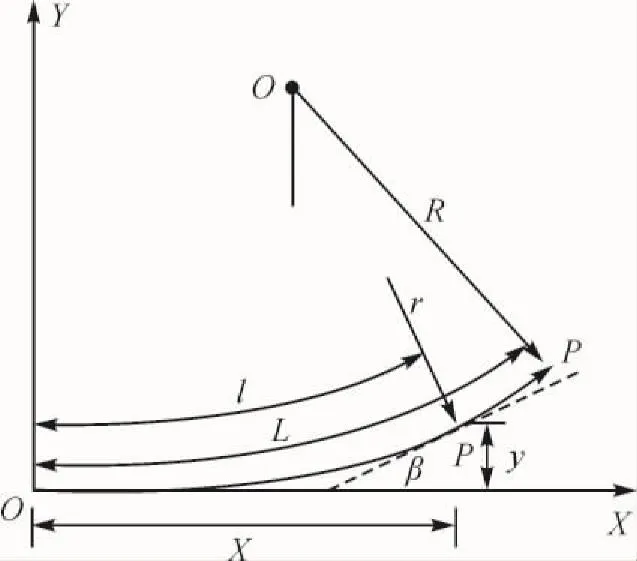
图2 回旋曲线

式中，Q为回旋曲线参数，是表征曲率变化缓急程度的量［12］。根据上式，回旋曲线上任一点的曲率与曲线长成比例，即回旋曲线上距起点l处的曲率为

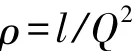
当曲线长等于L时，曲率达到最大值，即

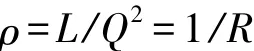
则

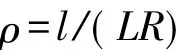
再取P点切线方向角为β角，有

l2=2Q2β

因此

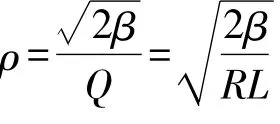
综上，组合线型拟合的道路曲率与道路长的函数图像如图3所示，理论上可以计算出任意点的曲率，同时可以使用常数描述直线和圆曲线部分的曲率。线型参数和曲率具体的计算和讨论，可以参考文献［13］，在此不作详述。

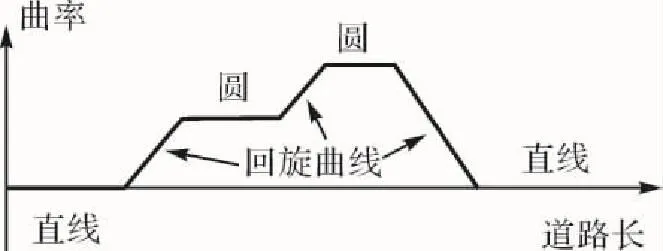
图3 组合线形的曲率特性

三、曲率引入模型

车载导航地图中，对道路数据的逻辑描述常采用3个层次，即数据层、描述层和综合层［14-15］。数据层描述基本图形要素，如点、线、面等;描述层一般用于道路引导和图形显示;综合层存储数据的拓扑结构，主要用于道路计算。曲率作为一种几何特征，可以被引入数据层，不涉及描述层和综合层，使其对导航地图数据模型的影响降到最低。曲率引入数据层，具体而言就是将曲率作为一种几何属性引入点、线和多线，如图4所示。

图4 曲率引入模型

同时，道路曲率的存在形式决定着曲率的引入方式。如通过完全曲线拟合计算曲率，理论上可以计算出拟合曲线上每个点的曲率，但是不能直接表达线的曲率，不便于连续存储和变化趋势分析。组合线形模型可以计算每个点的曲率，同时可以直接表达线的曲率。表1对每种引入方式及其适宜的曲率计算方法进行了介绍，并分析了其优缺点。

表1 曲率引入模型

1．引入点

使用完全曲线拟合计算出的曲率非常适合引入点。直接将点的坐标带入拟合曲线的曲率公式，计算出对应的曲率，然后将曲率作为点的属性即可。需要使用曲率时，直接从点的属性获取曲率。对于使用组合线型计算出的曲率形式(见表2)，点在直线和圆曲线上的曲率值为常值，点在缓和曲线上时带入点坐标求出该点的曲率。

表2 组合线形曲率引入点

2．引入线

使用完全曲线拟合计算出的曲率不适合引入线。使用组合线型拟合，对于直线和圆曲线部分，直接使用常值描述;对于缓和曲线，可以使用平均曲率或曲率变化区间描述，见表3。

表3 组合线形曲率引入线

3．引入多线

曲率引入多线有两种方式:①多线曲率特征值引入。对于已经生成的多线，不必体现每个点或线的曲率，而是选取多线上的曲率特征值作为属性，见表4。如根据某条路的曲率最大值推算最大行驶车速，根据道路上的曲率极值反演道路弯曲情况等，此时，使用完全曲线拟合与组合线型拟合都可以实现依附于多线的曲率引入。②顾及曲率分布的多线生成。多线的生成首先按照道路群分组，道路群是相关道路种别合并后的大类，如国际高速、国内高速等属于高速;然后在每个道路群里面按照道路种别排序，根据拓扑关系和一定的规则探索生成多线，一般要求线的属性相同，包括道路名称、线的种类、通行方向、分离带、道路幅员、地域信息等。顾及曲率分布生成多线，就是在探索生成多线时，顾及曲率的一致性，最理想的情况是直线部分、回旋曲线部分和圆曲线部分，各单独生成一个多线。

表4 多线曲率特征值引入

四、试验与结果

1．试验数据

试验数据采用基于经纬度和基于正规化坐标的两种导航地图道路数据，在Matlab中显示，如图5、图6所示。正规化坐标是导航地图物理格式使用的坐标体系，由一定范围经纬度转换来的区域内相对坐标，如Kiwi格式中Level1的经纬度范围1/32(°)×1/ 32(°)对应到2047×2047的格网区域。

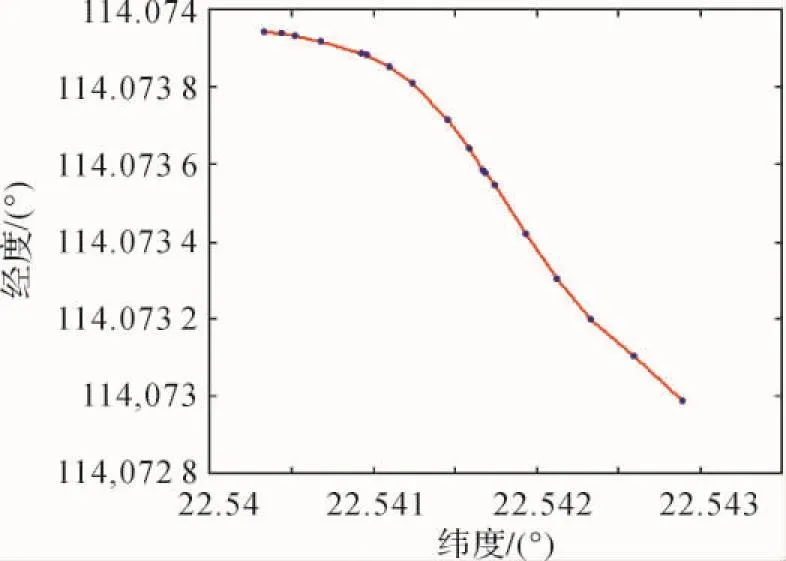
图5 基于经纬度坐标的道路A

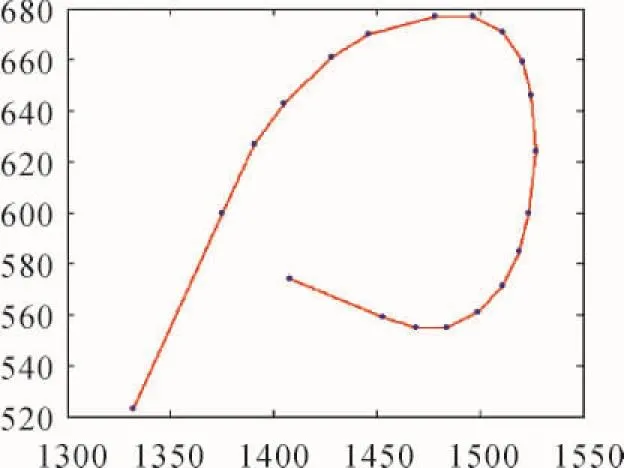
图6 基于正规化坐标的道路B

2．曲率计算试验

使用完全曲线拟合与组合线形拟合两种方法，计算出试验数据的道路曲率，结果如图7所示。由于经纬度单位量表示的地理范围很大，道路节点的经纬度相差很小，因此在计算曲率时，经纬度各乘以105再代入计算。将两组完全拟合与组合线形拟合得到的曲率进行对比，表明组合线形具有较高精确度，可以满足实际需求。

3．曲率引入试验

将引入曲率的道路数据输出可视化工具，发现具有较好的适应性。在不影响拓扑模型使用的同时，可以非常容易获取点、线或多线的曲率属性，如图8所示。

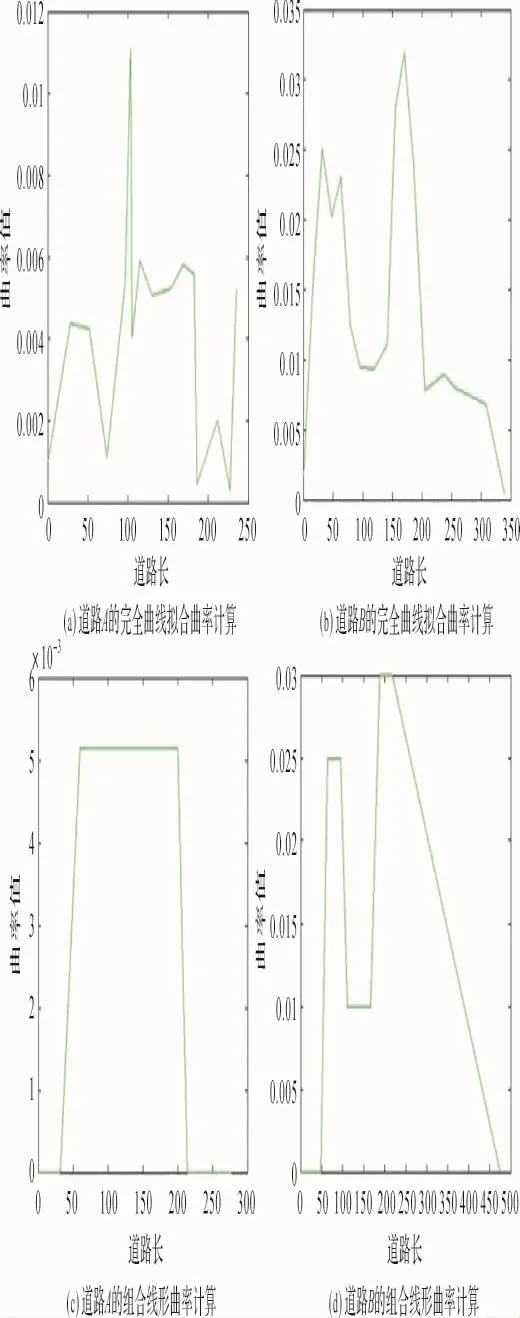
图7 曲率计算试验

图8 曲率引入试验

五、结束语

曲率作为道路的一个真实属性，在传统导航地图中没有得以表达。随着车载导航在汽车主动安全和辅助驾驶方向的发展，道路曲率的重要性被逐渐认识。如何合理引入到现有导航地图的数据模型，是曲率应用的瓶颈问题。本文首先研究了利用导航地图的道路数据计算曲率，提出了完全曲线拟合与组合线形拟合两种方法。然后根据不同的曲率存在方式，探讨了道路曲率的引入方法，分别是引入点、线和多线。引入多线的两种方法中，顾及曲率的多线生成研究尚不完善，其对导航数据的影响程度还需要进一步试验。通过Matlab编程验证了曲率计算两种方法的有效性和精确性，通过可视化试验验证了拓扑模型下道路曲率引入的可行性。今后还需要通过车载导航系统的实车使用，验证引入了曲率数据的导航地图的实用性和稳定性。

［1］ LU M，WEVERS K，HEUDEN R．Technical Feasibility of Advanced Driver Assistance Systems ( ADAS) for Road Traffic Safety［J］．Transportation Planning and Technology，2005，28( 3) : 167-187．

［2］ RESS C，ETEMAD A，HOCHKIRCHEN T，et al．Electronic Horizon-supporting ADAS Applications with Predictive Map Data［C］∥ITS European Congress．Hannover:［s．n．］，2005: 18．

［3］ 张东，钱德沛，王家耀，等．嵌入式环境下导航地图数据表示和并行调度显示算法［J］．武汉大学学报:信息科学版，2007，32( 4) : 343-346．

［4］ 宋莺，李清泉．实时交通信息与移动导航电子地图融合表达［J］．武汉大学学报:信息科学版，2010，35 ( 9) : 1108-1111．

［5］ 徐敬海，李清泉，宋莺，等．基于Kiwi数据格式的地图显示研究［J］．武汉大学学报:信息科学版，2005，30 ( 10) : 866-869．

［6］ 贾立山，罗剑，李世其．基于车道线直线模型的道路曲率估计方法［J］．江苏大学学报:自然科学版，2012，33( 4) : 373-378．

［7］ JIMNEZ F，APARICIO F，ESTRADA G．Measurement Uncertainty Determination and Curve-fitting Algorithms for Development of Accurate Digital Maps for Advanced Driver Assistance Systems［J］．Transportation Research Part C: Emerging Technologies，2009，17( 3) : 225-239．

［8］ BTAILLE D，TOLEDO-MOREO R．Creating Enhanced Maps for Lane-level Vehicle Navigation［J］．IEEE Transactions on Intelligent Transportation Systems，2010，11( 4) : 786-798．

［9］ 李星军，杨海忠．基于曲率分析的地图匹配算法研究［J］．科学技术与工程，2012，25( 29) : 7664-7668．

［10］王献锋．基于曲率分析地图匹配的车载组合导航研究［J］．科学技术与工程，2012，12( 33) : 8947-8950．

［11］叶松林．道路卵形回旋线任意点坐标及方位角计算方法［J］．测绘通报，1999( 3) : 26-28．

［12］徐海贵，王春香，杨明，等．基于曲率平滑的智能车辆道路跟踪控制［J］．上海交通大学学报，2008，42 ( 12) : 1958-1961．

［13］姚连璧．车载GPS道路数据采集与线形参数的计算［J］．测绘学报，2002，31( S1) : 45-49．

［14］ 刘春，姚连璧．车载导航电子地图中道路数据的空间逻辑描述［J］．同济大学学报:自然科学版，2002，30 ( 3) : 346-351．

［15］胥锐．车载导航电子地图的路网模型［J］．电脑知识与技术，2008，3( 7) : 1558-1559．

Introducing Road Curvature into Navigation Map Based on Topological Model

ZHANG Pan，ZHENG Ke，WANG Junde，ZHU Dunyao

随着道路曲率的作用逐渐被认识，道路曲率引入导航地图，成为实现先进驾驶辅助系统( ADAS)的重要途径，也是未来导航地图的发展趋势之一。曲率依附于曲线存在，难以直接引入基于拓扑模型的导航地图。为了避免模型转换带来的巨大工作量和不确定性，本文尝试了拓扑模型下道路曲率引入的研究。首先在现有导航地图道路数据基础上，使用了完全曲线拟合与组合线型拟合两种方法计算曲率;然后结合两种计算方法对应的曲率存在形式，探索了在拓扑模型下的道路曲率引入方式，分别是引入点、引入线和引入多线;最后使用导航地图道路数据进行曲率计算和曲率引入的试验。结果表明，本文的方法具有可行性，为今后大数据量的导航地图道路曲率引入打下了铺垫。

拓扑模型;导航地图;道路曲率;引入

张 攀( 1989—)，男，硕士，研究方向为车载导航电子地图。E-mail: zhangpan@ whu．edu．cn

P282

B

0494-0911( 2015) 11-0052-05

张攀，郑珂，王军德，等．拓扑模型下的导航地图道路曲率引入［J］．测绘通报，2015( 11) : 52-56．

10．13474/j．cnki．11-2246．2015．0345

2014-10-15