“误差理论与测量平差基础”教学系统设计与实现

陶秋香，刘国林，翟 敏

“误差理论与测量平差基础”教学系统设计与实现

陶秋香，刘国林，翟 敏

(山东科技大学测绘科学与工程学院，山东青岛266590)

一、引言

“误差理论与测量平差基础”是测绘类专业的基础核心课程之一，该课程教学质量的高低，教学效果的好坏，会影响学生学习本课程的成绩、后续专业课程的学习质量以及学生毕业后从事测绘生产和科研工作的能力［1-2］。由于本课程教学内容涉及高等数学、线性代数、数字测图、测量学等多个学科，教学中基本概念、数学公式推导多，计算复杂，给教学带来很大的困难。一直是教师难教、学生难学的课程［3-5］。

为了提高“误差理论与测量平差基础”的教学效果，邱卫宁等对该课程的教与学进行了不断的探索和创新，取得了不少的研究成果［6-9］。本文结合目前笔者所在学校本课程建设和教学的实际情况，提出构建“误差理论与测量平差基础”的教学系统，辅助本课程的本科教学，形象地将平差理论与测绘实践结合在一起，从而提高学生学习本课程的积极性和应用测量平差理论解决测绘实际问题的能力。

二、“误差理论与测量平差基础”教学系统设计与开发的必要性

随着GPS、GIS和RS等新技术的不断出现及广泛应用，观测数据和估计量的类型更加多样，测量平差数据处理的要求和任务都在不断提高，“误差理论与测量平差基础”教学中例题和习题的选择也需要更紧密地与测绘实践结合［10］。但由于学时数的限制，并且考虑学生接受的难易程度，教材中所列举的算例、课外的习题、作业，大都是网形简单的水准网和导线网平差。在测量技术日益多样化的今天，这与测绘生产实践是脱节的;课程本身所涉及的理论比较抽象、枯燥，学生对讲授的知识点缺乏感性认识，理解和接受起来比较困难。这些都大大挫伤了学生学习的积极性，致使学生考试成绩分布不合理，与期望值差别较大。

在开设“误差理论与测量平差基础”之前，学生已经具有一定的计算机编程能力，但大多数学生仍很难利用所学编程语言，如C、C++、Matlab等编制测量平差程序，这主要是因为该课程的教学与流行软件和编程语言相结合的切入点太少，影响了学生将所学各课程相通知识融会贯通能力的培养与提高，阻碍了学生创造性思维的培养。

“误差理论与测量平差基础”教学系统的构建就是针对上述教学中的不足，理论联系实际，将课堂上无法完成的复杂但与测绘前沿及实践结合比较紧密的平差实例引入系统，拓宽教学内容和学生视野;同时，让学生利用所学的计算机理论知识和编程语言，编制简单的测量平差程序，加强实践教学环节，提高学生的实践能力，最大限度地发挥主观能动性，改善教学效果。

三、教学系统功能模块与界面设计

“误差理论与测量平差基础”的本科教学紧紧围绕4种基本平差方法，即条件平差、附有参数的条件平差、间接平差和附有限制条件的间接平差进行的。以中国矿业大学张书毕主编的《测量平差》［11］为例，第一章主要讲授用于4种基本平差方法精度评定的协方差和协因数两大误差传播定律;第二章主要讲授4种基本平差方法的数学模型列立及其线性化方法、用于模型解算的最小二乘原理;第三章和第四章主要讲授4种平差方法原理式的推导、应用及其精度评定;第五章主要讲授4种平差方法在测绘工程中的应用实例;第六章主要讲授用于平面控制网精度评定的误差椭圆相关知识。教学中的难点内容较多，如平面控制网条件方程、误差方程的列立、误差椭圆三要素的求解及其绘制等。考虑教学的主要内容、重点、难点和学生学习的薄弱环节。设计了如图1、图2所示的“误差理论与测量平差基础”教学系统的功能模块和界面。

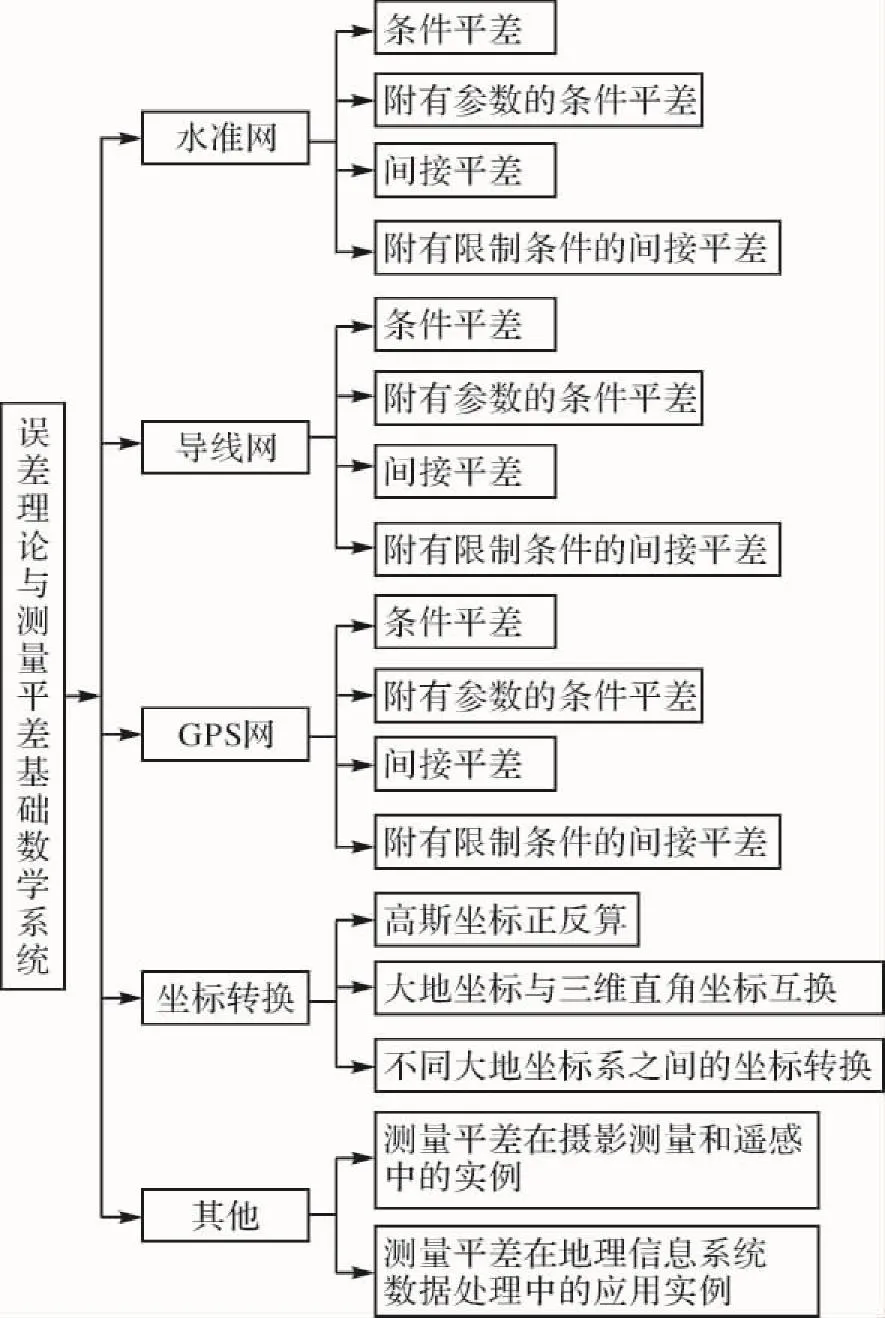
图1 “误差理论与测量平差基础”教学系统功能模块

从图1可以看出，①该系统将测绘工作中常见的水准网、导线网和GPS网的平差问题同时采用4种基本平差方法进行处理，不仅有利于学生更好地掌握各种平差方法的原理、数据处理的流程，还能够使他们充分认识“同一平差问题，在同一最小二乘准则下，无论选择什么平差方法，平差结果所得到的估计量平差值及其方差阵都是相同的”的平差本质，是严密的数据处理方法;②该系统包含了高斯坐标正反算、大地坐标与三维直角坐标互换等坐标转换功能模块。学生在测绘工作中经常会碰到不同坐标系统相互转换的问题，通过该模块的使用和程序编制，学生基本能掌握常用的坐标转换模型和间接平差法在坐标转换中的应用，提高他们分析问题、解决实际问题的实践能力。

图2是在Matlab环境下开发的教学系统界面。该界面采用菜单操作模式，简明扼要，便于学生理解和使用。

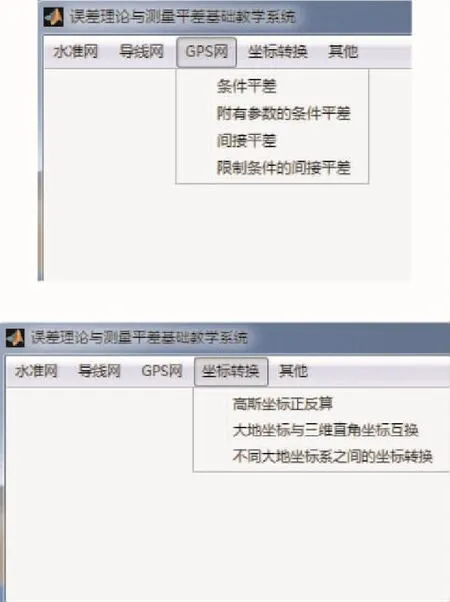
图2 “误差理论与测量平差基础”教学系统界面

四、教学系统的实现与应用

利用C++、VB、Matlab等编程语言均可实现该教学系统。本文结合GPS网间接平差实例，阐述在Matlab环境下该系统的实现方法和流程。

1．界面设计与实现

利用Matlab软件自带的图形用户界面GUI，设计如图2所示的教学系统界面，添加水准网、导线网、GPS网等菜单项及其下拉菜单，即可实现整个系统界面。

2．程序实现

界面布局设计与实现后，即可在界面框架下实现菜单选项的回调，即当点击菜单的某个选项后有相应的平差程序运行。平差程序的实现主要包括观测数据的组织与读入、观测量与待求量近似值的选取与计算、权阵、函数模型系数阵和常数项的计算、观测量与待求量平差值的求解及其精度评定［12-14］。图3为基于Matlab的GPS网间接平差程序设计流程。

图3 基于Matlab的GPS网间接平差程序设计流程

3．应用实例

GPS网平差是以构成GPS向量的三维坐标差作为观测值进行平差，数据处理量大，很难将其作为例题或习题引入课堂教学中。例如，如图4所示是一个相对简单的GPS控制网，其中只有一个已知点和7待定点，测得基线向量16条，各基线向量相互独立(已知点信息、16条基线向量观测值及其对应的方差阵略)。若用间接平差对该网进行平差，需要列出48个误差方程，组成21个法方程解算观测量和待求量的平差值并进行相应的精度评定，手工计算量太大，难以实现。对于这样的习题，学生就可以借助“误差理论与测量平差基础”教学系统，编程实现从数据的组织与输入、误差方程系数阵、观测值权阵的确定直到误差椭圆的绘制的完整平差过程，得出平差结果。图5和图6分别是利用该系统得出的平差结果及其误差椭圆图。

图4 GPS网平差示例

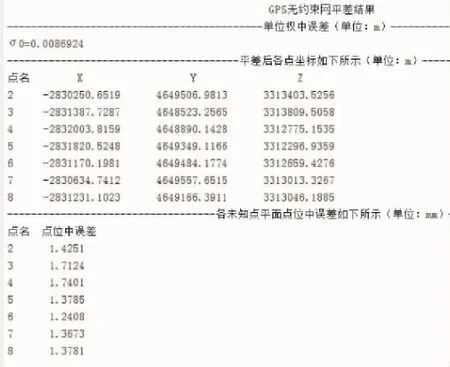
图5 GPS平差结果

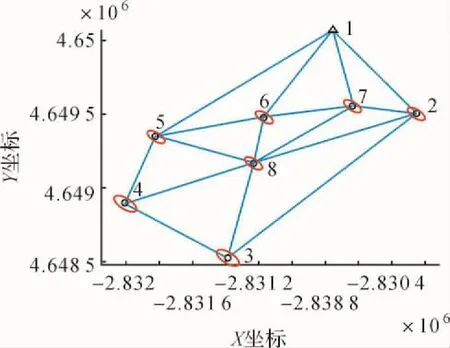
图6 GPS控制网图及其误差椭圆

五、结束语

本文从拓宽教学内容和学生视野、加强实践教学环节、提高学生对理论知识的感性认识等方面，阐述了“误差理论与测量平差基础”教学系统构建的必要性;考虑本课程本科教学的主要内容、重点、难点和学生学习的薄弱环节，设计了“误差理论与测量平差基础”教学系统的功能模块和界面;结合GPS网间接平差实例，给出在Matlab环境下该系统的实现方法、流程及其应用情况。

本文研究结果表明:①“误差理论与测量平差基础”教学系统的开发和使用，能直观地将测绘实践与测量平差数据处理理论相结合，使抽象的理论知识具体化，便于学生理解和接受，提高学习的积极性，进而提高学习成绩;②该系统可让学生利用自己所学的计算机编程语言，结合测绘工作中常用控制网形或其他与测绘前沿及实践结合比较紧密的平差实例，编制简单的平差程序，充分发挥学生自主学习的主观能动性，提高实践能力，更好地为今后的工作或科研打下基础。

［1］ 武汉大学测绘学院测量平差学科组．误差理论与测量平差基础［M］．武汉:武汉大学出版社，2003．

［2］ 张书毕．加强“误差理论与测量平差基础”课程教学的探讨［J］．测绘通报，2004( 5) : 56-57．

［3］ 龚涛．测量平差课程教学探讨［J］．测绘通报，2003 ( 4) : 66-68．

［4］ 黑志坚，周秋生．测量平差教学改革与实践［J］．测绘工程，2001，10( 2) : 59-62．

［5］ 赵宝峰．《误差理论与测量平差基础》课程教学研究与实践［J］．矿山测量，2006( 4) : 73-75．

［6］ 邱卫宁，王新洲，陶本藻．测量平差教学体系的设计与研究［J］．测绘通报，2006( 2) : 67-69．

［7］ 邱卫宁，陶本藻，姚宜斌．误差理论与测量平差基础精品课程的建设与实践［J］．测绘工程，2011，20 ( 1) : 77-80．

［8］ 潘雄．“测量平差基础”课教学探讨［J］．中国地质教育，2006( 4) : 121-123．

［9］ 蔡群，赵宝峰，崔旭升．《测量平差基础》教学改革探索［J］．中国成人教育，2005( 1) : 79-80．

［10］姚吉利，孔维华．测量平差基础例题和习题选择方案［J］．测绘通报，2004( 7) : 57-59．

［11］张书毕．测量平差［M］．徐州:中国矿业大学出版社，2008．

［12］董春来．MATLAB语言及测绘数据处理应用［M］．成都:西南交通大学出版社，2012．

［13］李建章，陈海鹰，纪凤仙，等．测量数据处理程序设计［M］．北京:国防工业出版社，2012．

［14］张红华．Matlab软件对测量平差教学的启示［J］．矿山测量，2013( 2) : 96-99．

Design and Implementation of Error Theory and Surveying Adjustment Basis Teaching System

TAO Qiuxiang，LIU Guolin，ZHAI Min

为扩充教学内容、改善教学效果、辅助本课程的本科教学，提出了构建“误差理论与测量平差基础”的教学系统。结合目前笔者所在学校本课程本科教学的实际情况，论述了构建“误差理论与测量平差基础”教学系统的必要性;基于教学的主要内容、重点和难点，设计了教学系统的功能模块和系统界面;以Matlab环境下GPS网间接平差为例，阐述了该系统的实现方法、流程和应用。研究结果表明，该系统可加深学生对课堂理论知识的感性认识，充分发挥学生自主学习的主观能动性，提高实践能力。

误差理论与测量平差基础;教学系统; Matlab; GPS网间接平差

陶秋香( 1977—)，女，博士，副教授，主要研究方向为InSAR监测地表形变的原理与应用等。E-mail: qiuxiangtao@ 163．com

book=128,ebook=131

G64

B

0494-0911( 2015) 11-0125-04

陶秋香，刘国林，翟敏．“误差理论与测量平差基础”教学系统设计与实现［J］．测绘通报，2015( 11) : 125-128．

10．13474/j．cnki．11-2246．2015．0363

2014-07-10

山东科技大学教学研究项目( qx2013210)