激光干涉测量三维点坐标的PDOP模型研究和应用

范百兴，李广云，李佩臻，易旺民，杨 振

激光干涉测量三维点坐标的PDOP模型研究和应用

范百兴1，李广云1，李佩臻2，易旺民3，杨 振1

( 1．信息工程大学，河南郑州450001; 2．河南省基础地理信息中心，河南郑州450003; 3．北京卫星环境工程研究所，北京100094)

一、引言

激光跟踪仪采用激光干涉测距IFM( Interferometer)原理，测距误差小于0．5 μm/m，但其测角误差可达到( 15 μm+6 μm/m)，是影响激光跟踪仪点位误差的主要因素。可采用激光干涉的精密距离观测值建立高精度的三维控制网，通过N( N≥3)台激光跟踪仪的距离交会精密测量空间点的三维坐标值，消除角度误差影响，提高点位测量精度。

基于激光跟踪仪的激光干涉测距三维网由于没有角度观测值，其对控制网的横向误差控制较差，空间点位误差受测站点和测量点之间的空间位置关系影响较大。三维位置几何精度衰减因子( position dilution of precision，PDOP)从本质上讲就是误差放大因子，即在空间点的三维坐标解算中，激光跟踪仪的测距误差被放大PDOP倍得到位置误差。也就是说，在激光跟踪仪测距激光干涉测距精度一定的条件下，空间点的三维坐标测量精度随着空间位置的不同而不同。本文在加权秩亏平差模型的基础上，建立了激光干涉测距三维网的PDOP值计算模型，实现了点位精度的先验估计，并对实际算例进行了计算，以避开不利方向，提高点位测量精度。

二、激光干涉三维测边网PDOP值解算模型

如图1所示，设i( i=1，2，…，m)台激光跟踪仪对空间点j( j=1，2，…，n)进行了激光干涉距离测量，距离观测值为Sij，其中m≥3。设测站坐标分别为(i，i，i)，j点的坐标值为(j，j，j)，则距离测量方程为

图1 激光干涉交会测量示意图

对式( 1)进行线性化即可得到误差方程为

式中，cij、dij、eij为线性化系数; lij为自由项。在激光干涉三维测边网中，只有长度而无位置和方位信息，属于秩亏自由网平差，必须加入约束矩阵G才能解算［1］。当测站坐标(i，i，i)已知且m≥3时，即为空间距离前方交会，式( 2)可变为

式中，系数cij、dij、eij中的测站坐标值已知。按照最小二乘原理可得

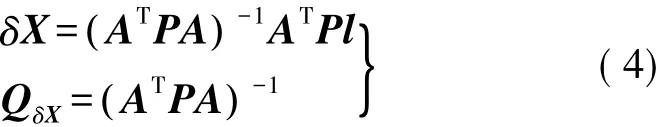
未知参数中误差为

从式( 5)中可以看出，激光干涉三维测距网和距离交会测量时，在单位权中误差一定的情况下，点位精度随着系数矩阵A变化，空间点的三维坐标中误差为

系数矩阵是测站点和测量点空间位置的反映，则空间点三维位置几何精度衰减因子为

三、PDOP值的仿真解算

以L1、L2、L33台激光跟踪仪距离交会测量为例，则误差方程的系数矩阵为

设3台激光跟踪仪测站坐标为L1( 0，0，0)、L2( 0，0，1000)、L3( 0，5000，0)，则XOY平面内，X在－10～+10 m内的PDOP值的分布如图2所示。

图2 XOY面内测量点PDOP等值线分布

图中带数值的线是以5为等间距的PDOP等值线，其余是以1为等间距的PDOP等值线，为了图形的清晰，在PDOP等值线梯度变化剧烈的区域，只显示了以5为等间距的PDOP等值线。

从图2可以看出，在XOY平面内，测量点的PDOP值随着离测站点距离的增加而增加，在接近直线L1L2L3时，PDOP值急剧增加，对应的点位精度也会急剧降低。XOY平面的PDOP等值线分布图形随着Z值的不同会发生变化，但是趋势是一致的。此外，在Y轴负方向上，PDOP等值线分布图和Y轴正方向上对称分布。进一步可以得到YOZ( X = 1)平面和XOZ( Y= 0)平面内的PDOP等值线分布图，分别如图3和图4所示。

图3 YOZ面内测量点PDOP等值线分布

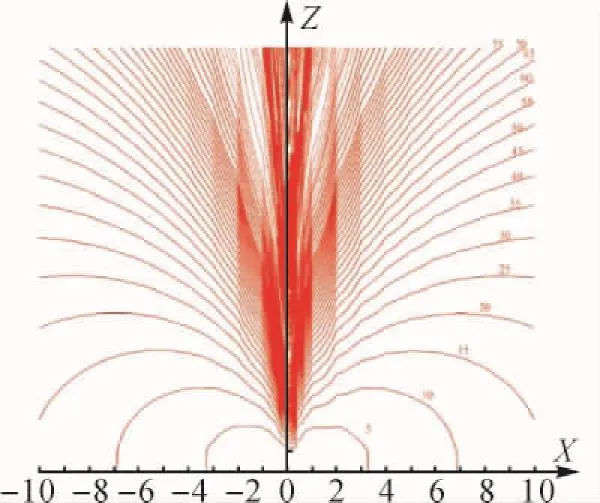
图4 XOZ面内测量点PDOP等值线分布

四、测站数对PDOP的影响

从理论上讲，对空间点进行距离交会测量时，测站数和测站分布都直接影响PDOP值。在3台激光跟踪仪L1、L2、L3的距离交会测量空间点的基础上，增加一台激光跟踪仪L4( 2000、6000、2000)，则此时存在多余观测，可以按照最小二乘原理进行空间点三维坐标求解，在XOY平面( Z=0)处的PDOP等值线图如图5所示。

图5 4台激光跟踪仪交会时XOY面PDOP等值线分布

比较图2和图5可以发现，4台跟踪仪在进行激光干涉交会测量时，其在XOY平面内的PDOP等值线分布明显优于3台交会测量时的情况。此时，整个XOY平面内的PDOP等值线分布变化比较均匀，不存在PDOP值剧烈变化的区域，PDOP值只是随着距离的增加而均匀缓慢地变化。因此，增加激光跟踪仪的数量，可以显著降低PDOP值，提高点位测量的精度。进一步，当新增测站在四面体PL1L2L3的表面或内部时，P点的PDOP值几乎没有变化，若新增测站在四面体外部时，对P点的PDOP值影响明显。

五、体积与PDOP的关系

在图1中，测量点P与3台激光跟踪仪L1、L2、L3的连线可以组成四面体P-L1L2L3，则四面体PL1L2L3的体积V为

进一步，当激光跟踪仪的个数m≥4时，则各个测站和交会点之间的连线可以分解为m－2个四面体，则此时的体积为

分析式( 9)和式( 8)可以发现，体积和PDOP值的计算公式中都包含测量点与测站点的坐标差值因子(Δx01，Δy01，Δz01)。也就是说，体积值和PDOP值都与激光跟踪仪的测站与交会点的空间位置有关，即三维位置几何精度衰减因子即与四面体的体积V相关［2］

随着四面体体积的增大，多台激光跟踪仪交会测量点的精度会得到提高，为提高激光跟踪仪交会测量的点位精度，一般要求PDOP值尽可能小，即所构成的四面体的体积尽可能大。

六、数据解算

为解算PDOP值和点位误差，采用徕卡AT901-B激光跟踪仪在实验室内共布设了L1—L8共8测站，测站间的最大高差约为0．4 m，各个测站近似水平，每测站对13个定向点进行测量，定向点均匀分布且最大高差约为1．5 m，其中P1—P8位于地面上，其他点位于墙壁上。

按照加权秩亏自由网平差模型，同时解算测站点和定向点的PDOP值及其与空间体积，结果见表1和表2。

表1 测站点平差结果

表2 定向点平差结果

从表1和表2可以看出:

1)点位误差和PDOP值之间呈现严格的线性关系。

2)体积值和PDOP值及点位误差之间具有一定的相关性，但是与空间距离交会测量点坐标不同，由于激光干涉测距三维网的空间图形复杂，对PDOP值的影响比较复杂，体积值与PDOP值的相关性不强。

3)由于测站之间的最大高差只有0．4 m，导致定向点的PDOP值较大(平均值为3．6)，体积值较小(平均值为3．8 m)，点位精度较低(平均值为16．5 μm)。

4)定向点分布均匀且最大高差为1．5 m，因此测站点的PDOP值很小(平均值为2．5)，体积值较大(平均值12．6 m)，点位精度较高(平均值11．7 μm)。

根据上述规律，在实际测量中可以加大激光跟踪仪之间的高差，减小PDOP值，以提高点位测量的精度。

七、结论

1)基于激光跟踪仪的激光干涉三维测距网的PDOP解算模型，较好地反映了测站点和定向点的空间分布对点位精度的影响规律，可以获取PDOP值的空间分布等值线图，在测量之前可以对空间点位精度进行估算，根据点位的先验精度估计值，选择最优测量位置，最大限度地提高点位测量精度。

2)体积和PDOP值之间存在相关性，在体积一定的情况下，PDOP值受测站点位空间分布的影响比较明显，二者之间接近似为反比关系。

3)增加测站点之间高差和定向点之间的高差，可以增大测站点和定向点的体积值，对象的PDOP值也会显著提高，从而使对应的点位精度也得到提高。

4)当新增测站在原有四面体之外时，对减小测量点的PDOP值的作用非常明显，可以消除PDOP值剧烈变化区域，但是新增测站在原有四面体表面或内部时，对测量点的PDOP值改变几乎没有影响。

［1］ 黄维彬．近代平差理论及其应用［M］．北京:解放军出版社，1992．

［2］ 许其凤．GPS卫星导航与精密定位［M］．2版．北京:解放军出版社，2001．

［3］ 李广云，李宗春．工业测量系统原理与应用［M］．北京:测绘出版社，2011．

［4］ 杨凡，李广云，王力．激光跟踪仪与球形反射器综合性能测试研究［J］．测绘通报，2014( 2) : 115-118．

［5］ 李国重，李建文，焦文海，等．顾及卫星故障修复的导航星座PDOP可用性分析方法研究［J］．武汉大学学报:信息科学版，2010，35( 7) : 841-845．

［6］ 罗涛，董岚．基于激光跟踪仪三维控制网严密平差与软件实现［J］．北京测绘，2011( 1) : 1-3，7．

［7］ 王丹丹，王小军，陈小军，等．陆基导航三站定位与四站定位PDOP值分析［J］．航天控制，2009，27 ( 5) : 15-19．

［8］ The American Society of Mechanical Engineers．ASME B89．4．19—2006 Performance Evaluation of Laser-Based Spherical Coordinate Measurement Systems［S］．New York: The American Society of Mechanical Engineering，2006．

［9］ YANG S，HUANG G C．Simulation and Analysis of Performance on the Compass Enhanced by GEO and IGSO ［J］．Journal of Electronics ( China)，2011，28( 2) : 235-238．

［10］余航华，何赟晟，周世宏．导航星座的覆盖特性和定位精度因子分析［J］．全球定位系统，2010，35( 6) : 30-34．

［11］杨春燕，吴德伟，余永林，等．干涉式量子定位系统最优星座分布研究［J］．测绘通报，2009( 12) : 1-6．

PDOP Model of Laser Interferometry 3D Trilateration Network

FAN Baixing，LI Guangyun，LI Peizhen，YI Wangmin，YANG Zhen

激光跟踪仪的激光干涉测距精度可以达到0．5 μm/m，利用激光干涉精密距离测量值可以建立高精度的三维控制网，点位误差受到测站点和定向点的空间几何分布影响。建立三维位置几何精度衰减因子模型，可以计算空间点的三维坐标测量精度随着空间位置的变化，估算激光干涉三维测距网的先验精度信息，避免不利测量位置，提高空间点测量精度。本文基于激光干涉三维测距网PDOP值计算模型，仿真计算了PDOP值的空间分布等值线模型，分析了体积值与PDOP值和点位误差的关系，并对实际算例进行了解算。

激光跟踪仪;激光干涉测距;三维测边网; PDOP值;等值线

范百兴( 1978—)，男，副教授，主要从事精密工业与工程测量方面的研究。E-mail: fbxhrhr@ sina．com

P237

B

0494-0911( 2015) 11-0028-04

范百兴，李广云，李佩臻，等．激光干涉测量三维点坐标的PDOP模型研究和应用［J］．测绘通报，2015( 11) : 28-31．

10．13474/j．cnki．11-2246．2015．0339

2014-11-23

国家自然科学基金( 41101446) ;航天器高精度测量联合实验室基金