履带式爬壁机器人受力分析与稳定性仿真研究*

熊 雕，刘玉良

(浙江海洋学院船舶与海洋工程学院，浙江舟山316022)

0 引 言

爬壁机器人可搭载多种工具在垂直墙壁上移动，能够执行高难度任务，在石化、能源、船舶、建筑等行业应用前景广阔［1］。爬壁机器人有滑架式、多足式、轮式、履带式等结构类型［2］，其中履带式应用较为广泛。相对于多足爬壁机器人，履带爬壁机器人的优点在于移动速度更快，但缺点是路面适应性较差。履带机器人与轮式机器人相比，速度虽慢，但可以越过更大的障碍物。总之，履带机器人的主要优势是稳定性好、适应能力强，可以搭载更多传感器执行更为复杂的任务，因而得到了广泛应用。

关于爬壁机器人的应用研究，国外已有46年的历史，特别是日本欧美等国的著名院所，在履带爬壁机器人基础理论和试验方面做了大量研究工作。国内方面，衣正尧等人［3］研制了船舶上用于除锈的爬壁机器人，并进行了动力学建模与分析，主要研究了影响电机转矩的因素，但理论研究结果与相关文献的实验结果相差较大，无法为爬壁机器人的优化提供理论依据。文献［4］论述了爬壁机器人的动力学建模、仿真和实验，但没有对磁铁吸附力与运动性能的关系做理论分析。目前已报道的大量文献中，很多仅进行履带爬壁机器人建模和仿真验证，分析和优化方面的文献较少。

本研究针对履带试爬壁机器人的结构特点，分析爬壁机器人壁面运动的受力情况，对载荷分布系数的概念进行修正，然后建立完整的运动模型，并对永磁铁的吸附力、电机所需转矩、壁面倾角和载荷分布系数之间的关系，进行全面分析和仿真，确定载荷分布系数和壁面倾角对所需的电机转矩和永磁铁吸附力的影响。

1 壁面静力学分析

下面本研究以大型油罐容器检测为应用背景，分析永磁吸附履带式爬壁机器人的受力情况如图1所示。

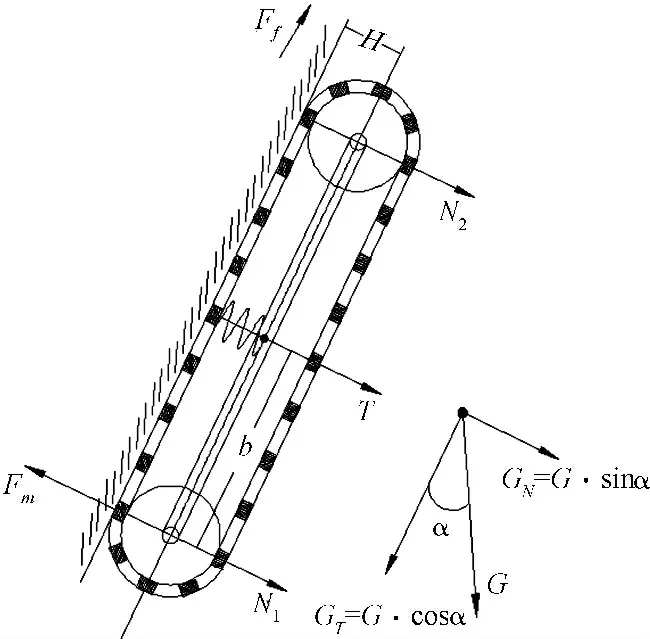
图1 爬壁机器人壁面受力图

爬壁机器人的履带是通过铰链联接，在垂直于牵引力的方向上没有刚性，所以不能将垂直于履带平面的载荷分布到每个永磁体上，这是爬壁机器人工作稳定性不高的主要原因［5］。本研究假设机器人上有分布载荷，并把载荷分散机构等效为一个弹簧，将机器人在GN方向上受到的力，分散到吸附在壁面的其他磁铁上，且单条履带上载荷分散机构产生的总拉力为弹簧的弹力T。有文献定义载荷分散系数uL= 1－ΔWmax/W，其中:ΔWmax—吸附面上各永磁铁所承受载荷的最大差值，W—总载荷。很明显ΔWmax难以测量或计算，导致uL难以计算，而T 相对于ΔWmax更便于测量或计算，因此为了便于分析uL对爬壁机器人稳定性的影响，本研究将载荷分散系数重新定义为uL=2T/G。

下面研究载荷分散系数对机器人爬壁稳定性的影响。由于弹簧的变形量在机器人运动过程中保持不变，可认为由载荷分散机构产生的拉力始终为T。为保证爬壁机器人不会从壁面掉下，作用在其上的外力应满足静力学平衡方程组。

其中，文献［6］中的方程组为:

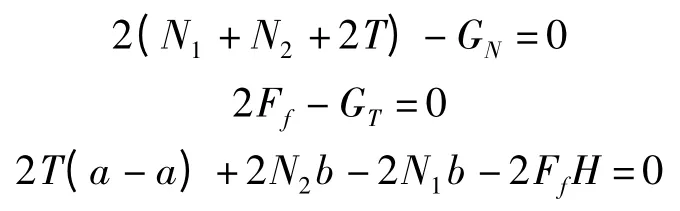
式中:Ff—单条履带受到的摩擦力，其大小与1/2GT相等，个人认为这种定义对分析计算无任何帮助。这里笔者将Ff定义为最大静摩擦力，只要满足Ff≥GT，机器人就不会沿壁面下滑，可依据此条件计算磁铁所需要的吸附力，并额外引入了载荷分布系数uL的概念，将uL替换T，分析uL对N1、N2影响，为吸附力优化提供依据。

改进后方程组为:

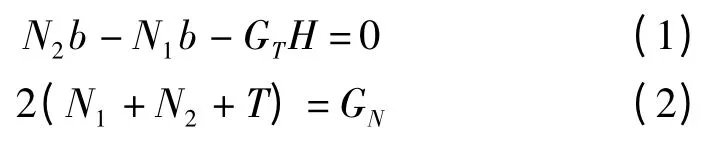
由式(1，2)得到:

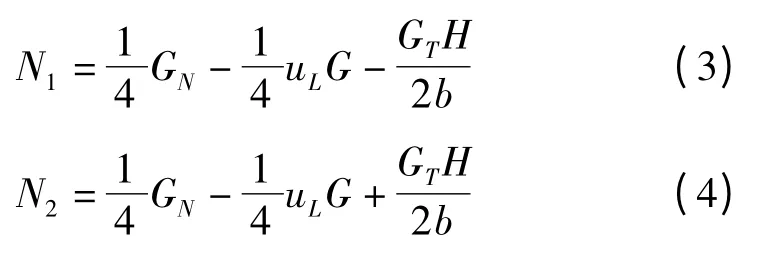
式中:N1，N2—机器人在垂直于履带方向上对吸附在墙壁上的最下面和最上面的电磁铁的拉力;Ff—两条履带与壁面间的最大静摩擦力;G—整个机器人的重力，GT=Gcosα，GN=Gsinα;b—支撑力N1、N2相对与机器人重心的力臂;H—摩擦力Ff相对于机器人重心的力臂。

要保证机器人在壁面上不向下滑动，须有:

Ff≥GT

其中:

Ff=(nFn－GN)u，

式中:Fn—单个磁铁的吸附力，n—永磁铁的个数，u—摩擦系数。

将Ff=(nFn－GN)u 代入到Ff≥GT可得到单个电磁铁所需的吸附力:

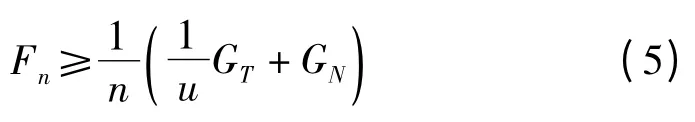
机器人上爬过程要保证机器人在壁面上不发生翻转，必须使最上面一块磁铁不被掀起，即:

Fn≥N2

将式(4)代入上式有:

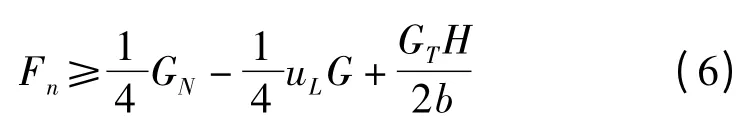
2 机器人沿壁面运动的受力分析

2．1 沿壁面匀速运动的受力分析

机器人如果上爬，单边履带上的电机驱动转矩应克服1/2 重力转矩和Mf［7-8］。而关于Mf的计算，相关文献有所不同，经综合分析多篇文献，重新计算了Mf，得到下式:

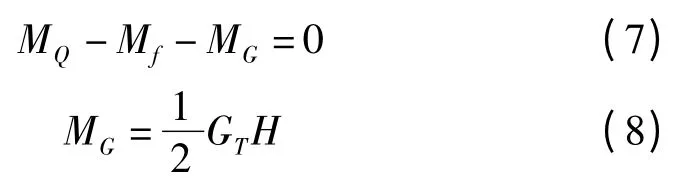
式中:MQ—单侧电机经减速后的输出驱动转矩;Mf—机器人履带上最下面一块电磁铁由于受力产生的阻力矩;MG—1/2 重力产生的转矩;F1—履带最下面一块磁铁对壁面的压力，且F1=Fn－N1。因此有:

将式(8，9)代入式(7)，可得到单侧电机所需驱动转矩:

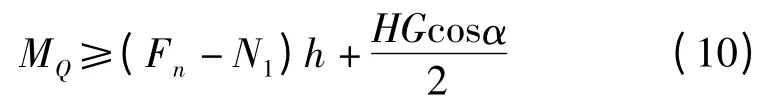
2．2 沿壁面转弯运动的受力分析

文献［9］中对转弯运动模型进行分析时，仅考虑总摩擦阻力矩MZ的影响，而MZ推导过程不明确，与文献［10］推导过程不同，在分析时也未考虑Mf和重力对电机驱动力矩的影响，且对运动模型的仿真结果与相关文献的实验结果不同。其电机力矩方程为:

Mq≥MZ

履带机器人一般通过两条履带的差速实现转弯，而在实际设计时，都是通过正、反转两条履带实现机器人的转弯功能。假设机器人的重力主要分布在两侧履带上，本研究在分析转弯运动模型时，充分考虑了摩擦阻力矩MZ、Mf和GT对电机所需驱动力矩的影响。

机器人在壁面向右转弯时，左侧履带所需力矩大于右侧履带力矩［11-14］，所以机器人转弯时履带所需的力矩方程为:

式中:Mq—履带驱动力矩;MZ—履带上每块磁铁与壁面的摩擦力合力所产生的摩擦阻力矩;(1/4)GTL—机器人左侧质量产生的力矩。其中:

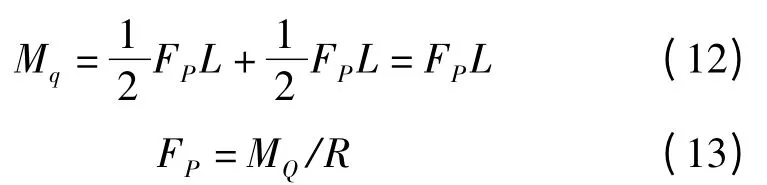
合并式(12，13)得到:

履带机器人在转弯时，接触面压力不均匀分布的程度越显著，摩擦阻力反抗履带转弯的阻力越小，所以压力均匀分布时所受转弯阻力矩最大，这里的压力按均匀分布计算，则有:

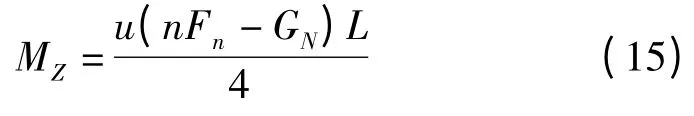
联立式(9，11，14，15)可得到转弯时电机所需的驱动转矩:

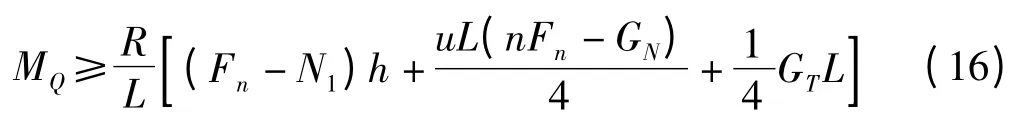
3 实验及结果分析

机器人物理参数设置参照文献［6］，即G =700 N，u=0．5，H=0．112 m，b=0．3 m，L=0．6 m，R=0．08 m，n=30。

3．1 磁铁所需吸附力

首先以机器人在壁面不滑动为约束条件，根据式(5)，通过仿真分析可得单个磁铁所需吸附力与壁面倾角的关系如图2 所示。为保证机器人不滑动，壁面倾角对单个磁铁所需吸附力有很大影响，本研究对式(5)进行求导，发现壁面倾角为26．1°时所需电磁铁吸附力最大，为FN=52．17 N;然后以机器人在壁面不翻转为约束条件，利用式(6)，通过仿真分析可得单个磁铁所需吸附力与壁面倾角和载荷分布系数的关系如图3 所示。壁面倾角和载荷分布系数对单个磁铁所需吸附力都有很大影响，为保证机器人不翻转，单个磁铁所需吸附力随载荷分布系数uL增大而减小，对式(6)求导计算得，机器人在uL=0，α =53．1°时，单个磁铁所需吸附力最大，Fn=218 N。在下面的仿真中，为保证机器人稳定运行，将单个磁铁的吸附力设定为218 N。

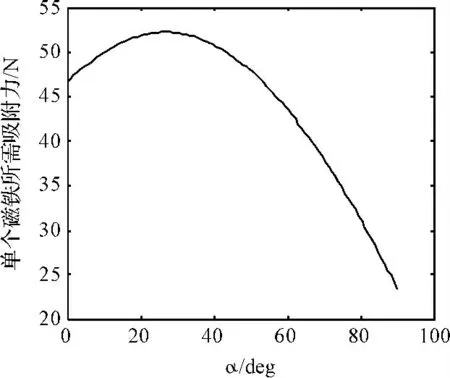
图2 单个磁铁所需吸附力与壁面倾角的关系

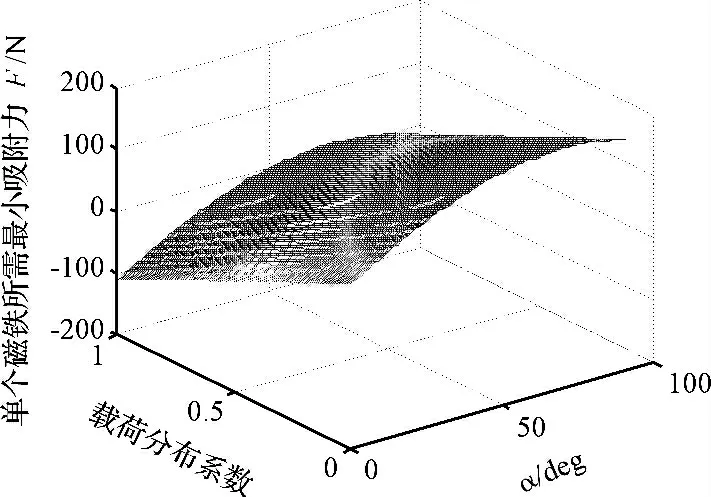
图3 保证机器人不翻转所需的单个磁铁的吸附力

3．2 电机所需转矩

下面设定参数Fn=218 N，其余物理参数不变，根据式(10)，通过仿真分析机器人直线上爬时电机所需转矩与载荷分布系数和壁面倾角的关系如图4 所示。可见，直线运动时电机所需驱动转矩随α 角增大而减小，随uL增大而增大;在同一α 的前提下，不同uL所对应的电机所需最小驱动转矩的变化范围只有5 N·m，因此在磁铁吸附力确定的条件下，直线上爬时电机所需驱动转矩受uL影响很小，其大小主要是由α 决定，其最小所需驱动转矩为48 N·m。

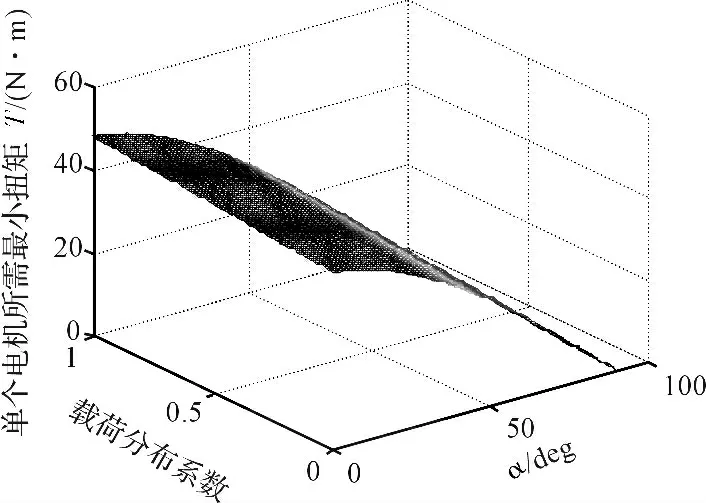
图4 上爬时电机所需转矩与uL 和α 的关系

本研究设定参数Fn=218 N，其余物理参数不变，根据式(16)，通过仿真分析零转弯半径时电机所需转矩与载荷分布系数和壁面倾角的关系如图5 所示。转弯时电机所需最小驱动转矩为72 N·m，大于48 N·m，主要是因为电机还要额外克服转动摩擦阻力矩，其值比直线上爬所需转矩要大，且其转矩也是随α 的增大而减小，随uL的增大而增大，但对于不同uL所对应的电机所需最大驱动转矩最大差值只有1 N·m，因此在磁铁吸附力确定的条件下，转弯时电机所需驱动转矩主要受α 影响，uL对其产生的影响可以忽略。

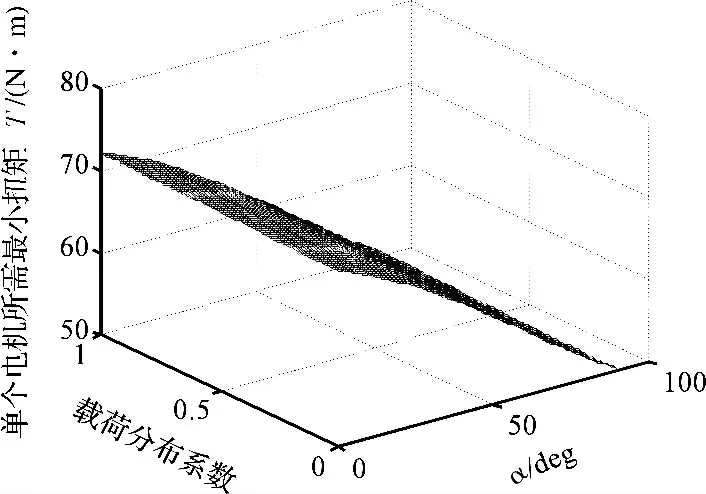
图5 转弯时电机所需转矩与uL 和α 的关系

由于参数过多，图4 和图5 都未分析磁铁吸附力对电机转矩的影响，在此本研究设定参数uL=0．5，α =30°，对式(10，16)进行仿真，分析磁铁吸附力对电机转矩的影响。磁铁吸附力与电机所需驱动转矩的关系如图6 所示。由图6 可以看出，机器人作直线运动时电机所需转矩受磁铁吸附力的影响不大，而转弯运动时电机所需转矩受磁铁吸附力的影响很大，仿真结果与文献［5］的实验结果相同。

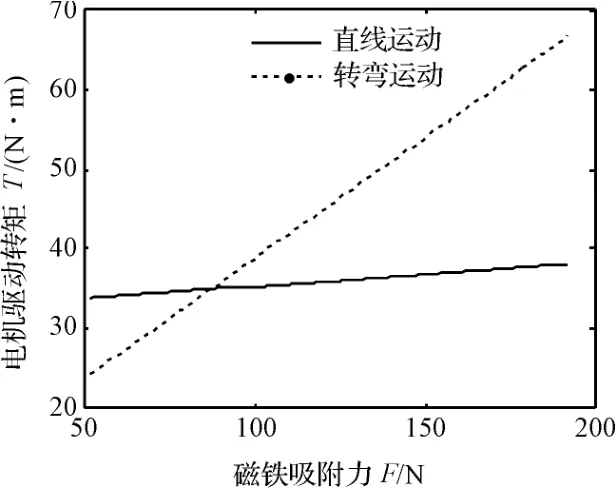
图6 磁铁吸附力与电机所需驱动转矩的关系

4 结束语

本研究对永磁吸附履带式爬壁机器人进行了受力分析。首先根据履带式爬壁机器人特点，重新定义了载荷分布系数，然后对爬壁机器人进行静力学分析，建立了数学模型，并根据现有爬壁机器人硬件参数进行仿真，确定了机器人在不同的壁面倾角和载荷分布系数下，单个磁铁所需要的最小吸附力和单个电机所需要的最小转矩。根据仿真结果，确定通过提高载荷分布系数可以提高机器人在壁面运动的安全性，而且还要考虑磁铁吸附力对电机转矩的影响，才能提高机器人运动的灵活性。本研究结果为永磁吸附履带式爬壁机器人的结构优化和安全操作提供了理论支持。

［1］李志梅，付宜利，王树国．四轮驱动滑动吸盘爬壁机器人的动力学研究［J］．机器人，2010，9(32):601-607．

［2］SCHMIDT D，BERNS K． Climbing robots for maintenance and inspections of vertical structures-A survey of design aspects and technologies［J］．Robotics and Autonomous Systems，2003(61):1288-1305．

［3］衣正尧，弓永军，王祖温，等． 新型除锈爬壁机器人附壁建模与仿真［J］．四川大学学报，2011，43(3):211-216．

［4］孙 玲，弓永军，王祖温，等．船舶除锈机器人转向运动学分析［J］．机械设计与制造，2014，7(7):189-195．

［5］仝建刚，马培荪，陈俊梅．履带式磁吸附爬壁机器人壁面适应能力的研究［J］． 上海交通大学学报，1999，33(7):851-854．

［6］徐泽亮，马培荪．永磁吸附履带式爬壁机器人转向运动灵活性分析［J］．上海交通大学学报，2003，37(11):58-65．

［7］张俊强，张 华，万伟民．履带式爬壁机器人磁吸附单元的磁场及运动分析［J］．机器人，2006，28(3):219-223．

［8］黄 波，李新俊，阚玉红． 基于ADAMS 的某履带式机器人扒动性能分析［J］．兵工自动化，2014(11):41-43．

［9］衣正尧，弓永军，王祖温．新型船舶壁面除锈爬壁机器人动力学建模与分析［J］． 机械工程学报，2010，46(8):23-30．

［10］吴运耕． 试谈双履带行走装置的转弯理论和功率计算［J］．机械工程，1978(1):11-29．

［11］周 君，王殿龙，徐 伟，等．履带车辆硬地面转向阻力矩算法的研究［J］．起重运输机械，2010(5):20-23．

［12］周新建，刘祥勇．大型油罐爬壁机器人吸附结构的优化设计［J］．机械设计与制造，2014(9):181-184．

［13］岳荣刚，王少萍．一种爬壁机器人的动力学建模［J］．北京航空航天大学学报，2013，39(5):640-644．

［14］李 根，沈青青，强 华，等．球罐爬壁打磨机器人结构设计及其吸附力仿真［J］．轻工机械，2014(4):18-21．