基于短时傅里叶变换的变压器绕组故障分析

张华元

(云南电网通海供电有限公司，云南 玉溪 652700)

0 前言

频率响应分析法是一种检测电力变压器绕组变形故障快速、有效、无损的方式，具有较小的输出响应偏差及较高的故障诊断稳定性而被广泛应用。根据激励电源的性质，频率响应分析法分为正弦频率响应法(Sweep Frequency Response Analysis，SFRA)和脉冲频率响应法(Impulse Frequency Response Analysis，IFRA)［1］。其中，正弦频率响应法应用较多，已出现中国电力行业标准和IEC 标准。正弦频率响应法直接在频域实现绕组激励和响应信号的测量，并绘制频率响应曲线，因而不易受外界干扰和系统稳定性的影响，但该方法目前离线应用较多，检测速度一般，并且绕组状态评判标准多采用基于相关系数评判的中国电力行业标准，具有很大的局限性［2］。

目前对于脉冲频率响应法的应用中，激励信号和响应信号的测量在时域实现，频率响应曲线的获取，大多采用快速傅里叶变换算法［3］。然而，快速傅里叶变换 (Fast Fourier Transform，FFT)适用于处理平稳信号，对暂态信号的时频转换容易造成频谱泄露和栅栏现象等缺陷［4］。因此，有必要开展适合处理暂态信号新的时频分析方法以获得脉冲频率响应曲线。

本文提出以短时傅里叶变换算法(Short Time Fourier Transform，STFT)处理暂态信号，以期获取正确的绕组脉冲频率响应图谱，通过理论推导、仿真验证和试验验证，该方法能够提高脉冲频率响应法在线应用与绕组状态评估的准确性。

1 基本原理

短时傅里叶变换中，短窗宽能够提供较好的时域解析度，长窗宽能够提供较好的频域解析度，根据Heisenberg 不确定性准则，短时傅里叶变换的时域解析度和频域解析度不能同时达到最优，这就限制了它的应用［5］。但由于本文的重点是正确获取绕组脉冲频率响应曲线，获取曲线的前提是获得信号精确频率分布，只要能够在保证足够频率分辨率的同时，考虑一定的时域分辨率，即能不失真地获得绕组脉冲频率响应曲线，又能消除采用快速傅里叶变换带来的缺陷［6］。

信号x (t)的连续短时傅里叶变换定义如式(1)，其中ω 其中ω 是窗函数:

信号x (n)的离散短时傅里叶变换定义如式()，实际上，离散形式是连续的一种采样形式。

假定脉冲频率响应分析法中的激励电压信号Vin (t)和响应电压/电流信号Rout (t)的短时傅里叶变换分别由Vin (里叶变换和Rout (叶变换分别表示，根据边际谱的定义，则脉冲频率响应曲线可由下式(3)获得。

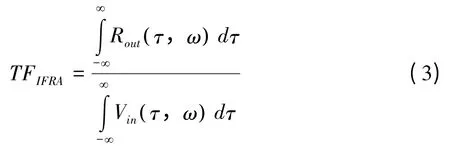
离散形式如式(4)所示:

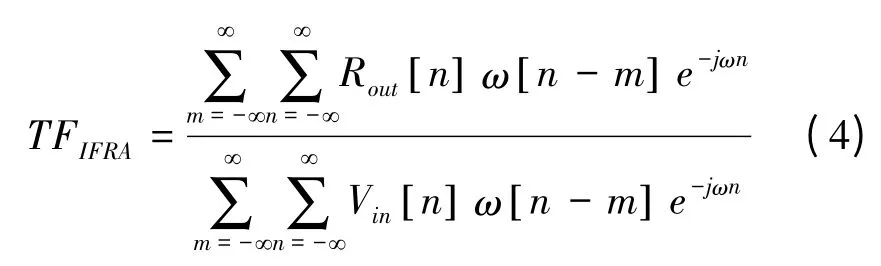
2 仿真验证

为了验证本文提出方法的可行性，建立了一个变压器单绕组的等效电路模型，该绕组由67 饼构成，R、L 和C 构成的单饼等值电路模型如图1 所示。

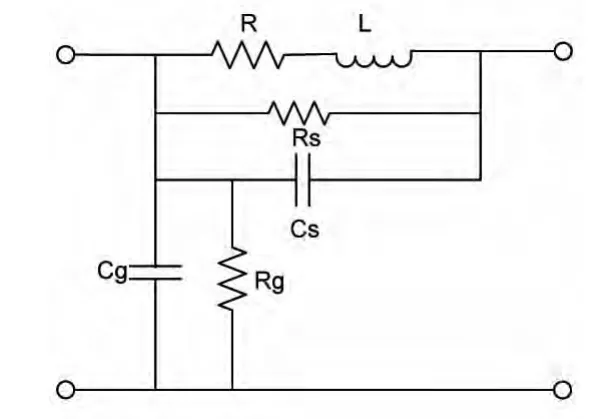
图1 模拟型变压器

本文将Matlab 软件和Pspice 软件相结合，利用Pspice 进行电路瞬态仿真，利用Matlab 进行数据后处理。

需要注意的是，Pspice 软件的瞬态分析采用了变步长的方法以减小累积误差，这在Matlab 数据后处理时无法获取等间隔的采样数据，因此，在进行时频转换前，本文采用了三次样条插值的方式，从Pspice 仿真结果获取等间隔采样数据。为了检验本文提出方法的可行性，仿真时对绕组等效电路模型进行了扫频分析，获取绕组的正弦频率响应曲线;数据处理同时采用了传统的FFT变换，进行短时傅里叶变换时采用Hamming 窗，最后将三种结果进行对比，具体仿真流程如图2所示。

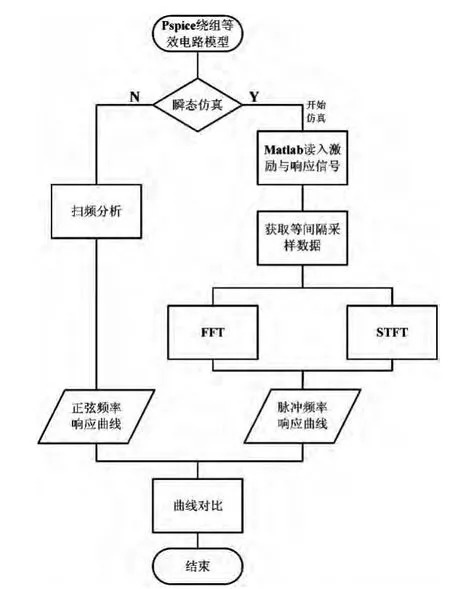
图2 仿真分析流程图

进行脉冲注入绕组的仿真分析时，脉冲参数选择接近实际试验使用的10 ns 前沿、10 ns 后沿、500 ns 脉宽、500 V 幅值的方波脉冲，脉冲频率响应曲线由注入绕组首端的激励电压信号和响应电流信号构成。

采用本设计提出的基于短时傅里叶变换的脉冲频率响应曲线获取方法处理上述数据，结果如图3－图5 中的(a)所示，图中还显示了FFT 算法处理的结果。为了更直观的展现包括正弦频率响应分析法01MHz 频段的低频部分频率响应曲线的走势和谐振点信息，采用绕组等效电路导纳参数作为频率响应曲线的纵轴，横轴频率取为05MHz，分析结果如图3－图5 中(b)所示，其中蓝色、绿色和红色曲线分别表示A、B 和C 三相绕组脉冲频率响应曲线。

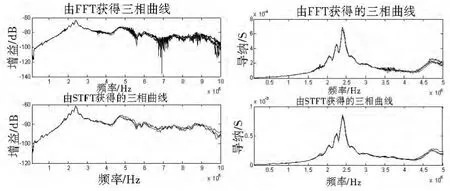
图3 Y 形连接中性点接地下三相试验曲线对比图

图4 Y 形连接中性点不接地下三相试验曲线对比图

从图3－图5 中可以看出，经过STFT 变换处理后的脉冲频率响应曲线主要谐振点的信息未丢失，特别是反映绕组各种变形故障的频段，在保留基本谐振点信息的同时几乎不受噪声影响，有利于根据频率响应曲线判断绕组的变形状况。

参考中国电力行业标准DL/2004，采用相关系数数学指标评估两个频率响应曲线的相似程度，两个转移函数序列X (k)和Y (k)，k=0，1 系数数学的标准偏差定义如下式(5)和(6)。

图5 三角形连接下三相试验曲线对比图

序列的协方差定义如下式(7):

序列的归一化协方差系数如下式(8):

相关系数定义为式():

对FFT 和STFT 变换的结果分别进行处理，依据DL/2004 频段划分标准在01 范围内计算两相曲线之间的相关系数，如下表1 所示。从表中可以看出，STFT 处理后的两相绕组间的相关系数均大于4，明显大于FFT 处理后的相关系数。根据试验设置可知，大修后的变压器三相绕组健康状态良好，结构一致，频率响应曲线应尽可能相似。因此，本文提出的基于STFT 的变换方法优于FFT 算法，更适合处理暂态信号，从而获取绕组正确的脉冲频率响应曲线。

表1 不同数据处理方式下相间曲线数据对比(Y 形连接跃居第一 点接地)

另外，需要说明的是，经过STFT 处理后的三相频率响应曲线在02 频段差异较小，随着频率的增加，曲线差异明显变大，且较FFT 处理的结果更清晰。将频率响应法的检测频段提高至10，可以检测绕组的微小变形，结合本文测试结果，由于频响曲线的高频段对绕组的微小变形较为灵敏，变压器的三相健康绕组结构一致，相间绕组的微小差异即在频率响应曲线的高频段体现出来。

3 结束语

本文提出采用短时傅里叶算法构建变压器绕组的脉冲频率响应曲线，采用Pspice 软件建立了单绕组等效电路模型并进行暂态时域仿真，通过仿真分析可知，经过短时傅里叶算法处理后，频率响应曲线清晰度高，噪声较小，频响曲线更接近实际情况，通过测试结果可以看出，高频段曲线变化对绕组的微小变形较为灵敏变压器相间绕组的微小差异即在频率响应曲线的高频段体现出来，因此本文提出的方法可以快速准确的诊断变压器故障。

［1］郭创新，朱承治，张琳，等.应用多分类多核学习支持向量机的变压器故障诊断方法［J］.中国电机工程学报.2010 (13).

［2］杨廷方，李景禄，曾祥君，等.基于多方法组合诊断模型的大型变压器故障诊断［J］.电力系统自动化，2009(20).

［3］颜秋容，刘欣，尹建国.基于小波理论的电力变压器振动信号特征研究［J］.高电压技术，2007 (01).

［4］汲胜昌，王世山，李清泉，等.用振动信号分析法监测变压器绕组状况［J］.高电压技术，2002 (04).

［5］汲胜昌，李彦明，傅晨钊.负载电流法在基于振动信号分析法监测变压器铁心状况中的应用［J］.中国电机工程学报，2003 (06).

［6］王璋奇，王孟.电力变压器绕组轴向振动稳定性分析［J］.中国电机工程学报，2002 (07).