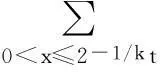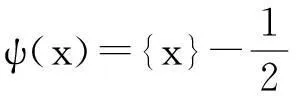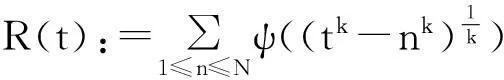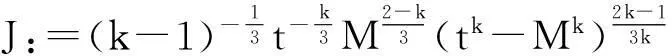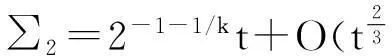Lamé曲线内整点个数

彭道意，刘　浩

(1.湖北师范学院文理学院， 湖北 黄石 435002； 2.湖北师范学院数学与统计学院, 湖北 黄石 435002)

Lamé曲线内整点个数

彭道意1，刘浩2

(1.湖北师范学院文理学院， 湖北 黄石 435002； 2.湖北师范学院数学与统计学院, 湖北 黄石 435002)

摘要：利用 Euler-Maclaurin 求和公式与 van der Corput 定理, 初步研究了 Lamé 曲线内的整点个数, 给出了相应的渐进公式.

关键词：Lamé曲线；整点；Euler-Maclaurin求和公式；van der Corput定理；指数和

Euclid 空间上指定区域内的整点(格点)问题, 是解析数论中重要的问题之一. Gauss 圆问题与 Dirichlet 除数问题是典型的未解决的整点问题，多位学者研究过此类问题, 发展了诸多方法, 如Weyl指数和估计、指数对理论、多变量 van der Corput方法、广义Bessel函数理论等[1-8].

对Pk(t)的估计，已有大量研究[7]. 本文使用经典的van der Corput方法, 不同于Krätzel等[8]引进的广义Bessel函数方法, 给出了Pk(t)的渐进估计.

1记号与引理

若x∈R，⎣x」表示不超过x的最大整数，{x}为x的小数部分. 函数ψ(x).记e(z)∶=e2πiz，z∈C.自然对数记作logx. Riemann zeta函数为C.

对于给定的实变量或复变量函数f,g，本文将不加区别地使用Landau记号f=O(g)或Vinogradov记号f≪g来表示存在一个正常数C使得在f与g的公共定义域内有|f|≤C|g|.该常数可以是绝对常数，也可以依赖于某些参数k,l,…，此时用f=Ok,l,…(g)或f≪k,l,…g表示.

为计算Pk(t)，需要如下引理.

引理1(Euler-Maclaurin 求和公式)设f∈Ck([a,b])，对整数1≤m≤k有

其中Br(x)是Bernoulli多项式.

证明参见[9]中定理9.2.2，或[10]第一部分第0章定理4、[11]第4章定理4.2.有关Bernoulli多项式的概念在[9]中第9章做了详细介绍，同样见[10]第0章或[11]第4章第2节.

引理2 (van der Corput)令a,b∈R，a

证明参见[6]定理2.2, [10]第一部分第6章定理5，或[11]第8章推论8.13.

引理3∀J≥1，x∈R，b-a=I，有其中αj≪min(j,J)/j2.

证明参见[8]中定理1.8，或参考[6]中引理4.3和定理A.6，这基于文献[12].

引理4令α∈C{-1}，对任意的k>R(α)+1，使得k≥1，有,其中,且有t.

证明参见文献[9]中命题9.2.13.这里对Riemann zeta函数作了解析延拓.

由引理 4，计算可得如下结果:

推论1

ζ(1/2)≈-1.460 4,ζ(3/2)≈2.612 4.

2主要结果

证明Lamé曲线|x|k+|y|k=tk(k≥2)是中心对称图形，在直角坐标系内关于直线y=±x对称，易得

(1)

其中

(2)

下面将分别对∑1, ∑2作出估计.

(3)

(4)

记

(5)

考虑函数g(x)=j(tk-xk)1/k, 求导得

g′(x)=-jxk-1(tk-xk)-1+1/k,

g″(x)=-j(k-1)tkxk-2(tk-xk)-2+1/k,

g‴(x)=-j(k-1)tkxk-3(tk-xk)-3+1/k((k-2)tk+(k+1)xk),

因为|g″(x)|为[0,2-1/kt]上的单调递增函数.由引理2, 对M

结合引理3，可得

上面对j的求和用到了推论1，以及ζ(1/2)=O(1)，ζ(3/2)=O(1).

令r0=⎣logN/log 2」-1，则有2r0+1≤N≤2-1/kt，由式(5)可得

从而由式(4)即得

(6)

将式(3)，(6)代入(2)，再结合式(1)，定理1得证.

参考文献:

[1] Huxley M N. Exponential sums and lattice points III[J]. Proceedings of the London Mathematical Society,2003,87(3):591-609.

[2] Huxley M N. Area, lattice points, and exponential sums[M]. Oxford: Oxford University Press,1996.

[3] Soundararajan K. Omega results for the divisor and circle problems[J]. International Mathematics Research Notices,2003(36):1987-1998.

[5] Tsang K M. Recent progress on the Dirichlet divisor problem and the mean square of the Riemann zeta-function[J]. Science China Mathematics,2010,53(9):2561-2572.

[6] Graham S W， Kolesnik G. Van der Corput’s method of exponential sums[M]. Cambridge: Cambridge University Press,1995.

[8] Erätzel E. Lattice points[M]. Dordrecht-Boston-London: Kluwer Academic Publishers,1988.

[9] Cohen H. Number theory volume II: analytic and modern tools[M]. New York: Springer, 2007.

[10] Tenenbaum G. Introduction to analytic and probabilistic number theory[M]. Cambridge: Cambridge University Press,1995.

[11] Iwaniec H， Kowalski E. Analytic number theory[M]. Providence: American Mathematical Society,2004.

[12] Vaaler J D. Some extremal functions in Fourier analysis[J]. Bulletin of the American Mathematical Society,1985,12(2):183-216.

The Number of Lattice Points in Lamé Curve

PENG Daoyi1, LIU Hao2

(1.College of Art and Science，Hubei Normal University, Huangshi 435002, China； 2.School of Mathematics and Statistics,

Hubei Normal University, Huangshi 435002, China)

Abstract:Using Euler-Maclaurin summation formula and van der Corput Theorem, this paper preliminary studies the number of lattice points in Lamé curve, and provides the relevant asymptotic formula.

Key words:Lamé curve; lattice points; Euler-Maclaurin summation formula; van der Corput Theorem; exponential sums

文章编号:1674-232X(2015)06-0659-04

中图分类号:O156.4MSC2010: 11P21

文献标志码:A

doi:10.3969/j.issn.1674-232X.2015.06.018

通信作者：刘浩 (1978—), 男, 讲师, 博士, 主要从事非线性泛函分析研究.E-mail:liuhao.whu.nlsc@163.com

基金项目：湖北师范学院文理学院大学生科研项目(DK201416).

收稿日期：2015-04-15