降维的对偶忆阻混沌电路及其FPGA的实现

詹信雄，许碧荣，黄　聪，邱　蓉，刘志国

(武夷学院机电工程学院，福建 武夷山 354300)

降维的对偶忆阻混沌电路及其FPGA的实现

詹信雄，许碧荣，黄聪，邱蓉，刘志国

(武夷学院机电工程学院，福建 武夷山 354300)

摘要：提出了一个对偶忆阻器混沌电路，对其降维研究的结果表明降维的对偶忆阻混沌电路与对偶蔡氏混沌电路一致.并利用FPGA实现了降维的忆阻混沌电路，说明此忆阻混沌电路可数字化实现.

关键词：忆阻器；对偶；混沌电路；降维；FPGA

0引言

1971年Chua从理论上说明了忆阻器的存在[1]，但由于当时现实中不存在此类元件，所以没有引起科学界和工程界的重视，直到2008年HP实验室制作出了实际的纳米级忆阻器[2]，证明了忆阻器的存在，才引起了学界的广泛兴趣.由于忆阻器是一种无源的非线性电路元件，有着潜在的应用前景，常被用于混沌电路的设计[3-5]，而由忆阻器构造的混沌系统的维数较高.因此，本文提出了一个对偶忆阻器混沌电路，并对其降维研究，然后利用FPGA将降维忆阻器混沌电路数字化实现.

1忆阻混沌电路的建模

1.1　对偶忆阻混沌电路

通过荷控忆阻器替换对偶蔡氏电路[6]的蔡氏二极管，得到的电路如图1所示，其中M为一个忆阻器.

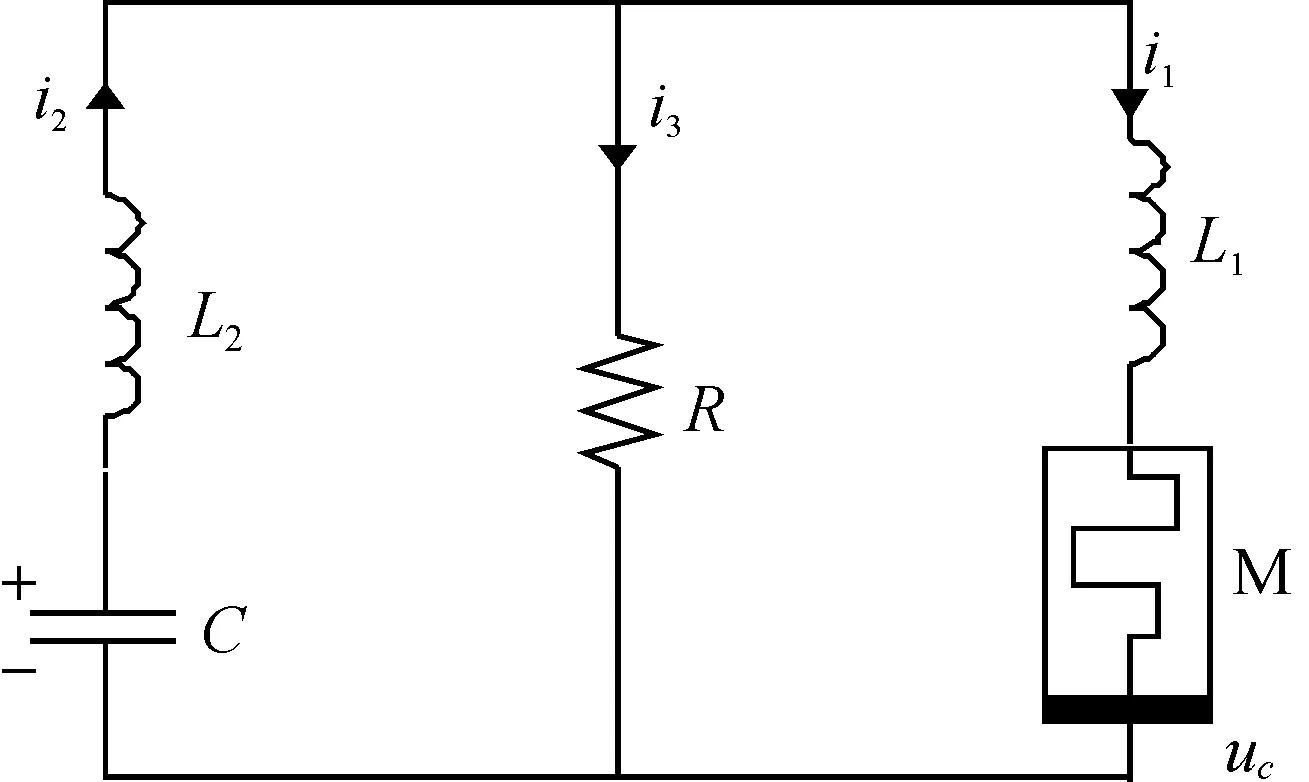
图1　对偶蔡氏忆阻混沌电路Fig. 1　A dual Chua’s memristive chaotic circuit

荷控忆阻器用一个光滑的三次单调上升的非线性函数描述，即

φ(q)=aq+bq3.

(1)

式中φ表示磁通，q表示电荷，a>0，b>0.相应的，荷控忆阻器的忆阻W(q)为

(2)

1.2　对偶忆阻混沌电路的建模

荷控忆阻器是一个动态元件，其状态变量为电荷q，其他的3个动态元件电感L1、电感L2和电容C对应的状态变量分别为电流i1、电流i2和电压uc.根据图1所示的电路，运用基尔霍夫电流和电压定律以及元件伏安关系，得到了定义状态变量i1、i2、uc和q之间关系的4个联立的一阶微分方程，即

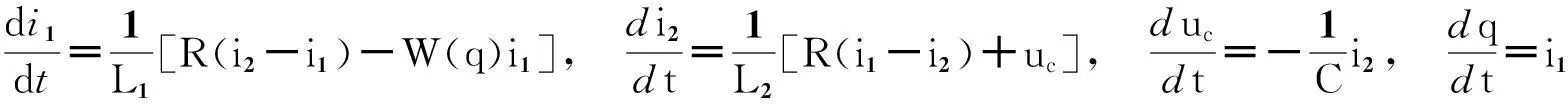
(3)

设x=i1，y=i2，z=uc，ω=q，α=1/L1，β=1/C，L2=1和R=1，状态方程(3)可以重写为

(4)

这表明对偶忆阻混沌电路是一个四维系统.

系统(4)有一个平衡点集合E={(x,y,z,ω)|x=y=z=0,ω=c},即ω坐标上的点集均是平衡点，其中c是一个实常数.

1.3　降维的对偶忆阻混沌电路

根据基尔霍夫电流定律和基尔霍夫电压定律可列出图1中两个环路的电压方程分别为

(i2-i1)R-uL1-uM=0，

(5)

uL2+(i2-i1)R-uc=0，

(6)

式中uL1,uL2和uc分别表示电感L1、电感L2和忆阻M两端的电压.

利用文献[7]的方法，对式(5)、(6)的两边进行积分，并根据电感和电容的元件特性关系，可得以电荷q1、电荷q2和磁通φuc为状态变量的微分方程：

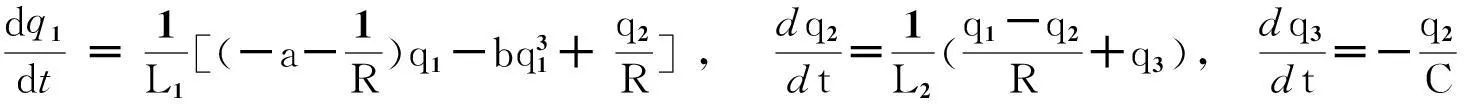
(7)

令x=q1,y=q2,z=q3,α=1/L1,β=1/C,L2=1和R=1，式(7)的状态方程可重写为

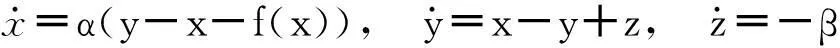
(8)

式中f(x)=ax+bx3.

与系统(4)相比，很明显系统(8)在维数上降了一维，变成了一个三维系统，同时从系统(8)的方程形式，可以看出该系统是一种光滑的对偶蔡氏混沌系统.

2降维忆阻混沌电路的FPGA实现

以下用FPGA技术来实现此降维忆阻混沌电路.实现此电路采用的是Altera公司开发的quartus II和DSP builder，该软件开发平台的特点是能直接利用simulink来调用DSP Builder库中的各个单元，便于电路模块化设计和FPGA硬件的实现.

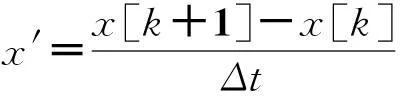
x[k+1]=x[k]+Δtα(y[k]-x[k]-ax[k]-bx3[k])，

y[k+1]=y[k]+Δt(x[k]-x[k]+z[k])，

(9)

z[k+1]=z[k]+Δtβy[k].

在MATLAB的simulink中，利用DSPBuilder库中的单元模块搭建数字电路，如图2所示.

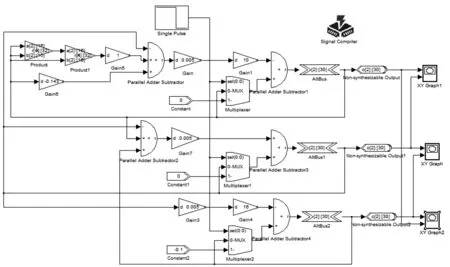
图2　基于DSP Builder平台搭建的电路模型Fig. 2　The circuit model based on DSP Builder platform

在DSP builder中仿真，参数a=-0.143，b=1，α=10,β=16，τ=0.005，初始条件为{0,0，-0.1}时，其相位图如图3-图5所示.由图中可清楚地看到，当此电路参数满足一定条件时，会产生像蔡氏电路一样称为双漩窝的自激振荡吸引子，这是整体稳定和局部不稳定相结合的产物，混沌轨道则是在奇怪吸引子上盘旋运行的流.

图3　x-y平面的双漩涡混沌吸引子Fig. 3　Dual whirlpool chaosattactor on x-y plane

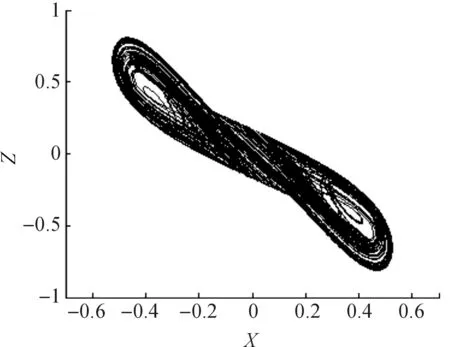
图4　x-z平面的双漩涡混沌吸引子Fig. 4　Dual whirlpool chaosattactor on x-z plane

图5　y-z平面的双漩涡混沌吸引子Fig. 5　Dual whirlpool chaosattactor on y-z plane

为了用FPGA技术实现系统(9)，接着利用DSP builder创建一个MDL文件，经仿真验证满足设计需要后，经信号编译器将MDL文件转换为VHDL文件和QPF文件，再对QPF文件进行分析、综合和编译，通过JTAG端口将代码下载到FPGA芯片中，经A/D 转换器，将FPGA输出的数字信号转换成模拟信号，用示波器观测记忆电阻蔡氏混沌电路中的混沌吸引子，其结果和仿真实验结果一致.

3结论

本文提出了一种对偶忆阻混沌电路，并对其降维处理，揭示了对偶忆阻混沌电路和对偶蔡氏混沌电路的关系，并用FPGA很好地实现了降维的对偶忆阻混沌电路.

参考文献:

[1] Chua L O. Memristor-the missing circuit element[J]. IEEE Transactions on Circuit Theory，1971，18(5)：507-519.

[2] Strukov D B， Snider G S， Stewart D R，etal. The missing memristor found[J]. Nature，2008，453：80-83.

[3] 包伯成，刘中，许建平.忆阻混沌振荡器的动力学分析[J].物理学报，2010，59(6)：3785-3789.

[4] 许碧荣.一种最简的并行忆阻器混沌系统[J].物理学报，2013，62(19)：190506．

[5] 包伯成，王其红，许建平.基于忆阻元件的五阶混沌电路研究[J].电路与系统学报，2011，16(2)：66-69.

[6] 刘崇新.蔡氏对偶混沌电路分析[J].物理学报，2002，51(6)：1198-1202.

[7] 包伯成，王春丽，武花干，等.忆阻电路降维建模与特性分析[J].物理学报，2014，63(2)：020504.

A Dual Memristive Chaotic Circuit of Dimensionality Reduction and

its FPGA Realization

ZHAN Xinxiong, XU Birong, HUANG Cong, QIU Rong, LIU Zhiguo

(School of Mechanical and Electrical Engineering, Wuyi University, Wuyishan 354300, China)

Abstract:In this paper, a dual memristive chaotic circuit is presented. Its dimensionality reduction is studied, and it is obtained that the dual memristive chaotic circuit of dimensionality reduction is consistent with the Chua’s dual chaotic circuit. Then, FPGA is used to implement this chaotic circuit, and it expresses that the memristive chaotic circuits can be realized by digital way.

Key words:memristor; dual; chaotic circuit; dimensionality reduction; FPGA

文章编号:1674-232X(2015)06-0656-03

中图分类号:TN918

文献标志码:A

doi:10.3969/j.issn.1674-232X.2015.06.017

通信作者：许碧荣(1973—)，男，教授，主要从事非线性电路理论及应用研究.E-mail：xubirong1@163.com

基金项目：福建省自然科学基金项目(2012D127)；福建省教育厅科技项目(JA11264)；国家大学生创新创业训练计划项目(201310397015).

收稿日期：2015-05-12