浅谈如何强化中学数学的教与学
江苏省新沂市马陵山中学 盛 菲
当前世界处于科学技术飞速发展的状态,知识成倍增加,数学的情况尤为突出.怎样适应这一新形势的要求,使学生多快好省地不断掌握现代数学知识,已十分尖锐地摆在教师们的面前.
一、要让学生明确学习数学的重要性与自觉性
不少学生升入中学后数学成绩会退步,原因固然涉及到方方面面,但与学生没有明确学习数学的重要性与自觉性有一定关系.因此,让学生明确学习数学的重要性与自觉性就成为首要问题了.为此,一是通过最佳的途径学习最佳的数学,从整体化观点来看,这并不是没有可能的;二是提高能力,发展智力,交给学生一把钥匙,以打开数学的大门,而学习数学可以有利于学生达到自己的目标.
近几十年来,国际上掀起了数学教育现代化运动的高潮,就是为适应这种需要而产生的.数学本身就是一门非常重要的学科,同时又是学好其他理科知识的基础.数学学不好,就会影响其他学科的学习和发展,从而会影响学生进一步升学和就业.所以,数学学科是非常重要的,学生应该增强学习数学的自觉性.
学生从小学进入初中以后,将要学习很多数学知识,代数、几何、不等式等.有少部分知识他们在小学时略有接触,但大部分知识都是新的.而中学阶段的数学对学生又提出了新要求,不仅要掌握知识,更要提高能力,尤其要领会数学思想方法.在各种数学知识中,它们都不是孤立的,而是相互联系着的,有些知识是可以相互转化的,如数与形的转化.
在教学中,给学生介绍一些数学方法是很有必要的.如各种推理方法.但必须注意,不完全归纳法推出的结论既可能真,也可能假.因此,使用不完全归纳法进行推理是不严格的,但是它在科学研究中具有巨大的价值和意义,在解题中便于发现规律,启发思维.演绎推理表现形式是:集合M 中的元素具有(或不具有)P,x∈M,x 也具有(或不具有)P.例如,因为负数无对数(大前提),-1是负数(小前提),所以,-l无对数(结论).类比推理虽然有它的缺点,但仍不失为一种获取新知识的工具.但是,我们应防止乱用类比推理而造成错误.例如,有的学生误将logα(x+y)、sin(x+y)与a(b+c)进行类比,造成下列错误:logα(x+y)=1ogαx+1ogαy sin(x+y)=sin x+sin y.
二、要让学生认识学习数学的迫切性与针对性
进入21世纪以来,我国中学数学教学的情况有了根本性的好转.但是由于多方面的原因,应试教育严重,素质教育远远没有落到实处.老师讲风太盛,学生学得不到位.很多老师没有掌握数学教育规律,因此普及数学知识已成为当前十分紧迫的任务.
学生进入初中以后,他们接触的代数、几何、不等式等的概念、定义等很多.在给学生讲清了概念和定义之后,应该让学生通过解题来加强运用.学习概念、定义及有关定理和解题方法,只是一种手段,运用才是目的.如学习了数学中的分析法与综合法后,就可以让学生做如下练习:

三、要让学生体会学习数学的长期性与艰巨性
数学是基础学科,要想在短期内学好数学是不可能的.数学学习具有长期性和艰苦性的特点,我们的学生必须清楚地了解这一点.另外,学习数学除了掌握必要的概念、定义、公理等外,必须大量地做练习,只有通过大量地做练习,才能巩固所学的数学知识.
如证明题在初中数学中大量出现,证明方法很多.下面举一反证法的例子.
求证:cos10°是无理数.
证明:假设cos10°是有理数,记cos10°(p、q 为互质数),则cos30°=4cos310°-3cos x=4是一有理数.而是一无理数,这样与已作假设相矛盾,故cos10°是无理数.
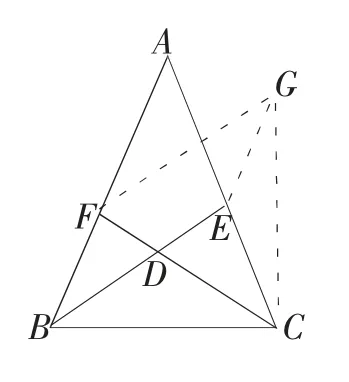
再如,如图所示,在△ABC 中,已知BE 和CF 分别是∠ABC 与∠ACB 的平分线,且BE=CF,求证:AB=AC.
证 明:如 果AB≠AC,那么,就有AB>AC 或AB 则∠ACB<∠ABC(自相矛盾), 即AB>AC 不可能. 同理可证,AB<AC 的情况是不可能的.∴AB=AC. 大量的教育实践经验既迫切需要上升到理论,也迫切需要正确理论的指导.应该看到,当前我国数学教学还比较落后,教学理论贫乏,教材陈旧,教学手段尤其是农村还比较简陋,数学教育工作者的整体科学修养还比较差,需要重新学习,更需要我们不断实践,不断探索.因此,根据数学教育科学的特点与现状,学习与研究数学是一个长期而艰巨的任务.