基于领结模型和半马尔科夫的变压器故障率预测及研究*

沈 鑫，曹 敏，高文胜，王 昕，刘清蝉*

（1.云南电网公司电力科学研究院，昆明 650217；2.清华大学电机系，北京 100084）

变压器是电力系统最昂贵和重要的设备，其可靠、稳定的运行状态对电网起着至关重要的作用，变压器一旦发生故障，将会对电力系统的安全运行带来重大影响。因而，对变压器运行状态进行可靠、准确、及时的评估具有非常重要的意义。基于准确全面的变压器故障模型进行故障率分析判断是变压器故障预防和寿命管理的主要手段之一。变压器的故障可分为劣化故障和随机故障，劣化故障是因性能逐渐劣化而导致的故障，如热老化；随机故障是指因随机因素导致的故障，如人为因素、雷击等。

领结模型和马尔科夫链是设备可靠性分析中常用的有力工具，已有学者基于马尔科夫过程建立了变压器的故障预测模型。IEEE准则中基于油中溶解气体的体积分数将变压器划分为四个状态［2］，文献［3-4］利用这4个状态建立了马尔科夫模型，得到了变压器故障率的变化趋势，但此类模型没有考虑各种随机故障；另外，油中溶解气体划分的状态对应多种故障模式，没有代表性，实际应用十分困难，不确定度很大。传统马尔科夫过程要求状态的停留时间必须服从指数分布，在实际工程中，变压器的故障过程多种多样，很难采用传统模型。半马尔科夫过程是马尔科夫过程的扩展模型，没有要求指数分布类状态停留时间的限制，可任意分布，从而使应用于变压器的实际故障过程。

本文采用国内、外变压器故障统计数据进行分析结果，利用领结模型和半马尔科夫过程建立了包含老化故障和随机故障过程的故障模型，通过算例分析确定模型中参数的取值，所得结果克服了马尔科夫过程模型的不足，与实际的变压器故障率曲线相符，研究成果应用于国家863项目（2011AA05A120）。

1 变压器故障原因统计

果，可以发现输变电设备的主要故障原因包括：设计/制造/工艺因素、不良工况、老化和人为原因。基于故障原因的特点，将其划分为3类，设计/制造/工艺造成的隐患在输变电设备投运时就存在，称之为固有故障隐患；老化通常为输变电设备在工作应力作用下的劣化结果，不良工况产生的随机应力为输变电设备在运行环境中所遭受的主要诱因；人为因素指在输变电设备操作、维修等过程中人为带入的运行风险隐患。

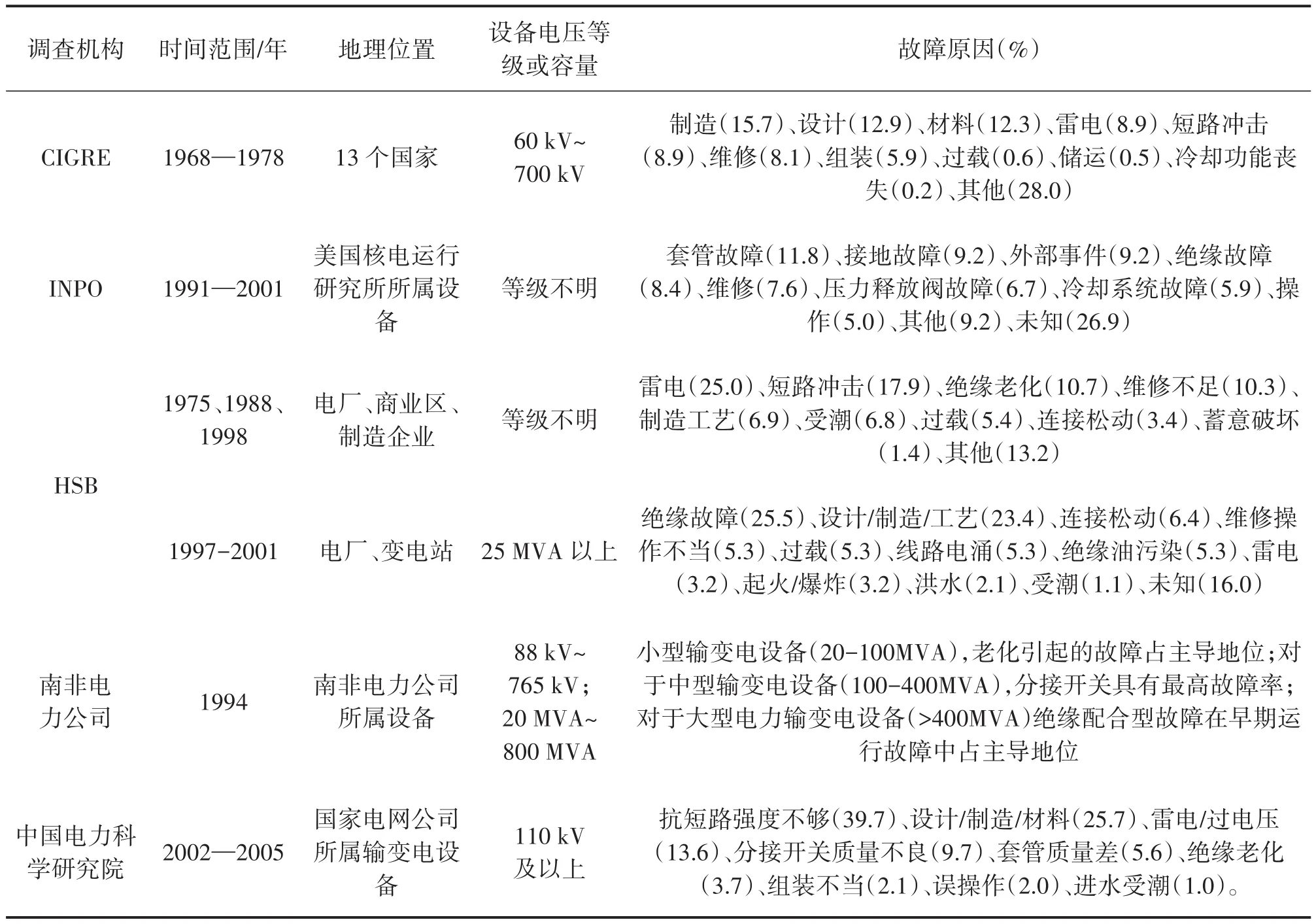
表1 故障原因统计

2 基于领结模型和半马尔科夫过程的变压器故障模型

以风险控制为导向的风险动态预警需要对故障模式同时进行向前向后的分析。本节应用领结模型BT（Bow Tie），结合故障树和事件树分析方法，分析常见故障模式的原因及后果，形成以故障模式为中心节点的领结模型，在此基础上进行风险预测。领结模型用图形的方式来描述一个关键事件的原因和结果，如图1所示，关键事件位于图形的中间，左侧用故障树分析关键事件的原因，右侧用事件树分析关键事件可能造成的后果。

传统的输变电设备故障树和事件树都可以用因果网络图表示，通过结果的前向分析和原因的后向分析可形成故障模式的领结模型。

图1 领结模型结构示意图

半马尔科夫过程与马尔科夫更新过程有关，马

尔科夫更新过程中，如n为非负整数，设X={Xn}，Xn∈S，T={Tn}，Tn≥0，且 0=T0≤T1≤…＜Tn-1≤Tn≤…。若对于任意n≥0，j∈S，t≥0满足：

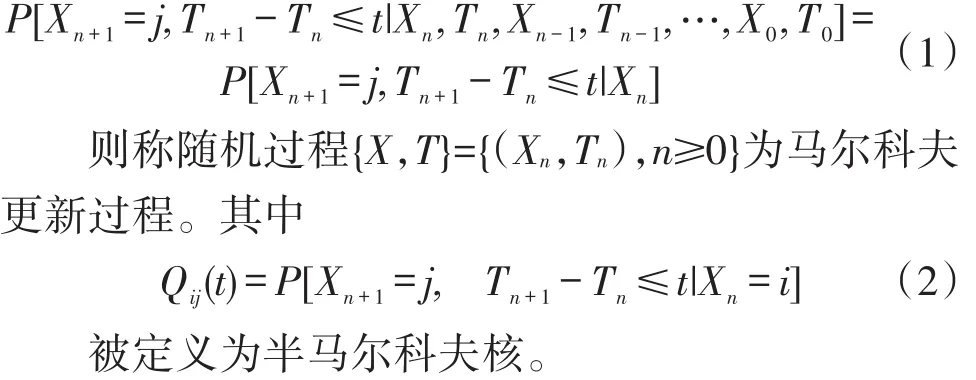
若{X，T}={（Xn，Tn），n≥0}为马尔科夫更新过程，则Yt：=Xn，t∈［Tn，Tn+1］即为半马尔科夫过程。半马尔科夫过程对状态停留时间的分布没有要求，可以为任意分布，当其为指数分布时，半马尔科夫过程就是连续时间的马尔科夫链。

获取故障概率的核心是量化关键事件与领结模型左侧原因节点和右侧后果节点间的概率关系，首先需要对领结模型左侧和右侧的结构进行简化。图2描述了领结模型化简后的基本结构，更复杂的情况一般可由这两种基本结构组成。

图2 领结模型的一般化简结构

在获得领结模型的化简结构后，下一步工作是量化其中的因果关系。采用半马尔科夫过程描述其中的劣化过程，如图3所示。

假设输变电设备在劣化状态停留时间的概率密度分布为威布尔分布，由此形成了半马尔科夫过程中常见的模型形式Weibull-Markov模型，如图4所示。

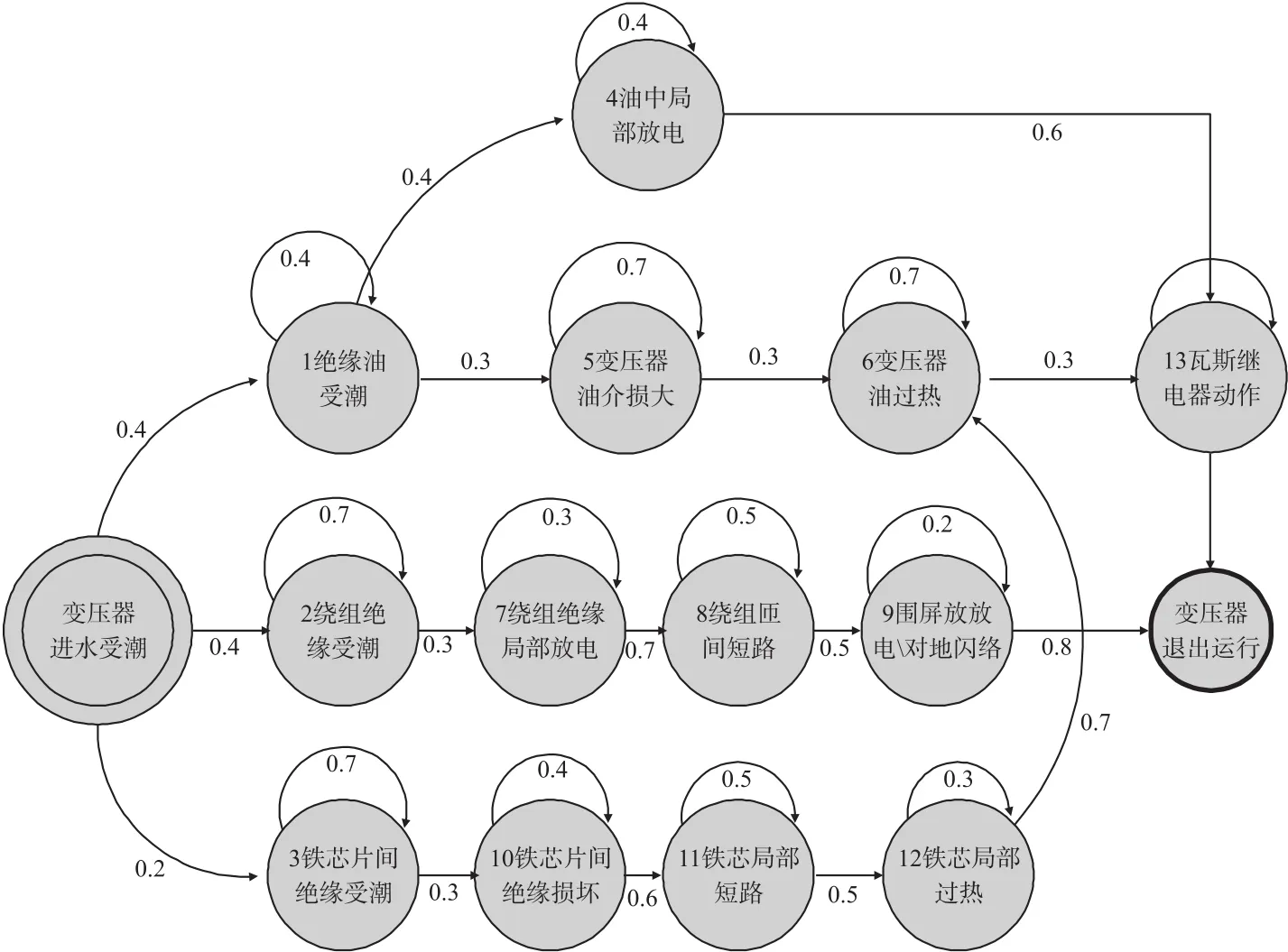
图3 变压器受潮故障马尔科夫链

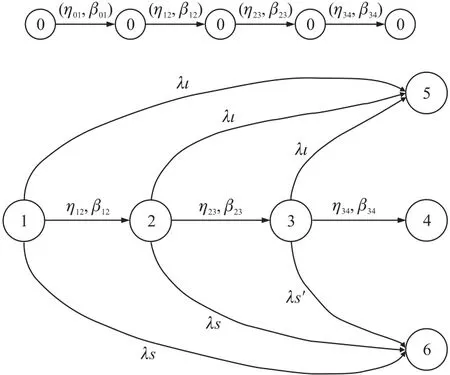
图4 半马尔科夫过程模型

在获取Weibull-Markov模型中的参数后，即可根据半马尔科夫过程的数值求解过程获取各个时刻输变电设备处于每个状态的概率，得到变压器风险中的故障概率因素。

变压器的热老化划分为从1到4共4种状态，其中状态4表示变压器老化故障状态，各个状态对应的DP值如表2所示。

形成各状态之间的转换关系如图4所示，热老化的4个状态结合由短路冲击、雷电组成的随机故障状态，形成了包含6种状态的状态空间，如表2所示。基于以下3点假设对6种状态之间的关系进行阐述：（1）热老化过程是渐进的过程，不会发生跳跃变化；（2）每个正常运行的状态（1、2、3）都可能因为各种随机因素的影响直接从运行变为故障状态；（3）变压器的故障过程不可逆，即不考虑人为修复过程。

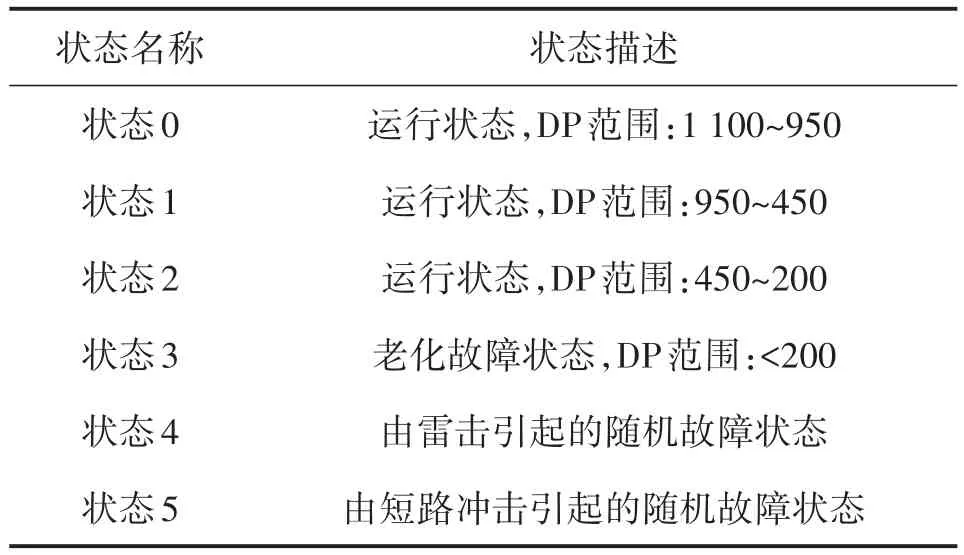
表2 状态的划分

根据文献［14-15］提出的DP和t的经验公式：

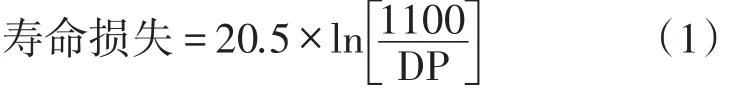
计算得到平均转移时间分别为3年、15.3年、16.6年。

3 结果分析

3.1 威布尔分布参数选取

第2节获得了3个威布尔分布的平均值：3、15.3、16.6年，表3列出了具有代表性的4个算例对应的威布尔参数，根据半马尔科夫过程模型求得的相应可靠性参数的变化曲线如图5所示。图5中的老化率是指工作到某一时刻尚未故障的变压器（处于状态1、2或3），在该时刻后，单位时间内发生老化故障（转移至状态4）的概率。实际计算方法为将单位时间步长内处于状态4的概率的增量除以前一时刻处于状态1、2、3的概率之和。故障率是老化率与随机故障率之和。

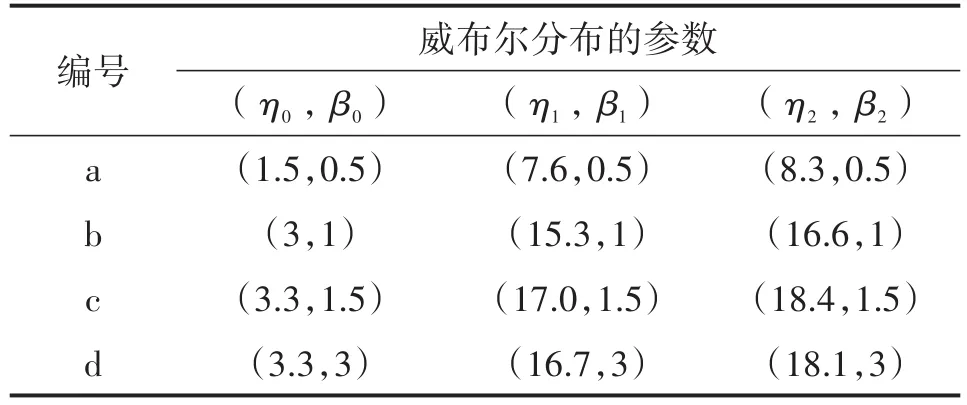
表3 算例的参数设置

图5 4个算例的计算结果

在图5中，4种参数条件下的可靠度均随时间下降，与经验相吻合，但是曲线的形式各不相同，这是由于故障率随时间的变化各不相同。算例a（β=0.5）的故障率在运行之初陡然上升到最大值，之后逐渐下降，结合其老化率与随机故障率曲线可知，主要因为老化率刚运行时的迅速上升导致了故障率的陡然上升，之后老化率与随机故障率均逐渐下降。结合所做的其它算例分析，发现β＜1时所得的线形类似，这显然与经验不符。算例b的β=1，当β=1时威布尔分布变为指数分布，此时的模型即是传统的马尔科夫过程模型。从图5（b）可以看到，基于马尔科夫过程的模型所得的故障率、老化率与随机故障率均呈凸曲线增长趋势。说明基于马尔科夫过程的模型对变压器实际运行状况的反映并不准确。继续增加β值，令β=1.5得到算例c，由图5（c）可知其故障率近似呈直线增长。可见，算例a、b与c的故障率曲线均与实际统计结果不符，另外，从图5中还可以看到，a、b、c 3个算例中老化故障率在变压器初始运行年份就存在，这也与实际情况明显不符。但是，结合b、c算例的情况可以推测，进一步加大β值，将会得到与实际统计资料趋势相符的故障率曲线。

在上述故障模式作用下，如图6所示，变压器在预测时间t=100周时以较大的概率处于状态1，在第300周时最大概率已转移至状态4，到第800周时，变压器在状态4的概率约为1，说明在第800周时变压器已确定处于故障状态。

图6 上述故障的变压器处于不同状态的概率

3.2 模型结果分析

根据3.1节的分析，威布尔分布参数β值小于1时将得到不合理的结果，等于1时转化为传统的马尔科夫模型，所得故障率虽然随运行时间增大，但是与实际统计结果的凹曲线形增长不符，随着β值的增加故障率曲线将会逐渐由凸曲线转为凹曲线。因此，取β=3时得到算例d，其可靠度、故障率、老化率与随机故障率随运行时间的变化如图5（d）所示。对比图1与图5（d）的故障率曲线可以看到，二者的基本形式一致，都呈凹曲线增长趋势。因此可以认为基于半马尔科夫的变压器故障率模型能够较好地反映实际变压器的故障机制。仔细分析两条曲线会发现其绝对值有所不同，这是由于模型采用的平均转移时间是根据实验室测得的DP经验公式计算得到的，实际变压器受到的影响因素众多，而且故障率统计中还有其他因素造成的故障，这就造成结果的不一致。对图5（d）进行分析，在变压器运行的前20年，老化率基本为0，说明这一阶段几乎不会发生老化故障，变压器故障主要由随机故障引起，平均故障率约为1.9%。这一结果与实际经验吻合。在运行20年后，老化故障呈快速增长趋势。结合第3节中模型采用的平均转移时间分析，运行之初20年内，从平均意义上讲变压器将处于状态1与2之间，由于老化是渐进的，所以这期间变压器基本不可能直接跳转到状态3老化故障，但是运行20年之后，变压器已经处于状态2，只需一步转移就发生老化故障进入状态3，因此老化率从此开始快速增长。同时，进入状态2后由于DP值小于450，造成短路冲击故障的概率增大，因此随机故障也呈现上升趋势。在运行约35年后随机故障又呈缓慢下降趋势，这是由于随机故障与老化故障存在竞争关系。由于老化过程一直存在，运行时间越长变压器老化越严重，发生老化故障的概率越大，表现在图5（d）中老化率加速上升，而模型中进入状态2后短路冲击故障的发生概率一直为常数λs'，因此其发生概率将逐渐竞争不过老化故障而发生下降，这也是本模型将来可以进一步改进之处。在运行40年时，变压器的可靠度降低到0.05左右，因此可以认为在老化故障和随机故障的共同作用下，多数变压器在40年内故障。图6中，变压器处于状态2的概率在逐渐减少，转向状态4的概率逐渐增加，而处于状态3的概率一直处于较低水平，主要因为在状态3的停留时间参数很小，平均停留时间较短。约第270周时，变压器将以较大的概率处于状态4，即很有可能处于故障状态。结合状态维修费用的分析，可得到变压器风险预测曲线呈逐渐上升趋势，可设定风险阈值，适时进行风险控制。

4 结论

本文基于现有的故障统计结果分析，建立了基于领结模型和半马尔科夫过程的变压器故障模型，包含了变压器的热老化过程和雷击、短路引起的随机故障过程。通过选取适当的参数，采用本模型能够得到与实际统计结果趋势一致的故障率曲线，而基于传统的马尔科夫过程建立的故障模型得到的变压器故障率曲线与实际不符，说明基于领结模型和半马尔科夫的变压器故障率模型能够较好地反映实际变压器的故障机制。

对模型的典型算例进行分析，得到以下主要结论：

（1）模型中的威布尔分布参数β值小于1时将得到不合理的结果，等于1时转化为传统的马尔科夫模型，所得故障率虽随运行时间增大，但是与实际统计结果的凹曲线形增长不符。随着β值的增加，故障率曲线将会逐渐由凸曲线转为凹曲线，与实际的故障率统计结果比较接近。

（2）在本文所取参数下，变压器运行前20年几乎不会发生老化故障，变压器故障主要由随机故障引起。在运行20年后，老化故障与随机故障均呈快速增长趋势。

（3）变压器在运行40年时，变压器的可靠度降低到0.05左右，可以认为，在老化故障和随机故障的共同作用下，多数变压器在运行40年内出现故障。

［1］金文龙，陈建华，李光范，等.全国110kV及以上等级电力变压器短路损坏事故统计分析［J］.电网技术，1999（6）：70-74.

［2］Pathak J，Jiang Y，Honavar V，et al.Condition Data Aggregation with Application to Failure Rate Calculation of Power Transform⁃ers［C］//Proceedings of the 39th Hawaii International Conference on System Sciences，Hawaii，2006.

［3］Velasquez-Contreras J L，Sanz-Bobi M A，Galceran Arellano S.General Asset Management Model in the Context of an Electric Utility：Application to Power Transformers［J］.Electric Power Sys⁃tems Research，2011，81（11）：2015-2037.

［4］宁辽逸，吴文传，张伯明.运行风险评估中的变压器时变停运模型（一）基于运行工况的变压器内部潜伏性故障的故障率估计方法［J］.电力系统自动化，2010（15）：9-13.

［5］Cigre.An International Survey on Failures in Large Power Trans⁃formers in Service［J］.Electra，1983（88）：21-47.

［6］Geldenhuis L，Jagers J，Gaunt T.Large Power Transformer Reli⁃ability Improvement in Eskom Distribution［C］//Proc 19th Interna⁃tional Conference Electricity Distribution，2007.

［7］Franz E N A，Bertling L.State of the Art-Life Time Modeling and Management of Transformers，Technical Report TRITA-EE 2007：041，KTH School of Electrical Engineering，2007.

［8］Lapworth J A.Transformers Reliability Surveys［Z］.Paris：CI⁃GRE，2006.20-27

［9］Wang M，Vandermaar A J，Srivastava K D.Review of Condition Assessment of Power Transformers in Service［J］.IEEE Electrical Insulation Magazine，2002，18（6）：12-25.

［10］Kawamura T，Ichikawa M，Hosokawa N，et al.Site Maintenance Operations on Oil-Immersed Transformers and The State of Re⁃newal for Low-Cost Operations in Japan［J］.CIGRE WG A2-209，Paris，France，2004.

［11］Flores W C，Mombello E，Jardini J A，et al.Fuzzy Risk Index for Power Transformer Failures due to External Short-Circuits［J］.Electric Power Systems Research，2009，79（4）：539-549.

［12］Emsley A M，Stevens G C.Review of Chemical Indicators of Deg⁃radation of Cellulosic Electrical Paper Insulation in Oil-Filled Transformers［J］.IEE Proceedings-Science Measurement and Technology，1994，141（5）：324-334.

［13］Abdelmoumene A，Bentarzi H.Reliability Enhancement of Power Transformer Protection System［J］.Journal of Basic and Applied Scientific Research，10（2）：10534-10539.

［14］Pradhan M K，Ramu T S.On the Estimation of Elapsed Life of Oil-Immersed Power Transformers［J］.IEEE Transactions on Power Delivery，2005，20（3）：1962-1969.

［15］Corradi G，Janssen J，Manca R.Numerical Treatment of Homoge⁃neous Semi-Markov Processes in Transient Case—A Straightfor⁃ward Approach［J］.Methodology and Computing in Applied Prob⁃ability，2004，6（2）：233-246.

［16］沈鑫，王昕，赵艳峰，等.基于单周控制的并网逆变器在云南电网中的研究应用［J］.电子器件，2013，36（5）：722-727.

［17］严璋，董明，孟源源.基于支持向量机及油中溶解气体分析的大型电力变压器故障诊断模型研究［J］.中国电机工程学报，2003（7）：88-92.

［18］Su Q，Mi C，Lai L L，et al.A Fuzzy Dissolved Gas Analysis Meth⁃od for the Diagnosis of Multiple Incipient Faults in a Transformer［J］.IEEE Transactions on Power Systems，2000，15（2）：593-598.

［19］Wang M H.A Novel Extension Method for Transformer Fault Di⁃agnosis［J］.IEEE Transactions on Power Delivery，2003，18（1）：164-169.

［20］Su Q，Mi C，Lai L L，et al.A Fuzzy Dissolved Gas Analysis Meth⁃od for the Diagnosis of Multiple Incipient Faults in a Transformer［J］.IEEE Transactions on Power Systems，2000，15（2）：593-598.

沈 鑫（1981-），男，汉族，云南人，云南电网公司电力科学研究院，博士研究生，高级工程师，主要研究方向是电能及互感器计量研究，23755803@qq.com；

高文胜（1968-），男，汉族，山东人，博士，副教授，博导，清华大学电机系，主要从事高电压技术及电气设备可靠性研究工作；

刘清蝉（1983-），男，汉族，四川人，云南电网公司电力科学研究院，硕士，从事电能计量检定技术的研究。

曹 敏（1961-），男，汉族，山东人，云南省科技领军人，云南省云岭产业领军人，教授级高级工程师，云南电网公司一级技术专家；

王 昕（1967-），女，汉族，云南人，云南电网公司电力科学研究院，高级工程师，主要研究方向是电能及互感器计量研究；