水下对转桨非空化线谱噪声分析与数值研究

曾赛，杜选民，范威

(上海船舶电子设备研究所 水声对抗技术国防科技重点实验室，上海201108)

0 引言

在航空领域广泛应用的对转螺旋桨具有推进效率高、扭矩平衡等优点，也被应用于水下高速航行体、高速快艇等［1］。近年来，水下或者水上航行体的声隐身指标越来越重要，作为重要噪声源的螺旋桨始终都是被关注的重点。对转桨由于前后桨反向旋转，使得流场的相互作用干扰非常明显，而且梢涡分离特征复杂，对其进行数值噪声预报需要耗费大量计算资源，加之其军事意义显著，使得有关水下对转桨噪声预报分析的文献非常少，大量对转桨噪声预报分析的研究集中在航空领域。

最突出的工作来自于Hanson［2］和Parry［3］，前者基于螺旋面理论和升力面理论，在频域的范围内建立了航空对转桨的噪声预报模型，并且实验验证了模型的准确性;Parry［3］则建立了适于工程计算的航空对转桨噪声计算公式。随着计算机硬件技术的提高，计算气动声学(CAA)与计算流体力学(CFD)的耦合计算方法成为为计算航空螺旋桨噪声的首选，Peters［4］正是基于该方法分析了气动对转桨的噪声谱并阐述了线谱噪声的产生机理。借助航空领域中的成功经验，国内学者针对水下对转桨的噪声预报有过一些尝试。20 世纪90年代，朱锡清等［5］首先讨论了对转桨线谱噪声的理论计算方法，其主要基于升力面理论和声学方法来实现。王顺杰等［6］则对水下对转桨空化线谱频率进行了预报和数值模拟，其基本出发点是认为空泡呈现单极子辐射特征，利用声类比方程推导了远场的声压表达式。杨琼方等［7］则研究了伴流场中对转桨空化初生的判断准则，提出了判断空化初生的4 个充分条件，并且用大规模的数值计算预报了对转桨空化初生时的线谱和宽带谱噪声。

不过，随着螺旋桨设计水平的提高，对转桨设计的趋势是多桨叶、大盘面比、大侧斜等，其最终目的是避免空化和降噪。因此水下对转桨大部分工况下是非空化的。本文主要研究非空化线谱辐射噪声特性，进行数值预报，并对结果进行对比分析。

1 对转桨非空化线谱噪声的理论与分析

1.1 广义声类比方程的变形

由广义声类比方程［8］可知，螺旋桨噪声场可以用单极子、偶极子和四极子来描述。

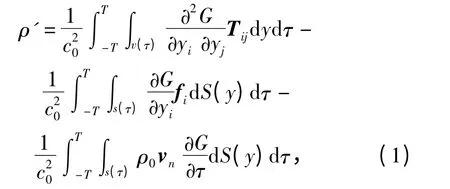
式中:G 表示格林函数;vn、fi均取运动物体表面的外法线方向为正;Tij为ligthhill 应力张量;fi表示流体作用在桨叶表面单位面积上的力的大小;τ= -T 表示在时间平稳过程下，遥远过去对现在的影响;τ =T 表示外伸波条件。右边第1 项表示四极子作用，其本质是lighthill 应力源，在低马赫数时辐射效率很低可以忽略;右边第2 项为偶极子性质的力源;右边第3 项为单极子声源，只有当桨叶出现空化时，才是主要的发声源。本文研究非空化对转桨的非空化线谱噪声问题，偶极子的力源是讨论的重点。

桨叶的实际运动轨迹如图1所示，为了将桨叶表面的力源与远场声压联系起来，建立4 套坐标系，即大地坐标系(x，r，φ)、随动坐标系(x1，r，φ)、叶片固定坐标系(γ，r，ξ)和声源螺旋坐标系(γ0，r0，，ξ0)，图2为声源螺旋坐标系示意图，表示螺旋桨径向距离为r0时叶切面的坐标系，γ0方向与声源点运动方向相反，表示在螺旋方向上离开t=0 时刻螺旋桨母线位置的距离。其中，MCA 为桨叶侧斜距离，FA 为桨叶纵倾距离。

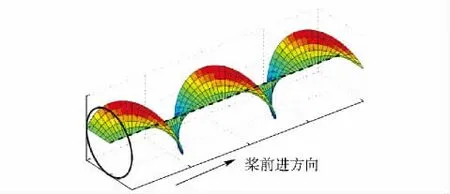
图1 桨叶螺旋面轨迹示意图Fig.1 Schematic diagram of blade＇s helical track

通过坐标系的变换，可将力源点坐标(γo，ro，ξo)用直角坐标(y1，y2，y3)表示，观测点所在的柱坐标(x，r，φ)所对应的直角坐标为(x，rcos φ，rsin φ)，可以计算得到观测点与力源点之间的距离为

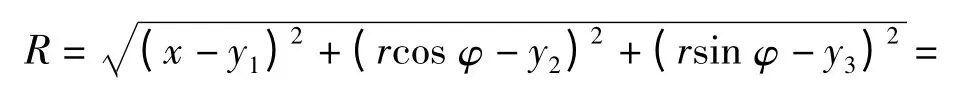
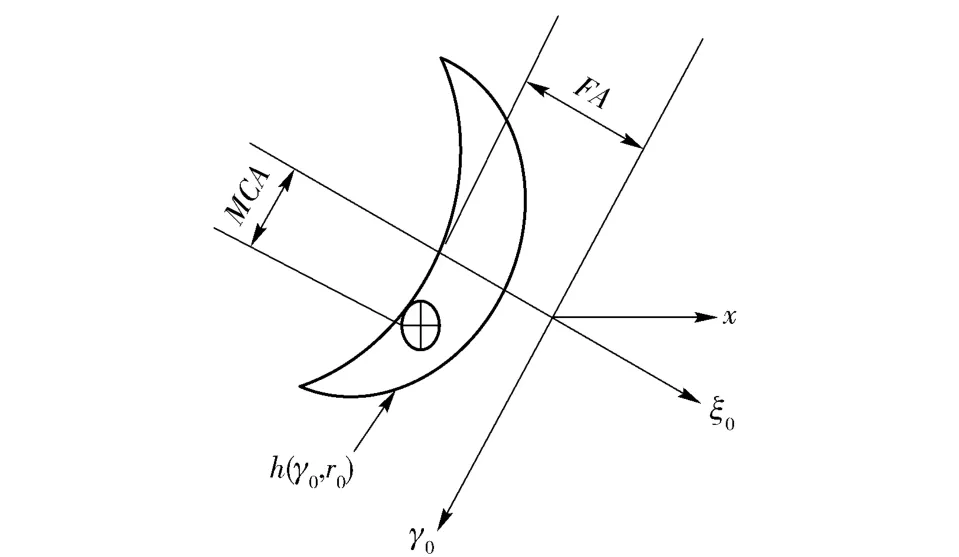
图2 桨叶切面螺旋坐标系示意图Fig.2 Helical coordinate system of blade＇s tangent plane

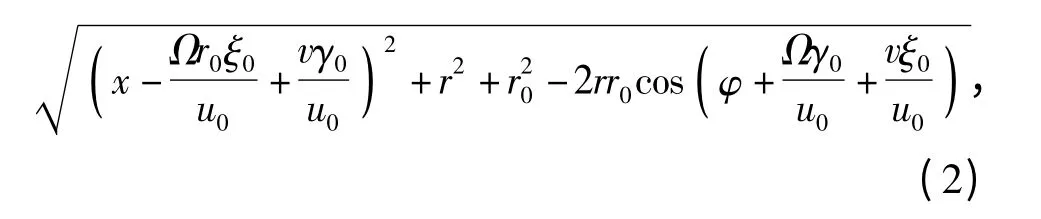
式中:Ω 为桨叶的旋转角速度。

物体运动的法向速度可以表示为:vn= u0·为中间面在运动方向的斜率。由曲面积分可得dγ0dr0，式中:J 为雅可比算子。另外，自由空间中的格林函数为式中:R 表示源点到观察者的距离;c0表示水中声速。由δ 函数的性质，可以将h'表示为对于桨叶上作用力亦可以写成:fj(y，τ)=等式中的ω0表示桨叶上脉动力的圆频率，下标0 表示作用力为定常力。另外，由于声源以u0速度沿着-γ0方向运动，实际的源坐标应该用γ0+u0τ 代替，综合这些考虑，可将(1)式变为

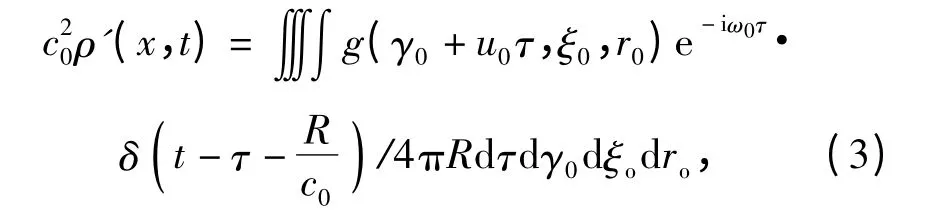
式中:g 为源函数。引入傅里叶变换［9］，

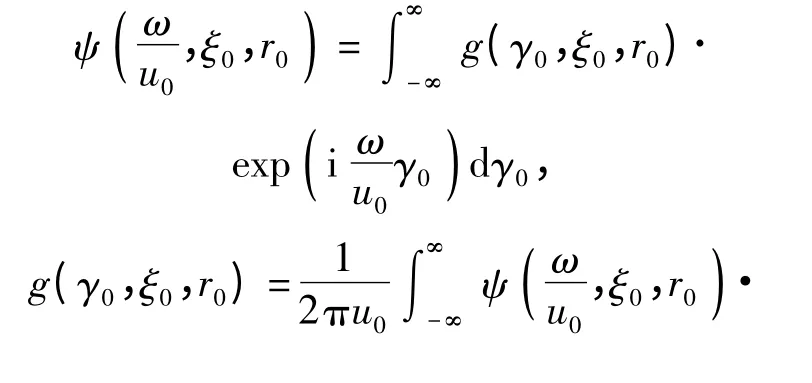
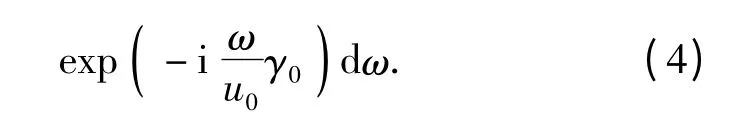
将(4)式代入(3)式对τ 积分可以得到:

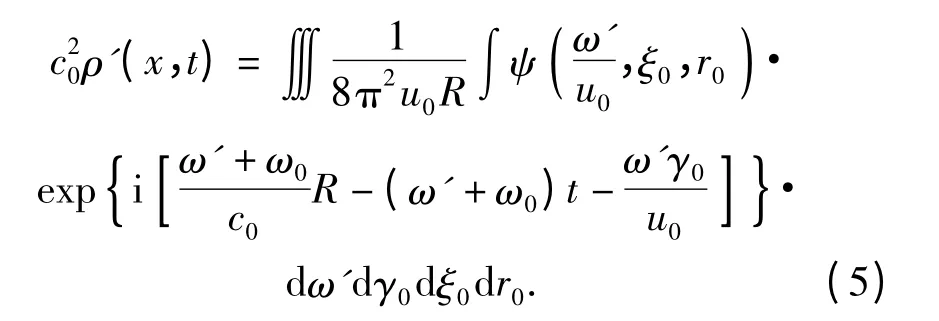
若考虑远场情形，将(2)式作泰勒展开，可以得到:

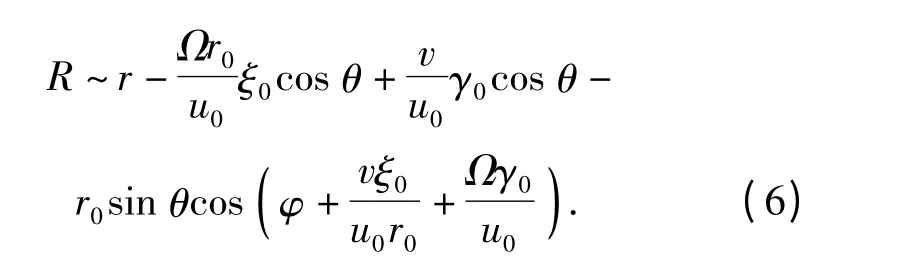
故可以将(5)式中1/R 用1/r 代替，如图3所示。

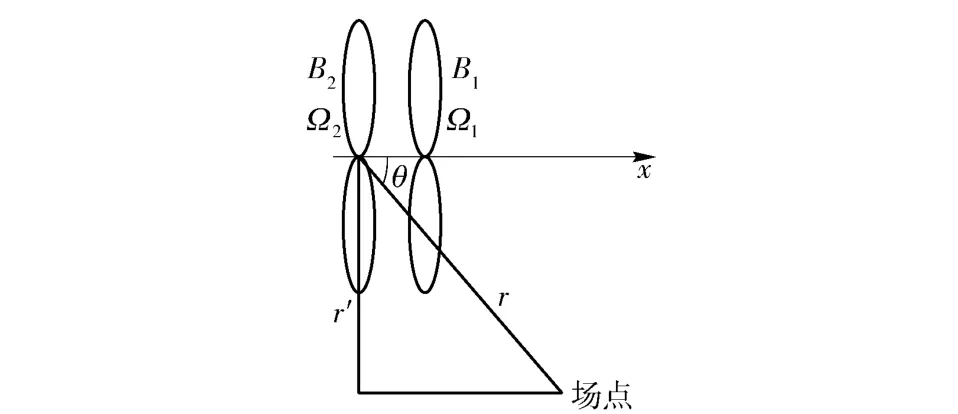
图3 观察点示意图Fig.3 Schematic diagram of viewport in field

1.2 干涉作用以及周向谐波流场作用产生的远场声压

对转桨非空化线谱噪声主要由以下7 种作用产生:非均匀进流与前桨导边相互作用发生、桨叶面附近大尺度涡对桨叶非定常诱导力作用、前桨叶面二次非定常流对后桨作用、后桨抽吸作用形成的非定常压力场与前桨相互作用、前桨梢涡脱落与后桨导边相互作用、前桨随边尾涡脱落与后桨导边相互作用、前桨桨毂尾涡及边界层流与后桨相互作用。这7 种作用又可以分为两类:前后桨相互作用和流场对桨的作用，如图4所示。

干涉作用可以细分为3 个部分:粘性流场、随边势流场和边界层效应。可以用非定常力来衡量这3 个部分作用。设前桨叶片数为B1，旋转角速度为Ω1，后桨叶片数为B2，旋转角速度为Ω2，前桨叶在通过后桨静止叶片时会产生一个干涉流场，表现形式为干涉脉冲，这样在后桨上会产生一个前桨叶片通过频率的单频声源，这样可以将前桨对后桨作用产生的干涉扰动频率表示为

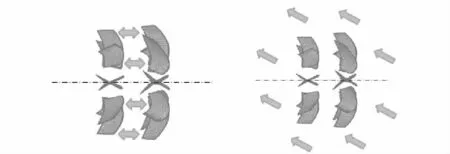
图4 前后桨叶干涉作用(左)与周向谐波流场作用(右)示意图Fig.4 Schematic diagram of interference effect and circumferential harmonic field effect

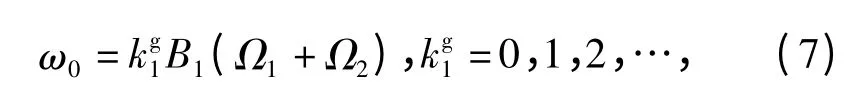
式中:kg1表示前桨对后桨干扰频率的谐波阶数。

取时间因子eiωt，后桨第1 个桨叶上的作用力可以表示为

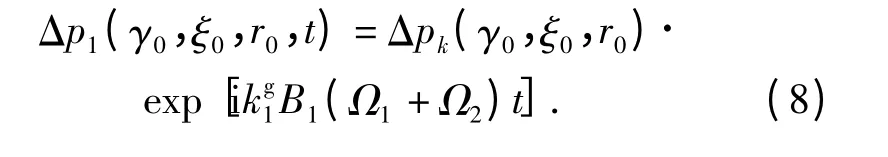
那么第N 个后桨叶上的作用力应该等于第1 个桨叶在位置X、时间T 时的作用力，其中:

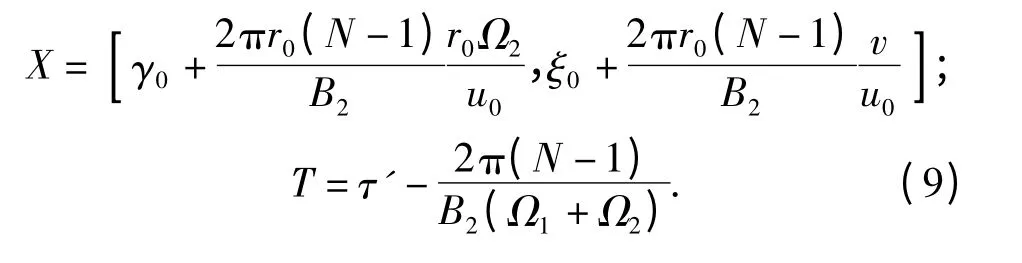
将(9)式代入到(8)式既可得到第N 桨叶的作用力。另一方面，由时间引起的相位变化为

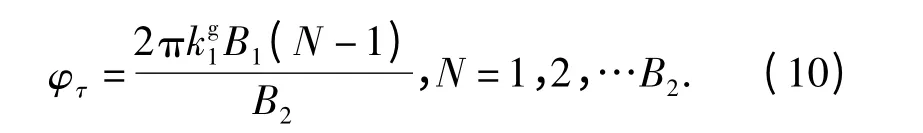
由坐标位置引起的相位变化为

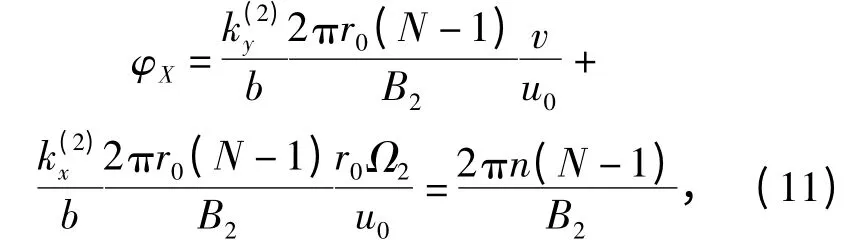
由(10)和式(11)式可知，后桨所有桨叶的相位变化叠加满足

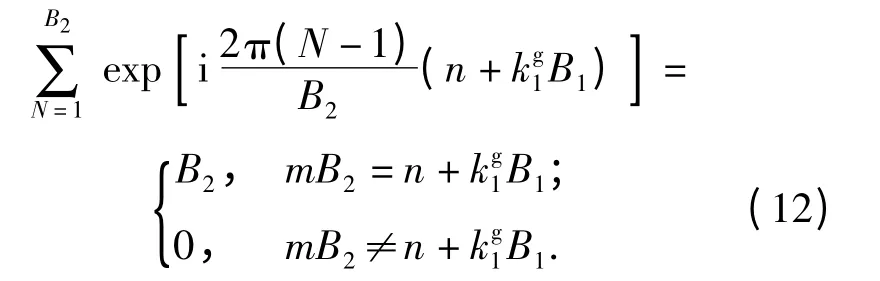
再由特殊函数［10］变形，

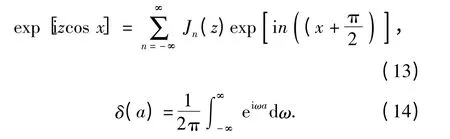
将(6)式～(14)式变形代入到(5)式中，即可以得到后桨在干涉作用下所产生的远场声压:

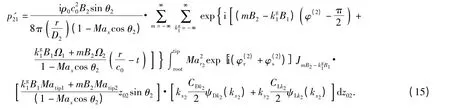
考虑流场对桨叶辐射声压的影响。后桨工作在前桨的非均匀尾流之中，由于后桨的切水作用，会带动周围流场一起旋转使其具有明显的周向调谐性质，设对后桨的调谐分量为W2，对前桨的调谐分量为W1，以后桨为研究对象，每个调谐分量会对后桨叶产生一个激励，会有对应的通过频率，可以将该周向谐波流场的作用频率记为:ω0=k2wW2Ω2(k2w、W2=0，1，2，…)，k2w为后桨调谐谐波分量的阶数。与干涉作用的推导类似，经过一系列的特殊变形可以得到后桨由于流场非均匀流场而产生的远场声压辐射为(15)式和(16)式中积分下、上限分别表示桨叶叶根和叶梢。

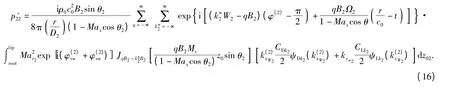
将二者相加既可以得到后桨的远场声压辐射表达式，同理可以得到前桨的远场声压辐射表达式(分析过程不再赘述)。再将前、后桨远场声压辐射公式相叠加即可以得到总的远场声压辐射表达式。上面等式中，干涉作用参数:

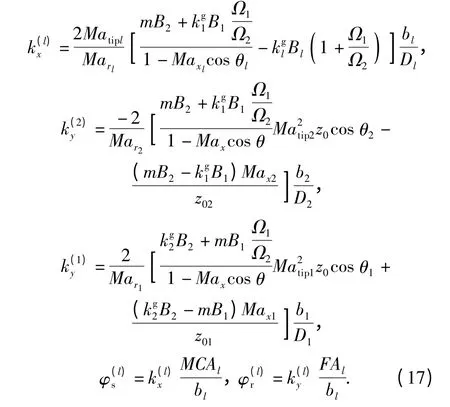
周向调谐流场对桨的作用参数:

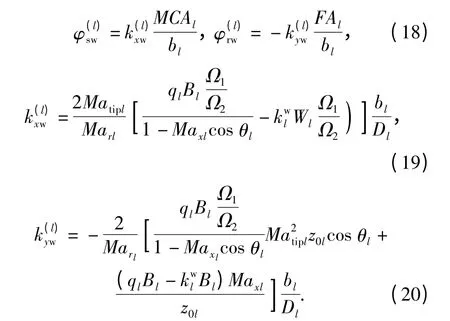
式中:l=1，2，分别表示前、后桨;B1、B2分别表示前、后桨的桨叶数;Dl表示桨的直径，前后桨取各自的直径;rl表示微元源点与测点之间的距离;bl表示前后桨桨叶片对应的弦长;MCA、FA 分别为桨叶侧斜和纵倾的距离;r 为源点到观测点之间的距离;φ(l)表示计算的初始相位角;带下标w 的量表示是流场非均匀性非定常性的影响;Max、Mar和Matip分别表示前进马赫数、微元桨叶切片马赫数和叶片叶梢马赫数;q、m、k1g和k2w表示谐波阶数;θ 表示轴向平面上，测点与轴向的角度，由于轴对称性，这个角度和表示初始角的角度可以将该对转桨整个辐射声场的特性表示出来;CDk、CLk、CDw和CLw分别表示在两种作用下的升阻力系数;ψ 表示形状函数［2］。

本文利用螺旋面理论结合广义声类比方程和特殊函数理论得到对转桨在两种作用下各自的非空化线谱辐射噪声表达式，与文献［5］中利用升力面理论和声学方法得到的表达式有4 个方面的不同。其一，本文同时考虑了升阻力作用，这显然更符合真实情形，而文献［5］只考虑了非定常升力作用。其二，本文变形得到的贝塞尔函数宗量与文献［5］不同，本文中，干涉作用下贝塞尔函数的宗量中所体现的干扰频率是加性的，加性频率为kg1B1Matip1+mB2Matip2，这与(7)式的物理意义是相符合的，而文献［5］中干涉作用下贝塞尔函数的宗量所体现的干扰频率是减性的，有差频的物理意义，文献［5］中没有给出物理解释。其三，无量纲的波数不同，无量纲波数Ky反应了在干涉作用下前后桨辐射噪声重要的相位信息，其对辐射指向性也有重要影响，在气动对转桨噪声领域，Bradley［11］证明了贝塞尔函数阶数的正负(mB2-kg1B1)对于决定声场的源分布有重要作用，文献［5］并没有强调该无量纲波数的作用。其四，本文选用时间因子为eiωt，和文献［5］不同，因而得到的最终辐射表达式也会与文献［5］不同。

1.3 非空化线谱辐射噪声的频率分析

分析对转桨辐射噪声表达式，考虑等式中波的传播因子可以给出不同模式成分波的频率，不失一般性，考虑(15)式中后桨在前桨干涉作用下的传播因子:

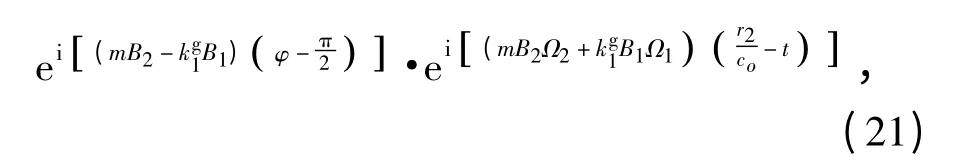
该式表征对转桨的不同模式空间旋转辐射波在φ方向、特征值为(mB2- kg1B1)时，其旋转角速度为(mB2Ω2+kg1B1Ω1). 等式中的时间项是与特征非空化线谱对应的频率。可以看出4 类非空化线谱噪声频率，分别为轴频APF、前桨叶频BPF1及其谐波、后桨叶频BPF2及其谐波、干涉作用频率pBPF1+qBPF2.线谱频率可以看成这4 类非空化线谱频率的组合，即f=sAPF+pBPF1+hBPF2.

1.4 辐射噪声声压方向性讨论

通过辐射声压表达式可以看出，对转桨辐射声压幅值以及方向性均是由贝塞尔函数决定的。讨论(15)式中后桨在干涉作用影响下辐射声压的方向性。定义声压方向函数

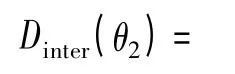
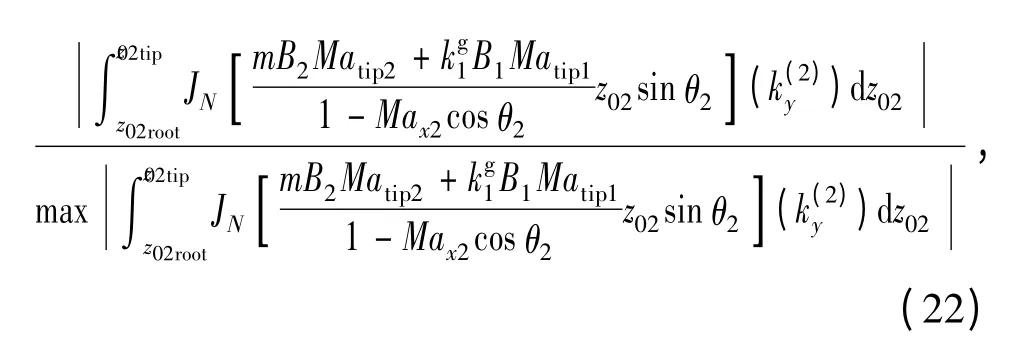
式中:N=mB2-k1gB1，表示贝塞尔函数的阶数，这里定义为辐射模态，(m，k1g)表示非空化线谱的噪声谐波数。将0 阶和前6 阶辐射模态的无量纲声压方向性曲线给出，如图5所示。

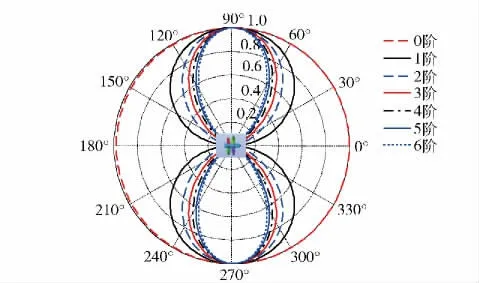
图5 不同模态声压方向性示意图Fig.5 Schematic diagram of sound pressure directivity at different modes

从图5可以看出，除0 阶辐射模态无方向性，前6 阶辐射模态声压方向均表现为“8”字形，呈现偶极子特性，随着阶数的增加，“8”字形越来越尖锐。

1.5 非空化线谱的强弱分析

任意谐波处的声压幅值大小均是由贝塞尔函数决定的，根据贝塞尔函数的性质，对于第1 类贝塞尔函数Jn(x)，其阶数与宗量的差别越大，贝塞尔函数的幅值越小，即当n≪x 时，贝塞尔函数值趋于0. 根据贝塞尔函数的渐进公式:

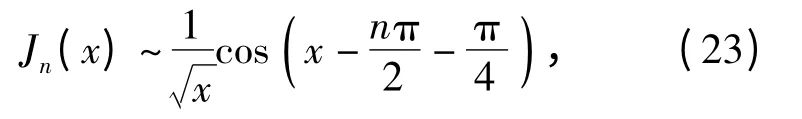
可见，贝塞尔函数在理论上是有无穷多个零点。当干涉作用的贝塞尔函数和周向谐波流场作用的贝塞尔函数同时取0 时，一定没有强线谱出现，可能出现很弱的线谱以至于混淆在连续谱之中。当二者同时取峰值时，一定有强线谱出现。其他的情形都介于二者之间，比如在强线谱附近会出现幅值较弱的一些线谱，但这些线谱又比连续谱强的多，可以认为是较强线谱。这可以作为对转桨非空化强弱线谱出现的条件。

2 对转桨数值模拟以及分析

2.1 数值模型以及网格划分

分别采用Reliable k-ε 湍流模型和RNG k-ε 湍流模型［12］来计算模型桨的水动力性能，并与实验值［13］进行比较，从而得出模拟流场更精确的湍流模型，然后与滑移网格模型相结合，利用FW-H 方程计算目标桨在流场中的声场。本文所用的对转桨基本几何参数如表1所示，模型如图6所示。

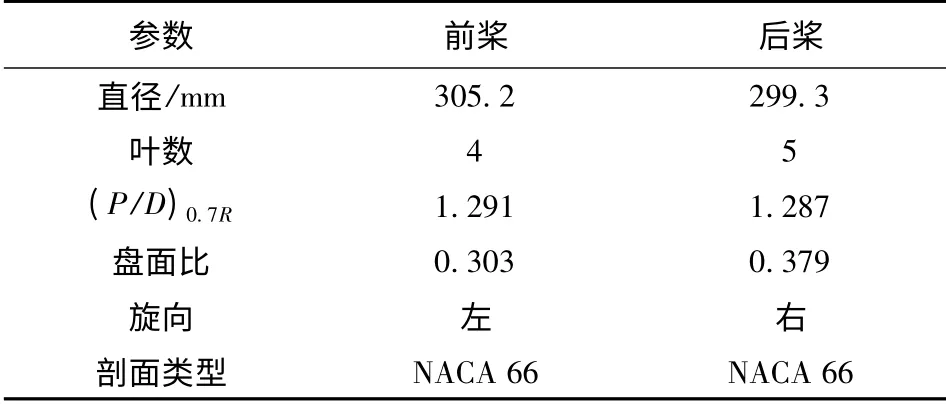
表1 对转桨的几何参数Tab.1 The geometry parameters of CR propeller

图6 对转桨示意图Fig.6 Schematic diagram of counter-rotation propeller

将对转桨置于与其同轴的圆柱体流场之中，上游进流面取为6D，下流面取为10D，径向半径取为5D，D 为前桨直径。螺旋桨在旋转时会带动周围的流体一起旋转，因此在对转桨周围取一个与其同轴的圆柱体作为旋转区域，径向半径取1.3D. 网格划分采用结构-非结构网格。非结构网格1 471 892 个，结构网格2 064 998 个。

2.2 边界条件的设置

整个计算域可以分为入口、出口、静止区域、旋转区域、静止圆柱面、旋转圆柱面和螺旋桨。边界条件分别设置为速度入口、压力出口、静止区域、前桨旋转区域、后桨旋转区域、动静区域交界面、静止圆柱面无滑移墙边界、对转桨叶面设置为运动墙边界和旋转边界，动静域用滑移网格连接。流场的变化通过改变对转桨的进速系数来确定。

2.3 敞水性能验证

进速系数分别选取0.3、0.5、0.7、0.9、1.1，对转桨前后桨转速设为1 072 r/min，转向相反。对转桨的进速系数、推力系数kt以及扭矩系数kq按照文献［14］处理，得到对转桨的敞水性能曲线与试验结果［13］的比较，如图7所示。利用RNG k-ε 模型计算的推力系数与试验值相对误差为3.4%、3.7%、2.2%、1.0%、3.1%，扭矩系数与试验值相对误差为0.07%、1.5%、0.3%、3.9%、7.5%. 利用Realizable k-ε 模型计算的推力系数与试验值相对误差为9.1%、6.3%、1.1%、2.8%、4.6%，扭矩系数与试验值相对误差为0.9%、2.0%、3.0%、4.7%、8.3%.可见RNG k-ε 模型要优于Realizable k-ε，下面用RNG k-ε 模型结合FW-H 方程数值计算对转桨在均匀进流条件下非空化线谱噪声。

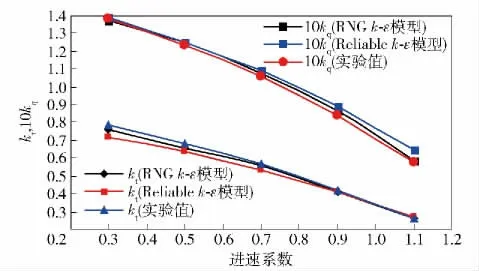
图7 对转桨敞水性能曲线Fig.7 The open water performance curves of CR propeller

2.4 对转桨数值非空化离散线谱模拟及分析

按照RNG k-ε 模型、滑移网格模型与FW-H 方程相结合的方法来预报目标对转桨的非空化离散噪声。首先计算稳态条件下对转桨所在流场，计算收敛后保存计算结果并将其作为非定常流动初始值计算非稳态条件下的对转桨流场［6］，当监视的无量纲系数稳定后进入声学模块的计算。如图8中前、后桨升力系数保持动态稳定，图9表示半个计算周期内前、后桨推力系数ktf、kta均保持动态稳定，表明能够进行声学计算。由于螺旋桨噪声频谱通常在0 ～10 kHz，故设置计算时间步长为5 ×10-5s，计算时长大于0.5 s，所得频率分辨率小于2 Hz，满足分析要求。待计算存储足够多时间步长上测点的脉动声压值后，进入声场分析。按照文献［15］的结论，对转桨线谱大多集中在前13 阶叶频范围内，按照本文设计的对转桨转速估算，目标桨线谱会在0 ～2 kHz 的范围内。

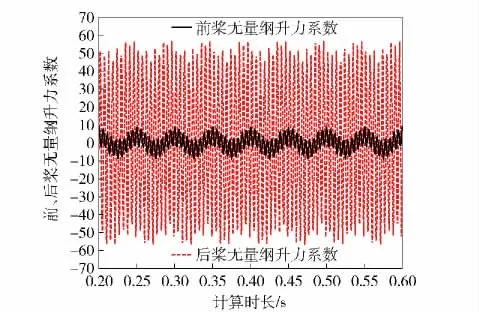
图8 计算无量纲升力系数变化曲线Fig.8 The calculated lift coefficient curves of CR propeller

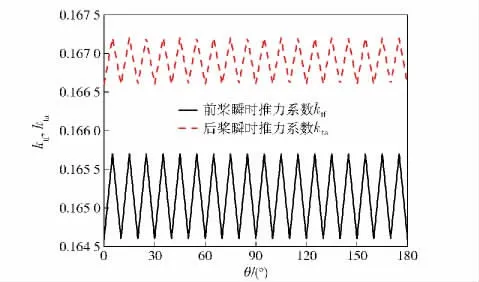
图9 半个周期内前、后桨推力系数变化Fig.9 The thrust coefficient curves of front and rear propellers in half period

图10 为测点布置示意图，其中测点P1 ～P35距桨轴中心为6R1，R1为前桨半径。测点沿着圆周等距分布且沿着轴向面布置，P37、P39 测点分别布置在前、后桨的径向方向上，P38 布置在前、后桨中间平面上。分别观察5 个典型测点的声压频谱特性，如图10 所示，f0、f1、f2分别为轴频和前、后桨叶频。在轴向测点P1 的声压频谱上，线谱主要出现在叶频上，峰值线谱出现在组合叶频5f1+4f2上，此组合对应于贝塞尔函数的阶数为0 阶，这说明前、后桨之间的干涉作用在轴向表现得较为明显;在径向测点P38 的声压频谱上，线谱几乎都出现在叶频及其谐波上，考虑到叶频与轴频的倍数关系，可以认为桨叶径向处的线谱都出现在轴频及其谐波处;在轴向和径向之间的测点的声压频谱上，如测点P7、P14，声压谱峰值几乎都出现在前、后桨相互干扰的频率上，这说明在非径向和非轴向处，前、后桨之间的干涉作用非常显著。如图11 所示，在5f1+4f2频率对应的功率谱密度最大，与声压频谱相吻合。如图12 所示，在1 阶叶频以及f1+ f2处对应的功率谱密度最大，随着谐波阶数增加、功率谱密度逐渐减小。如图13 所示，在f2和f1+f2频率对应的功率谱密度最大。结合声压谱可以看出，在0 ～2 000 Hz 的范围内存在多条与前、后桨叶频相关的线谱。如图14 所示为各测点所得声压级连接曲线，可以看出与1.4 节所得的声压方向性大致吻合，总声压级呈“8”形状。

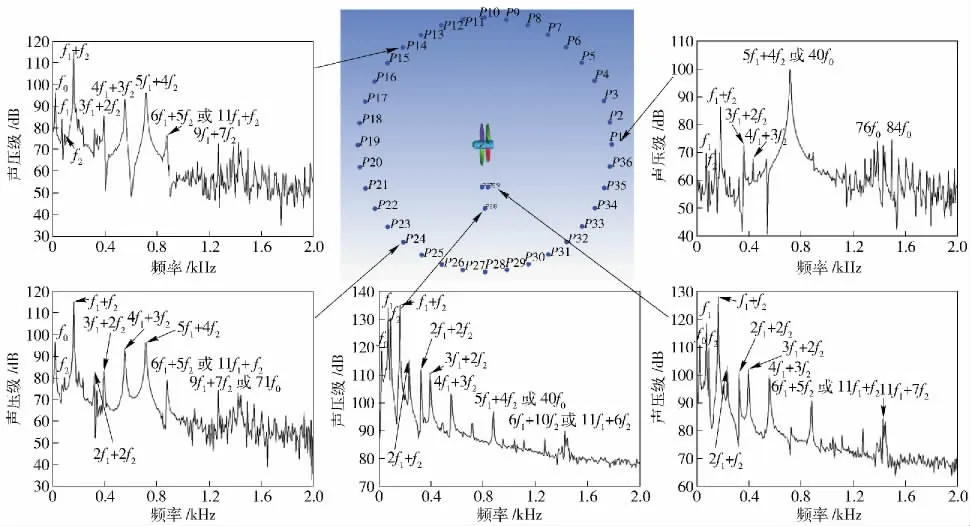
图10 典型测点的声压谱示意图Fig.10 Schematic diagram of typical sound pressure spectra at measuring point

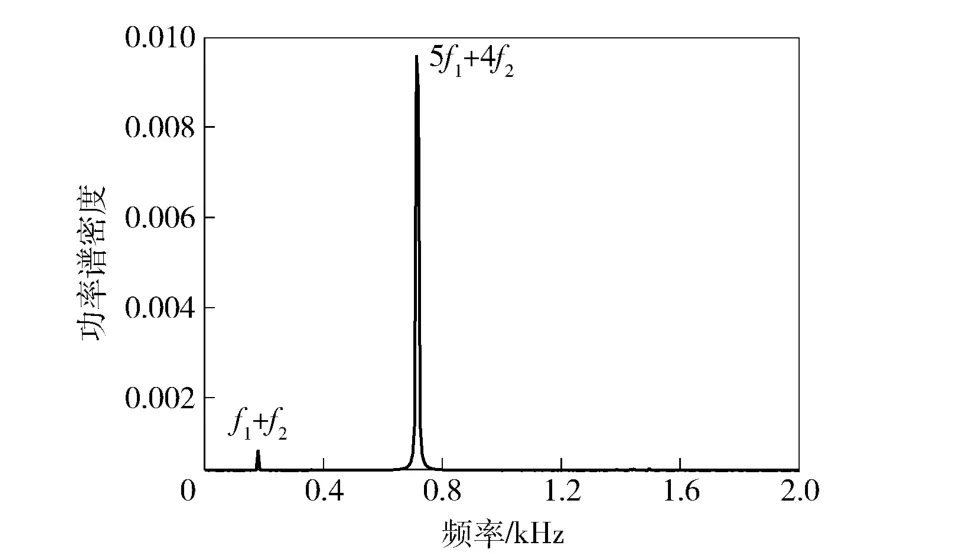
图11 P1 点的功率谱Fig.11 Power spectrum at P1

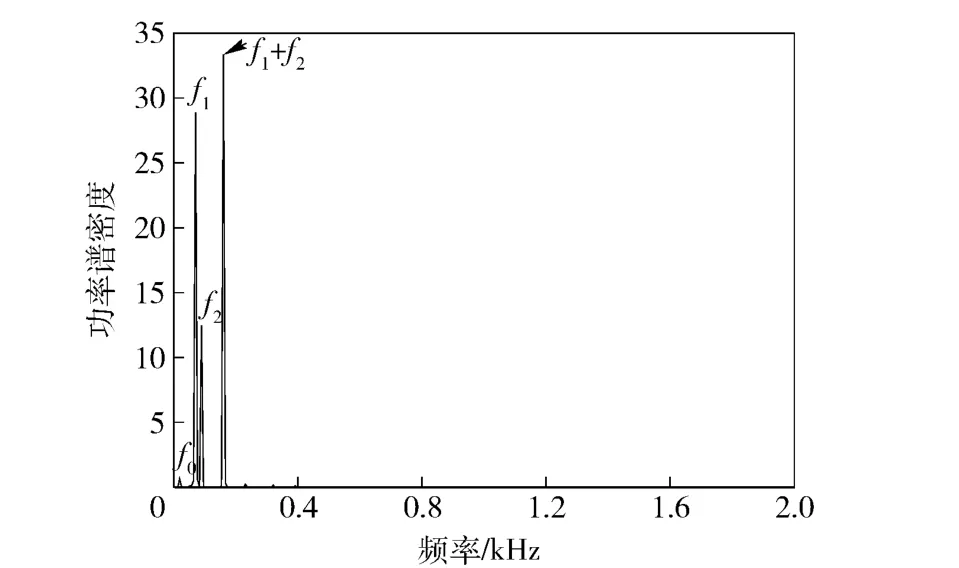
图12 P38 点的功率谱Fig.12 Power spectrum at P38

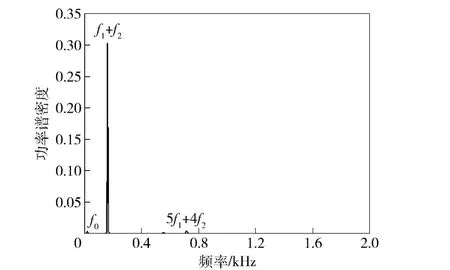
图13 P39 点的功率谱Fig.13 Power spectrum at P39

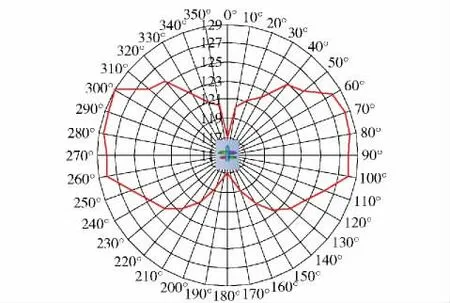
图14 测点声压级变化曲线Fig.14 SPL curve at measuring point

3 结论

通过分析对转桨非空化噪声的特性，以期为水下目标识别和分类提供判断依据。通过理论和数值计算分析，得到如下结论:

1)水下对转桨非空化线谱噪声由7 种作用共同作用形成。从机制上来看可以分为两类，即前、后桨干涉作用和非均匀流场作用。这些因素共同作用使得对转桨噪声线谱非常丰富。

2)水下对转桨非空化线谱噪声预报频率为f=sAPF+pBPF1+hBPF2，系数s、p、h 为整数。

3)水下对转桨非空化噪声辐射声压具有方向性。径向方向的总声压要强于轴向方向。

4)计算对转桨水动力性能方面，RANS 方法能够取得符合工程应用的精度，且RNG k-ε 模型要优于Reliable k-ε 模型。

5)通过uRANS 方法结合FW-H 方程的混合数值算法能够合理地模拟对转桨非空化噪声问题，模拟的非空化线谱与理论吻合度较好。

References)

［1］常煜，洪方文，张志荣，等.对转桨水动力性能的数值分析［C］∥2008年船舶水动力学学术会议暨中国船舶学术界进入ITTC30 周年纪念会论文集.杭州:中国造船工程学会，2008.CHANG Yu，HONG Fang-wen，ZHANG Zhi-rong，et al. Numerical study of contra-rotating propellers hydrodynamic performance［C］∥The Ship Hydrodynamics Conference and the Shipbuilding Academic of China Step into the ITTC30 Anniversary Conference.Hangzhou:China Shipbuliding Engineering Society，2008. (in Chinese)

［2］Hanson D B. Noise of counter-rotation propellers［J］. Journal of Aircraft，1985，22(7):609 -617.

［3］Parry A B. Theoretical prediction of counter-rotation propeller noise［D］. UK:University of Leeds，1988.

［4］Peters A. Assessment of propfan propulsion systems for reduced environmental impact［D］. US:Massachusetts Institute of Technology，2010.

［5］朱锡清，吴武生. 水下高速航行体对转螺旋桨线谱噪声预报研究［J］.声学学报，1998，23(2):123 -134.ZHU Xi-qing，WU Wu-sheng. Prediction of line-spectrum noise induced by high speed vehicle counter-rotation propellers in water［J］. Acta Acustica，1998，23(2):123 -134.(in Chinese)

［6］王顺杰，程玉胜，高鑫.水下对转螺旋桨空化线谱频率预报与数值模拟［J］.兵工学报，2013，34(3):311 -319.WANG Shun-jie，CHENG Yu-sheng，GAO Xin. Prediction and numerical simulation of cavitation noise line-spectrum frequency induced by underwater counter-rotation propeller［J］. Acta Armamentarii，2013，34(3):311 -319.(in Chinese)

［7］杨琼方，王永生，张志宏，等.伴流场中对转桨空化初生的判断与辐射噪声预报和校验［J］. 声学学报，2014，39(5):590 -606.YANG Qiong-fang，WANG Yong-sheng，ZHANG Zhi-hong，et al.Numerical prediction of cavitation inception radiated noise of contra-rotating propeller with non-uniform inflow［J］. Acta Acustica，2014，39(5):590 -606.(in Chinese)

［8］孙小峰，周盛.气动声学［M］.北京:国防工业出版社，1993.SUN Xiao-feng，ZHOU Sheng. Aeroacoustic［M］. Beijing:National Defense Industry Press，1993. (in Chinese)

［9］乔渭阳.航空发动机气动声学［M］. 北京:北京航空航天大学出版社，2010.QIAO Wei-yang. The aeroacoustic of aircraft engine［M］. Beijing:Beijing University of Aeronautics and Astronautics Press，2010. (in Chinese)

［10］梁昆淼.数学物理方法［M］.北京:高等教育出版社，2011.LIANG Kun-miao. The methods of mathematical physics［M］.Beijing:Higher Education Press，2011. (in Chinese)

［11］Bradley A J. A study of the rotor/rotor interaction tones from a contra-rotating propeller driven aircraft［R］. Reston，VA:AIAA，1986:1886 -1894.

［12］王福军.计算流体动力学分析-CFD 软件原理与应用［M］.北京:清华大学出版社，2010.WANG Fu-jun. Analysis of computational fluid dynamics-CFD software principle and application［M］. Beijing:Tsinghua University Press，2010. (in Chinese)

［13］Miller M L. Experimental determination of unsteady forces on counter-rotating propellers in uniform flow，SPD-659-01［R］.Maryland:David Naval Ship Research and Development Center，1976.

［14］张涛，陈彦勇，杨晨俊.RANS 方法预报对转桨定常敞水性能研究［J］.船舶工程，2011，33(5):23 -26.ZHANG Tao，CHEN Yan-yong，YANG Chen-jun. Study on the prediction of contra-rotating propellers open-water steady performance using RANS formula［J］. Ship Engineering，2011，33(5):23 -26.(in Chinese)

［15］马徐琨.浅析水下高速航行体对转螺旋桨辐射噪声线谱建模［J］.声学学报，2002，27(6):503 -506.MA Xu-kun. Preliminary modeling of line spectrum for radiated noise induced by high speed counter rotation of underwater vehicle propellers［J］. Acta Acustica，2002，27(6):503 -506.(in Chinese)