基于自抗扰的自主水下航行器地形跟踪控制

万磊，张英浩，孙玉山，李岳明

(哈尔滨工程大学 水下机器人技术重点实验室，黑龙江哈尔滨150001)

0 引言

自主水下航行器(AUV)要完成海底管线跟踪和海床地质调查等任务，前提是需要具有精确的地形跟踪能力。所谓地形跟踪是指，AUV 以合适的方式下潜到作业水深之后，与水底保持一定高度，并按照一定的航线航行［1］。随着AUV 工作任务的日益复杂化，人们对于AUV 在未知环境中的控制精度，以及抵抗外界干扰的要求也在不断提高。

当前AUV 的地形跟踪难点在于:1)海底崎岖不平，地形变化剧烈，导致跟踪困难;2)水下机器人垂向运动的机动能力有限;3)声学传感器对高度测量结果噪声大［1］。针对以上难点，国内外的相关学者进行了大量的研究，并取得了一定的成果［1-6］。Smith 等［2］将模糊控制方法引入运动控制器的设计，从而提高AUV 在跟踪任务时的鲁棒性。Jose 等［3］对MARES AUV 上安装的传感器数据进行适当处理，并结合设计的控制策略生成AUV 的跟踪控制指令。段海庆等［4］则利用神经网络控制方法，来降低AUV 在跟踪过程中不确定扰动对精度的影响。李岳明等［1］利用Takagi-Sugeno 推理方法对高度计和DVL 两种传感器的高度信息进行信息融合，从而提高高度信息的感知能力，以保障AUV 可准确进行地形跟踪。Carlos 等［5］利用水声设备测量地形时的声学特征，来对AUV 进行指令下达，并进行了相关仿真测试。

本文将重点放在AUV 的运动控制上，主要设计了具有保护功能的控制策略以及能够抵抗环境干扰的控制器，并与PID 控制方法进行对比实验，完成地形跟踪所需的全过程三维运动仿真。

1 控制对象及运动建模

1.1 控制对象及坐标系

本文的控制对象是由哈尔滨工程大学水下机器人技术重点实验室设计的某型AUV，其主体大致成细长回转体，艇体艏部和艉部各装有垂向推力器一套，艉部装有舵、翼和主推等各一套。为研究问题和后文叙述方便，分别建立大地坐标系Eξηζ 和艇体坐标系Oxyz，如图1所示。Eξηζ 是惯性坐标系，而Oxyz 属于非惯性坐标系，并且Oxyz 的原点O 与AUV 的重心G 重合。

图1 AUV 主体及所建立坐标系Fig.1 AUV and coordinates

为清楚表述纵倾角θ，图1显示的是坐标轴Eη和坐标轴Oy 平行的情况，并标注出θ 的正方向。

1.2 动力学及运动学方程

由文献［7］可知，当AUV 在垂直面内运动时，其动力学及运动学方程可分别表示为(1)式和(2)式。

式中:M 为惯性质量矩阵，鉴于所控制AUV 外形在垂向对称性，因而可表示为

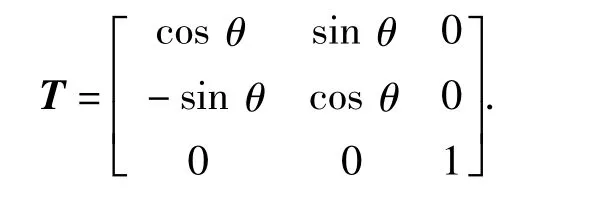
2 垂直面地形跟踪策略

2.1 “高度－深度”转化

AUV 在进行地形跟踪控制时，一般在水平面会沿指定路径运动，而在垂直面会以与水底呈一定高度的方式运动。其会通过“高度计”和“深度计”等传感器分别获得当前位置距跟踪地形的高度信息和当前深度信息，以此为地形跟踪的依据。

图2所示为“高度”与“深度”之间的信息关系。假使AUV 处于位置P，如需对指定地形进行跟踪，当前距跟踪地形高度为hP，所在位置深度为ζP，若期望跟踪高度为h0，则“高度-深度”之间的转化关系，可表述为(3)式。

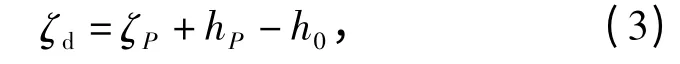
式中:ζd为期望深度，也就是AUV 的期望控制深度。

图2 “高度-深度”关系图Fig.2 Relation graph of altitude and depth

2.2 “深度－纵倾”转化

本文所研究的AUV 虽然布置有垂向推进器，但是当AUV 纵向速度或外界流较大时，垂向推进器的效率会大幅减少。因而，在进行AUV 的深度控制时，需考虑“深度”与“纵倾”之间的转化关系。

因而，设计“深度-纵倾”的转化关系，可表述为(4)式。

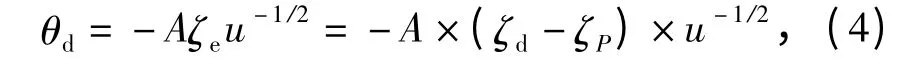
式中:θd为期望纵倾角;ζe为期望深度ζd与当前深度ζP之差;A 为可调参数，与AUV 的运动性能呈正相关，且A ＞0.

这种方式可能会出现解算出的θd过大的情况，因而，为避免AUV 运动过程中危险姿态的出现，保证其安全，进而建立“期望纵倾角保护”机制，即为(4)式解算出的期望纵倾角θd设定“安全阈值”。当解算出的θd超过设定阈值，则按安全阈值进行控制输入。因而，整个垂直面内的地形跟踪控制策略，可由图3表示。

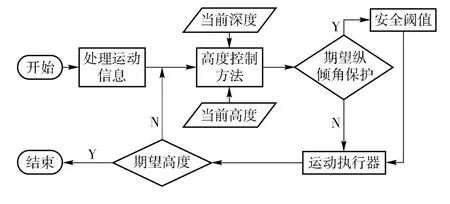
图3 AUV 垂直面地形跟踪策略Fig.3 AUV bottom-following strategy on vertical plane

3 AUV 跟踪控制器的建立

3.1 自抗扰控制器

自抗扰控制(ADRC)是由中国科学院系统科学院研究所韩京清研究员提出的一种控制方法［8］，其继承了传统PID“基于误差，消除误差”的思想。主要由跟踪微分控制器(TD)、扩张状态观测器(ESO)、误差的非线性反馈(NLSEF)以及扰动估计补偿等部分组成。若以2 阶ADRC 控制器建立AUV 水平舵控制器，则其信息流框架如图4所示。

图4 水平舵ADRC 控制器信息流框架Fig.4 Information frame of wing’s controller based on ADRC

图4中的θd和θ 分别为期望纵倾角和AUV 当前纵倾角，其他变量为ADRC 控制器计算所需的中间变量。本文根据控制需求，将图4中各部分算法设计如下:

TD:

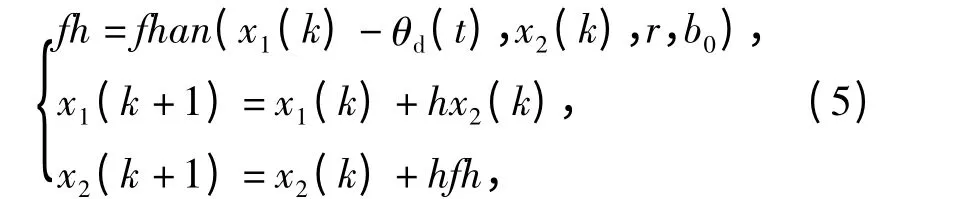
式中:r 为快速因子;b0为滤波因子。

ESO:

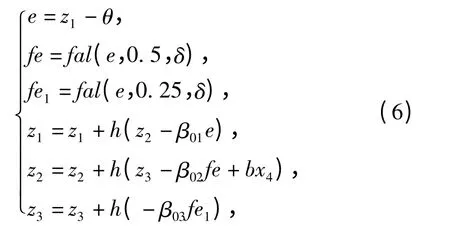
式中:β01、β02、β03为增益系数;δ 为可调参数。

NLSEF:

式中:e1为纵倾角偏差;e2为纵倾角偏差变化率。

扰动估计补偿:

式中:b 为可调参数。

(5)式～(7)式中:h 为积分步长;fhan(·)和fal(·)的定义如文献［9］中所述。

通过ADRC，可以将纵倾角的控制问题，转化为纵倾角偏差e1和纵倾角偏差变化率e2的镇定问题。主推ADRC 控制器和垂直舵ADRC 控制器的设计与水平舵的类似。

3.2 地形跟踪控制器

AUV 在进行完整的地形跟踪的任务时，一般会按照“下潜-巡航-跟踪”的模式进行。“下潜”的过程又可分为“自主下潜”和“非自主下潜”。所谓“自主下潜”是指AUV 依靠自身的运动执行器完成下潜任务，而“非自主下潜”是指AUV 依靠“自身重力与自身浮力”之间的差值进行下潜，如抛载块、油囊等［10］。“自主下潜”与“非自主下潜”各有优劣，“自主下潜”对于未知环境的突然变化具有良好的应对能力，而“非自主下潜”则在能源节省方面具有明显优势。本文主要研究通过“自主下潜”的方式完成“下潜”过程。

对于浅水情况，AUV 可“直接”潜到指定深度。对于深水情况，AUV 一般采用“螺旋”下潜的方式。图5显示，在无外界干扰情况下，航速4 kn 时，利用(4)式中的“深度-纵倾”转化关系以及图4中的水平舵ADRC 控制器完成的浅水区多深度定深运动。在此过程中，分别定深3 m、6 m 和12 m. 可见ADRC的控制参数一旦选定，就可具有较大的适用范围，并且控制效果良好。

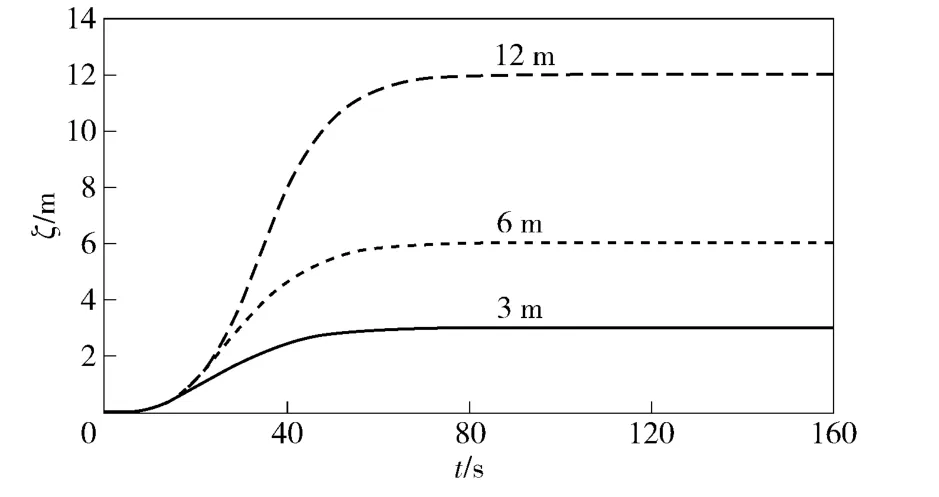
图5 定深运动结果Fig.5 Results of depth control

在到达指定深度之后，AUV 会进入“巡航”过程，主要是为了对周围环境进行信息采集，并确认跟踪区域。“巡航”结束之后，AUV 会根据任务需求，开始按照指定路径进入“跟踪”过程。AUV 的完整地形跟踪控制器信息流框架可表示为图6.

4 仿真实验与结果分析

4.1 实验设计

本文尝试通过进行AUV 完整的地形跟踪三维仿真，来测试所设计地形跟踪控制器的有效性。为显示ADRC 的控制效果，将其与在工程上广泛应用的PID 控制器进行对比，相关设计如下。

干扰的设计。添加Eξ 和Eζ 方向的随机干扰，用于模拟外界环境干扰以及AUV 自身的信号传输干扰;添加Eη 方向的恒值干扰，用于模拟流的作用效果;添加ζE 方向的瞬时干扰，用于模拟水底暗涌或喷流所导致的环境突然变化。

图6 AUV 地形跟踪控制器信息流框架Fig.6 Information flow frame of AUV＇s bottom-following control

运动航迹的设计。结合参考文献［11 -12］，“下潜”过程，在Eξη 面内，设计航迹为以(0，0)为圆心，半径为50 m 的圆;当到进入“巡航”过程之后，继续以先前的圆轨迹运行一段时间;当到进入“跟踪”过程之后，以Eξη 面内过(0，0)，艏向角φ=90°的直线进行运动。

AUV 艇长4.5 m，质量700 kg，转动惯量Iy=1 430 kg·m2，部分无因次化水动力系数如表1所示。

表1 AUV 部分无因次化水动力系数Tab.1 Part of AUV’s dimensionless coefficients

运动初始AUV 已通过垂推下潜到ζ=5 m 的位置，目的是为避免环境表面风浪的影响保证舵效，此时AUV 的艏向角φ=0°，纵倾角θ=0°，悬浮位置坐标为(0，0，5 m). 设计AUV 以航速2 kn，地形跟踪期望高度h0=5 m 运动，“下潜”、“巡航”和“跟踪”的切换深度位于ζ=100 m 位置。

4.2 实验分析

调整好相关控制器参数后，假使ADRC 和PID两种控制器跟踪的地形相同，则得到如图7～图10所示结果。

图7中的1、2 和3 过程，分别指“下潜”、“巡航”和“跟踪”。可知，基于ADRC 的地形跟踪控制器和基于传统PID 的地形跟踪控制器均能按指定航迹完成地形跟踪任务。其中，“下潜”过程，对应t 为0 ～400 s;“巡航”过程，对应t 为400 ～600 s;“跟踪”过程，对应t 为600 ～1 000 s;瞬时干扰，出现于t 为800 s 时。

图7 地形跟踪全过程三维航迹Fig.7 Three-dimensional track of bottom-following control

图8显示，当分别以ADRC 和PID 控制纵向速度时，ADRC 控制器相比于PID 控制在进入期望值之前不会出现超调，并且在遭遇瞬时干扰后，ADRC控制器的波动值要远小于PID 控制器的波动值。

图8 地形跟踪全过程速度变化曲线Fig.8 Curves of velocity in bottom-following control

图9显示，当AUV 由“巡航”转为“跟踪”时，相比PID 控制器，ADRC 可以实现平滑过渡，几乎没有超调。并且在进入“跟踪”过程后，面对出现的瞬时干扰，也有较好地抑制作用，从而保证维持在水底上方5 m 处运动。

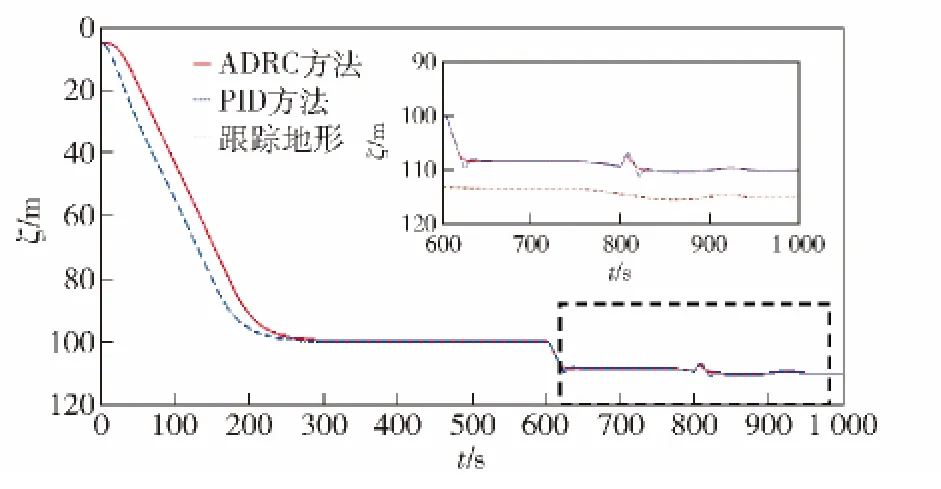
图9 地形跟踪全过程深度变化曲线及虚线框放大曲线Fig.9 Curve of depth in bottom-following control and enlarged detail of the dashed frame

图10 显示，AUV 的翼角有些段数据近似于0，这是由于建模过程中未考虑扶正力矩引起的，但这并不影响对ADRC 和PID 控制指令输出的性能对比。在t 为0 ～100 s 和t 为600 ～900 s 过程中，PID 控制的翼为达到目标状态会不断修改运动执行器指令，相比而言，ADRC 控制下的翼运动则稳定得多。

图10 地形跟踪全过程翼角变化曲线Fig.10 Curves of wing’s degree in bottom-following control

图11 显示，AUV 处于“下潜”过程时，有一段纵倾角维持在-30°的过程，这是由于按照2.2 节中的地形跟踪策略，将“安全阈值”设定为30°的原因。在AUV 进入“跟踪”过程之后，ADRC 控制器的纵倾变化一直处于一种缓变过程，而PID 控制器的纵倾变化则处于一种震颤过程，特别是在“巡航”与“跟踪”的切换过程，以及受到瞬时干扰的作用后。PID控制效果的震颤是由于PID 控制器自身性能以及随机干扰的作用引起的，由此显示出ADRC 控制器的优势。纵倾的缓变，将有利于AUV 上传感器的工作。

图11 地形跟踪全过程纵倾角变化曲线Fig.11 Curves of pitch angle in bottom-following control

5 结论

基于自抗扰的自主水下航行器地形跟踪控制方法，结合了自抗扰控制器的优点并且设有保护机制的地形跟踪策略。与传统PID 控制器的对比实验中，显示所设计地形跟踪控制方法的有效性，在“下潜-巡航-跟踪”的整个地形跟踪任务中，能够对干扰具有更优的抑制作用，进而更准确地完成预定地形的跟踪任务。

References)

［1］李岳明，万磊，孙玉山，等. 水下机器人高度信息融合与欠驱动地形跟踪控制［J］. 控制理论与应用，2013，30(1):118 -121.LI Yue-ming，WAN Lei，SUN Yu-shan，et al. Altitude information fusion and bottom-following control for underacutated autonomous underwater vehicle［J］. Control Theory ＆ Appllications，2013，30(1):118 -121. (in Chinese)

［2］Smith S M，White K，Xu M. Fuzzy logic flight and bottom following controllers for the ocean voyager II AUV［C］∥Proceedings of the Joint Conference on Information Sciences. Pinehurst:Duke University/Association for Intelligent Machinery，1994:56 -59.

［3］Jose M，Anibal M. Bottom estimation and following with the MARES AUV［C］∥OCEANS 2012 MTS/IEEE:Harnessing the Power of the Ocean. Virginia:IEEE Computer Society，2012:1 -8.

［4］段海庆，贾鹤鸣，周佳加，等. 基于神经网络的欠驱动水下机器人地形跟踪控制［J］. 东南大学学报:自然科学版，2012，42(1):203 -207.DUAN Hai-qing，JIA He-ming，ZHOU Jia-jia，et al. Bottom following control forUnderactuated AUV based on neural network［J］.Jouranal of Southeast University:Natural Science Edition，2012，42(1):203 -207. (in Chinese)

［5］Carlos S，Rita C，Nuno P，et al. A bottom-following preview controller for autonomous underwater vehicles［J］. IEEE Transactions on Control Systems Technology，2009，17(2):257 -266.

［6］Adhami-Mirhosseini A，Yazdanpanah M J，Aguiar A P. Automatic bottom-following for underwater robotic vehicles［J］. Automatica，2014，50(8):2155 -2162.

［7］施生达.潜艇操纵性［M］. 北京:国防工业出版社，1995:149 -159.SHI Sheng-da. Submarine maneuverablity［M］. BeiJing:National Defense Industry Press，1995:149 -159. (in Chinese)

［8］韩京清. 自抗扰控制器及其应用［J］. 控制与决策，1998，13(1):19 -23.HAN Jing-qing. Auto-disturbances-rejection controller and its applications［J］. Control and Decision，1998，13(1):19 -23. (in Chinese)

［9］韩京清. 自抗扰控制技术——估计补偿不确定因素的控制技术［M］.北京:国防工业出版社，2009:243 -261.HAN Jing-qing. Active disturbance rejection control technique—the technique for estimating and compensating the uncertainties［M］.Beijing:National Defense Industry Press，2009:243 - 261. (in Chinese)

［10］朱继懋. 潜水器设计［M］.上海:上海交通大学出版社，1992:65 -109.ZHU Ji-mao. The design of underwater vehicle［M］. Shanghai:Shanghai Jiao Tong University Press，1992:65 -109. (in Chinese)

［11］Sun Y S，Zhang Y H，Zhang G C，et al. Path tracking control of underactuated AUVs based on ADRC［C］∥Proceeding of 2013 Chinese Intelligent Automation Conference:Intelligent Automation.Yangzhou:Spring Verlag，2013:609 -615.

［12］万磊，张英浩，孙玉山，等. 欠驱动智能水下机器人的自抗扰路径跟踪控制［J］. 上海交通大学学报，2014，48(12):49 -54.WAN Lei，ZHANG Ying-hao，SUN Yu-shan，et al. ADRC pathfollowing control of underactuated AUVs［J］. Journal of Shanghai Jiao Tong University，2014，48(12):49 -54. (in Chinese)