白车身装焊误差区域识别过程中伪相关点的剔除

王灵犀，刘庆坤,布占行

(沈阳理工大学 汽车与交通学院，辽宁 沈阳 110159)

白车身装焊误差区域识别过程中伪相关点的剔除

王灵犀，刘庆坤,布占行

(沈阳理工大学 汽车与交通学院，辽宁 沈阳 110159)

使用聚类分析方法寻找白车身装焊误差区域过程中，有伪相关点混入误差区域内影响区域识别的准确性，为此提出对各初始误差区域各自做相关来剔除伪相关点的方法。实验结果表明：将整车聚类分析结果划分为初始误差区域，并采用相同的相关系数对各区域各自做相关能够有效剔除伪相关点，其余符合相关条件的测点构成的区域更加清晰准确，有利于误差源的诊断。

聚类分析；白车身；伪相关点；相关分析

汽车白车身装焊误差源的识别中往往要寻找误差区域，当误差区域的形态与某种工序状态相似时，则预示误差在此道工序中发生[1]。陈猛等[2]利用相关分析寻找车身覆盖件之间的联动性来确定误差区域，其弊端在于分析之前不能准确确定“母点”。胡敏等[3]利用主成分分析研究相关系数矩阵的特征值和相应的特征向量判断误差源，但只能对车身某一指定分总成进行分析。以相关系数为聚类尺度和聚类样本筛选阈值，用误差点出现的频率划分聚类阶数，采用聚类分析可以全面准确地寻找误差区域[4]。但在实际操作中经常会发现一种现象：所形成的误差区域中有些误差点的相关系数低于阈值，却能通过样本筛选进入该误差区域，干扰对误差区域的判断。本文称这些误差点为“伪相关点”，提出通过各初始误差区域各自做相关剔除这些伪相关点的方法。

1 伪相关点的剔除方法

1)通过聚类分析寻找误差区域：分析时首先设置合适的相关系数作为聚类尺度，对于聚类尺度的选择应视具体情况而定，不同车型的聚类尺度可能不同，也可能相同，但对于同一车型的不同区域相关系数必须相同，一般是从较低的相关系数开始，逐步提高直至出现较合理的区域；然后对整车全部测点进行聚类分析，得出分析结果后，从低到高显示各阶聚类样本中的误差点并观察其分布形态，当某阶聚类测点的形态与某些工序状态相似时，则可据此判断出误差区域[5]。由于这样形成的误差区域中含有伪相关点，故先将其称为“初始误差区域”。

2)剔除伪相关点：选中某个初始误差区域中的全部测点，用与聚类分析相同的相关系数对这些测点做相关。相关分析发现该初始误差区域中的某些测点会因相关系数低而被剔除，这些被剔除的点即为本文所述的“伪相关点”，其余满足相关条件的测点所构成的区域即是本文所要寻找的“真实误差区域”，用这样的误差区域分析装焊误差源比较可靠。

2 剔除伪相关点的实例

2.1 聚类分析

对某轿车白车身的CMM(Coordinate Measuring Machine)数据进行聚类分析。整车测点个数为672个，每个测点的误差分解成X、Y、Z三个方向[6]，每个方向的误差分量的样本长度为20个；分析时取相关系数0.8作为聚类尺度；聚类结束后最低阶聚类编号为542，该阶的测点分布见图1。

2.2 寻找初始误差区域

从低到高依次显示各阶聚类的测点分布，当显示到第503阶聚类时，测点分布状态与装焊工序相似，如图2所示。由车身装焊工艺及车体装配多层次体系结构可知，图2中的测点分布可划分成三个区域：发动机舱(图3a)、行李舱(图4a)、左右侧围(图5a)，分别对应发动机舱、行李舱焊装在地板上的装焊工序及左右侧围的合厢工序。形成的三个区域均为本文所称的“初始误差区域”。

图1 最低阶(第542阶)聚类的测点分布形态

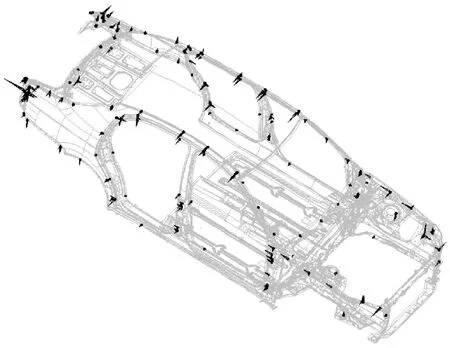
图2 第503阶聚类

2.3 剔除伪相关点

分别选中上述三个区域中的测点，仍使用0.8的相关系数在各自区域内做相关，所得测点分布形态见图3b、图4b、图5b。各区域伪相关点的去除情况如表1所示。

表1 各误差区域中伪相关点的剔除情况

从表1可以看出，“初始误差区域”中的伪相关点很多，如不剔除必然干扰对误差区域的识别，进而影响对误差源的分析；剔除这些伪相关点后的真实误差区域对误差源的识别及后续的装焊夹具调整具有较准确的指导意义。

综上所述，在用聚类分析识别装焊误差区域过程中，以相同的聚类尺度作为相关系数对各个初始误差区域各自做相关，此区域内消失的测点即为其它区域的伪相关点。利用此方法对伪相关点的剔除，只是将其不再显示，并没有剔除原始数据中伪相关点对应的数据，所以伪相关点的剔除并不影响原始数据的有效性。

图3 发动机舱区域

图4 行李舱区域

图5 左右侧围区域

3 伪相关点产生的原因及剔除机理

为探讨“初始误差区域”内伪相关点产生的原因，依次将三个误差区域中被剔除的相关点取出，分别与其它两个区域中的测点

做相关，相关系数仍为原来的0.8，所得结果如图6～图8所示。

图6中的误差点集分为两部分：其一是发动机舱区域中被剔除的伪相关点；其二是出现在另外两个区域中、但与伪相关点的相关系数达到0.8的测点。

图6 发动机舱区域中伪点的相关点集

图7 行李舱区域中伪点的相关点集

图8 侧围区域中伪点的相关点集

这解释了伪相关点混入发动机舱区域的原因：这些伪相关点与发动机舱误差区域中的其它测点不相关，但却与其它区域中的测点相关，且相关系数符合聚类尺度0.8，因此进入聚类样本测点集而混入了发动机舱区域。图7、图8中同样出现了这种现象，原因也是如此。从工序过程上看，上述三个误差区域中的冲压件都是分别装焊的，所以各区域之间的测点彼此相关是不合理的；而区域内的测点彼此之间本应该相关，出现不相关也是不合理的。

白车身的装焊误差通过抽检获得，汽车厂每天生产约200台左右白车身，抽检量为其中1～3台，故装焊误差数据处理的样本长度一般不超过20个(相当于7～20天的抽检量)[7]。由于在这7～20天里，车间不可能对装焊夹具不进行调整，故再加大样本长度已没有意义。使用如此短的样本进行数据分析，实践中经常会出现偶然的数据相关现象。

伪相关点与其它区域中的测点产生符合聚类尺度的相关性的现象可解释为偶然的数据相关性，即只是单纯的数据上的相关，其原因是样本长度有限。

4 结束语

在使用聚类分析方法寻找白车身装焊误差区域时，经常会发现区域内有伪相关点的混入而影响误差区域的识别，通过对各初始误差区域各自做相关判断某些测点消失可以剔除这些伪相关点。剔除伪点后的真实误差区域有助于提高误差源诊断的准确性。

[1]王灵犀，郝旭光，丰云秀.聚类分析方法在白车身装焊误差监控过程中的应用[J].沈阳理工大学学报，2009,28(6):57-59.

[2]陈猛,徐宗俊,郭钢.基于相关性分析方法的车体尺寸精度控制[J].重庆大学学报，2002，25(3)：6-9.

[3]胡敏，来新民，林忠钦.主成分分析方法在轿车装配尺寸偏差中的应用研究[J].中国机械工程，2002,13(6)：462-463.

[4]王学仁，王松桂.实用多元统计分析[M].上海：上海科学技术出版社，1990.

[5]林忠钦,胡敏,陈关龙，等.轿车车体装配偏差研究方法综述[J].机械设计与研究,1999,(3):58-60.

[6]杜子学.三坐标测量机在汽车整车检测中的应用[J].测试技术，1996，13(4)：33-36.

[7]S.JackHu,S.M.Wu.Identifying sources of variation in auto-mobile body in white assembly using of Principal Components Analysis[C].Transactions of AMRI/SME,1992.

(责任编辑：赵丽琴)

Excluding Spurious Correlation Points in Process of Research BIW Assembly Error

WANG Lingxi,LIU Qingkun,BU Zhanhang

(Shenyang Ligong University,Shenyang 110159,China)

The process of using clustering analysis to identify the assembly error sources of BIW,many pseudo-related points usually were frequently found in inaccurate areas.In this paper the method to use correlation analysis in these areas to exclude these pseudo-related points is proposed.After correlation analysis the points that disappeared are pseudo-related points.On the other hand,the points that didn’t disappear comply with the conditions of clustering and these points constitute the true error region.The results show the proposed method can exclude pseudo-related points effectively and detect areas more accurately.

clustering analysis;body-in-whit;pseudo-related points;correlation analysis

2014-09-01

王灵犀(1956— )，男，教授，研究方向：汽车试验与仿真研究.

1003-1251(2015)06-0062-04

TP206；U463.8

A