基于内生增长模型的技术水平与经济增长之间关系研究

王丽丽，汪潘义

(合肥学院 数学与物理系，安徽 合肥 230601)



基于内生增长模型的技术水平与经济增长之间关系研究

王丽丽，汪潘义

(合肥学院 数学与物理系，安徽 合肥 230601)

[摘要]文章以确定性的边干边学模型和R&D模型为背景，将随机扰动和技术水平引入其中，得到包含劳动力投入、物质资本和技术水平的随机内生经济增长模型.因此原模型中的要素积累方程从ODE过渡到SDE，并对其作某些定性的分析.进而运用二次Liapunov函数等方法对随机边干边学模型的零解的稳定性及其平稳分布进行了有益的探索，得出了一些有意义的结果。

[关键词]技术水平； 内生增长； 二次Liapunov函数； 平稳分布；经济增长

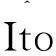
1模型

对R&D模型作如下修正：技术开发不是在独立的R&D部门中进行，而是作为生产部门的副产品出现。这意味着，每个生产单元对于技术进步都作出了贡献，且贡献量决定于其产出水平。因此，我们将技术水平A表示为资本存量K的函数：A=BKξ，B与ξ是正常数。生产部门生产物质产品，其生产函数为：

(1)

其中CY是正常数，0<α<1，α′=1-α。在生产过程中，要素资本K，劳动力L在生产部门与R&D部门按固定比例配置，这些比例已吸收进CY中而未直接表现出来。与确定性模型比较，一个关键差别是，Y是平均产出(或期望产出)，以φK表示资本K的期望增长率，且假定y=φK=s(Y/K)，s∈(0,1)是常数储蓄率。设K，L服从如下随机增长方程：

( (2)

其中n是非负常数，duK,duL是Brown运动；将A=BKξ代入(1)得

((3)

利用y=s(Y/K)，式(2)与(3)，计算得出

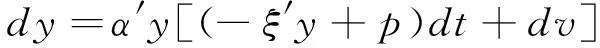
((4)

其中

dv=-ξ′duK+duL

(4)就是SDE。若dv=0，则(4)退化为确定性边学边干模型的微分方程：

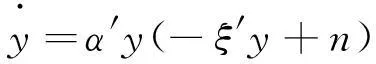
((4)

2稳定性分析

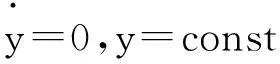
现在考虑SDE(4) 。显然有零解，现引入二次Liapunov函数来讨论其零解的稳定性。取D=(0,∞)，利用随机微分方程的方法用于方程(4)分别得到

与

经整理后，以上条件可分别简化为

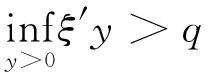
((5)

与

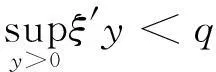
((6)

其中

下面分几种情况讨论:

(ⅰ)设0<ξ<1，则ξ′>0，条件(5)必不满足，而条件(4)相当于q<0，即

((7)

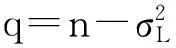
(ⅲ)设ξ>1，则ξ′<0，条件(5)必不满足，而条件(6)相当于q>0，即

((8)

3平稳分布

现在我们来求由系统(4)决定的变量y(y>0)平稳分布。利用计算公式[9]:

用α′y(p-ξ′y)和α′y分别代替f和g,首先算出：

以π(y)记所求的平稳分布，则

故得

((9)

为使π(y)有意义，必需β，ω>0，这相当于

((10)

4平稳值与均衡值分析

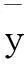
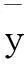
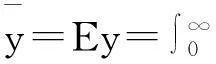
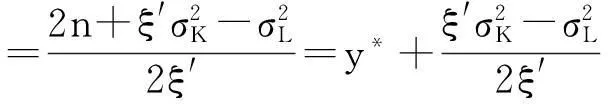
于是有以下结论：

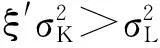
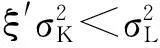
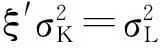
[参考文献]

[1]Solow R M. A contribution to the theory of economic growth [J]. Q.J. Economic, 1756,70:65-94.

[2]Turnovsky SJ. Fiscal police, elastic labor supply and endogenous growth [J]. Journal of Monetary Economics, 2000, 45: 185-210.

[3]Jurgen Mecki, Stefan Zink. Solow and heterogeneous labor: a neoclassical explanation of wage inequality [J]. The Economic Journal, 2004, 498: 825-843.

[4]Jonathan Temple. The long-run implications of growth theories [J]. Journal of Economic Surveys, 2003, 3: 497-510.

[5]Bjarne Jensen S. Saving rates, trades, technology and stochastic dynamics [J]. Review of Development Economic, 2001, 2: 182-204.

[6]Yaung A. Growth without scale effects [J]. Journal of Political Economics, 1998, 106: 41-63.

[7]Jones L E,Manuelli R E. The sources of growth [J]. Journal of Economic Dynamics & Control, 1997, 21: 75-114.

[8]King R G,Rebelo S. Transitional dynamics and economic growth in the neoclassical model [J]. American Economic Review, 1993, 83: 908-931.

[9]Arnold L. Stochastic Differential Equations: Theory and Applications [M]. New York: John Wiley & Sons, 1974:78-101.

[10]Gihman I, Skorohod A V. Stochastic Differential Equations [M]. New York: Springer-Verlag, 1972:23-69.

Research on Relationship between Economic Growth and Technological

Level Based on Endogenous Growth Model

WANG Lili ,WANG Panyi

(HefeiUniversity,Hefei230601,China)

Abstract：Stochastic disturbance and technological level are introduced into deterministic growth model of “learning by doing and R&D”. The stochastic endogenous growth model with the labor input, physical capital and technological level is obtained. The accumulation equations of production factors accordingly toSDE from ODE, on which qualitative analysis is built. Moreover, the method of the quadratic Liapunov function and the others are used to analyze the stability of zero solution of the stochastic model of Learning by doing and to calculate the stationary distribution of the model. Helpful results are obtained.

Key words：Technological level; Endogenous growth; Quadratic Liapunov function; Stationary distribution; Economic growth

[中图分类号]F22

[文献标识码]A

[文章编号]1674-2273(2015)06-0011-02

作者简介][第一 王丽丽(1982-)，女，安徽蚌埠人，硕士，合肥学院讲师，研究方向：金融数学。

[基金项目]国家级大学生创新创业训练计划项目(201511059033)

[收稿日期]2015-08-02