基于改进的各向异性SUSAN算法的MEMS微结构图像滤波

基于改进的各向异性SUSAN算法的MEMS微结构图像滤波

罗元，蔡祖嫘，张毅

(重庆邮电大学 重庆高校光纤通信技术重点实验室， 重庆 400065)

摘要：为了改善在滤除微机电系统微结构图像的噪声时导致边缘模糊的问题，提出了一种改进的各向异性SUSAN滤波算法。该方法用独立强度传播模型决定长短轴的方差，由该点的梯度方向决定滤波器的长轴方向，由局部图像的灰度值与核值的差构成的局部均值构成SUSAN滤波器的自适应阈值，从而构建出各向异性SUSAN滤波器。该算法在平滑图像同时能保持图像的边缘特征。结果表明，各向异性SUSAN滤波器能够很好地降噪并保持图像的边缘信息。

关键词：图像处理;模糊图像;各向异性滤波;SUSAN滤波; 微机电系统

E-mail:luoyuan@cqupt.edu.cn

引言

微机电系统(micro electromechanical systems，MEMS)包含一些如谐振器、振动陀螺、加速度计、光开关等可动部件。在用机器视觉方法高精度测量其动态特性时，由于成像系统获取图像时会因为电子、光子、元器件本身或媒介扰动等产生噪声影响数字图像质量[1]，而且通常图像采集的频率低于MEMS可动部件的运动频率，会造成在运动方向的模糊，因此获得的MEMS图像通常是含噪的且可动部件的边缘通常会形成一条模糊带。在对MEMS图像进行去噪的预处理时，使用常用的各向同性去噪方法如均值滤波、高斯滤波等在平滑噪声的同时，也会使边缘等细节信息模糊，使得原本模糊的边缘轮廓更不清晰，对后期精确测量MEMS微结构的振幅、运动速度、品质因数等参量有很大的影响。为解决图像滤波中保持重要特征的问题，PERONA和MALIK提出各向异性微分方法，方向性强，但同时表现出病态和不稳定[2]；WITKIN提出了多尺度空间理论;现在有不少基于多尺度空间理论的滤波器[4]，不需要图像先验知识，但对图像平坦处和边缘处理相同，仍无法避免对边缘的平滑。SUSAN滤波算法[5]对滤波窗口内的像素点进行了比较处理，故在滤波时能够在一定程度上保持图像的特征结构，在对弱小目标的保护方面已有较好的应用[6]，但该算法在图像平滑处理时采用了各向同性的高斯函数，仍会有细节信息丢失。

为了提高边缘相对规则、具有方向性但较模糊的MEMS微结构图像的测量精度，本文中提出了一种改进的各向异性SUSAN滤波算法，该算法采用改进的Geusebroek快速各向异性高斯滤波器[7]替代了SUSAN滤波算法中原有的高斯滤波器，从而构成了各向异性的SUSAN滤波器。因为SUSAN算法本身对边缘敏感对噪声不敏感，再加上各向异性高斯滤波器的引入，使得该方法能够很好地平滑图像噪声，同时能够更好地保持图像的微结构特征,适当地选择参量还能够在一定程度上改善图像质量。这对下一步的MEMS微结构动态测量具有重大意义。

1SUSAN算法

SUSAN算法是由SIMTH和BRADY首先提出的,SUSAN算法可以用于边缘、角点特征检测和滤波两种用途[8-9]。其算法的检测原理是基于单瓣段同化核(univalve segment assimilating nucleus,USAN)检测准则建立的。该方法称在模板中心的像素值为核值，当模板在图像上移动,若模板内其它像素点与核值的差小于阈值时则视为与核值同值，满足这个条件的点构成的区域叫做USAN区，即吸收核值相似区。根据以上定义可知,USAN区的面积在图像平坦区域最大，在角点处最小。USAN的面积计算采用如下比较函数：

式中,c(x,y)为比较函数的值，I(x0,y0)为模板中心像素的灰度，I(x,y)为模板内除核值外的任意一点的灰度值；t为阈值，代表能够检测出边缘的敏感度,也是对噪声的容限度。图像对比度越低，t的值应取得越小，才能提取出图像的特征，反之图像对比度高，则t的值应增大。另外为了保持算法的各向同性，在算法提出时选择了圆形模板，但在实际的数字图像处理中一般采用5×5模板或者37pixel模板。

SUSAN滤波算子是由相似比较函数与高斯函数的乘积构成，它利用了高斯函数在时域和频域上的良好平滑能力，同时够保持目标结构，从而能在滤波的同时较好地保持图像细节特征信息。为便于计算机处理，滤波时常采用的相似比较函数可参见参考文献[7]。

则图像处理中完整的SUSAN滤波算子表达式为：

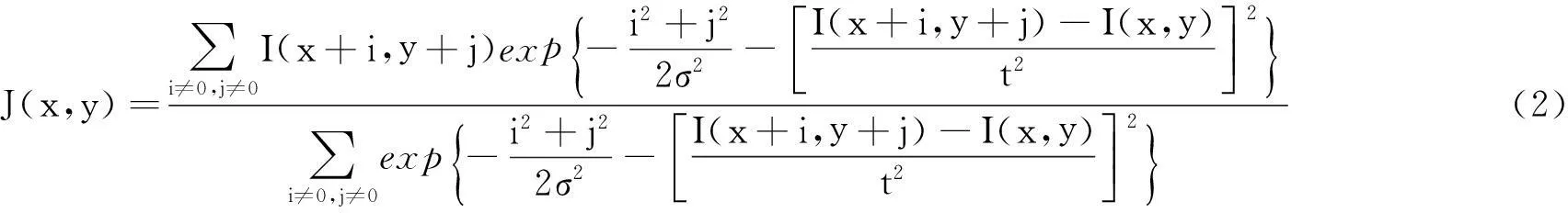
式中,x，y为图像内任意像素点的坐标；i，j为模板内任意像素点的遍历值；σ为滤波器的方差，其大小影响滤波器的平滑效果，太大会丢掉图像细节，太小又起不到平滑效果。根据经验，一般取σ=4.0[6]就能取得较好的滤波效果。

由于滤波过程是利用滤波模板中满足与核值相同的条件的点来参与运算的,因此该算法具有去噪且保护图像细小特征的特点。但对于边缘较为规则且模糊具有方向性的MEMS微结构图片，要获得高精度的边缘信息，该算法还需进一步改进。

2改进的各向异性SUSAN滤波算法

2.1　各向异性SUSAN算法

由于SUSAN算法是由比较函数和高斯函数结合的滤波算子，虽然较高斯滤波的边缘保持性有一定提高，但从滤波性能来讲仍是一个各向同性的算法，而一幅图像通常拥有不同类型的边缘，采用各向同性算法必定会丢失很多信息。本文中的各向异性SUSAN滤波算法改进了GEUSEBROEK提出的快速各向异性高斯滤波算法。在参考文献[10]中，WANG等人也改进了这种快速各项异性高斯滤波算法，但方向角的确定计算较为复杂，且由于MEMS微结构形边缘相对规则，本文中算法简化了方向角的计算。

在2维图像域，各向同性滤波算子表达式显示，图像边缘横向和纵向扩散速度相同，因此该算子为各向同性；各项异性的滤波算子改变了横向和纵向的扩散速度，表达式可参见参考文献[10]。

实际应用中图像边缘的方向通常并非都是规则的，此时设边缘方向角为θ，如图1c所示。

各向异性高斯滤波器在2维平面的投影是一个椭圆，椭圆的轴线与坐标轴还有一个任意旋转角θ，则以椭圆中心和其长短轴建立的新坐标系u-v与原x-y坐标系的转换关系表达式可参见参考文献[10]。

Fig.1　Projection of 2-D coordinate of three kinds of Gaussian filters

a—Gaussian filterb—anisotropic filter in fixed directionc—anisotropic filter in any direction

各向异性高斯滤波器的表达式为：

式中,σu,σv分别为滤波器在u,v方向上的尺度。

实际应用中，当滤波器的长轴方向与边缘垂直时,滤波器会使边缘模糊化达到最大；当滤波器长轴与图像边缘重叠时，滤波器处理才能达到最优。由于图像边缘类型不同，当图像边缘不是一条直线时，为保证滤波效果，使滤波器长轴与边缘切线方向相同。考虑到这一情况，本文中的滤波器长轴方向由所在位置的灰度值梯度方向决定。因此图像中点(x,y)的梯度方向θ⊥可以表示为：

式中,Dx(x,y),Dy(x,y)为点(x,y)处的水平方向和垂直方向的梯度值，计算式如下:

式中,r是滤波模板的半宽，f(x,y)为点(x,y)的灰度值。

因为θ⊥为近似法线方向，则滤波方向角θ的表达式为：

将(6)式代入(3)式可以得到各向异性高斯滤波算子为:

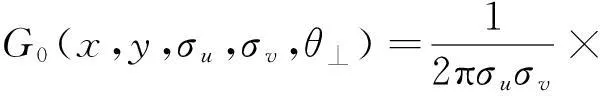
则各向异性SUSAN滤波器的算子为：

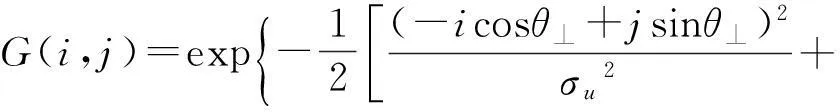
2.2　参量的选取和优化

阈值t表示能检测边缘点的最小对比度，对不同的噪声情况的图像应去不同的值，作者采用滤波窗口内图像灰度的平均值来确定t值的大小，如下式所示：

如前面介绍，在传统的SUSAN滤波算子中，一般取σ=4.0就可以取得较好的滤波效果，但是对于图像中不同的区域，灰度分布不一致，还可以对这个参量进行改进。在对各向异性滤波器尺度确定研究中，已提出不少方法，如方差最小的原则来确定各像素处的尺度的方法,还有灰度共生矩阵的惯性矩特征值来确定尺度等方法等，但以上方法却很少在实际中应用，因为它们存在初始参量需要人为给出和计算量大的缺点。为简化计算，本文中采用了CORNSWEET[11]等人根据人类视觉模型提出的独立强度传播模型，得到一种简单的长轴尺度定义方法：

式中,I(x,y)是图像的灰度，I(x,y)的值归一化为[0,1]区间。则短轴尺度σv可由下式表示：

式中,D是一个窗口内中心的方差;k为比例因子，经验值取为20可以达到很好的滤波效果。

3实验及分析

采用各向异性SUSAN滤波算子对MEMS微结构图片进行处理，本文中选择7×7的滤波模板，对图像某一点计算水平和垂直梯度，以确定长轴的方向，对该点的邻域计算区域方差以确定长轴方差σu，利用(11)式确定短轴方差，利用该点邻域与均值差值的1阶范数确定SUSAN滤波器的阈值参量t，然后用构造好的SUSAN滤波器与图像进行卷积，一次处理完图像所有点即可。

实验中所用的输入图像是含有高斯噪声的MEMS微结构频闪照片，像素尺寸为170×370，可以看到,插值梳齿因运动而导致了沿振动方向的模糊，水平方向的边缘因为运动造成的模糊使边缘宽度增加，给后续精确测量带来不便。

关于图像质量的客观评价，作者采用了最为常见和广泛使用的基于像素的均方差E和峰值信噪比PSNR两个方法来对处理后的图像进行定量分析。

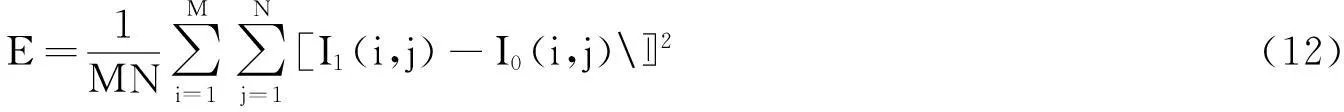
式中,M和N为图像的尺寸，I1(i,j)与I0(i,j)分别是处理后的图像和原图。从定义来看，均方差公式反应的是原图像与处理后的图像的近似程度，其值越小表示处理后图像与原图越相近，说明滤波器性能越好；PSNR是到达噪音比率的顶点信号，其值越大，就代表失真越少。表1中为3个处理后图像的指标比较。

Table 1　Comparison between E and PSNR of three filtering algorithms

从处理后的图像(如图2所示)来看，SUSAN滤波采用传统高斯滤波算子，虽然滤除了噪声，但是图像的边缘并没有很好地保持，造成了一种图像的朦胧感；Geusebroek算法能够在滤除噪声的同时对边缘起到一定的保持作用，由于它只能保持一个θ方向，在不太规则的插值梳齿的边缘处仍非常模糊；本文中的算法不仅能够滤除噪声，而且图像也更清晰，且E与PSNR优于前两种算法，也从客观上反应出本文中的算法能使边缘更清晰。但本算法在改善滤波性能的同时也增加了运算量，还可以在提高速度上进一步改进。

Fig.2　Experimental results

a—MEMS stroboscopic image with noiseb—SUSAN filterc—Geusebroek filterd—filtering with the proposed method

4结论

在SUSAN滤波的基础上，结合了改进的各向异性高斯滤波器，得到了一种改进的各向异性SUSAN滤波算法。对各向异性SUSAN滤波中长短轴尺度的参量优化，能够使滤波器在各个位置上根据图像的特点自适应变化,因此实现在去噪的同时最大限地保留了边缘等重要信息，使得模糊图像中的边缘尽可能保留。对于后续更精确地测量MEMS微结构动态参量有很大的意义。

参考文献

[1]DING M, XU X. CCD Signal noise model simulation and test[J]. Instrument Technique and Sensor,2012(1):64-67(in Chinese).

[2]PERONA P, MALIK J. Scale-space and edge detection using anisotropic diffusion.IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990,12(7):629-639.

[3]WITKIN A P. Scale-space filtering:a new approach to multi-scale description//Acoustics, Speech, and Signal Pocessing, IEEE International Conference on ICASSP’84.New York,USA:IEEE,1984:150-153.

[4]LU Zh L,LI R L,LI T,etal. Infrared image denoising based on total variation theory [J]. Laser Technology, 2012, 36(2):194-197(in Chinese).

[5]SMITH S M, BRADY J M. SUSAN-a new approach to low level image processing [J] . International Journal of Computer Vision , 1997, 23(1):45-78.

[6]JING L, PENG Zh M,HE Y M,etal. Infrared dim target detection based on anisotropic SUSAN filtering [J] . High Power Laser and Particle Beams, 2013,25(9):2208-2212(in Chinese).

[7]GEUSEBROEK J M, SMEULDERS A W M, VAN de WEIJER J. Fast anisotropic gauss filtering [J] .IEEE Transactions on Image Processing,2003,12(8):938-943.

[8]WENG M Y, HE M Y. Integrated feature and its application to image detection and matching [J]. Journal of Image and Graphics,2007, 12(1): 121-126(in Chinese).

[9]YU H L, SU H Q, WANG Y,etal.Application of SUSAN corner detection and matching algorithm in high temperature deformation measurement[J].Acta Aeronautica et Astronautica Sinica, 2013,34(5):1064-1072(in Chinese).

[10]WANG H Y, ZHANG K, LI Y J. Anisotropic gaussian filtering for imfrared image [J]. Journal of Infrared and Millimeter Waves, 2005, 24(2): 109-113(in Chinese).

[11]CORNSWEET T N, YELLOTT J I, Jr. Intensity-dependent spatial summation[J]. Journal of the Optical Society of America, 1985, A2(10): 1769-1786.

MEMS microstructure image filtering based on

improved SUSAN anisotropic algorithm

LUOYuan,CAIZulei,ZHANGYi

(Key Laboratory of Optical Fiber Communication Technology of Chongqing Education Commission, Chongqing University of Post and Telecommunications, Chongqing 400065, China)

Abstract：To improve the blur edge of micro electromechanical systems(MEMS) microstructures image caused by filtering the noise, an improved anisotropic SUSAN filtering algorithm was proposed. In this method, the variances of long axis and short axis were determined in accordance with the independent density spread model, the long axis direction was determined by the gradient direction of the point and the SUSAN filter threshold was determined by the partial average difference between gray value of local image and nucleus. So anisotropic SUSAN filter was constructed. The filter can maintain the edge features as well as process the image smoothing. The experimental results show that anisotropic SUSAN filter could reduce the noise and preserve the edge information at the same time.

Key words:image processing; fuzzy image; anisotropic filtering; SUSAN filtering; micro electromechanical systems

收稿日期：2014-01-14；收到修改稿日期：2014-02-28

作者简介：罗元(1972-)，女，博士，教授，主要研究方向为数字图像处理、信号与信号处理。

基金项目：国家自然科学基金资助项目(51075420)

中图分类号：TP391.4

文献标志码：A

doi:10.7510/jgjs.issn.1001-3806.2015.01.017

文章编号：1001-3806(2015)01-0085-05