基于Verhulst与线性回归组合模型的港口吞吐量预测研究

代雯强　杨　珩

(中交第二航务工程勘察设计院有限公司　武汉　430060)

基于Verhulst与线性回归组合模型的港口吞吐量预测研究

代雯强杨珩

(中交第二航务工程勘察设计院有限公司武汉430060)

摘要由于港口吞吐量预测的复杂性，在许多情况下，单纯利用一种特定的预测方法进行预测往往具有片面性，为尽可能使预测结果具有较高可信度，基于“误差平方和最小”为最优准则，建立灰色Verhulst时序残差修正模型与一元线性回归模型的组合模型，将其用于某港口货物吞吐量预测，经验证组合模型具有较好的预测效果，并对该港口未来3年的货物吞吐量进行了预测。

关键词吞吐量预测时序残差修正Verhulst模型线性回归模型组合模型

目前，港口吞吐量的预测方法有很多，定量预测法主要分为2大类：时间序列法和因果关系法。前一类预测法包括指数平滑法、自回归法、移动平均法、灰色预测法等；后一类预测法包括回归分析法、系统动力学法、投入产出法等[1]。

考虑到在中长期港口吞吐量预测中基于时序残差修正的Verhulst模型可以很好地解决吞吐量增长到比较饱和阶段的预测问题[2]，以某港为例，基于时序残差修正Verhulst模型和一元线性回归模型，以“误差平方和最小”为准则建立组合预测模型，并通过对模型精度进行分析，选择最优模型，对港口吞吐量做出预测。

1数学模型

1.1　时序残差修正Verhulst模型

灰色预测最大的优点是以微分方程形式描述模型，能够反映出事物发展的连续性，较适用于中长期的预测规划，而Verhulst模型可描述未来年具有饱和状态的预测[2]。这些均符合港口吞吐量预测的特点，因此，选用灰色Verhulst模型对吞吐量进行预测是合适的。

1.1.1灰色X(0)-Verhulst 模型

X(0)表示n年的吞吐量数据序列：X(0)= (x(0)(1)，x(0)(1)，…，x(0)(n))

对X(0)做一次累加生成(即1-AGO生成)得到X(1)= (x(1)(1)，x(1)(1)，…，x(1)(n))。

设非负原始数据序列，其中

(1)

取x(1)(1)=x(0)(1)，则灰色Verhulst模型的时间响应函数为

(2)

利用一次累减还原计算，得到原始数据序列拟合值：

(3)

式(2)，(3)即为x(0)-Verhulst模型，x(0)为历年吞吐量数据序列，依据式(2)，(3)和x(0)可确定参数a，b，进而得到港口吞吐量预测值。

1.1.2Verhulst 模型的时序残差修正

利用上述x(0)-Verhulst模型计算并预测吞吐量存在一定误差，且时序k按等时序处理。为提高模型精度，可对时序k进行残差修正。假设k存在残差ek，令

(4)

(5)

建立时序残差序列ek(0)的GM(1,1)模型，即

(6)

(7)

由式(2)，(3)可对吞吐量进行初步预测，再由式(6)，(7)对时序k进行残差估计，进而对吞吐量预测值进行修正，最终得到未来年的吞吐量预测值。

1.2　线性回归模型

回归分析是通过研究与预测目标相关的影响因素，并通过因素统计资料运用最小二乘法拟合[3]。采用一元线性回归模型预测港口吞吐量，考虑港口吞吐量与国内生产总值(GDP)往往具有较好的相关性，选择GDP作为相关关系分析中的自变量，以港口吞吐量作为因变量建立相应的线性回归模型如下：

X(t)=aY(t)+b

式中：t为年份；X(t)为港口吞吐量；Y(t)为GDP。

1.3　“误差平方和最小”的组合预测模型

(1) 组合预测模型建立。设某一预测问题在某一时段的实际值为Y(t)，基于上述2种单向预测，分别设2种单向预测法预测吞吐量值分别为V(0)(t)，X(0)(t)(t=1,2，…，n)，根据参考文献[4-5]，可建立如下方程组：

(8)

求解该方程，可以得到w1，w2，则“误差平方和最小”的组合预测模型目标函数为：

(9)

(2) 模型精度。采用残差检验，计算其模型精度η。

2某港吞吐量预测

以某港为例，选取某港2008～2013年港口货物吞吐量数值及国内生产总值GDP数值作为建模数据(见表1)，先对模型进行验证，包括时序残差修正Verhulst模型、一元线性回归模型以及基于“误差平方和最小”的组合预测模型。验证完毕后，对3个模型进行比较和分析。

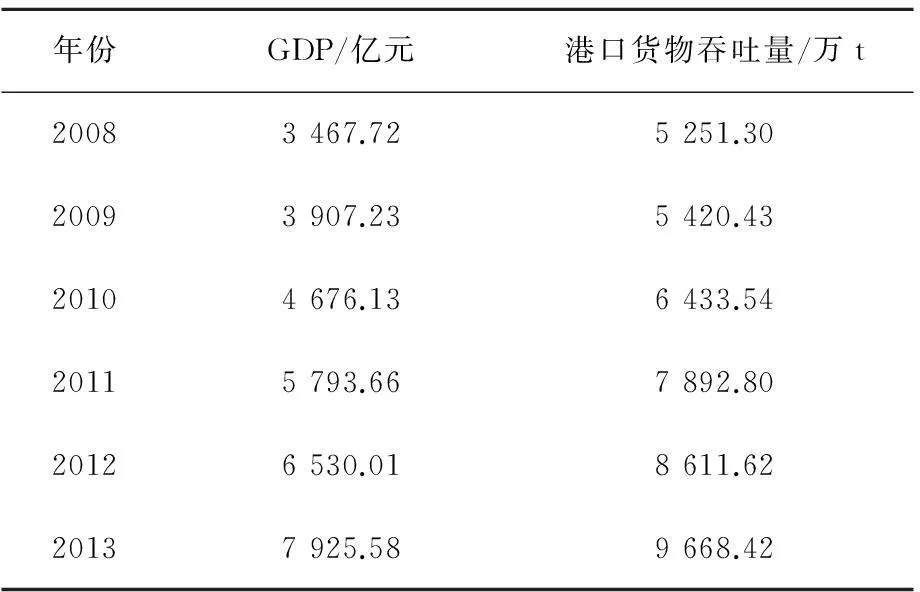
表1　某港2008-2013年港口货物吞吐量及GDP统计表

2.1　时序残差修正Verhulst模型

根据1.1计算得，时序残差修正Verhulst模型中a=-0.139 250，b=4 549.889，预测结果见表2。

经模型精度检验，模型精度η=0.972>0.9，残差检验结果为很好。另外，采用后差检验法，经计算c=0.000 012 4<0.35，p=1，可知模型精度1级(好)，可用所建的模型进行吞吐量预测。

2.2　一元线性回归模型

考虑港口吞吐量与国内生产总值(GDP)往往具有较好的相关性，选择GDP作为相关关系分析中的自变量，以港口吞吐量作为因变量建立相应的线性回归模型如下：

X(t)=0.975Y(t)+1933.603

(10)

式中:t为年份；X(t)为港口吞吐量；Y(t)为GDP。

经相关系数检验，该回归模型显著性较好。预测结果见表3。

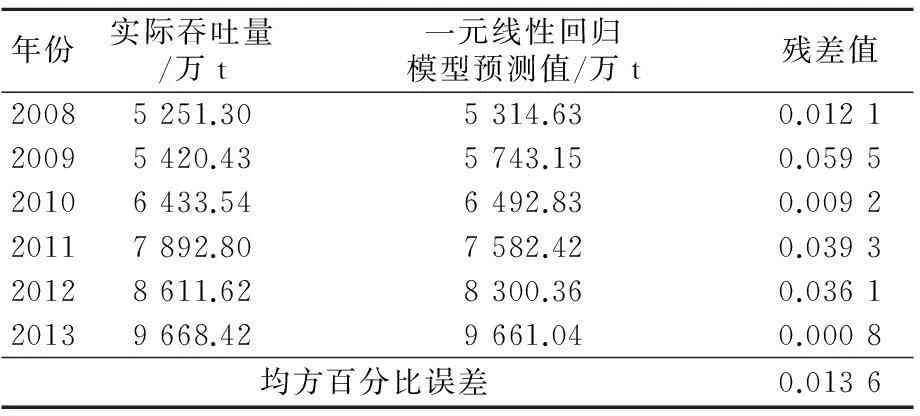
表3　一元线性回归模型预测值(万t)及精度

2.3　“误差平方和最小”的组合预测模型

根据上述2种模型的预测结果，参考公式(10)建立方程组如下：

求解该方程，可以得到w1=0.557 595 101，w2=0.442 404 899。经计算，时序残差修正Verhulst模型预测的权系数为0.557 595 101，一元线性回归模型预测的权系数为0.442 404 899。将其代入式(9)，得到组合预测模型：

0.442 404 899X(0)(t)t=1,2,…,n

分别将t=1, 2,…,n代入即可得到组合模型预测的吞吐量，见表4。

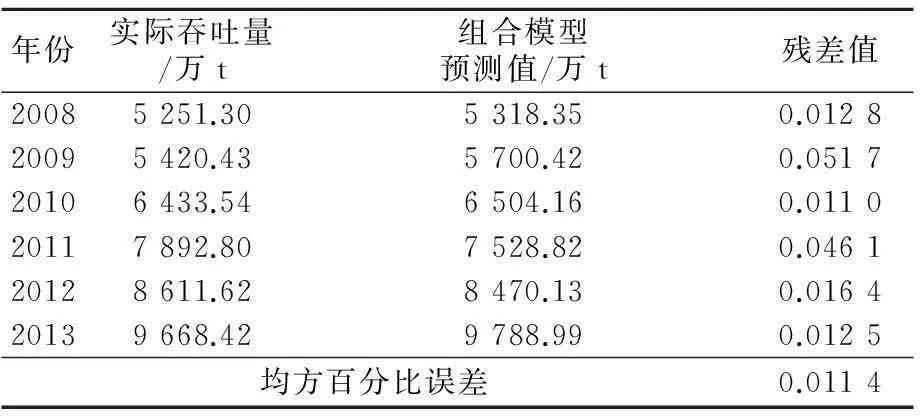
表4　组合模型预测值(万t)及精度

采用残差检验，计算其模型精度η=0.973>0.9，残差检验结果为很好，组合模型可用于吞吐量预测。

2.4　模型评价

根据上述结果，从单一模型来看，时序残差修正Verhulst模型的预测效果好于线性回归模型，表明其更能反映出该港目前的吞吐量发展趋势。

组合预测模型的均方百分比误差最小，预测的精度较单一的预测模型有所提高，其应作为该港吞吐量预测的最优模型。

2.5　运用组合模型预测该港港口吞吐量

最后运用3种模型预测2018~2020年共3年某港港口货物吞吐量。预测结果见表5。

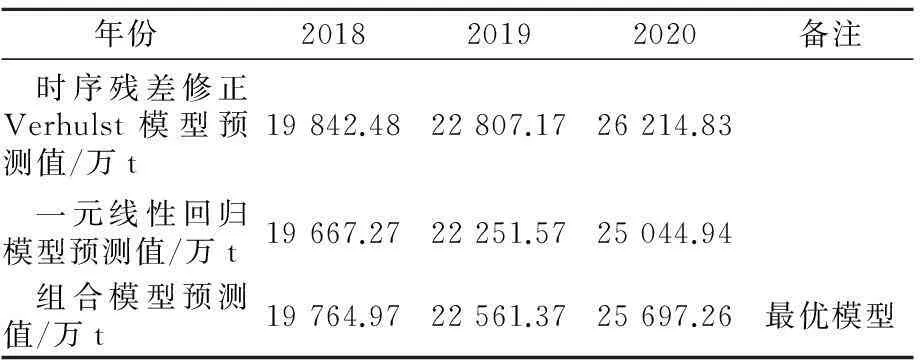
表5　某港2018~2020年港口货物吞吐量预测值

3结论

(1) 时序残差修正Verhulst模型可较好地描述未来年具有饱和状态的港口吞吐量预测，其预测精度相较于线性回归模型有所提高，表明其更能反映出该港目前的吞吐量发展趋势。

(2) 基于时序残差修正Verhulst模型和一元线性回归模型，以“误差平方和最小”为准则建立组合预测模型新建的组合模型，经验证组合模型具有较好的预测效果。

(3) 经比较，建立的组合预测模型均方百分比误差最小，预测的精度较单一的预测模型有所提高，其应作为该港吞吐量预测的最优模型。

(4) 通过对3种模型精度进行分析，选择最优模型，尝试对港口吞吐量做出预测，由预测值可以看出，未来某港的货物吞吐量仍将呈上升趋势，2018相比2013年递增幅度达到15%，2019年、2020年增幅为14%。

参考文献

[1]翟希东.港口集装箱吞吐量预测模型研究[D].大连：大连理工大学，2006.

[2]叶剑，宋向群，郭子坚.港口吞吐量预测的时序残差修正Verhulst模型[J].水运工程，2004(12)：18-22.

[3]刘明维，王多银.港口货物吞吐量预测方法探讨[J].水运工程，2005(3)：53-55.

[4]朱超.组合预测在港口吞吐量预测中的应用研究[J].港工技术，2006(9)：10-12.

[5]张浩.基于最优线性组合的港口集装箱吞吐量预测方法[J].武汉理工大学学报:交通科学与工程版,2007(2):373-376.

Port Throughput Forecasting Method Based on Time Series Error

Corrected Verhulst Model and Linear Regression Combined Model

DaiWenqiang,YangHeng

(CCCC Second Harbor Consultants Co., Ltd., Wuhan 430063, China)

Abstract：Owing to the complexity of port throughput forecast, using one prediction technique always is partial in many cases. In order to increase the reliability of result, aiming the square sum of error, the combined model of gray Verhulst series error correction model and simple linear regression model is constructed to forecast the port throughput capacity. It is proved that combination model's prediction is effective and the port throughput capacity in the next 3 years is predicted.

Key words:throughput forecasting; verhulst model on time series error correction; linear regression; combined model

收稿日期：2015-04-15

DOI 10.3963/j.issn.1671-7570.2015.03.059