预制破片弹对装甲目标毁伤效能计算
聂 浩,吴正龙
(陆军军官学院,合肥 230031)
目前我军各主战火炮都配备了预制破片弹,预制破片具有形状可控、分布密集、毁伤能力强等优点,在对付装甲目标时其优点尤为明显。然而,目前预制破片弹的毁伤计算研究相对滞后,基本沿用了自然破片弹的毁伤研究方法,没有对预制破片弹特点进行分析研究,特别是没有预制破片场的弹道性能进行专门研究。针对此问题,根据毁伤元特点,对预制破片弹毁伤效能进行计算研究。
根据自然破片战斗部的经验,除直接命中外,在正常炸目距离情况下,预制破片战斗部的冲击波对装甲目标一般不会造成明显伤害;另一方面,预制破片战斗部头部和尾部的自然破片毁伤效能低、散布大,对装甲毁伤可也以忽略;因此,对付装甲目标,预制破片是主要毁伤元。
1 破片场计算
1.1 破片速度
预制破片由炸药爆炸形成的冲击波驱动,影响速度的因素很多:质量、尺寸、装药量、相对位置等,一般用格尼公式计算破片速度[1]
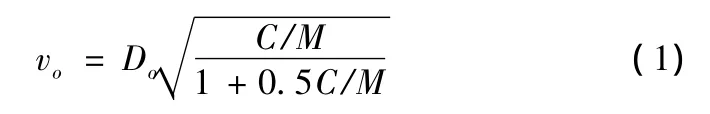
式中:vo为破片初速;D0是炸药格尼常数,用来描述炸药性质,为无量纲常数;C为炸药质量;M为战斗部外壳质量。
对于预制破片弹,战斗部头部和尾部产生自然破片,预制破片仅存在于圆柱部,在计算预制破片速度时,炸药、壳体质量按圆柱部部分计算。
战斗部在弹道末端爆炸,预制破片受冲击波驱动而产生速度,此时破片速度应考虑战斗部的速度叠加,因此破片的速度 vfo为
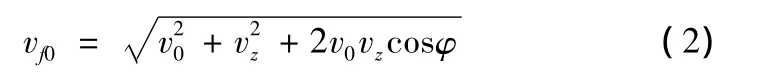
式中:vz是战斗部速度;ψ是战斗部轴线与静爆速度夹角。
1.2 破片速度衰减
由于空气阻力的影响,破片在空气中速度逐渐衰减,速度可由表示为

式中:vf是破片速度;Ca是空气阻力常数;ρa是空气密度;sf迎风面积;Rd是破片运动距离。
1.3 破片分布
战斗部爆炸后,破片在空间呈球面分布,破片在战斗部两端分布较少,在战斗部中间分布比较集中,一般以炸药爆心为顶点,将包含90%破片的角称为飞散角。破片飞散角Δψ=ψ1+ψ2,ψ1、ψ2为破片轴向两端飞散方位角,其大小可以表示为
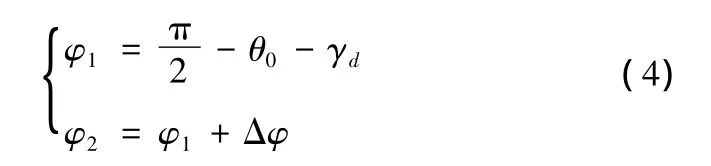
式中,γd为战斗部外壳法线与弹轴夹角。
根据泰勒公式可得出破片速度方向与外壳法线夹角θo为
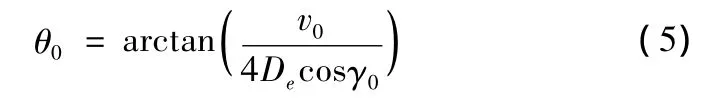
式中,γ0是炸药爆轰波的阵面法线与弹轴夹角。
战斗部在运动中爆炸时,考虑到战斗部速度,破片飞散角需要在静态飞散角基础上加以修正,设动态飞散方位角为ψ',则 ψ'为
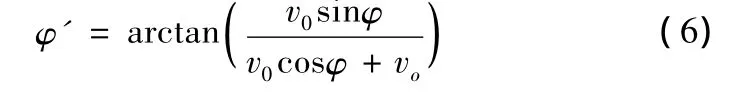
由式(6)可得破片飞散区间为
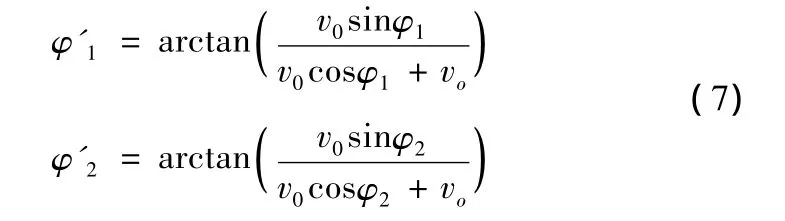
1.4 破片密度
忽略重力影响,认为破片在战斗部周向均匀分布,在轴向呈正态分布,则分布概率为
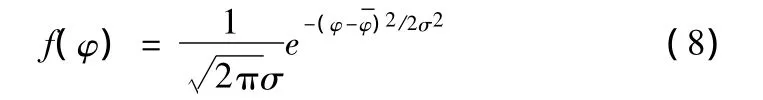
2 目标易损性分析
2.1 目标毁伤树
以某型装甲运输车为例[2],将该装甲车看作一个系统,按照功能,将其划分为外装甲、底盘系统、牵引系统和通信系统、电气系统、武器系统等系统,每个子系统包含若干要害部件(如图1所示)。
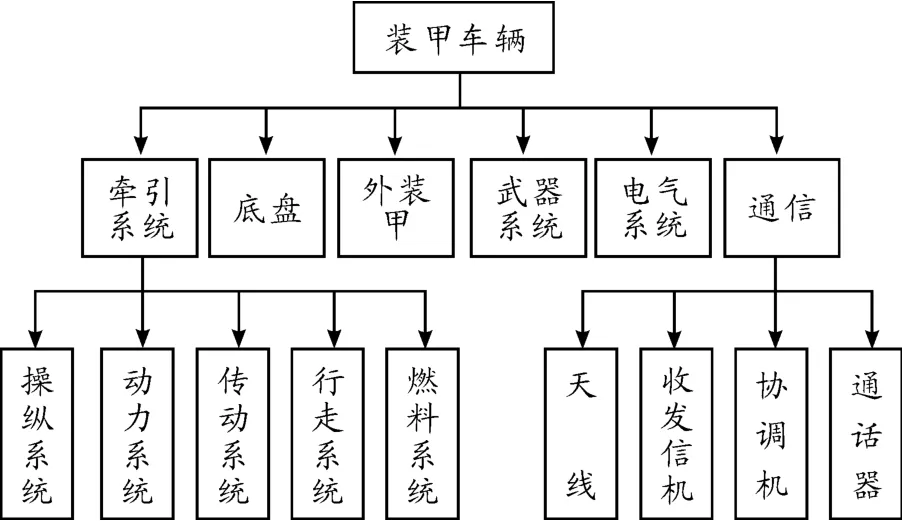
图1 装甲车部分毁伤树框图
2.2 目标毁伤级别
按照毁伤不同部件对装甲车辆的影响,将装甲车辆毁伤分为M、F、K 3个级别:M级为装甲车辆抛锚,不能行驶或行驶不受控制;F级为装甲车辆武器或武器保障装备受损,丧失火力;K级为装甲车辆受重创,完全丧失作战能力,没有维修价值。
2.3 毁伤准则
部件毁伤准则是判用来断部件是否毁伤的判据,毁伤准则描述了部件毁伤与毁伤元之间的相互关系,一般用毁伤函数表示,毁伤函数为
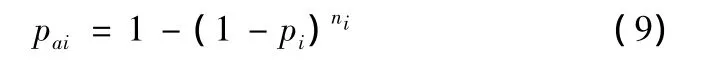
式中:pai为第i个部件受破片场作用而造成的毁伤概率;pi为部件受破片i作用而毁伤的概率,将在4.3节中加以说明;ni为第i个部件被击中的破片数。
用同样的方法计算目标其他部件的毁伤概率,目标总体毁伤概率可表征为
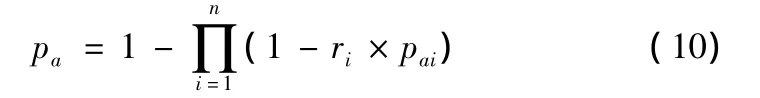
式中:pa为目标整体毁伤概率;n为目标所含部件数;ri为该部件毁伤贡献系数,为描述部件毁伤在整体毁伤中所占权重,为无量纲常数。
3 交汇计算
分析破片与目标在空间交会,需考虑空间位置关系,因为破片飞行线路以及目标交汇比较复杂,在同一坐标系下建立模型计算比较困难;因此,根据需要,建立弹体坐标系、地面坐标系、目标坐标系,由于装甲目标速度相对于破片飞行速度很低,可视装甲目标为静止,将地面坐标系和目标坐标系合并,并确立坐标系之间的转换关系[3]。
3.1 弹体坐标系
战斗部中心为原点Of,OfXf沿战斗部中心轴,以弹头方向为正,OfYf为轴向剖面向上,OfZf为径向剖面垂直 OfYf轴,符合右手法则(如图2所示)。
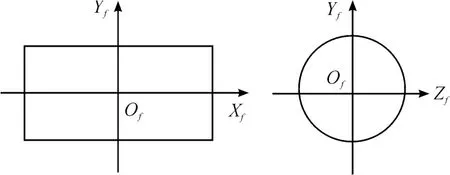
图2 弹体坐标系
3.2 目标坐标系
设装甲目标俯视面几何中心为原点Ot,以车顶平面为xtotzt平面,车长为xt轴,车头方向为正,宽为yt轴,与xt轴呈逆时针90°,zt轴垂直于平面向上(如图3所示)。
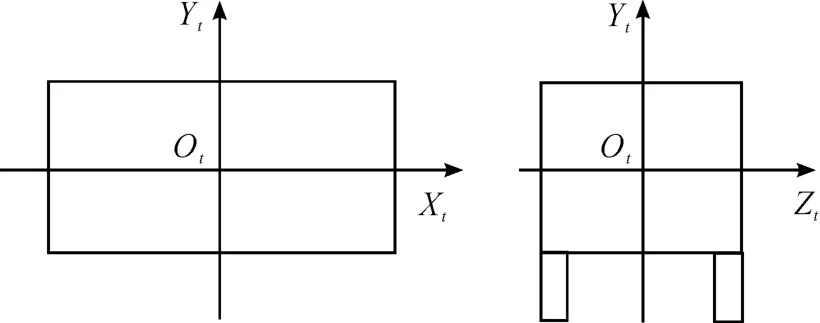
图3 目标坐标系
3.3 坐标系转换
战斗部爆炸时,弹体坐标原点Of在目标坐标系的坐标为(xt1,yt1,zt1),战斗部 xfOfyf平面与目标坐标系 0tytzt平面夹角θ1,弹轴Ofxf与目标坐标系Otxtyt平面夹角为θ2。则两个坐标系之间变换关系为
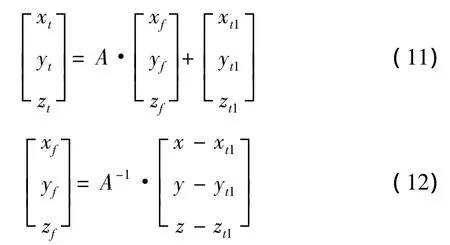
式中A为转换矩阵
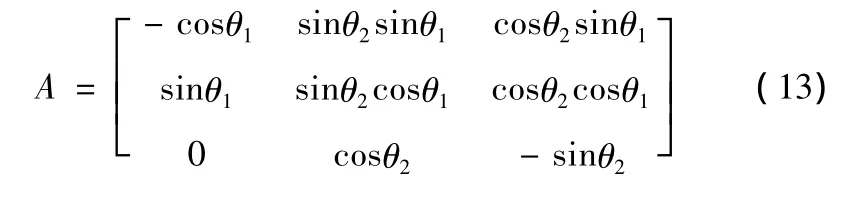
4 毁伤计算
4.1 破片运动轨迹
采用微元法分析破片命中情况,在轴向和径向飞散角内将破片场划分为许多微元,微元划分足够小,则可以认为微元内破片均匀分布,速度相同且方向均为微元中心线方向,根据破片飞散角及弹目相对位置关系,计算出破片与目标交汇的数量,位置和角度等。
由于战斗部为回转体,忽略重力影响,可认为破片在周向上均匀分布,不存在飞散现象,即战斗部爆炸时,破片在垂直弹轴横切面域上为直线运动,方向为战斗部弹轴指向球心,则在弹体坐标系下,破片初始位置 Of0为(xf0,yf0,zfo),周向夹角ψ0为

式中,D为破片球心到弹轴距离。
破片速度方向为
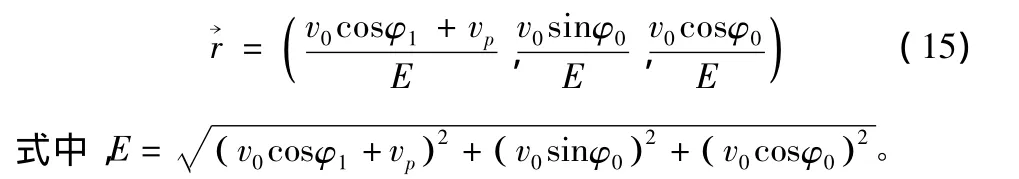
破片运动轨迹可看作起点为Of0,方向为→r的射线,运动轨迹用F(Ofo)表示。
4.2 破片与目标交汇
在目标坐标系上建立毁伤目标的空间几何模型W(x,y,z),通过式(11)将其转换到弹体坐标系中可得
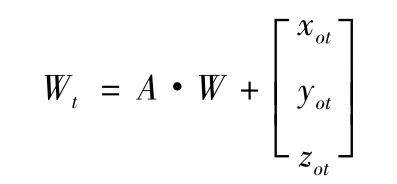
式中,A为转换方程矩阵。
建立弹目交汇方程
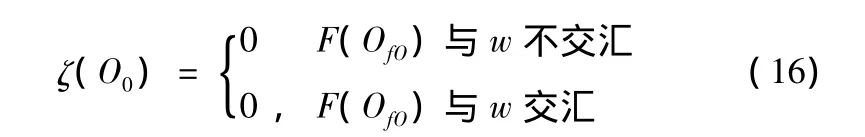
设置N个微元,在轴向上角度为 ψ1、ψ2,周向角度为 ξ1、ξ2,包含n个破片,则微元内破片飞散角可认为都是(ψ1+ψ2)/2,微元内与目标交汇破片数M为
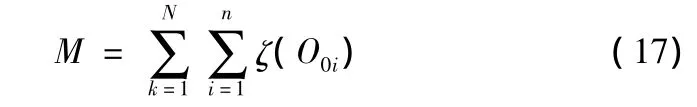
4.3 破片毁伤效能
单个破片对部件毁伤概率可表示为[4]
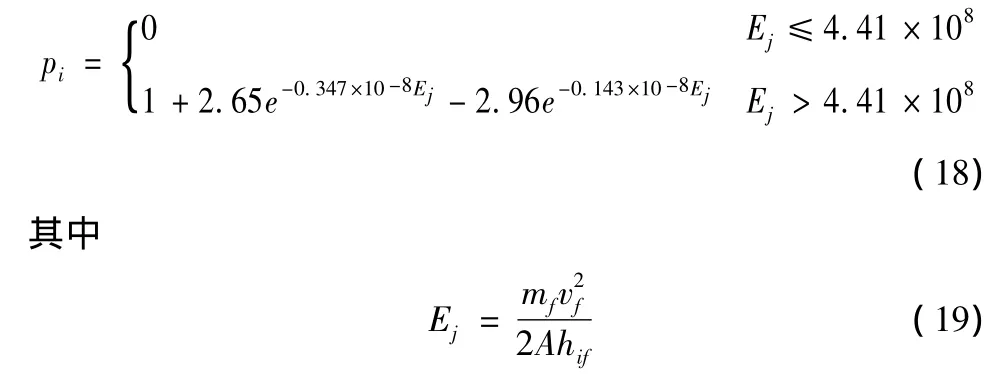
式中:Ej是破片比动能;mf为破片质量;vf是破片速度;hij是部件等效铝板厚度;A为破片迎风面积。
通过计算得出破片交汇数及单枚破片队部件毁伤概率,结合毁伤函数可得出破片场对整个目标的毁伤概率。
5 结论
1)以某型152预制破片弹毁伤某装甲运输车为例,战斗部在车顶中心上方4 m处起爆,速度为350 m/s,落角为30°。计算出对发动机、油箱、人员毁伤概率分别是0.16、0.28、0.44。目标 M、K 级毁伤概率分别为0.4、0.07。
2)研究了预制破片的速度特性和分布规律,从弹目交汇和毁伤概率角度计算毁伤效能,建立破片毁伤计算模型。在此基础上可进一步分析不同起爆点毁伤效能以及弹群对装甲集群目标的毁伤效能。
[1] 张媛.杀爆战斗部对武装直升机的毁伤研究[D].南京:南京理工大学,2012.
[2] 李向东.目标易损性[M].北京:北京理工大学出版社,2013.
[3] 孔祥韶,吴卫国.圆柱形战斗部破片速度及等效装药特性研究[J].振动与冲击,2013(9):146-149.
[4] 张国伟.终点效应及其应用技术[M].北京:国防工业出版社,2006.
(责任编辑杨继森)

