超音速导弹弹翼结构的气动热弹性分析
刘立刚,周 凌,孙 辉
(中国科学院长春光学精密机械与物理研究所,长春 130033)
随着有翼导弹的飞行速度越来越高,尤其是在超音速下进行机动飞行的有翼导弹,气动加热引起的高温将导致弹翼结构部件内产生不均匀的热应力和热变形等现象,继而导致飞行器气动外形、结构强度及结构刚度的变化,影响导弹的飞行性能和战斗性能,有时甚至能导致结构破坏[1,2],这在工程实际中是经常遇到的,所以超音速导弹弹翼这类飞行器的典型结构的气动热弹性分析是一个非常重要的问题。
李建林等给出了复杂外形高超声速飞行器气动热的快速工程估算方法[3]。杨恺等发展了一套高超声速飞行器关键部位气动热的计算方法[4,5]。赵晓利对圆柱壳高超声速气动加热风洞实验进行了三维非定常数值模拟,实验结果验证了耦合计算方法的准确性[6]。李国曙等建立了考虑热效应影响的高超声速飞行器从气动热计算到静气动弹性分析的快速分析方法[7]。杨超等建立了气动热、气动弹性双向耦合高超声速二维曲面壁板颤振分析方法[8]。
本文给出了低、中超音速导弹弹翼结构的气动热弹性分析流程,并给出Ma=5时气动加热引起的弹翼结构的温度场、热应力场、热应变场和热位移场的仿真结果。
1超音速弹翼表面气动加热工程计算
在计算弹翼表面气动加热分布时,将其分为高速可压层流区、高速可压紊流区与弹翼前缘3个区域分别计算,由式(1)先确定弹翼蒙皮变量的层流与紊流区的转捩点坐标xtri

式(1)中:ρ为空气密度;u为气流速度;μ为空气动力黏度;Retri为转捩点处的雷诺数,下标带e为边界层外缘值。对于光滑壁,工程上考虑马赫数影响的转捩准则计算,Retri表达式为

式(2)中,Ma为马赫数。
1.1 层流区、紊流区气动加热计算
将弹翼结构简化成平板,由平板的热流密度公式和Eckert参考温度法,可以得到高速可压层流的平板气动加热公式为[9]

式(3)中:q为热流密度;Pr为普朗特数,这里取为0.7;ρ为空气密度;u为气流速度;μ为空气动力黏度;Rex为当地雷诺数为空气定压比热容;Taw为恢复温度;Tw为弹翼表面壁温;下标带e为边界层外缘值,式中 μ*,ρ*,的工程计算方法如下:

R=287.1(J˙K-1˙kg-1)为单位气体常数,w=0.76。
同样可得高速可压紊流的平板加热公式为[10]

在高温边界层中,传热的基本形式有4种:导热、对流传热、扩散传热和辐射传热。这里只考虑边界层对流传热和弹翼表面辐射传热两种方式。弹翼表面向外辐射的热流量q1表达式为

式(6)中:ε 称为表面黑度因数;σ =5.67 ×10-8W˙m-2˙ K-4,是斯蒂芬—波尔兹曼常数。
高温边界层对弹翼表面加热的热流密度为q,在考虑定常、无内壁冷却情况的热流量平衡方程为

在层流状态下,q为式(3),将其代入式(7),可以得到弹翼表面壁温公式

在紊流状态下,q为式(5),代入到式(7),同样可以得到弹翼表面壁温公式
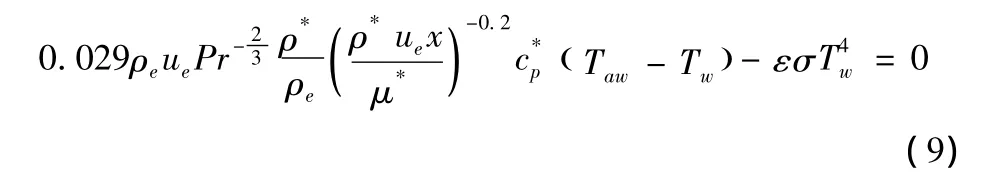
1.2 弹翼前缘气动加热计算
若不考虑弹体对弹翼的影响,弹翼前缘的热流密度可近似按后掠圆柱前缘的热流公式进行计算,并代入到热流量平衡方程式(7)得
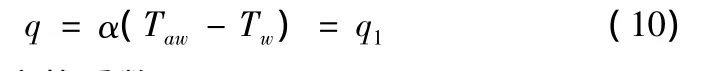
式(10)中,α为热交换系数
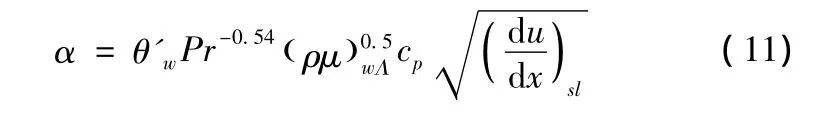
式(11)中,Λ为弹翼后掠角,下标sl为前缘线上的值。θ'w的数值计算关联式为

式(12)中,T∞o和Tno分别为来流总温和垂直于翼前缘方向的动能转化为热能相应的总温

式(15)中,Man∞为来流马赫数在前缘的法向分量;ρno为气体密度;R0为翼前缘半径。PwslΛ为相应于Man∞的正激波后总压,表达式如下:

2 热弹性分析的有限元法
在求得超音速导弹弹翼表面的温度分布之后,将其作为弹翼结构温度场的边界条件,采用有限元法计算弹翼结构的温度场以及热应力场、热应变场和热位移场。
2.1 稳态温度场有限元法
将求解域分为有限个单元,设单元结点为 i,j,m,…,p,结点温度为 Ti,Tj,Tm,…,Tp,单元内任一点温度 Te(x,y,z)用结点温度表示为
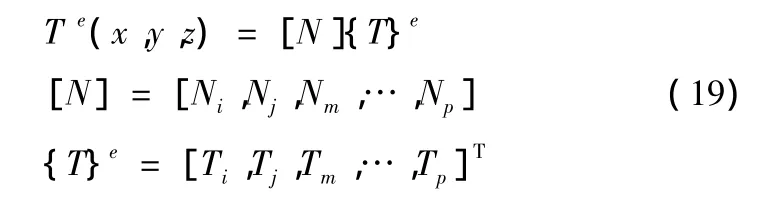
式(19)中,[N]为形函数矩阵,是坐标 x,y,z的函数,{T}e为结点温度矩阵。根据变分原理,对于第一类边界条件,泛函I(T)取得极小值,即对于求解域的全部结点,得到

式(20)中,{T}=[T1,T2,T3,…,Tn]T为包含全部结点的结点温度矩阵,[H]为热传导矩阵。另在第一类边界上的结点温度为已知边界温度,在此条件下求解方程组式(20),即可得到全部结点温度,各单元内部任一点温度可由式(19)插值求得。
2.2 热应力场、热应变场和热位移场有限元法
引起热应力的根本原因是在约束作用下且有温度的变化。用位移法分析结构热应力,应先按温度场的改变计算热变形,进而计算热应力。一个三维弹翼受热有温度变化会发生形状变化,空间内各点都有一定位移,温度变化引起的位移求解方程:

式(21)中,[K]为结构总刚度矩阵;RΔT为全部单元热载荷的迭加,是结构由于受热膨胀而引起的等效为结点的载荷列阵,{δ}为总结点位移。热应变可由下式得到[11]:

进而得到热应力的表达式为
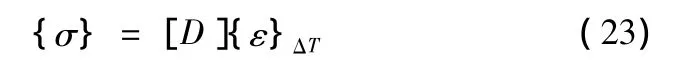
式(23)中,[D]为空间问题的弹性系数矩阵。
3 气动热弹性分析的流程
将气动加热工程计算与有限元法相结合,图1给出弹翼气动热弹性计算流程。

图1 弹翼气动热弹性计算流程
4 气动热弹性分析工程算例
弹翼翼面结构为夹层结构翼面,其外形与有限元网格模型如图2所示。弹翼表面采用蜂窝夹芯蒙皮,内部由3根翼肋与前墙、后墙组成,与弹身的连接是由翼根处前墙和后墙截面上的接头进行连接[12]。其飞行状态和大气物理参数如表1所示。

图2 弹翼结构及有限元网格
弹翼主要由两种材料制造而成,表面蒙皮采用的是蜂窝夹层板材料,内部骨架结构的材料牌号为HasteloyX,是一种轻质合金。它们的物理参数和热性能参数分别见表2和表3。

表1 飞行状态和大气物理参数

表2 材料物理参数

表3 弹性模量和热参数与温度的关系
4.1 弹翼表面气动加热计算
在进行气动加热估算时,弹翼前缘为x坐标原点。当Ma=3时,由式(1)、式(2)计算得到转捩点xtri=0.04 m。
4.1.1 弹翼前缘气动加热计算
由式(7)及式(10)~式(18)可得方程

对式(24)进行求解,可得Tw=889.576 K。
4.1.2 层流弹翼表面壁温计算
层流区为0 <x≤0.04,由式(8)、式(14)可得方程:

计算得到Tw沿x的变化如图3所示,其中0<x≤0.04。

图3 Ma=3时层流Tw变化曲线
4.1.3 紊流弹翼表面壁温计算
紊流区为 0.04 <x≤0.605,由式(9)、式(14)可得方程:
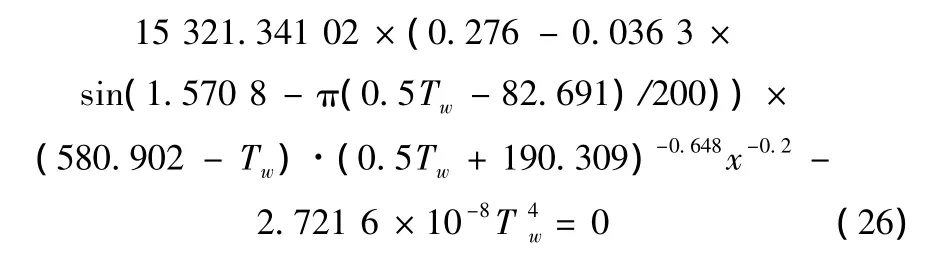
计算得到Tw沿x的变化如图4所示,其中0.04<x≤0.605。

图4 Ma=3时紊流Tw变化曲线
4.2 弹翼结构的温度场
在仿真计算弹翼结构温度场时,将4.1节由气动加热工程估算公式计算得到的弹翼表面蒙皮的气动热分布作为外壁边界条件,弹翼结构内壁的边界条件是空气对流边界条件,空气对流换热系数为 12.5 w˙m-2˙°C-1,空气的初始温度为25℃。图5是计算得到的弹翼结构温度场分布云图。图6~图10给出了蒙皮沿弦向、厚度方向、翼肋沿弦向、前墙与后墙沿展向温度分布。
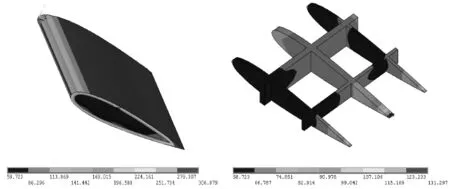
图5 弹翼结构及内部骨架温度分布
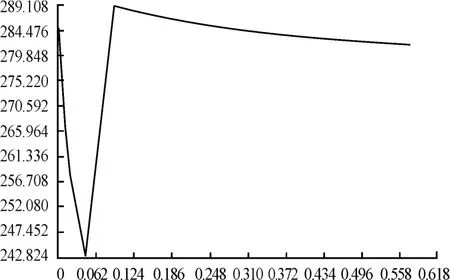
图6 蒙皮弦向温度分布

图7 蒙皮厚度方向温度分布

图8 翼肋弦向温度分布

图9 前墙展向温度分布

图10 后墙展向温度分布
从以上的温度场分布图可以看出:弹翼结构最高温度为289.108℃,是蒙皮表面所加载的最高温度,出现在层流与紊流的转捩点处。沿蒙皮厚度方向,温度呈梯度分布,从外壁到内壁递减变化。沿弦长方向,翼肋在靠近前缘、后缘附近的部分温度较高,中间的翼肋温度较低;前墙、后墙在翼根部温度较低,翼梢处温度较高。
4.3 弹翼结构的热弹性分析
将温度场的结点温度当作温度载荷施加在应力场分析中。并且对于在翼根与弹身连接处的约束作如下处理,将约束加在翼根处前墙和后墙截面上与上下蒙皮截面连接的结点上,图11~图22分别是热应力场、热应变场和热位移场分布云图与变化趋势图。

图11 弹翼结构热应力(Mises应力)及内部骨架结构Mises应力云图
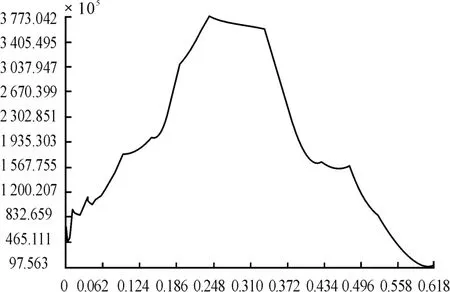
图12 蒙皮沿弦向热应力(Mises应力)变化曲线
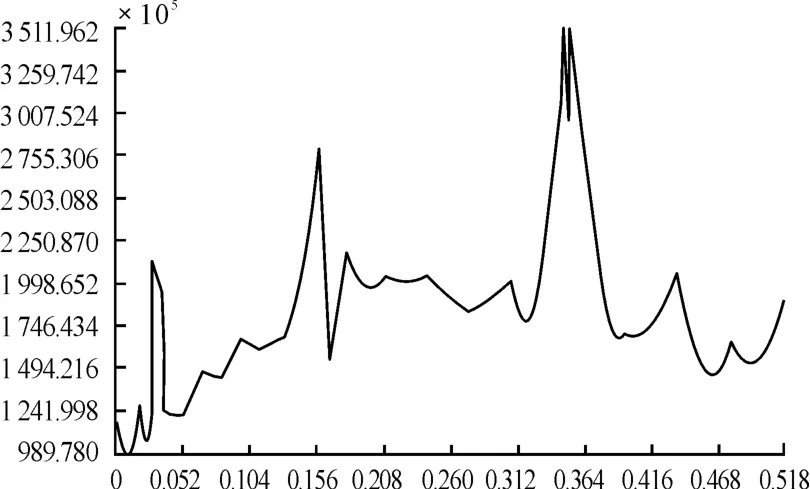
图13 翼肋沿弦向热应力(Mises应力)变化曲线
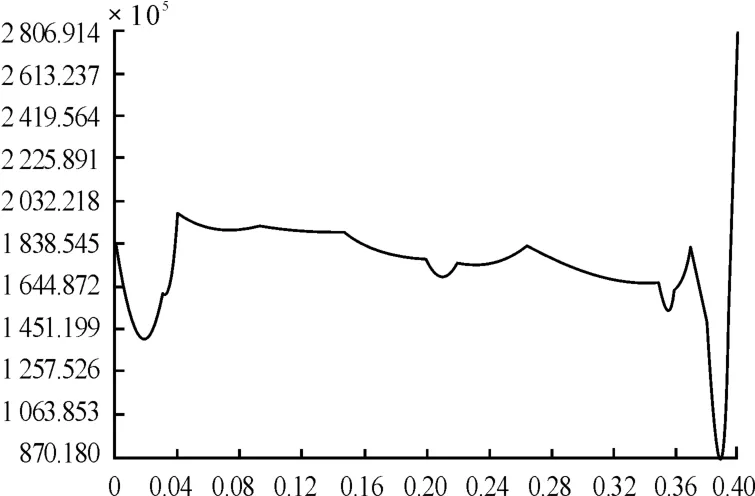
图14 前墙沿展向热应力(Mises应力)变化曲线

图15 后墙沿展向热应力(Mises应力)变化曲线

图16 弹翼结构热应变(Mises应变)及内部骨架结构Mises应变云图

图17 蒙皮沿弦向热应变(Mises应变)变化曲线

图18 翼肋沿弦向热应变(Mises应变)变化曲线

图19 前墙沿展向热应变(Mises应变)变化曲线

图20 后墙沿展向热应变(Mises应变)变化曲线

图21 弹翼结构热位移及内部骨架结构合位移云图

图22 蒙皮沿弦向热位移变化曲线
从弹翼结构的热应力场、热应变场和热位移场分布与趋势图可以得出以下结论:热应力最大值为7.93×108Pa,出现在弹翼与弹身的连接处;沿弦长方向,蒙皮表面前缘、后缘的热应力较小,靠近连接处的热应力较大。由于温度载荷的对称性,在蒙皮表面的应力场也是上下对称的。翼肋沿弦向热应力中间较大,两端较小。前墙热应力沿展向翼梢较大,后墙沿展向热应力翼根与翼梢较大,中间较小。热应变与热应力分布基本一致,最大值为4.367×10-3。最大热位移出现在翼梢的尾部,其值为8.52×10-4m;从计算结果来看,最大热应力、最大热应变、最大热位移均在许可值范围内,可见该弹翼的材料及结构满足设计要求。
5 结论
从算例分析结果得到以下结论:最高温度出现在层流与紊流的转捩点处,其值为289.108℃;最大热应力和热应变均出现在弹翼与弹身的连接处。最大热应力值为7.93×108Pa,最大热应变值为4.367×10-3,可见热应力数值是非常大的,所以对于高超声速飞行的导弹弹翼进行热应力校核是完全必要的;最大热位移出现在翼梢的尾部,其值为8.52×10-4m;最大热应力、最大热应变、最大热位移均在许可值范围内,可见该弹翼的材料及结构满足设计要求。
[1] 姜贵庆,刘连元.高速气流传热与烧蚀热防护[M].北京:国防工业出版社,2003.
[2] 刘芹.弹体结构热振动分析[D].西安:西北工业大学,2004.
[3] 李建林,唐乾刚,霍霖,等.复杂外形高超声速飞行器气动热快速工程估算[J].国防科技大学学报,2012,34(6):89-93.
[4] 杨恺,高效伟.高超声速飞行器关键部位气动热计算[J].计算力学学报,2012,29(1):13 -18.
[5] 赵晓利,孙振旭,安亦然,等.高超声速气动热的耦合计算方法研究[J].科学技术与工程,2010,10(22):5450-5455.
[6] 李国曙,万志强,杨 超.高超声速翼面气动热与静气动弹性综合分析[J].北京航空航天大学学报,2012,38(1):53-58.
[7] 杨超,李国曙,万志强.气动热-气动弹性双向耦合的高超声速曲面壁板颤振分析方法[J].中国科学:技术科学,2012,42(4):369 -377.
[8] 杨 恺,高效伟.高超声速气动热环境工程算法[J].导弹与航天运载技术,2010(4):19-23.
[9] 钱翼稷.空气动力学[M].北京:北京航空航天大学出版社,2004.
[10]中国人民解放军总装备部军事训练教材编辑工作委员会.高超声速气动热和热防护[M].北京:国防工业出版社,2003.
[11]朱加铭,欧贵宝,何蕴增.有限元与边界元法[M].哈尔滨:哈尔滨工程大学出版社,2002.
[12]郦正能.飞行器结构学[M].北京:北京航空航天大学出版社,2005.
(责任编辑周江川)

