涡发生器对风力机翼型绕流场的影响研究

胡　昊， 李新凯

(1.华北水利水电大学 电力学院，河南 郑州450045；

2.华北电力大学 电站设备状态检测与控制教育部重点实验室，北京102206)



涡发生器对风力机翼型绕流场的影响研究

胡昊1,2， 李新凯2

(1.华北水利水电大学 电力学院，河南 郑州450045；

2.华北电力大学 电站设备状态检测与控制教育部重点实验室，北京102206)

摘要：为了研究涡发生器对风力机专用翼型气动性能的影响，采用数值模拟的方法对带涡发生器风力机的翼型进行了数值计算.首先对具有试验数据的带涡发生器翼型进行了数值计算，验证了计算方法的可行性；然后采用该计算设置对所要研究的风力机翼型在多个攻角下的情况进行了计算.结果表明：在小攻角下当翼型未发生流动分离时，涡发生器可能使翼型升阻比降低；当攻角增大，翼型发生流动分离时，涡发生器可以有效推迟流动分离，增大失速攻角，提高升阻比.

关键词：涡发生器；风力机；翼型；绕流场

随着人类对清洁能源的迫切需求，风力发电、水力发电[1]及光伏发电[2]正逐步成为新能源中的主要组成部分.随着风力机的大型化发展，叶片长度越来越长，为满足强度要求，叶片根部往往采用大厚度翼型，由于叶根扭角的限制，其翼型的实际工作攻角偏大.在运行工况下，风力机叶片根部会发生较大的流动分离，若叶片发生流动分离将严重影响风力机风轮对风能的捕获功率.所以抑制叶根处流动分离是提高风力机气动功率的有效手段.

涡发生器(Vortex Generators，VGs)属于被动流动控制，能有效抑制边界层的流动分离[3-5].涡发生器通过产生近似的流向涡将边界层外的高能流体卷入边界层底层从而达到抑制边界层分离的目的，是流动控制中的研究热点[6-10].Bons等[6-7]于1999—2001年研究了在涡轮叶片表面应用小孔稳态射流和脉冲射流进行流动控制，研究结果表明，流动控制能够有效地控制叶片表面边界层的分离流动.国内清华大学金琰和袁新[11]通过数值模拟的方法研究了在翼型背部加入射流从而达到减小翼型颤振的目的.

目前，研究VGs对风力机专用翼型绕流场影响的成果还较少.因此，研究涡发生器对翼型绕流特性的影响，为改进风力机的流动控制提供依据，此研究具有重要的实际意义.文中采用数值模拟的方法，研究了三角形涡发生器对风力机专用翼型气动特性的影响.

1模拟计算

1.1　几何模型

文中的翼型为风力机专用翼型，相对厚度21%，计算模型弦长0.6 m，展长0.25c(c为模型弦长，m)，如图1所示.计算验证模型的相对厚度30%，计算模型弦长0.6 m，展长0.25c，如图2所示.涡发生器几何参数及排列方式如图3所示，展向布置4对VGs，安装于距前缘0.2c处.

图1　计算模型

图2　计算验证模型

图3　VGs几何参数(单位:mm)

1.2　计算方法

采用商业软件Fluent进行数值模拟计算.用压力求解器求解，算法为SIMPLE.湍流模型为全湍流SST模型.

计算域：由于VGs的排列方式在展向上具有周期性，翼型段两侧对称，展向计算域尺度为翼型段长度.在翼型段前后和上下分别延伸了20c，30c，20c，20c.

计算网格：采用商业软件ICEM进行全域结构网格划分，网格总数220万.在涡发生器周围进行网格局部加密，结果如图4所示，其中h为VGs高度.

图4　边界条件及网格分布

2计算结果分析

2.1　计算验证模型

为了验证数值计算方法的可靠性，首先对荷兰Delf大学风能研究中心完成的DU97-W-300翼型和三角翼VGs试验模型进行CFD模拟.来流风速为48.7 m/s，基于弦长的雷诺数为2×106.图5给出了数值计算的升力系数与试验值.为了观察VGs的作用，图中还给出了光滑翼型升力系数的试验数据和计算结果.

图5　验证模型的模拟计算结果

从图5中可以看出：无论是否有VGs，在所研究的攻角范围内，数值计算得到的升力系数均与试验值吻合较好，表明所采用的计算方法满足本研究的精度要求；装有VGs的翼型推迟了流动分离，使失速攻角增大，在10°～15°攻角范围内翼型的升力得到了大幅提高.

2.2　计算结果分析

采用上述所用的数值方法对相对厚度21%的风力机专用翼型进行数值计算.

2.2.1有、无VGs翼型的升、阻力系数情况

图6为该翼型有、无VGs控制时翼型的升、阻力系数计算结果.

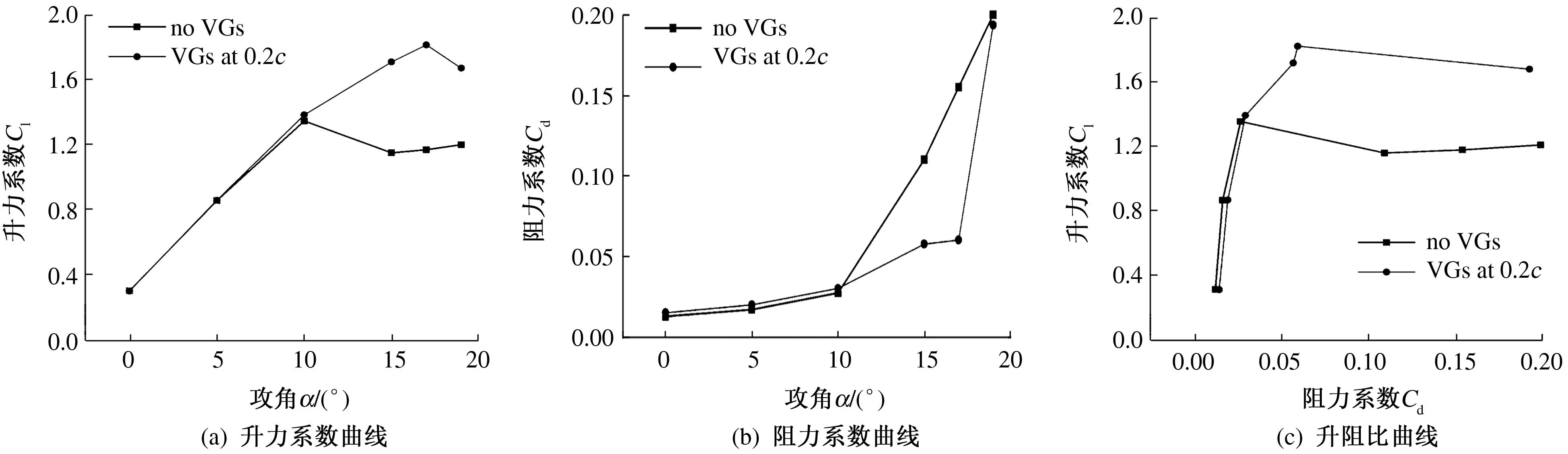
图6　不同攻角下翼型的升、阻力系数及升阻比

从图6中可以看出：安装VGs的翼型，其失速攻角增加了7°左右；当攻角α=0°和5°时，带VGs翼型的升力系数变化不大，阻力系数增加较多，升阻比下降；当α=10°时，虽然升力系数有所增加，但阻力系数也增加了，升阻比下降；当α=15°和17°时，升力增加，阻力减小，升阻比增加较为明显；当α=19°时，有、无VGs情况下阻力系数相差不多，升阻比增加.

2.2.2有、无VGs翼型的压力系数情况

取图7所示的翼型中间位置为研究对象，研究压力系数的变化.图8为翼型中间截面处的压力系数分布曲线.从图8中可以看出：在α=15°和17°两个攻角下，发生了较大的流动分离，在翼型吸力面出现了较大的压力平台，而带VGs翼型吸力面压力恢复较好，压力平台变小，推迟了流动分离；在α=19°攻角下，有、无VGs翼型时的压力系数均出现了较大的流动分离.

图7　翼型中间位置示意

图8　在不同攻角下翼型的中间截面压力系数

2.2.3旋涡的判别和变化规律

涡量定义为，流场中任何一点微团角速度的2倍.所以在壁面上由于流体速度的应变率很大，造成靠近壁面附近的涡量值很大，很明显，这不是要研究的旋涡产生的涡量值.而旋涡的强度(涡通量)则是指涡量在一个截面上的积分.在一平面中，涡通量为

由于VGs处于壁面上，旋涡向下游发展时随着涡核半径的不断增大，靠近壁面的侧旋涡的发展会受到抑制，2个旋涡之间也会有干涉，旋涡的涡核形状不规则，造成涡核包围的面积A不容易获得.为此需要给出一个客观分辨涡旋的判据.这样的判据在伽利略变换中是不变的，它不依赖于坐标的选择和旋转等变换，能分辨出涡轴的位置和方向等.目前在文献中普遍采用的是Q判据，

(1)

式中eij，Ωij分别为应变速率张量和涡量张量.文中采用Q判据来显示旋涡结构.

图9为带VGs翼型在不同攻角下和不同翼型弦向位置处的涡量等值云图；图10为带VGs翼型在不同攻角下的Q等值云图.从图9和图10中可以看出旋涡沿流向的变化规律，在15°，17°，19°攻角下，旋涡耗散得较快.

图9　不同攻角α下的涡量云图

图10　不同攻角α下的Q等值面图

Hunt等提出把Q>0的区域定义成涡，类似于涡通量，将Q在一个截面上的积分定义为Q通量来表示旋涡强度.在平面中，对于Q通量，有

这样就可以避免在壁面附近出现涡量很大的问题.

以VGs中某一个小翼产生的旋涡为研究对象，在VGs下游不同弦向位置处将Q值在其所包围的面积上进行积分得到Q通量，如图11所示.从图11中可以看出，旋涡距前缘0.5c位置处的旋涡强度已经很低，总体上旋涡强度基本呈指数规律耗散.

图11　Q通量随流向距离C的变化规律

3结语

通过对射流式涡发生器进行数值模拟，得出以下主要结论.

1)从有、无涡发生器控制下翼型的升、阻力系数来看，当翼型未发生流动分离时，VGs可能使翼型的升阻比降低.当翼型发生较小的流动分离时，VGs可以有效推迟流动分离，增大失速攻角，提高升阻比.

2)根据涡通量公式，定义了Q通量来判别集中涡的强度.对比不同攻角下涡通量随流向的耗散可以发现，总体上旋涡强度与流向距离的变化趋势基本呈指数规律耗散.

参考文献

[1]吴泽鑫,刘琛,安周，等．基于分布式水文模型的流域输沙过程模拟[J]．华北水利水电大学学报(自然科学版)，2014，35(5)：1-4．

[2]吴志超,孟现岭,赵地，等．光伏发电中基于拉格朗日插值法的最大功率点跟踪[J]．华北水利水电大学学报(自然科学版)，2014，35(5)：78-80．

[3]Lin J C.Review of research on low-profile vortex generators to control boundary-layer separation[J].Progress in Aerospace Sciences,2002,38(4-5):389-420.

[4]Johansen J,Soerensen N N,Zahle F,et al.Aerodynamic Accessories[R].Denmark:Risoe National Laboratory，2004:Risoe-R-1482.

[5]Johansen J,Soerensen N N,Peck M,et al.Rotor Blade Computations with 3D Vortex Generators[R].Denmark:Risoe National Laboratory,2005:Risoe-R-1486.

[6]Sondergaard R,Bons J P,Rivir R B.Control of low-pressure turbine separation using vortex generator jets[J].Journal of Propulsion and Power,2002,18(4):1047-1054.

[7]Bons J P,Sondergaard R,Rivir R B.Turbine separation control using pulsed vortex generator jets[J].Journal of Turbomachinery-Transactions of the ASME,2001,123(2):198-206.

[8]Posfl D,Gross A,Fasel H F.Numerical investigation of active flow control for low-pressure turbine blade separation[J/DB].AIAA Paper,2004:0738-0750.

[9]Gross A,Fasel H F.Simulation of active flow control for a low pressure turbine blade cascade[J/DB].AIAA Paper,2005:2005-869.

[10]Rizzetta Donald P,Visbal Miguel R.Numerical study of active flow control for a transitional highly-loaded low-pressure turbine[J/DB].AIAA Paper,2005:2005-5020.

[11]金琰,袁新．风力机翼型颤振及射流减振技术的气动弹性研究[J]．太阳能学报，2002，23(4)：403-407．

(责任编辑: 杜明侠)

Effect of Vortex Generators on the Flow Fields around the Airfoil of Wind Turbine

HU Hao1,2， LI Xinkai2

(1.School of Electric Power, North China University of Water Resources and Electric Power, Zhengzhou 450045, China;

2.Key Laboratory of CMCPPE of Ministry of Education, North China Electric Power University, Beijing 102206, China)

Abstract:In order to study the influences of vortex generators on the aerodynamic performances of the airfoil of wind turbine, the numerical simulation method was adopted to calculate the airfoil of wind turbine with vortex generators. Firstly, the airfoil with vortex generators with experimental data was simulated and calculated, the computing method was feasible by testing. Then adopting the computing sets, the airfoil of wind turbine was calculated under multiple attack angles. The computing results show that vortex generators make the lift-drag ratio of airfoil decrease when the airfoil does not occur flow separation under little attack angles, and when the airfoil occurs flow separation under big attack angles, the vortex generators can effectively delay the flow separation, increase the stall angles and the lift-drag ratio.

Keywords:vortex generators；wind turbine；airfoil；flow field

中图分类号：TK83

文献标识码：A

文章编号：1002-5634(2015)02-0058-05

DOI:10.3969/j.issn.1002-5634.2015.02.013

作者简介：胡昊(1979—),男，河南南阳人，讲师，博士研究生，主要从事风力机气动分析及流体机械方面的研究.李新凯(1984—),男，河北保定人，讲师，博士研究生，主要从事风力机气动分析及流动控制方面的研究.

基金项目:河南省重点科技攻关计划项目(142102210059).

收稿日期:2014-11-19