因果强度推理的贝叶斯模型综述*
因果强度推理的贝叶斯模型综述*
刘雁伶1,黄仁辉2,胡竹菁3
(1.江西科技师范大学教育学院,南昌 330013;2.宜春学院心理教育中心,宜春 336000;
3.江西师范大学心理学院,江西省心理与认知科学重点实验室,南昌 330022)
摘要:因果强度推理的贝叶斯模型以因果协变关系、贝叶斯定理和因果图形模型为基础,借助蒙特卡洛算法实现模型对被试因果强度估计的预测。通过选用不同的先验分布、似然函数、蒙特卡洛取样方法和基于后验分布的预测方法,因果强度推理的贝叶斯模型可以精确预测很多以往模型不能解释的实验结果,并对被试的推理过程提出有价值的见解,还可推广到对因果结构判断的预测和对多原因(结果)交互作用的解释;但需要在如何选择先验分布和似然函数、解释被试如何表征与作答、扩大单个模型解释范围和简化计算等方面继续完善。
关键词:因果强度推理;贝叶斯模型;先验分布;综述
因果推理的贝叶斯模型是认知计算心理物理学方法在因果推理领域的实践(Lu,Yuille,Liljeholm,Cheng,& Holyoak,2008),是贝叶斯推断统计与因果推理理论相结合获得的先进的研究成果。贝叶斯推断统计是与经典推断统计同时诞生但直到近100年才逐步发展起来的推断统计方法,它与经典推断统计最重要的区别就在于经典推断统计将总体参数视为一个未知的常数,使用样本统计量去估计它,而贝叶斯推断统计将总体参数视为随机变量,使用先验分布来约束它(韦来生,2008)。正是先验分布的使用使得贝叶斯推断统计可以在少数几个观测值的基础上得出合理有效的结论,而不必像经典推断统计那样必须以大量的观测数据为基础。因果推理往往就是必须在少数几个观测值的基础上得出有效结论的认知过程,因果推理的贝叶斯模型通过引入合适的先验分布实现了在少数几个观测值基础上的归纳和概括(Griffiths,Kemp,& Tenenbaum,2008),并在因果强度估计和结构判断(Lu et al.,2008;Griffiths & Tenenbaum,2005;Chater,Tenenbaum,& Yuille,2006)、动态因果关系学习(Danks,Griffiths,& Tenenbaum,2003)、干预在因果学习中的作用(Steyvers,Tenenbaum,Wagenmakers,& Blum,2003)等方面取得了突破性的进展。因果推理研究中的结构判断是指被试必须做出判断:所考察的原因是否影响效果出现的概率?强度估计指在确定了因果关系的结构之后对所考察原因的效力的估计,本文就因果强度推理研究领域的贝叶斯模型做一简介。
首先介绍因果强度推理的贝叶斯模型的理论基础,包括因果协变关系、贝叶斯定理、因果图形模型和蒙特卡洛方法四个方面,其中的协变关系是被试推断因果关系的依据,贝叶斯定理是贝叶斯推断统计方法的根本原理,因果图形模型是建立因果推理贝叶斯模型的前提假设,蒙特卡洛方法是贝叶斯模型模拟被试表现时必备的计算工具;其次介绍因果强度推理领域涉及的先验分布和似然函数,先验分布描写了被试已具备的关于因果推理的背景知识,似然函数表示给定条件下得到观测数据的概率,先验分布和似然函数结合得到后验分布,被试的因果推断就是基于后验分布;再次介绍由这些先验分布和似然函数构建的贝叶斯模型及其预测方法,最后对贝叶斯模型的优势、局限和今后的研究方向做一展望。
1理论基础
1.1协变关系
Hume(1777/2007)认为因果关系不能直接观察获得,但可以通过目标原因和结果之间的协变关系(见表1)推断出来。这一观点一直影响着因果推理领域的研究,现有的绝大多数因果推理模型都是基于使用协变关系来探讨因果推理规律的研究成果建立的。

表1 目标原因(C)与效果(E)之间的协变关系
在上述协变关系中,大写字母C表示目标原因,大写字母E表示效果,小写字母a、b、c、d分别表示目标原因出现时效果出现、目标原因出现时效果不出现、目标原因不出现时效果出现、目标原因不出现时效果不出现的频数,目标原因不出现时导致效果出现的原因被统称为背景原因(一般用大写字母B表示)。
1.2贝叶斯定理
贝叶斯模型使用贝叶斯推断统计方法解释和预测人类和动物被试的认知过程。贝叶斯推断统计的核心概念是贝叶斯定理,贝叶斯定理是关于条件概率的逆概率规则(陈希孺,1999),用公式表示为:
(1)
式(1)显示如何从给定H时D出现的条件概率得到给定D时H出现的条件概率。其中的P(H)指H出现的概率,当P(H)是一个常量时被称为先验概率,当它是一个变量时被称为先验分布;P(D|H)指给定H时D出现的概率,当P(D|H)是一个常量时被称为可能性,当它是一个变量时被称为似然函数;P(H|D)指D出现时H出现的概率,当P(H|D)是一个常量时被称为后验概率,当它是一个变量时被称为后验分布。贝叶斯定理可以简单地表述为后验概率(分布)与先验概率(分布)和可能性(似然函数)的乘积成正比。不同的先验分布和似然函数可以组合建构出不同的贝叶斯模型。
1.3因果图形模型
图形模型提供了有效的方法表征先验分布和似然函数之积的多维联合概率分布(Pearl,2000)。因果图形模型建立在有向模型的基础上,以图1所示最简单的因果情境为例:因果图形模型认为背景原因(B)、目标原因(C)和效果(E)三者之间存在以下两种有向图表示的关系:
图1中的圆是一个节点,表示由不同分布函数定义的不同变量,箭头表示变量之间的概率相关性,有向图0表示背景原因可以影响效果出现,有向图1表示背景原因和目标原因都可以影响效果出现;w0表示背景原因的效力,w1表示目标原因的效力,都在[0,1]之内取值。背景原因被假设为一直存在并导致效果,目标原因对效果的影响有三种方式,包括产生式:目标原因的出现增加了效果出现的概率;预防式:目标原因的出现减少了效果出现的概率;无关式:目标原因的出现对效果出现的概率没有影响;产生式、预防式和无关式统称为因果方向。因果图形模型不但能表征变量(如B、C、E)的概率分布,还可以表征干预(如保持B不变,增加原因C1、C2)导致的原因交互的联合概率和效果概率分布的变化。
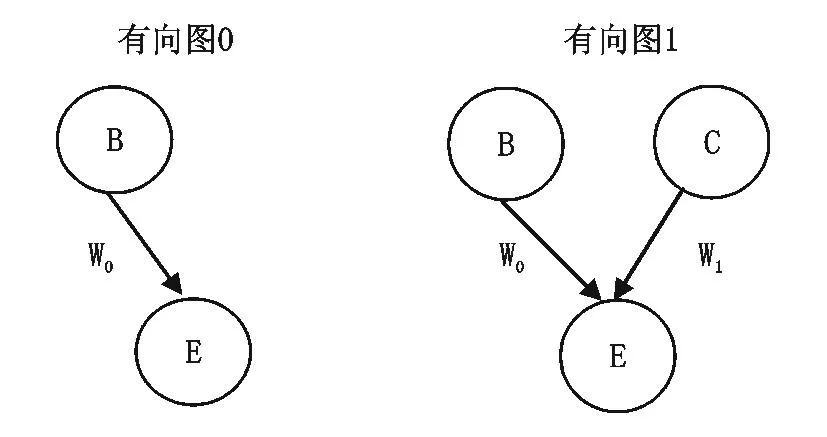
图1 图形模型的两个有向图
1.4蒙特卡洛方法
在使用贝叶斯公式时,没有合适的方法精确计算先验分布和似然函数的多维联合概率分布,蒙特卡洛方法是解决这个问题的一个近似算法。蒙特卡洛方法指从一个分布中获得一系列取样,并用这些取样来表征该分布的方法(韦来生,2008)。在近似计算多维函数的积分时,蒙特卡洛方法从自变量的所有可能取值中取样,并用这些取样计算多维函数的函数值,用获得的函数值的平均数估计多维函数的平均数,当取样数量增加时,估计准确度也增加。
蒙特卡洛方法的一个缺陷是很难做到自动产生合理的取样,解决这个问题的最常使用的方法是马尔科夫链蒙特卡洛方法。马尔科夫链指一个具有马尔科夫性质的随机变量取值过程,马尔科夫性质指随机变量的第n次取值只跟第n-1次取值有关,而与前面和后面的取值无关,变量在前一个取值的基础上取其他值的概率取决于转换核,Metropolis-Hastings算法可以为任意的目标分布建构转换核以保证取样后所得的分布就是目标分布。
2先验分布
因果推理贝叶斯模型所涉及的先验分布主要包括指定先验、均匀先验、SS先验、实验获得先验等。
2.1指定先验分布
指定先验分布指研究者为因果关系的存在概率指定一个数值,或为目标(背景)原因的效力指定一个数值。指定先验分布方法使贝叶斯模型的弹性受很大影响,只能解释某些特定条件下的实验结果,当实验条件(包括因果方向、数据呈现方式、提问方法等)发生变化时需要重新指定先验分布。
2.2均匀先验分布
均匀分布指原因效力w0、w1在其取值范围内取任何值的可能性都是相同的,是一种无信息先验分布。这种无信息先验分布对贝叶斯推断结果的不良影响很小,所以在贝叶斯推断统计研究的初期常被使用,但随着研究的深入均匀分布在解释特定研究领域的特定现象时显示出劣势,因果强度推理领域的研究者开发出包含更大信息量的先验分布来更好地解释被试的背景知识。
2.3SS先验分布
Lu等(2008)认为被试在进行因果关系推断时更倾向于使用有最少(Sparse)的原因同时每个原因有最大(Strong)因果效力的先验分布,他们把这种偏好定义为SS先验,并使用指数函数分别约定产生式和预防式条件下的w0和w1的先验分布。
2.4实验获得先验分布
Yeung和Griffiths(2011)使用被试对协变关系中w0和w1的直接估计来约定w0和w1的先验分布。他们使用重复学习的方式发现被试对w0的最终估计容易受最初呈现的协变关系中的w0的影响,对w1的最终估计很少受最初呈现的协变关系的影响;w0大多数的取值分布在接近0和1的位置,而w1在[0,1]之间取值分布更均匀。
3似然函数
在确定了先验分布后,因果推理贝叶斯模型需要用似然函数解释给定先验分布条件下得到观测数据(即协变关系)的概率。
早期的简化贝叶斯模型(Anderson & Sheu,1995)并未区分产生式与预防式因果方向。使用式(2)描述存在因果关系时得到协变关系数据的概率:
(2)
使用式(3)描述不能确定因果关系时得到协变关系数据的概率:
(3)
式(2)中pC表示目标原因出现时效果出现的概率;pA表示目标原因不出现时效果出现的概率。式(3)中的pN表示效果出现的总概率,式(2)、(3)中的a、b、c、d取自协变关系(除特别说明之外,本文其他位置出现的a、b、c、d均取自协变关系)。
近年的研究(Cheng,1997;Griffiths&Tenenbaum,2005;Luetal.,2008)认为被试在进行产生式因果强度估计时使用式(4)所示的Noisy-OR似然函数,在进行预防式因果强度估计时使用式(5)所示的Noisy-AND-NOT似然函数。
P(e+/b,c;w0,w1)(产生式)=1-(1-w0)b(1-w1)c
(4)
P(e+/b,c;w0,w1)(预防式)=w0(1-w1)c
(5)
式(4)中的e+ 表示效果出现;b和c在{0,1}中取值,当背景(目标)原因出现时b(c)取值为1,否则b(c)取值为0,w0,w1的意义与因果图形模型相同;式(5)各参数的意义与式(4)相同。当w1=0时式(4)、(5)都可以用于描述无关式因果关系,效果的出现完全取决于背景原因。使用Noisy-OR函数和Noisy-AND-NOT函数的一个重要前提是背景原因和目标原因独立影响效果出现的概率,相互之间不存在交互作用。因此产生式因果关系中目标原因的效力指的是目标原因对背景原因未导致效果的部分(协变关系中的d)的影响,预防式因果关系中目标原因的效力指的是目标原因对背景原因导致效果的部分(协变关系中的c)的影响。
4因果强度推理的贝叶斯模型
目前最具代表性的因果强度推理贝叶斯模型包括简化贝叶斯模型、因果支持模型、类属模型和SS模型,以下简单介绍这四个模型。
4.1简化贝叶斯模型
4.1.1先验分布
Anderson和Sheu(1995)提出的简化贝叶斯模型为每一个实验指定一个存在因果关系的先验概率,如在模拟他们的实验一数据时指定存在因果关系的先验概率P(H)=0.40。
4.1.2模型建构
简化贝叶斯模型认为推断是否存在因果关系应该比较协变关系对假设1:存在因果关系的支持度,和对假设0:不能确定是否存在因果关系的支持度:
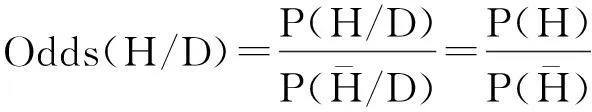
(6)
4.1.3简化贝叶斯模型的强度预测
简化贝叶斯模型使用Odds(H/D)推断因果关系,使用式(7)预测被试的因果强度估计值:
(7)
4.2因果支持模型
4.2.1先验分布
Griffiths和Tenenbaum(2005)提出的因果支持模型假定背景原因和目标原因的效力w0、w1的先验分布是在区间[0,1]内的均匀分布,使用随机取值的方法赋值给w0和w1。
4.2.2模型建构
Griffiths和Tenenbaum(2005)认为即使被要求作出因果强度估计,被试进行的仍然是因果结构的判断。对因果结构的判断通过比较协变关系对有向图1和有向图0的支持度来进行,见式(8):
(8)
其中D表示被试观察到的协变关系数据,对上式两边进行对数运算得到:
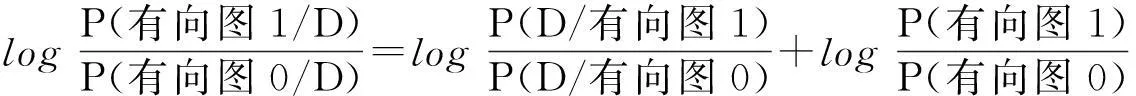
(9)
由于没有证据表明哪个有向图更具可能性,所以P(有向图1)=P(有向图0),使得式(9)右边的第二部分等于0,由此他们指定:

(10)
由于假定背景原因和目标原因的效力取值均为(0,1)上的均匀分布,式(10)的分母可以使用简单的公式求得:
(11)
式(10)的分子部分不能直接求得,但可以使用马尔科夫链蒙特卡洛方法以较高的精度近似计算(计算程序可以在Griffiths教授个人网页上获得)。
4.2.3因果支持模型的强度预测
因果支持模型将因果结构判断的Support值作为模型的因果强度预测值。Support值为正意味着式(10)的分子大于分母,数据D更支持有向图1,被试会认为目标原因与效果之间存在因果关系;Support值为负意味着数据D更支持有向图0,被试会认为目标原因与效果之间不存在因果关系;Support值的绝对值越大意味着它越支持相应的有向图,相应的因果强度预测值也越大。
4.3类属模型
4.3.1先验分布
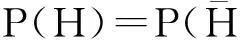
4.3.2模型建构
因果支持模型认为即使被要求作出因果强度估计,被试进行的仍然是因果结构的判断,在此基础上,Griffiths和Tenenbaum(2009)提出一个简单的贝叶斯模型:类属模型。类属模型只计算协变关系数据对有向图1的支持度,以此来模拟被试的因果强度估计。
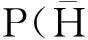
P(有向图1/D)=P(D/有向图1)•P(有向图1)/P(D/有向图1)•P(有向图1)+P(D/有向图0)•P(有向图0)
(12)
4.3.3因果强度估计
以P(有向图1/D)值为因果强度预测值。
4.4SS模型
4.4.1先验分布
Lu等(2008)提出的SS模型采用SS先验作为w0和w1的先验分布。
4.4.2模型建构
SS模型认为目标原因C产生或预防效果E的强度可以用w1的后验概率分布来表示。在获得协变关系D之后,w1的后验概率分布为:
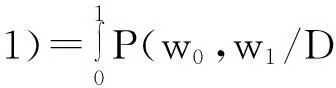
(13)
其中的P(D/w0,w1,有向图1)是似然函数,产生式条件下是Noisy-OR函数,预防式条件下是Noisy-AND-NOT函数;P(w0,w1/有向图1)是w0和w1的先验分布,在SS模型里为SS先验;P(D)是标准化项,表示获得观察到的协变关系的概率。在进行贝叶斯推断统计时,由于标准化项与w1无关,可以将P(D)看做一个常数。
4.4.3SS模型的因果强度预测
SS模型的因果强度预测被定义为求w1后验分布的均值:
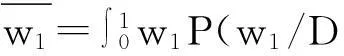
(14)
以上四个模型在先验分布、似然函数、蒙特卡洛算法和预测方法四方面存在差异:先验分布方面简化贝叶斯模型和类属模型都使用指定的先验概率,而因果支持模型和SS模型则分别使用均匀先验和SS先验分布;似然函数方面类属模型、因果支持模型和SS模型均使用Noisy-OR函数和Noisy-AND-NOT函数,简化贝叶斯模型则另外指定的似然函数;蒙特卡洛算法方面因果支持模型和类属模型采用随机抽样,SS模型采用重要性抽样,还有研究使用蒙特卡洛粒子过滤算法(Abbott&Griffiths,2011);预测方法方面简化贝叶斯模型、因果支持模型和类属模型都是因果结构判断的模型,只是使用一些线性转换将因果结构预测值转化为因果强度预测值(简化贝叶斯模型)或直接将因果结构预测值认定为因果强度预测值(因果支持模型和类属模型),只有SS模型专门为因果强度估计构建了参数估计模型。从中可以看出贝叶斯模型的建构方式就是选择不同的先验分布、似然函数、蒙特卡洛算法和预测方法。
5实际应用中的优势
5.1表征了尚未确定的因素对研究对象的影响
通过引入概率分布函数,贝叶斯模型对因果强度的预测不再是一个点估计,而是一个包含各种影响因素,特别是暂时不能确定影响方式和影响力大小的因素在内的后验概率分布(Griffiths,Chater,Kemp,Perfors,&Tenenbaum,2010)。这是推理过程受多方面因素影响这一普遍认知在模型建构中的充分反映,也是对决策理论中“winornothing”原则的有效补充。
5.2融合了自下而上和自上而下的两种方法
先验分布体现了被试已具备的关于因果推断的背景知识,由先验分布驱动的推断是自上而下的推断;似然函数体现了观测得到的数据对因果推断的影响,由数据驱动的推断是自下而上的推断。贝叶斯模型将先验分布与似然函数有机地结合起来,实现了自下而上和自上而下的方法的结合(Tenenbaumetal.,2006;Griffithsetal.,2010)。结合了两种方法的贝叶斯模型可以确定复杂的因果结构,还可以解释被试如何从时空相依的实验情境中作出因果推断,如被试的因果推断如何随观测数据的变化而变化,上一次因果推断形成的后验概率如何变成(或改编成了)下一次因果推断的先验概率。
5.3能得到更精确的预测
因果强度推理模型可以大致分为标准化模型和非标准化模型(Perales&Shanks,2007)。贝叶斯模型属于标准化模型,但其预测能力比其他标准化模型更强,如因果支持模型可以精确预测被试在无关式协变关系上表现出的效果密度效应和原因密度效应,SS模型还可以进一步预测和解释取样大小效应,因果方向上的不对称现象等。建构在集中呈现范式(协变关系中a、b、c、d同时呈现)基础上的贝叶斯模型可以推广到序列呈现范式(a、b、c、d包含的样例随机逐个呈现)的很多研究中,而非标准化模型则更适合于解释序列呈现范式的研究结果;贝叶斯模型还可以应用于多原因或(和)多效果的实验情境,而非标准化模型在这方面存在较大困难。贝叶斯模型另一个重要的优势是可以在稀疏的观测数据基础上得出合理的结论,这是以往的任何模型都很难实现的。
6有待完善的领域
6.1需要有系统的方法确定先验分布和似然函数
先验分布和似然函数的确定直接影响到模型的建构和预测,如果使用错误的先验分布或似然函数,得到的贝叶斯模型可能不适合,模型的预测也就可能与被试的因果强度估计毫无关系,这是贝叶斯模型受到批评最多的地方(Mcclellandetal.,2010;Perforsetal.,2011)。目前有两个方面的理论成果:Noisy-Logical似然函数和等级贝叶斯模型方法可以为解决该问题提供帮助。
Yuille和Lu(2008)提出的Noisy-Logical函数可以帮助研究者确定似然函数,不管是单原因还是多原因因果推理问题都可以从中找到合适的似然函数。但是Noisy-Logical函数将所有原因的交互作用都纳入似然函数使得函数形式臃肿,当目标原因增加时计算上的困难也以几何级数方式增加,所以必须找到合适的途径挑选出效力较大的原因及其交互作用,经典推断统计中的向前向后回归方法和科学理论中的Occam’sRazor原则可以为解决这个问题提供帮助。先验分布方面可以使用等级贝叶斯方法来获得所有层面的知识:获得先验分布、使用先验分布推断数据、估计参数等(Kempetal.,2007),它的基本思想是对不同抽象层次的知识做贝叶斯推断,上一级为下一级规定先验分布,如果该分布足够简单,就直接使用该等级的贝叶斯模型,如果该分布还是很复杂,则逐渐增加贝叶斯模型的等级,直到最高级的背景知识足够简单和概括化,甚至可以认为是生来俱有的。
目前对Noisy-Logical似然函数和等级贝叶斯模型方法的使用还不广泛,后续研究应该使用这些严谨的科学方法来确定先验分布和似然函数,而非仅仅依赖研究者的主观判断。
6.2需要解释被试如何表征问题和作答
Marr(1982)提出了计算解释的三个水平:计算水平(确定问题可以被解决的实质、解决问题时需要用到的信息和问题何以能被解决的逻辑);算法水平(确定解决问题时所需使用各种表征和加工)和执行水平(确定各种表征和加工如何具体得以实施)。贝叶斯方法在计算水平取得了可喜的成绩但在算法水平和执行水平就不如某些联结主义模型有优势(Mcclelland&Thompson,2007;Mcclellandetal.,2010),贝叶斯模型需要解释被试如何表征复杂的问题情境,问题解决过程中大脑神经细胞如何活动等问题:如贝叶斯模型认为被试的推断过程与贝叶斯规则相似,被试首先具备先验知识,然后遇到实验数据,再次结合先验知识和实验数据得到后验知识,那么这些过程是如何在大脑中实现的?先验知识是如何获得并在大脑中表征的?后验知识如何获得等问题都需要一一解释(Griffithsetal.,2010)。
6.3需要扩大模型的解释范围
从模型的功效来看贝叶斯模型是规范性模型,主要解释被试应该如何推断;与其相对的描述性模型主要解释被试实际如何推断。由于先验分布和似然函数的限制,每个贝叶斯模型只能规定一个特定情境中被试应该如何作答,这就极大地限制了所建立模型的解释范围。由于实际的实验情境和影响因素的多样性,研究者几乎必须为每一个实验数据建立一个足够复杂的贝叶斯模型才能保证模型预测的精度,如Support模型涉及三个参数,SS模型涉及四个参数,但都只能解释小范围的因果推理现象,这与科学理论要求的节约原则背道而驰,所以贝叶斯模型必须提高先验分布的抽象水平和似然函数的描述能力,在简化模型形式和提高模型预测能力之间求得平衡,最大限度地提高模型的解释范围。
6.4需要简化计算
如果不是指定先验分布,使用贝叶斯模型计算后验分布的过程太过复杂。本文介绍的几个模型使用蒙特卡洛方法来模拟这个计算过程,当因果图形模型里的原因和效果增加时,计算的复杂程度以几何级数方式增加。解决这个问题依赖于计算理论的发展和相关软件的开发,这就使贝叶斯模型的发展受限于计算理论的发展。但是,即使是有相关的计算理论和软件,要在大量的实验数据的基础上对复杂的因果推理情境(如多原因交互作用等)进行精确的预测也是十分困难的(Perforsetal.,2011)。简化计算是所有贝叶斯模型必须面对的问题。
参考文献
陈希孺.(1999).高等数理统计学.安徽:中国科学技术大学出版社.
韦来生.(2008).数理统计.北京:科学出版社.
Abbott,J.T.,& Griffiths,T.L.(2011).Exploringtheinfluenceofparticlefilterparametersonordereffectsincausallearning.Proceedings of the 33rd Annual Conference of the Cognitive Science Society.
Anderson,J.R.,& Sheu,C.F.(1995).Causal inferences as perceptual judgments.Memory&Cognition,23,510-524.
Cheng,P.(1997).From covariation to causation:A causal power theory.PsychologicalReview,104,367-405.
Chater,N.,Tenenbaum,J.B.,& Yuille,A.(2006).Probabilistic models of cognition:Conceptual foundations.TrendsinCognitiveSciences,10,287-291.
Danks,D.,Griffiths,T.L.,& Tenenbaum,J.B.(2003).Dynamical causal learning.In S.Becker,S.Thrun,& K.Obermayer(Eds.),Advancesneuralinformationprocessingsystems(pp.67-74).Cambridge,MA:MIT Press.
Griffiths,T.L.,Chater,N.,Kemp,C.,Perfors,A.,& Tenenbaum,J.B.(2010).Probabilistic models of cognition:Exploring representations and inductive biases.TrendsinCognitiveSciences,14,357-364.
Griffiths,T.L.,Kemp,C.,& Tenenbaum,J.B.(2008).Bayesian models of cognition.In R.Sun(Ed.),TheCambridgeHandbookofComputationalPsychology(pp.59-100).Cambridge University Press.
Griffiths,T.L.,& Tenenbaum,J.B.(2005).Structure and strength in causal induction.CognitivePsychology,51,334-384.
Griffiths,T.L.,& Tenenbaum,J.B.(2009).Theory-based causal induction.PsychologicalReview,116,661-716.
Kemp,C.,Perfors,A.,& Tenenbaum,J.B.(2007).Learning overhypothesis with hierarchical Bayesian models.DevelopmentalScience,10,307-321.
Lu,H.,Yuille,A.,Liljeholm,M.,Cheng,P.W.,& Holyoak,K.J.(2008).Bayesian generic priors for causal learning.PsychologicalReview,115,955-984.
Lu,H.,Yuille,A.L.,Liljeholm,M.,Cheng,P.W.,& Holyoak,K.J.(2007).Bayesian models of judgments of causal strength:A comparison.In D.S.McNamara & G.Trafton(Eds.),ProceedingsoftheTwenty-NinthAnnualConferenceoftheCognitiveScienceSociety(pp.1241-1246).
Marr,D.(1982).Vision.San Francisco:Freeman.
McClelland,J.L.,& Thompson,R.M.(2007).Using domain-general principles to explain children’s causal reasoning abilities.DevelopmentalScience,10,333-356.
McClelland,J.L.,Botvinick,M.M.,Noelle,D.C.,Plaut,D.C.,Rogers,T.T.,Seidenberg,M.S.,& Smith,L.B.(2010).Letting structure emerge:Connectionist and dynamical systems approaches to cognition.TrendsinCognitiveSciences,14,348-356.
Pearl,J.(2000).Causality:Models,reasoningandinference.Cambridge,UK:Cambridge University Press.
Perales,J.C.,& Shanks,D.R.(2007).Models of covariation-based causal judgment:A review and synthesis.PsychonomicBulletiin&Review,14,577-596.
Perfors,A.,Tenenbaum,J.B.,Griffiths,T.L.,& Xu,F.(2011).A tutorial introduction to Bayesian models of cognitive development.Cognition,120,302-321.
Steyvers,M.,Tenenbaum,J.B.,Wagenmakers,E.J.,& Blum,B.(2003).Inferring causal networks from observations and interventions.CognitiveScience,27,453-489.
Tenenbaum,J.B.,Kemp,C.,& Griffiths,T.L.(2006).Theory-based Bayesian models of inductive learning and reasoning.TrendsinCognitiveSciences,10,309-318.
Yuille,A.,& Lu,H.(2008).The noisy-logical and its application to causal inference.AdvancesinNeuralInformationProcessingSystems,20,1673-1680.
Yeung,S.,& Griffiths,T.L.(2011).Estimatinghumanpriorsoncausalstrength.Proceedings of the 33rd Annual Conference of the Cognitive Science Society.
A Review of the Bayesian Models of Causal Strength Inference
Liu Yanling1,Huang Renhui2,Hu Zhujing3
(1.Education College,Jiangxi Science and Technology Normal University,Nanchang 330013;
2.Mental Health Education Center,Yichun University,Yichun 336000;
3.Psychology College,Key Laboratory of Psychology and Cognition Science,Jiangxi Normal University,Nanchang 330022)
Abstract:On the basis of the essence of Bayesian statistics and the progress of computational technology,Bayesian models of causal strength inference have got rapid development in the last two decades.These models draw post distribute out of the combination of prior distribute and observationdata,and then are used to make prediction based on the post distribute.Different models comprise various prior distribute(assign,uniform,sparse and strong,experiment,et al),likelihood function(Noisy-Or,Noisy-AND-NOT,Noisy-Logical et al),and methods that are used to make prediction(compare different post distribute,compute mean value of post distribute et al).The advantages of Bayesian models include representing the impact of uncertainty by integrating the bottom-up and top-down approach,having a great insight into human participants reasoning process,and playing better to predict participants’ performance than other models.These models need to improve on how to choose appropriate prior distribute,how to explain participants’ various operation on different conditions,and how to decrease computational intractability.The present paper is a brief introduction of Bayesian model’s theoretical basis,mathematical compositions and practical application in causal strength inference.
Key words:causal strength inference;Bayesian model;prior distribute;review
中图分类号:B842.5
文献标识码:A
文章编号:1003-5184(2015)05-0418-07
通讯作者:胡竹菁,E-mail:huzjing@jxnu.edu.cn。
基金项目:*江西省教育科学十二五规划重点课题(14ZD3L017),江西省社会科学规划项目(12JY08),国家自然科学基金项目(31460252)。

