一个随机利率下的家庭型联合保险随机模型
刘文斌, 金艳, 姜今锡
( 延边大学理学院 数学系, 吉林 延吉 133002 )
一个随机利率下的家庭型联合保险随机模型
刘文斌,金艳,姜今锡*
( 延边大学理学院 数学系, 吉林 延吉 133002 )
摘要:通过原点反射Brownian运动过程和Poisson过程对保险实务中的利息力随机性作了描述,在此基础上建立了一类由终身寿险、养老保险和储蓄还本3部分组成的可调整保险金额的家庭型联合保险随机模型,并给出了这类保险模型的年均衡保费的一般计算公式和死亡均匀分布(UDD)假设之下较简洁的年均衡保费计算公式,并用实例分析验证了本文结论的合理性和实用性.本文给出的保险模型对解决寿险公司合理收取保费、保险赔付和规避管理风险都具有一定的理论意义和实际应用价值. 随机利率; 利息力函数; 联合保险随机模型; 年均衡保费 O211.9
文献标识码:A
0引言
随着我国利率市场化改革进程的不断推进以及利率波动频繁等原因,我国寿险公司的产品定价策略的理论和实践面临着新的问题.这是因为,经典的精算理论为了使计算简单,通常假定利率是固定不变的,即寿险保单的预定利率一旦确定,在其生命周期内是不能变化的.利率的变化会造成寿险保单的预定利率和实际利率的偏高,对寿险公司产生重大的影响,因此随机利率下的寿险精算理论与方法的研究成为近年来的热点问题.
1971年,J.H.Polland把利息力作为一个随机变量,对精算函数进行了研究[1],随后很多学者开始考虑寿险与年金中死亡率和利率均视为随机的寿险模型.文献[2-3]采用时间序列的方法对随机利率进行建模,例如白噪声过程、AR(2)过程和ARIMA过程等;文献[4-7]分别得到了利息力由O-U过程和Wiener过程建模的某些年金现值的前二阶矩模型及终身寿险精算现值的前二阶矩等;杨静平等[8]对利息力采用白噪声建模,得到了定期寿险中索赔量极限分布的密度函数递推公式;王明姬等[9]对利息力采用伽马分布和负二项分布联合建立了综合人寿保险模型,并给出了保费缴纳和保险金给付的精算现值;郭春增等[10]采用反射布朗运动过程和伽马分布联合建立了利息力累积模型,并研究得出在此模型下的寿险纯保费和责任准备金的表达式.
随着寿险精算理论研究的不断深入,越来越多的学者致力于研究随机利率下的联合寿险模型.如:王丽燕等对利息力采用Wiener过程建模,构建了家庭联合保险的精算模型[11];王丽燕等对利息力采用反射Brownian运动过程和Poisson过程联合建立了生死两全保险模型,得到了保单全部价值的计算公式,并进一步在死亡力均匀分布假设下简化了公式[12];柳扬等对利息力采用反射Brownian运动过程和Poisson过程联合建立了生死两全保险模型,给出了净保费的一般表达式以及在死亡均匀分布假设下均衡纯保费的简洁计算公式[13].
本文建立一类由终身寿险、养老保险和储蓄还本组成的可调整保险金额的家庭型联合保险双随机模型,考虑到实际生活中的随机利率是由连续的部分和跳跃两部分组成[14],因此本文采用反射Brownian运动过程和Poisson过程来刻画保险中利息力的随机性,并给出年均衡保费的一般计算公式和死亡均匀分布假设下较简洁的表达式.最后利用实例分析验证本文模型的合理性与有效性.
1模型描述与预备定理
1.1 承保对象与保险责任

本文所研究的寿险模型兼顾现代年轻子女的养老负担,因而考虑父母正常的寿险保障外,还增加了还本部分.故在保单中寿险公司的保险责任由如下3个部分组成:
1)寿险部分.采用联合生存状态模式下的即刻给付终身寿险模型,即从保单生效之日起若夫妻双方中任何一人死亡,则寿险公司应向投保人即刻给付保险金A(1+α[T(xy)]), 以此结束寿险公司对投保人的寿险责任部分,其中A为正常数, α为增额系数, [T(xy)]表示T(xy)的取整函数,即(xy)的整数年龄.
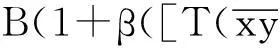
3)储蓄还本部分.采用最后生存者状态下的即刻给付终身寿险模型,即从保单生效之日起若夫妻双方均死亡,则寿险公司应向投保人的委托人(例如子女)退还所缴保费的C倍,其中C为正常数.
1.2 利率的随机化
为更好地刻画利率的随机性,本文采用利用原点反射Brownian运动过程和Poisson过程建立的利息力累计函数模型[12],即
(1)


证明由g(t)的定义可知:
g(t)=E(exp{-y(t)});
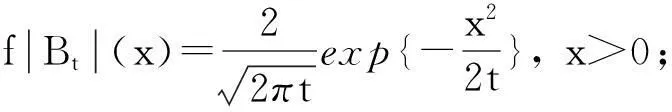
(2)
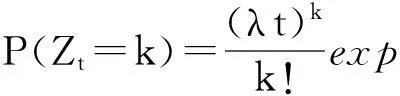
(3)
由式(2)有
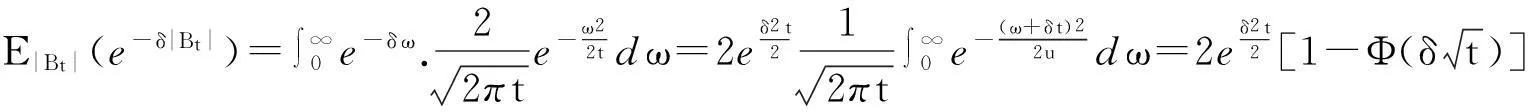
(4)
由式(3)有
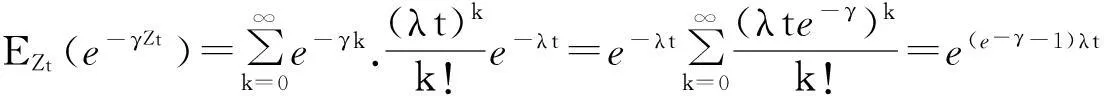
(5)
再由式(1)、(4)和(5)有
g(t)=E(exp{-y(t)})=e-δ tE|Bt|(e-δ|Bt|)EZt(e-γZt)=
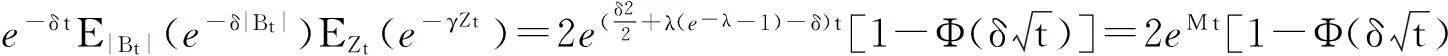
1.3 预备定理及其证明
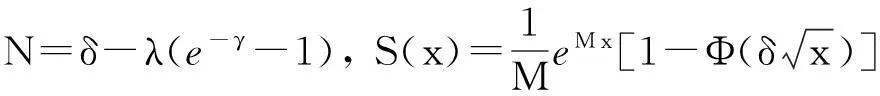
Γk=S(k+1)-S(k),
(6)
证明由Γk和S(x)的定义可知:

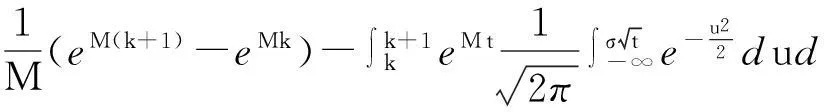
(7)

(8)
其中第1个积分项为
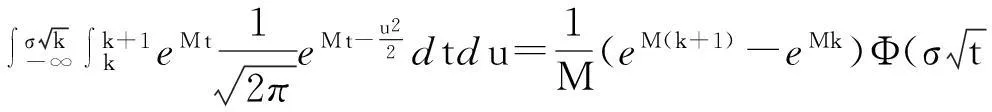
(9)
类似地可得到第2个积分项为
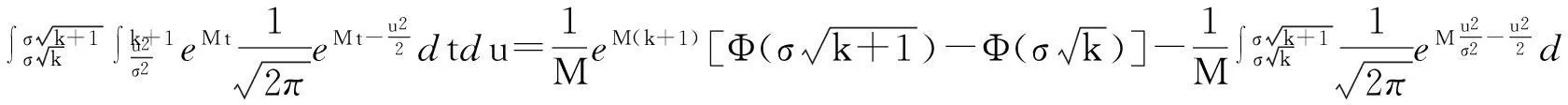
(10)
根据M和N的定义,式(10)中的第2个积分项可改写成
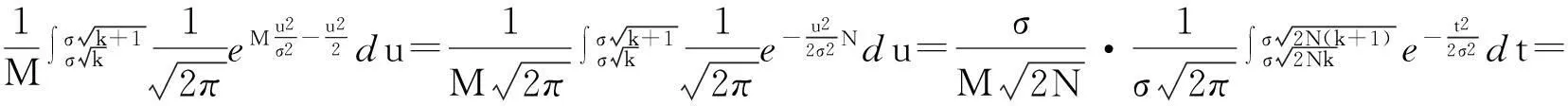
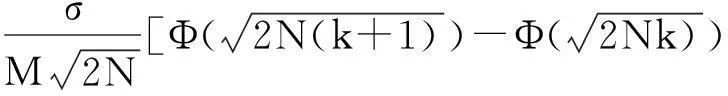
把上式结果代入到式(10),可得

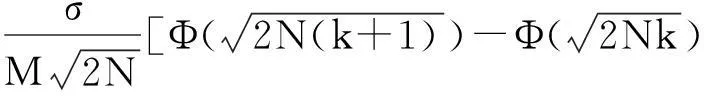
把上式结果和式(9)代入到式(8)可得
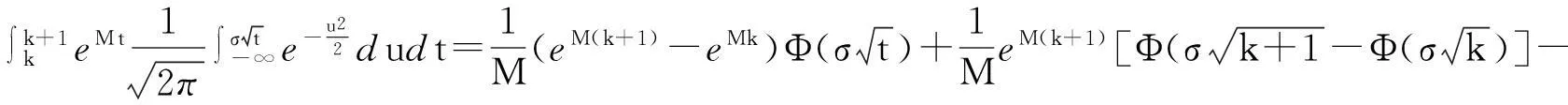
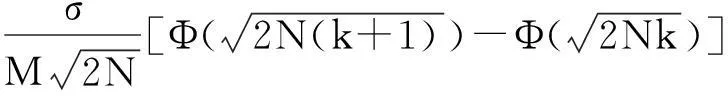
把此结果代入到式(7),便可得到式(6).证毕.
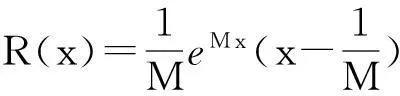
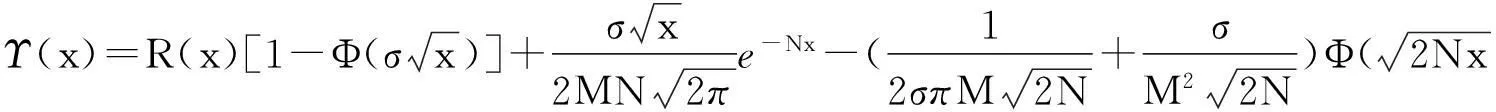
证明类似于定理1的证明过程,经过适当的积分区域分割和积分次序交换后,即可得到结论,由于篇幅所限,故省略证明过程.
2年均衡保费的计算公式
2.1 保单各部分精算现值的计算公式
根据保单责任分别计算保单部分的价值:
1)由于寿险部分的现值Wl可表示为
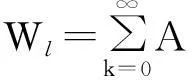
(11)
因此其精算现值为
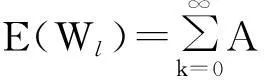
(12)
2)由于年金部分的现值Wa可表示为
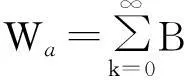
(13)
因此其精算现值为
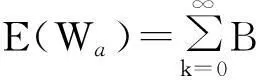
(14)
3)由于储蓄还本部分的现值Ws可表示为
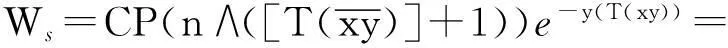
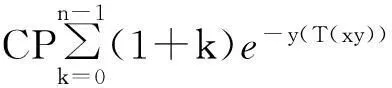
(15)
因此其精算现值为
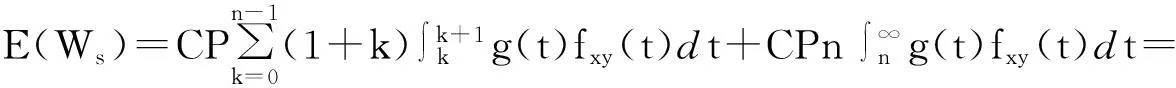
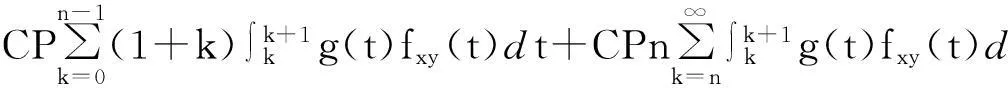
(16)
2.2 年均衡保费的计算公式
综合各部分现值的计算结果可知,寿险公司所要支付的保险金的精算现值为
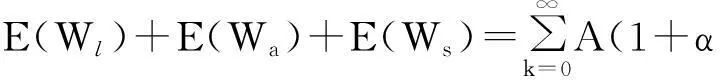
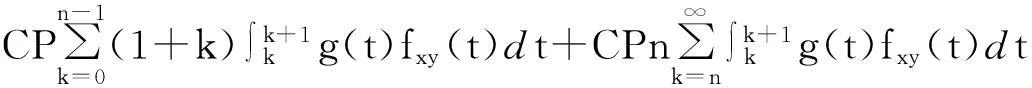
(17)
而投保人所交趸缴净保费的现值Wp可表示为
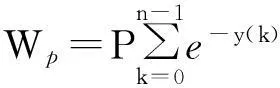
(18)
因此投保人所交净保费的精算现值为
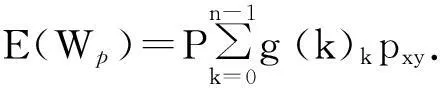
(19)
根据平衡准则可知E(Wl)+E(Wa)+E(Ws)=E(Wp), 解得这类保险的年均衡保费的一般计算公式为

(20)
而在UDD假设下,有:

2(qx+qy)Γk-4qxqyΩk,
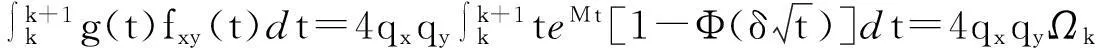
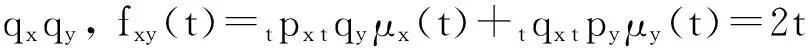
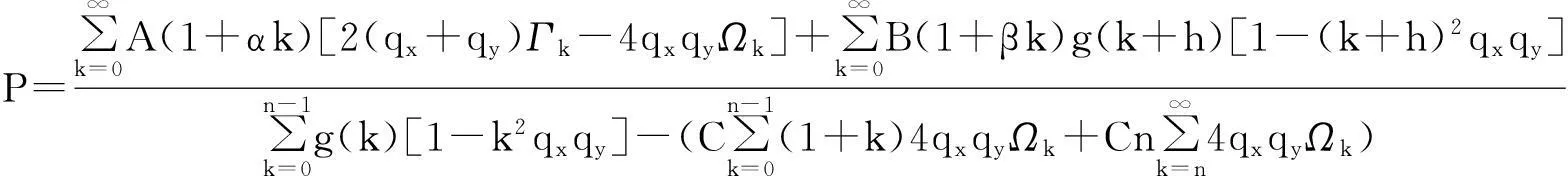
(21)
若生命表中的极限年龄已确定,则当k→∞时,上式中的各项都各自收敛于某一个确定的常数;因此,此式可以通过查表或简单的算数运算就可以得到误差极小的值,其中误差来自Ωk的计算.
3实例分析
假若一对夫妻在年龄分别为x=25岁和y=23岁时投n=25年期的本文所述的保险产品,假设人类极限年龄为M=105岁,国家法定的退休年龄为R=65岁,本试验中累积利息力采用式(1),其中δ=0.02, σ=0.03, γ=0.05,泊松过程Zt的强度λ=0.1.在这类参数假设下,平均利率大致为-ln(g(1))=4.87%.同时,保险的各个参数分别为: A=100 000, B=2 000×12=24 000, C=1, α=0.05, β=0.01, n=25, 则h=R-max(x,y).根据中国人寿保险业经验生命表(CLM03 &CLF03)可知: qx=0.660×10-3, qy=0.285×10-3.
若假定这对夫妻的分数年龄满足死亡均匀分布的假设(UDD),则根据式(21)计算得到的年均衡保费为13 276.998.为了比较投保人和寿险公司的所得,假设T(x)=(1,2,…,M-x), T(y)=(1,2,…,M-y), 此时,在各个年龄组合上本文所述保险产品的寿险部分、年金部分以及还本部分的折现价值如表1—表3所示.所以3个部分的和即为这对夫妻所得到的资金,其在各年龄组合上的折现现值如表4所示.
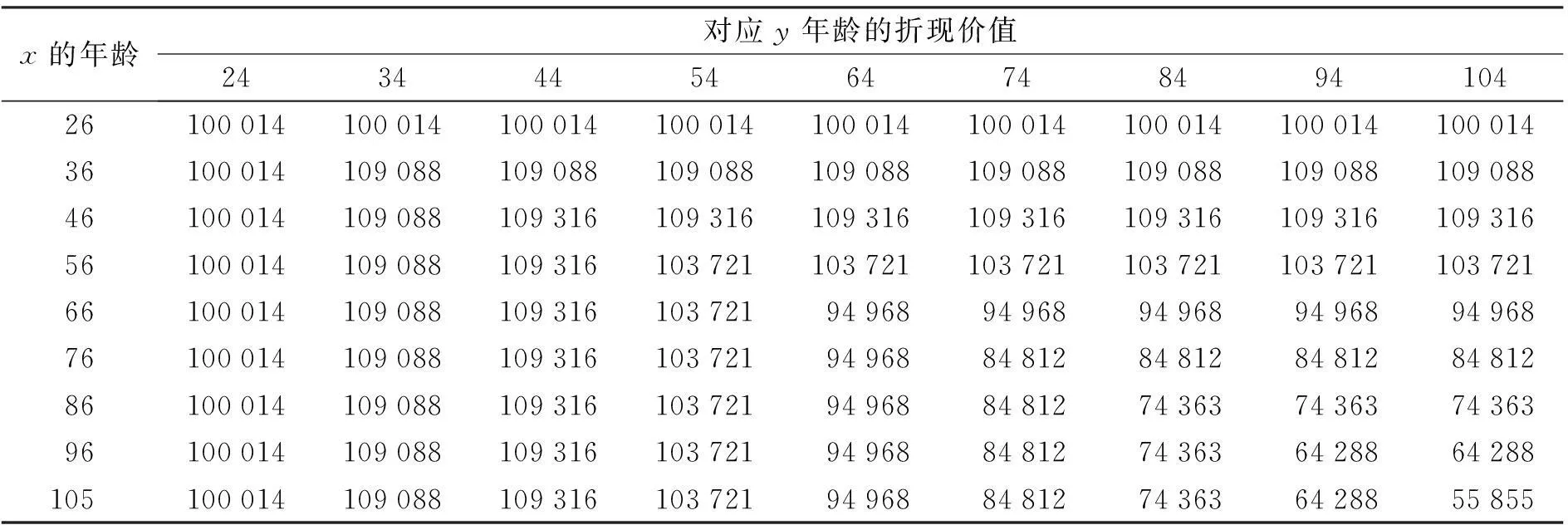
表1 寿险部分的折现价值
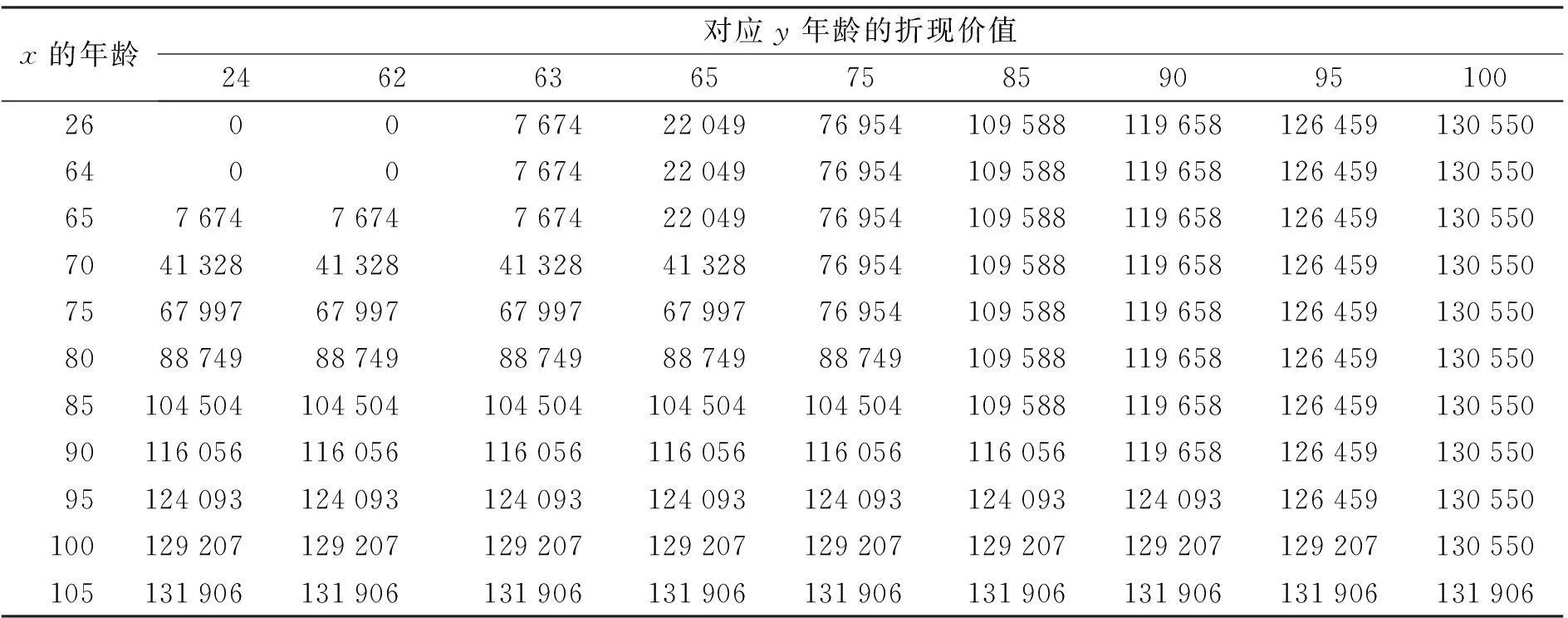
表2 年金部分的折现价值
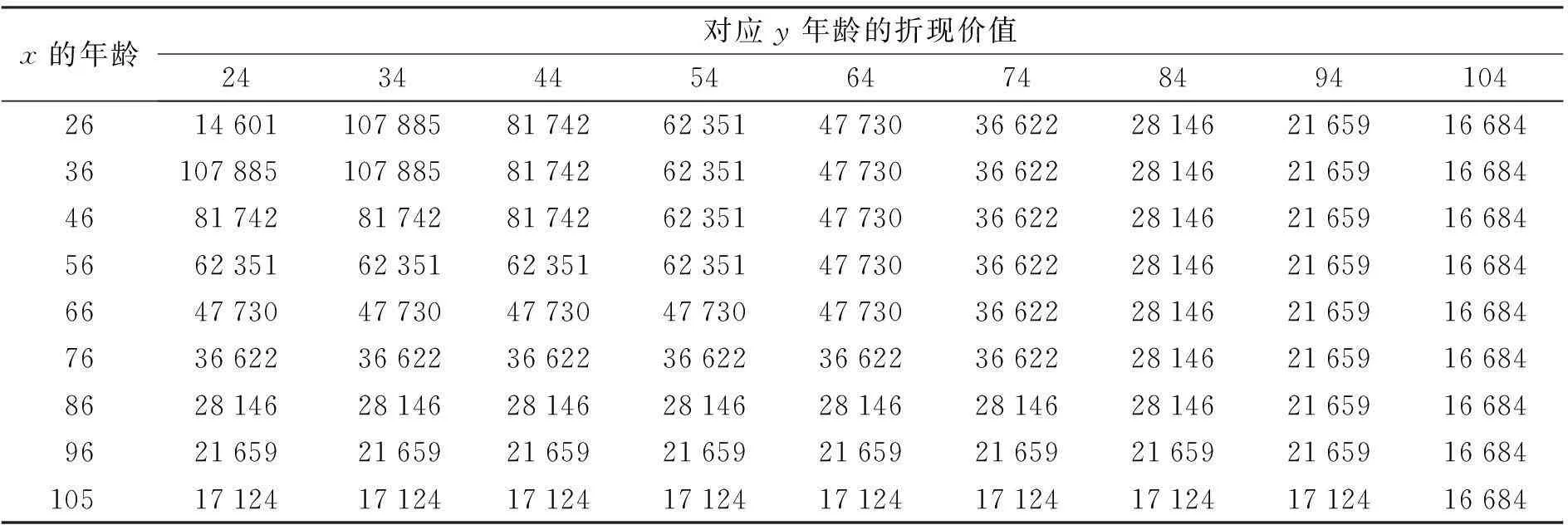
表3 还本部分的折现价值
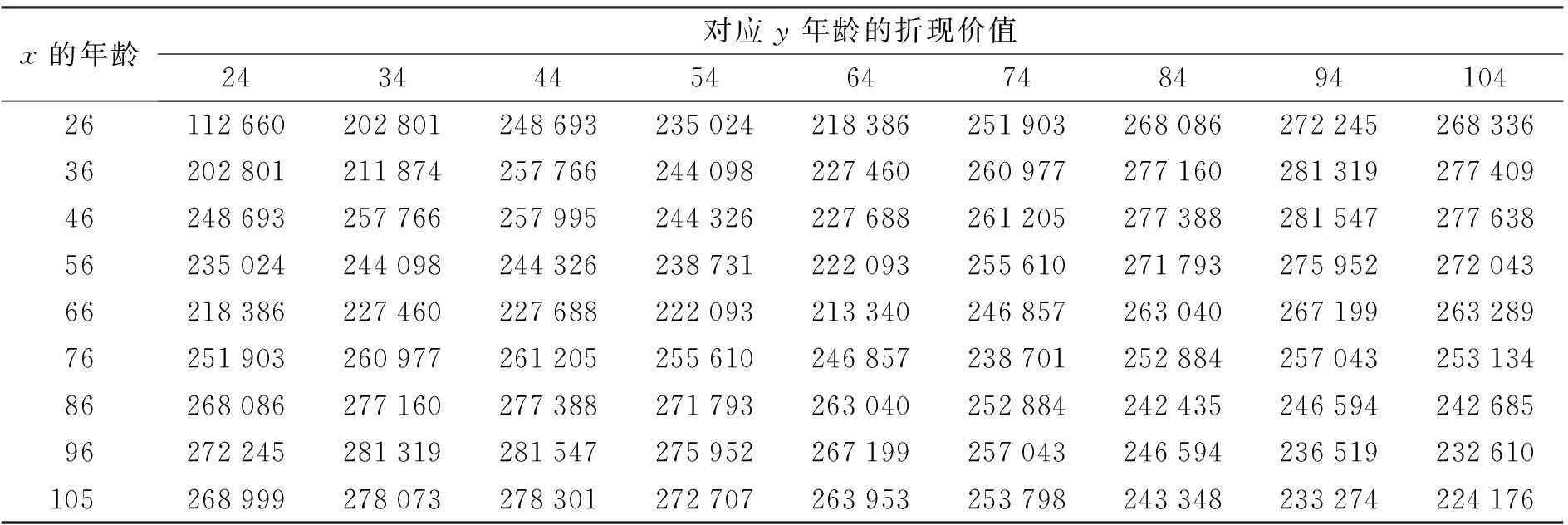
表4 夫妻所得资金的折现价值
参考文献:
[1]Pollard J H. On fluctuating interest rates[J]. Bulletin de 1’Association des Actuaries Belges, 1971,66:68-97.
[2]Dhaene J. Stochastic interest rates and auto regressive integrated moving average processes[J]. ASTIN Bulletin, 1989,19(1):131-138.
[3]Gary Parker. Moments of the present value of the future of a portfolio of policies[J]. Scandinavia Actuarial Journal, 1994,1:53-67.
[4]Beekman J A, Fuelling C P. Extra randomness in some annuities in certain annuity models and mortality randomness in some annuities[J]. Insurance: Mathematics and Economics, 1991,10:275-287.
[5]Beekman J A, Fuelling C P. One approach to dual randomness in life insurance[J]. Scandinavian Actuarial Journal, 1993,76(2):173-182.
[6]Pesand, Skinner. Duration for bonds with default risk[J]. Journal of Banking and Finance, 1974,21(4):1-16.
[7]Hoedemakers T, Beirlant J, Goovaerts M J, et al. On the distribution of discounted loss reserves using generalized linear models[J]. Scand Actuarial Journal, 2005(1):25-45.
[8]Yang J P, Wu L. On the limit distribution ofn-year term life insurance[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 1997,33(5):561-566.
[9]王明姬,田乃硕.息力函数综合寿险模型[J].运筹与管理,2003,13(1):5-8.
[10]郭春增,王秀瑜.随机利率下的寿险精算模型[J].统计与决策,2008,9:53-55.
[11]王丽燕,冯恩民.一种家庭联合保险的双随机模型[J].工程数学学报,2003,20(8):69-72.
[12]王丽燕,郝亚丽,张海娇,等.随机利率下增额两全保险[J].大连理工大学学报,2010,50(5):827-830.
[13]柳扬,洪宇,王丽燕.一个随机利率下的夫妻综合保险模型[J].辽宁师范大学学报(自然科学版),2014,37(4):461-468.
[14]Gary Parker. Limiting distribution of the present value of a portfolio[J]. ASTIN Bulletin, 1994,24(1):47-60.
A home-based combined insurance stochastic model under random interest rates
LIU Wenbin,JIN Yan,JIANG Jinxi*
(DepartmentofMathematics,CollegeofScience,YanbianUniversity,Yanji133002,China)
Abstract:In this paper, first of all, the randomness of the interest force in insurance business is described by both reflex-origin Brownian motion and Poisson process. Secondly, on this basis, we establish a class of adjustable insurance amount home-based combined insurance double stochastic model by whole life insurance, pension insurance and savings payback part, and a general formula of yearly balanced insurance premiums in this type of insurance and a relatively simple formula of yearly balanced insurance premiums with uniform distribution death (UDD) hypothesis are given. Finally, the rationality and practicality for the conclusions are verified by some examples of the analysis process. Type of this insurance model is consistent with the actual situation, and it has important theoretical and practical value for insurance company to charge a reasonable premium, pay insurance and avoid the manage risk.
Key words:stochastic interest rate; interest force function; combined insurance double stochastic model; years balanced premium
文章编号:1004-4353(2015)04-0285-07
*通信作者:姜今锡(1959—),男,博士,教授,研究方向为概率统计、最优化理论.
收稿日期:2015-10-26

